三体船波浪诱导载荷计算研究

1 引 言

三体船是不同于常规高速排水型单体船的新兴船型。由于该船型应用于舰船具有诸多的优点，近几年来，国内外掀起了三体船开发研究的热潮。

英国曾经采用三维脉动源、三维移动动源、三维脉动源与水弹性理论结合等三种理论模型对高速三体船在波浪中的运动与波浪载荷进行了理论研究[1]。

三体船的船体相对单体排水型船来说更加瘦削细长，在高海情时，纵向弯矩和剪力、扭矩依然是结构强度校核时的核心问题[2]。本文基于三维势流理论[3，4]，应用三维时域的方法分析探索了三体船在波浪中航行时的运动与载荷，并最终将时域结果转化为频域，对三体船的典型剖面力进行分析计算。

2 波浪载荷研究理论

2.1 船舶在规则波中的运动与载荷分析计算

在规则波中船体运动与载荷计算广泛应用三维源汇理论，其基本假定为[5]：

1) 船体运动及波浪均是微幅、线性的；

2) 视水为无粘性流体，且为不可压缩的理想流体，其表面张力效应可忽略不计；

3) 运动是无旋的，考虑绕射和辐射的影响。

于是可得到船体在规则波中的运动方程为

[-ω2(M+A(ω))+iω(B(ω)p+Bν)+C+Ce]

X(ω,β)=F(ω,β)

(1)

式中，M为船舶广义质量矩阵，X(ω,β)为单位规则波，ω为波浪圆频率，β为浪向角，A(ω)为附加质量阵，Ce为外部回复力阵，C为静水回复力阵，B(ω)p为势流阻尼阵，Bν为线性粘性阻尼。

2.2 波浪载荷的短期及长期预报基本理论

一般情况下海面上的波浪不会是规则波，它通常呈现为随机的不规则波，所以应采用概率和随机理论的方法来计算波浪诱导船体运动及载荷。

波浪诱导船体运动与载荷的短期和长期预报是建立在以下3个基本假设之上的[6,7]：

1) 认为波浪和船体运动是各态历经的平稳随机过程；

2) 将船舶视为时间恒定的线性系统；

3) 将风浪谱和船舶响应谱视为窄带谱。

2.2.1系统的传递函数

传递函数可以理解为船体在单位波幅的简谐波作用下的船体响应。船体响应包括船体在6个自由度上的运动、波浪作用在船体外壳上的波动压力、波浪诱导船体结构弯矩扭矩剪力结构构件和设备由于运动引起的加速度等。在简谐波作用下随时间而变化的响应函数可写为：

R(ω,β,t)=A·Re[|H(ω,β)|·ei(ωt+φ)]

(2)

式中，H(ω,β)为传递函数，H(ω,β)=HRE+iHIM

(3)

2.2.2海浪谱和响应谱

海浪的随机线性模式常将海浪视为由无限多个频率不等、方向不同、振幅变化而相位杂乱的微幅间谐波叠加而成的不规则波系。根据概率论可以证明：这样构成的海浪，其波面位移服从均值为零的正态过程，该过程具有平稳性和各态历经性。由此，海浪通常可用谱密度来表示其随机性[8]。波浪谱密度函数S(ω)是平稳随机过程的频率描述，它表示不规则波浪的能量相对于频率的分布所以又称为能量谱。不规则波谱表示了不规则波内各单元谐波的能量分布情况。常用的波谱有Pierson-Moskowitz单参数波谱(简称P-M谱)、ITTC双参数波谱、Ochi六参数波谱、JON-SWARP波谱等。

P-M 谱是根据在北大西洋实测的约70个充分发展海浪谱归纳出来的。其原始形式是取海面以上19.5 m处的平均风速U19.5作为其参数，S(ω)为波浪谱密度函数。

(4)

由于有义波高为：

(5)

式(4)又可以写成如下形式：

(6)

本文将采用该P-M谱来反映海浪的随机特征。

对于船舶等线性系统，响应谱即波浪载荷的谱密度等于波浪谱密度函数乘以系统的响应振幅算子，即系统传递函数的平方，如下式：

SW(ω)=S(ω)·H2(ω)

(7)

式中，SW(ω)为波浪载荷谱密度，H2(ω)为响应振幅算子(RAO)。

2.2.3短期预报

短期预报的时间范围为半小时到数小时，在此时间内，船舶的装载状态、航速、航向角以及海情都可以认为是固定不变的。其中在短期预报中，波浪幅值及波浪诱导船体运动的幅值、载荷幅值、应力幅值符合Rayleigh分布，对应的概率密度为：

(8)

式中，E为2倍的波浪载荷方差m，即

E=2m(Hs,Tz,V,β)

(9)

由谱密度函数的性质以及式(8)可知方差为:

(10)

2.2.4长期预报

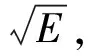
本文采用双参数α和m的Weibull分布来拟合船体运动和载荷的长期响应分布。

(11)

3 实船模型计算和分析

本文基于以上波浪载荷理论，采用三维势流理论和简单格林函数法对三体船的波浪载荷进行分析计算，三体船型主体采用瘦削方尾船型(与英国“海神”号三体船外形类似，无球鼻首)，侧体采用wigley(双向抛物线性数学船型)，主体与侧体船舯的纵向相对位置为15 m。

首先通过对三体船无航速静水状态、静水航行状态分别进行计算，从而可以对三体船进行纵倾平衡调节，同时可以得到三体船的静水载荷，然后计算三体船在波浪中航行的状况。图1为分析三体船波浪载荷时所需的船体三维湿表面和自由液面网格模型：

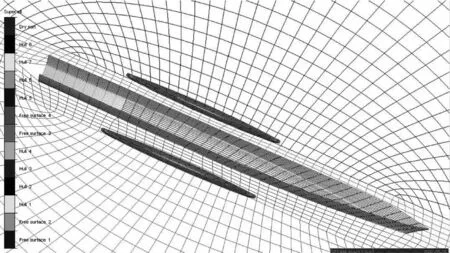
图1 三体船模型

质量模型采用全船纵向质量分布的形式。由于本文主要研究的是三体船总横剖面载荷(垂向剪力、弯矩、扭矩)，因此质量模型可以由沿全船中线面的很多质量点组成，质量点重量各不相同，重心高度不一，这些质量点的总重量重心与全船总重量重心一致，充分反映了三体船全船纵向重量分布的详细情况。全船重量纵向分布如图2所示。

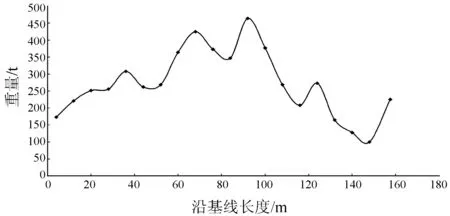
图2 三体船重量纵向分布曲线

计算时的坐标系为X轴指向船首方向，Y轴水平指向左舷，Z轴沿船中心线垂直向上，原点在主体尾柱与基线的交点处。

根据达郎贝尔原理，作用于部分长度船体上的真实流体载荷与刚体惯性力载荷相平衡，于是

(12)

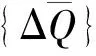
其中船体横剖面内存在剪力和弯矩的封闭条件，即在船首、船尾处，力矩为零。

因此为了准确反映三体船在波浪中的载荷分布特征，沿X轴方向均匀截取了一定数量的剖面(即船体的横剖面)进行分析，表1是所选取的典型横剖面位置。

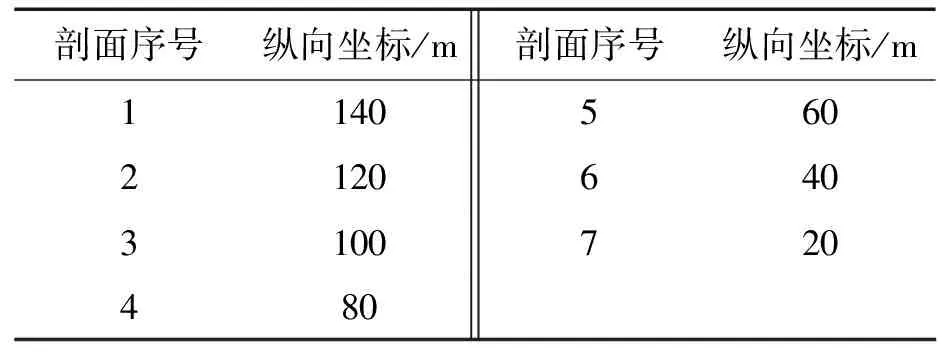
表1 参考剖面位置

由于船体左右舷对称，此处分析的浪向角范围为0°～180°(随浪为0°，顶浪为180°)，以每15°为间隔。按照国际船级社(IACS)建议，选取北大西洋波浪散布图，计算三体船在不同的概率水平(10-2～10-10)时的波浪弯矩、剪力、扭矩的长期预报值。一般来说，剖面力在超越概率为10-8水平时极值相当于重现期为20～25年的遭遇值。

通过对三体船在规则波中传递函数的计算，可以得到规则波中船舶运动响应的频响函数，应用达郎贝尔原理计算三体船典型横剖面内的总垂向剪力、垂向弯矩、扭矩，结合所选海浪环境对三体船波浪载荷进行短期和长期预报。对各个剖面不同浪向角和超越概率水平下的剖面载荷值分别进行预报，经过一定的整理分析，求得各个剖面力极值以及极值发生的浪向角。表2所示为每个剖面波浪载荷长期预报极值的详细情况。

在给定的超越概率为10-10时，分析不同剖面在不同浪向时的垂向剪力和扭矩、垂向弯矩变化趋势和规律。图3～图5分别是其剖面载荷极值走势图。

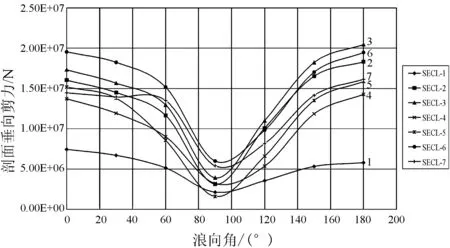
图3 不同浪向角时典型剖面垂向剪力极值图

表2选取剖面的剖面载荷预报极值

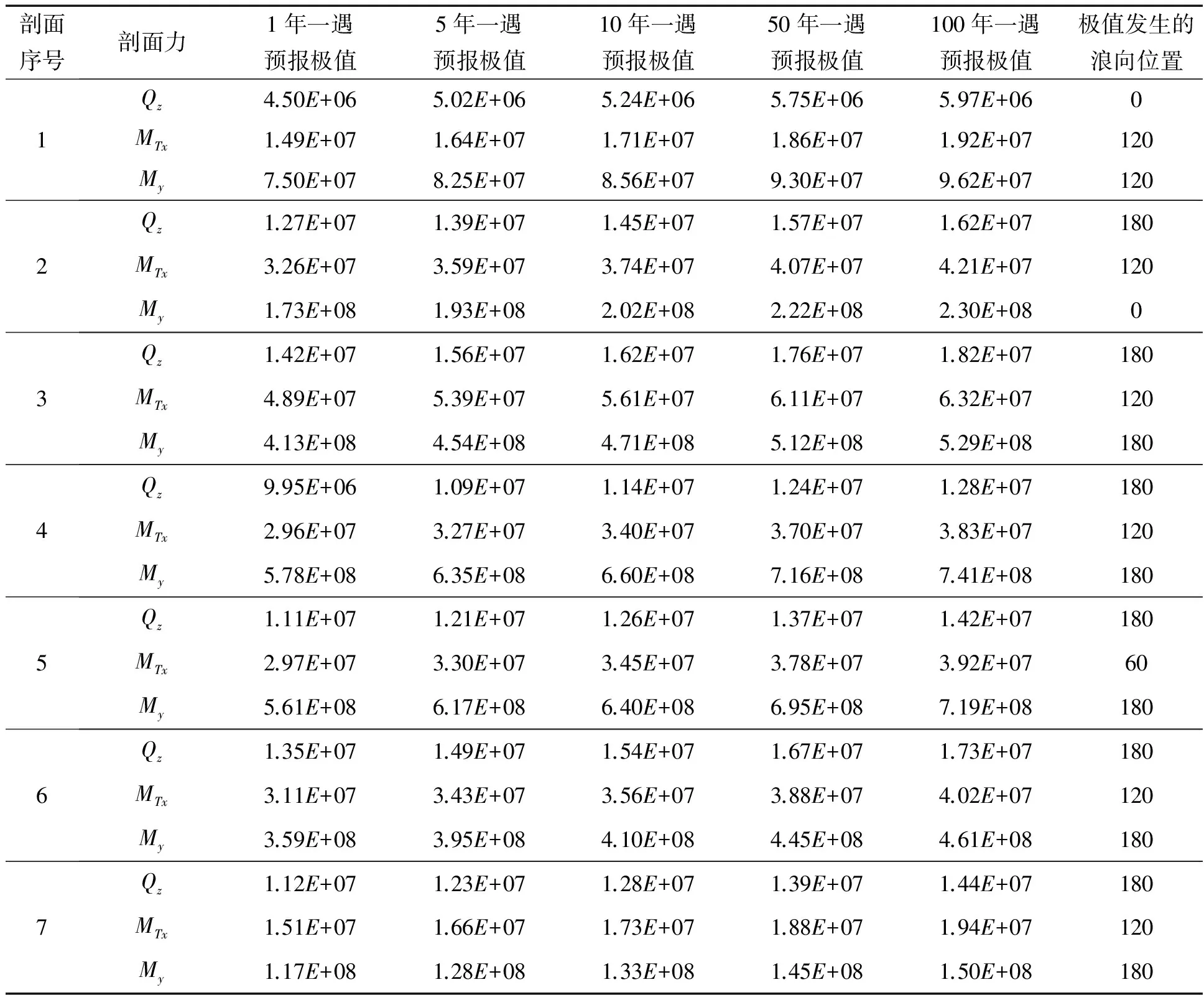
剖面序号剖面力1年一遇预报极值5年一遇预报极值10年一遇预报极值50年一遇预报极值100年一遇预报极值极值发生的浪向位置1Qz4．50E+065．02E+065．24E+065．75E+065．97E+060MTx1．49E+071．64E+071．71E+071．86E+071．92E+07120My7．50E+078．25E+078．56E+079．30E+079．62E+071202Qz1．27E+071．39E+071．45E+071．57E+071．62E+07180MTx3．26E+073．59E+073．74E+074．07E+074．21E+07120My1．73E+081．93E+082．02E+082．22E+082．30E+0803Qz1．42E+071．56E+071．62E+071．76E+071．82E+07180MTx4．89E+075．39E+075．61E+076．11E+076．32E+07120My4．13E+084．54E+084．71E+085．12E+085．29E+081804Qz9．95E+061．09E+071．14E+071．24E+071．28E+07180MTx2．96E+073．27E+073．40E+073．70E+073．83E+07120My5．78E+086．35E+086．60E+087．16E+087．41E+081805Qz1．11E+071．21E+071．26E+071．37E+071．42E+07180MTx2．97E+073．30E+073．45E+073．78E+073．92E+0760My5．61E+086．17E+086．40E+086．95E+087．19E+081806Qz1．35E+071．49E+071．54E+071．67E+071．73E+07180MTx3．11E+073．43E+073．56E+073．88E+074．02E+07120My3．59E+083．95E+084．10E+084．45E+084．61E+081807Qz1．12E+071．23E+071．28E+071．39E+071．44E+07180MTx1．51E+071．66E+071．73E+071．88E+071．94E+07120My1．17E+081．28E+081．33E+081．45E+081．50E+08180

注：表中Qz为垂向剪力(N)，MTx为剖面扭矩(N·m)，My为剖面垂向弯矩(N·m)。

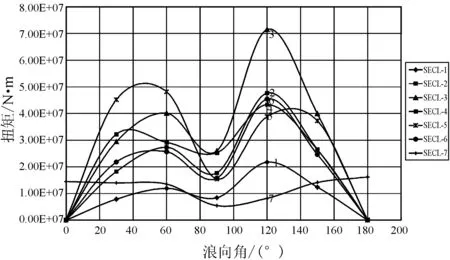
图4 不同浪向角时典型剖面扭矩极值

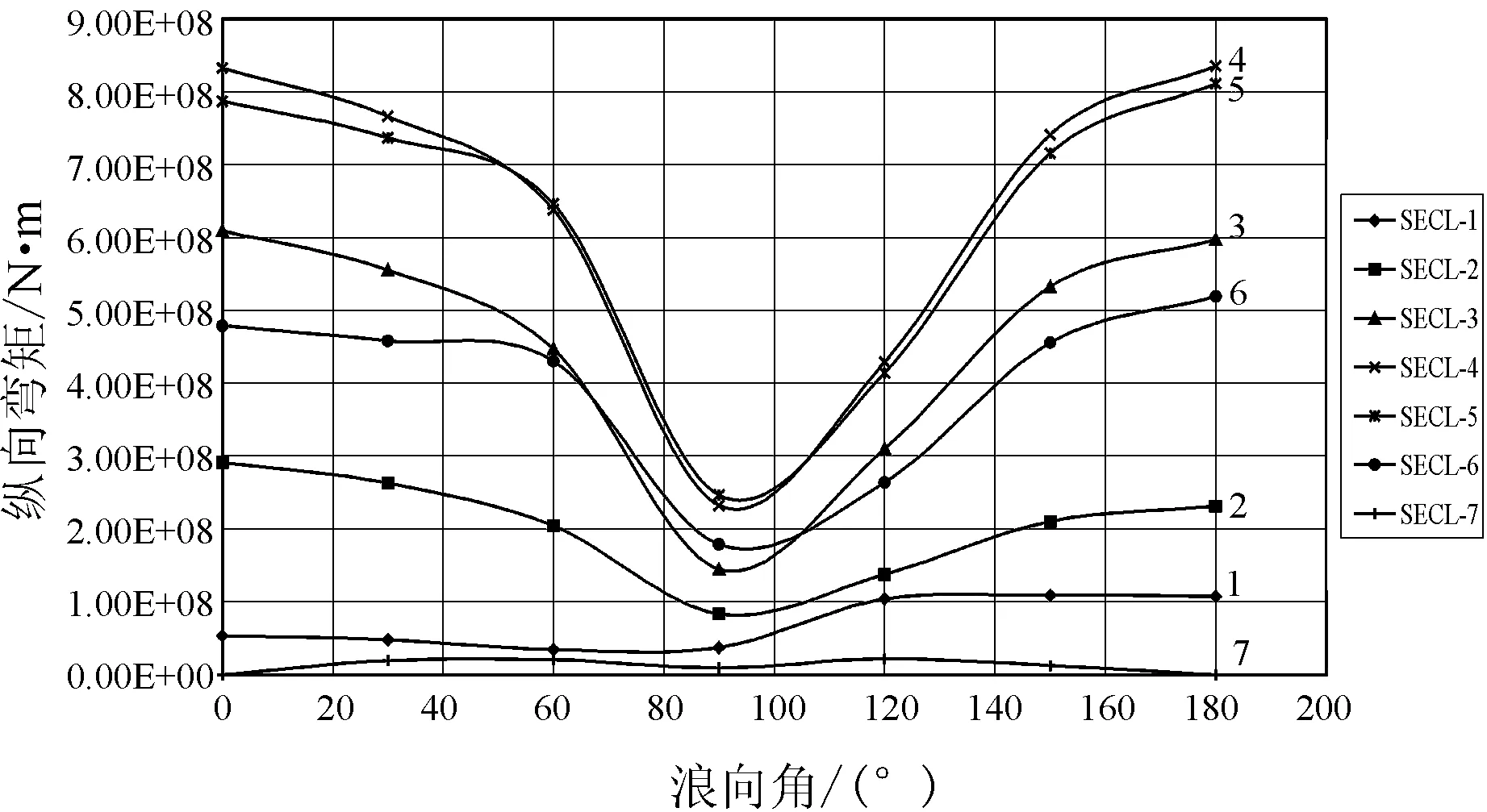
图5 不同浪向角时典型剖面垂向弯矩极值

通过图3～图5不难发现全船剖面载荷具有以下分布规律：

1) 由表2可以发现，选取的三体船1～7个剖面中，最大垂向剪切力发生在三体船3号剖面(X轴纵坐标100 m处)，此时的浪向角为180°。最大扭矩也发生在3号剖面处，此时的三体船与波浪位置为：浪向角120°斜浪状态。最大垂向弯矩发生在4号(船舯)剖面处，此时浪向角为180°。

2) 三体船在波浪中的垂向剪切力随着浪向角变化呈下降再升高趋势，其中浪向角为90°时，剖面总的垂向剪切力最小，在0°和180°时剖面最大。

3) 三体船在波浪中的剖面扭矩出现一定的波动状态，剖面扭矩在浪向角30°～60°范围内出现一个峰值，在120°附近再现一个峰值。其中在0°和180°时剖面扭矩最小，浪向角为90°时，剖面扭矩较小。这是符合扭矩产生的实际原理的。

4) 三体船在波浪中的剖面垂向弯矩随浪向角变化呈先下降再上升趋势，垂向弯矩的极大值发生在浪向角为0°和180°时，其中横浪状态(浪向角为90°时)垂向弯矩最小。距离船舯越近，垂向弯矩越大，而首尾处剖面垂向弯矩最小。

4 结束语

本文通过对三体船波浪载荷的探索性计算分析，初步找到三体船在波浪中运动时剖面载荷的分布规律和趋势。可以发现，三体船在波浪中航行时，其剖面垂向剪力和垂向弯矩一般在顶浪和随浪状态时最大，需要重点考虑此两部分的剖面载荷。其中横浪时，全船垂向弯矩、垂向剪力和扭矩相对来说比较小；斜浪状态时，扭矩比较大。这与常规单体船的剖面载荷分布走势和规律基本一致。距离船舯越近，剖面载荷越大，首尾两端附近载荷均较小。在进行三体船结构强度设计与计算时，应注意不同浪向角时需关心的主要剖面载荷。

参考文献:

[1] 卢晓平，郦云，董祖舜.高速三体船研究综述[J].海军工程大学学报，2005,17(2):43-48,52.

[2] WU Mingkang,HERMUNDSTAD O A.Time-domain simulation of wave-induced nonlinear motions and loads and its applications in ship design[J]. Marine Structures,2002,15(6):561-597.

[3] XU Jinsong, HADDARA M R.Estimation of wave-induced shiphull bending moment from ship motion measurements[J].Marine Structures,2001,14(6):593-610.

[4] IIJIMA K,SHIGEMI T,MIYAKE R,KUMANO A.A practical method for torsional strength assessment of container ship structures[J].Marine Structures,2004,17(5):355-384.

[5] 戴仰山，沈进威，宋竞正.船舶波浪载荷[M].北京：国防工业出版社,2007.

[6] SOARES C G,SCHELLIN T E. Long term distribution of non-linear wave induced vertical bending moment on a containership[J]. Marine Structure, 1996,9(3/4):333-352.

[7] SOARES C G,FONSECA N,PASCOAL R. Long term prediction of non-linear vertical bending moments on a fast monohull[J].Applied Ocean Research,2004,26(6):288-297.

[8] SOARES C G.On the uncertainty in long-term predictions of wave induced loads on ships[J].Marine Structures,1999,12(3):171-182.

[9] PERUNOVIC J V,JENSEN J .Wave loads on ships sailing in restricted water depth[J].Marine Structures,2003,16(6):469-485.

[10] CHAN H S, ATLAR M, INCECIK A.Global wave loads on intact and damaged Ro-Ro ships in regular oblique waves[J].Marine Structures,2003,16(4):323-344.