基于证据理论的货运船舶避碰行为选择模型

梁世翔，刘 杰，沈卫文

（1.武汉理工大学ITS中心，武汉430063；2.武汉交通职业学院，武汉430062）

航行中的船舶在面临碰撞风险时，如何选择避碰行为，减少碰撞风险和损失是船舶驾驶员要考虑的首要问题［1］。避让行为的选择涉及到船舶驾驶员的心理、经验、避让规则制度和外界环境等多种不确定因素的影响，是一种不确定推理。利用证据理论建立货运船舶的避碰模型，能对碰撞行为进行风险评价，为船舶驾驶员选择避碰行为提供决策依据。

1 证据理论及其融合机理

D-S证据理论是由丹普斯特（Dempster）在1967年最初提出，并由他的学生莎弗（Shafer）在1976年改进并推广形成的一种不确定推理模型。该理论引入可信度函数来量度不确定性，引用似然函数来处理由不知道而引起的不确定性。

1.1 可信度函数

为了描述假设的不确定性，D-S证据理论首先引入关于可信度分配函数的概念。设论域Θ为所有可能假设（表示为原子命题的结论）的有限集合，且Θ中的元素间是互斥的，则可以在Θ的幂集2Θ上定义一个可信度分配函数（基本概率分配函数）m∶→［0，1］，满足

其中：A称为焦元；m（A）数值称为基本概率分配函数（基本可信度分配），它表示依据当前环境（证据）对假设集A（Θ的了集）的信任程度［2-4］。

1.2 证据合成

设Bel1和Bel2是同一识别框架Θ上的两个可信度函数，m1、m2分别是其对应的基本可信度分配，焦元分别为A1，A2，…，Ak和B1，B2…，B1，设

定义函数m：2Θ→［0，1］是可信度分配，则：

用式（1）求m1，m2直和的方法称为Dempster合成法则。

应当指出的是，多个证据的融合可由两个证据融合后经递推后得到，因此，在实际求解时，为降低计算的复杂程度，常常通过递推来进行多个证据的合成［5-6］。

1.3 证据决策

设决策系统的状态集为S＝｛x1，x2，…，xq｝，决策集为V＝｛v1，v2，…，vp｝，报酬函数为：

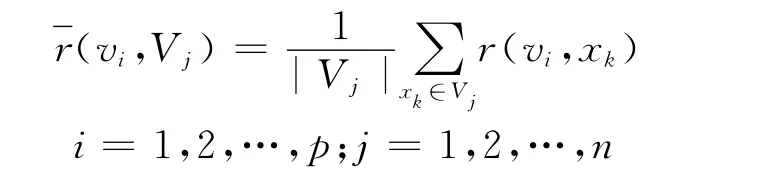
选取目标为：

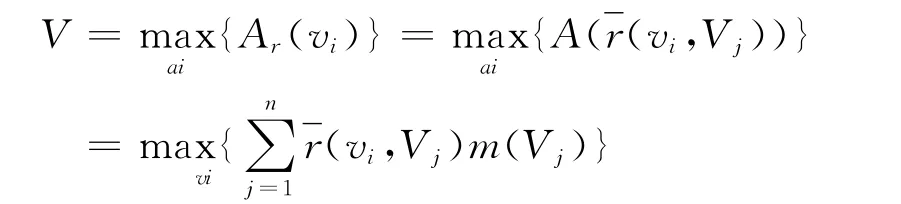
若v＊∈V，使Ar（v＊），则V＊即为最优决策。

当r（vi，xj）失去损失意义时，可先将r（vi，xj）取负值，再利用上述规则计算。

2 船舶避碰方案选择及其实证研究

在船员的避碰知识结构中，避让行动的确定是与决策者的人为因素关系最密切的知识，因人而异，且随会遇局面的不同而不同，没有一个固定的模式。在研究智能避碰专家系统的过程中，必须用定量的方法来研究采取的避碰行动，综合起来，避碰措施可分为以下10种。

1）保向保速；

2）符合大幅度原则的右转；

3）向右转向与他船平行；

4）向右转向把他船置于船尾；

5）大角度向左转向；

6）向左转向与他船平行；

7）向左转向把他船置于船尾；

8）减速；

9）停车；

10）紧急倒车。

在上述行动当中，常规行动有三种：大幅度转向，减速和保向保速。其余为应急行动。由于避碰行为具有不确定性，可利用证据理论和M决策法来优选避碰方案。

2.1 货运船舶避碰方案的选择

影响选择避碰方案的关键指标是代表其碰撞风险度的多项指标，包括避让行为的损失、对风险的反应时间及碰撞风险。在方案的核心碰撞风险指标识别出来后，可依据下列条件来选择避让行为。e（i），（i＝1，2，…，n）表示知识库中尚有i个候选方案作为目标方案入围，则满足下列条件的避让行为即为我们所选的避让行为。

1）避让损失C最小。避让损失C主要包括因避让行为失败所带来的损失；

2）驾驶员对碰撞风险的反应时间。船舶驾驶员为更快地把握快速变化的碰撞风险，要求驾驶员对所采取的避让行为下对碰撞风险的反应时间T最短。

3）碰撞风险测度R最小。船舶碰撞风险测度定义为避让行为的碰撞风险因子的期望值与其可能出现的概率的矩阵。

2.2 避让行为选择的实证研究

2.2.1 避让行为状态描述

设一货运船舶在航行中面临碰撞风险，驾驶员为防与目标船发生碰撞，选择避让行为。避让行为集为V＝｛vj｝（i＝1，2，…，n），其模糊集分别为高、中、低，其对应的取值因人而异。船舶驾驶员面临碰撞风险时采取常规避让行为为大幅度转向、减速和保向保速，分别记为V1，V2，V3，每一种避让行为失败所带来的风险损失不同，避让行为对碰撞的反就时间及避让行为所带来的碰撞风险不同，而且因驾驶员对风险的认识不同取不同的值。设各候选行为的风险成本、对风险的反应时间和碰撞风险测度经测算，分别见表1、2、3。要从上述3个候选行为中，选择最佳的行为作为本船舶所应采取的避让行为。这一决策过程可由证据理论通过证据融合后给出。

表1 候选行为的风险成本

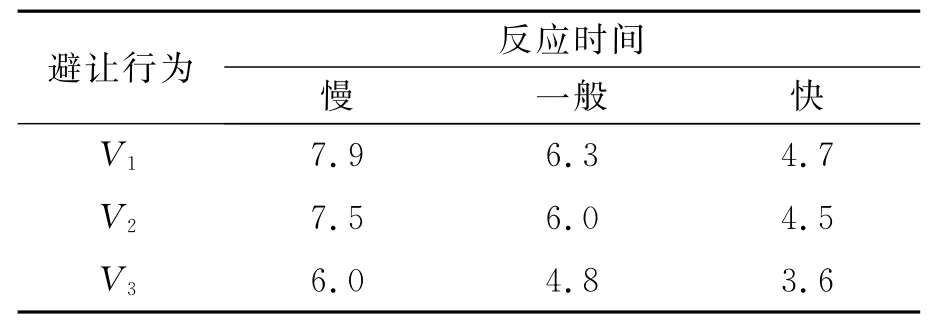
表2 候选行为的碰撞反应时间

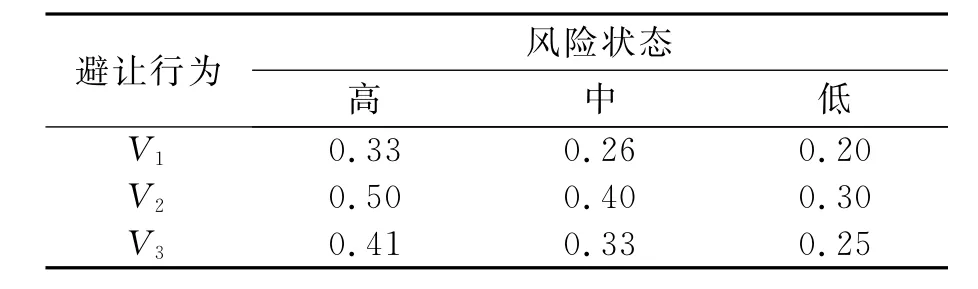
表3 候选行为所带来的碰撞风险测度

2.2.2 避让行为选择

这实际上是一个多目标优化决策的问题，根据信息融合中的证据理论求解如下。

1）单目标决策。根据M决策法，分别对候选行为的风险成本、反应时间、风险测度进行单目标决策，Er（vi）（i＝1，2，3）。求出 Ar（vi）后，将Ar（vi） i＝（1，2，3）进行归一化，把得到的A′r（vi）（i＝1，2，3）当作框架上的基本可信度分配mj（vi）（i＝1，2，3；j＝1，2，3）。

2）证据合成。运用Dempster-Shafer合成法则，对求得的进行mj（vi）（i＝1，2，3；j＝1，2，3）合成，得到m（vi）（i＝1，2，3），于是就可以根据 Max｛m（vi）（i＝1，2，3）｝决定船舶驾驶员的避让行为。

3）选择避让行为。根据M决策法的思想，分别将表1、2、3进行适当变换，具体就是将表中各项分别取倒数，得到表4、5、6，这样就符合关于报酬值的含义了。

表4 候选行为的风险成本取倒数

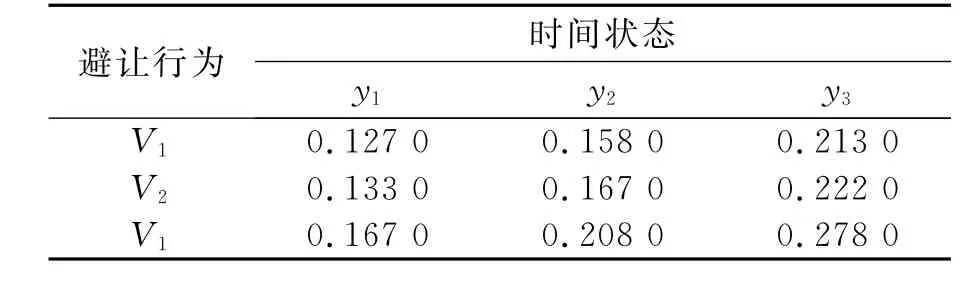
表5 候选行为反应时间取倒数

表6 候选行为风险测度取倒数

由此可见，该问题的识别框架即状态集合S为｛（x1，x2，x3）；（y1，y2，y3）；（z1，z2，z3）｝

经过计算可求得在识别框架上的基本可分配度见表7。

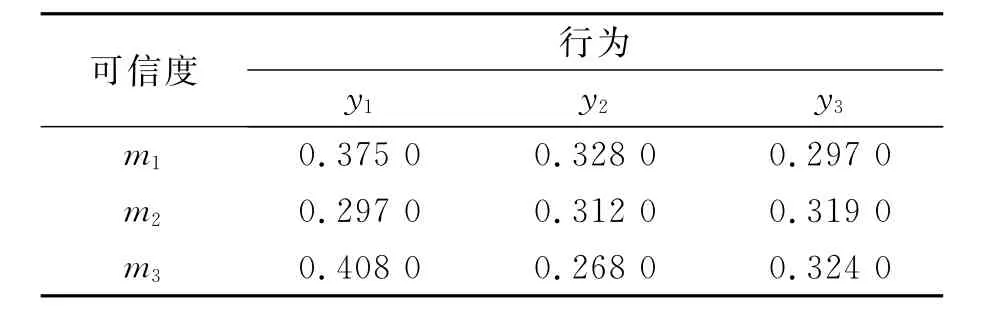
表7 基本可信度分配

根据D-S合成法则，可分别求得三个行为的可信度如下：

根据合成结果，可以得出如下结论：虽然避让行为v3的风险反应慢，但碰撞风险成本低，而且碰撞风险也最小，可作为船舶驾驶员的最佳的避让行为。

3 结论

利用证据理论辅助选择船舶的避让行为具有广泛的应用前景，当需要考虑的参数很多时，由于计算量很大，需要选取合适的算法和可信度分配，有助于提高避让行为选择的可信度。

［1］程细得，刘祖源.船舶智能避碰专家系统研究［J］.武汉理工大学学报：交通工程版，2003，1：93-94.

［2］高 济，朱淼良，何钦铭.人工智能基础［M］.北京：高等教育出版社，2002.

［3］蔡自兴，徐光祐.人工智能及其应用［M］.北京：清华大学出版社，1996.

［4］尹朝庆，尹 皓.人工智能与专家系统［M］.北京：中国水利水电出版社，2001.

［5］安居白.智能信息处理［M］.大连：大连海事大学出版社，2000.

［6］ALP WINCKLE D S，BROOKING M A，HART D K.OPA 901IMO Legislation and the Ship Emergency Response Service［S］.Lloyd's Register of Shipping，1995.