估算教学:价值、策略及评价

【按】“估算”应该算是数学新课程里出现的一个崭新的内容。由此，教师的“陌生感”不言而喻。六七年来，估算教学出现了不少问题。例如，学生一看到“大约”就估算；更习惯于精算而不是估算；教师不知该如何评价估算结果的优劣，等等。这些问题甚至让人怀疑，是否有必要引入这样一个内容？学生学习估算的价值到底在哪里？

本期刊登两篇文章，一篇探讨估算教学中存在的突出问题；另一篇探讨教师在估算方面本体性知识的缺失，希望引起读者的关注。

一、问题的提出。

【案例1】“尴尬”的估算

背景：学生已经有了一定的估算基础，在具体情境中让学生用估算解决问题时，出现了以下两种情况。

情境一：

某校期末考试卷上有这样一道估算题：

每个足球78元，要买2个足球，请你估计150元够吗？

阅卷时发现，学生几乎全是用精算算出结果的，即78×2=156（元），156﹥150，所以不够。

学生这样解答算不算对？给不给分？

對此，教师的意见不一，有人认为，虽然学生采用了精确计算的方法，只要结果是正确的，就应该给予肯定；也有人认为，学生没有认真审题，不能给分。

情境二：

（1）课上通过一个实际问题引入估算。

（2）教师抽象地谈在一个算式中，每个数可以怎么进行估计。

———“388”可以怎么估？

（380，390，400，300）

———在388+120，388+110中，你打算分别怎样估“388”才能做到不仅计算速度快，而且与实际结果相差最小？

生1：388+110中，388估成390，因为10+90=100，结果凑成整百。

师：用这个方法计算的结果是不是最接近实际结果呢？

生1：是，因为390离388最近。

生2：用四舍五入法。

（教师再次强调题目要求：又快又与实际结果相差最小。）

生3：388+120，388估成380最方便，因为相加为整百数。

师：用这种方法计算的结果不是离实际结果最近。388可以估成390。

（3）最后解决一个实际问题：一班学生238人，二班学生158人，399个座位够吗？

学生分6个小组进行讨论后，有5个小组用了前面所强调的“不仅计算速度快，而且与实际结果相差最小”的思路，将238估计为240，158估计为160，240+160=400，所以399个座位不够；有1个小组进行了精确计算，发现399个座位够。面对学生不同的答案，教师说道：“确实，有些问题是不能用估算解决的，必须进行精确计算。”

学生在上完课后，对教师说道：“好像只有在您的课堂中才用到估算。”教师陷入了尴尬中。

对此，部分教师认为：（1）教师面向全体强调“好”的估算标准，这拔高要求了。（2）习题的设计欠妥，学生感受不到估算的价值。

由以上案例，可以引出以下几个问题：

（1）在实际教学中，学生常常习惯于精确计算，而不愿意进行估算，学生为什么会缺乏估算意识？

（2）估算的价值体现在哪些方面？如何培养学生的估算意识？

（3）在情境二中，教师一直强调“好”的估算标准是“不仅计算速度快，而且与实际结果相差最小”，这个标准是否合理？估算是否有“统一”标准？

下面，我们就来讨论这几个问题。

二、估算到底有什么价值？

估算到底有什么价值？这也是许多教师在教学当中不断遭遇的困惑。如果教师都不能深刻地体会到，那么可想而知教学如何能到位。在此我们做一个简单的描述。

1.估算在日常生活中有着广泛的应用。

估算是对运算过程和运算结果进行粗略估计的一种能力。在现实生活中，很多事实际上不可能也不需要都进行准确计算。曾经有一个学者做过一个统计，将一个人在日常生活当中精确计算的机会和粗略估计的机会进行比较发现，后者多得多。例如，我们每个家庭都要计划收入和支出，这就需要估计；一个商场，它的营业额是多少，它的利润如何，要进行大致的预测，这也是估计；再比如，现在大城市流动人口很多，到底流动人口是多少，我们在做统计时也要做一些估计，一般来讲尾数就省略不计了。由此可见，生活中离不开估算。因此，估算作为数学计算教学方面的一个新内容提出来，是有道理的。

2.估算为判断计算器、口算和笔算结果是否合理提供了依据。

估算为判断计算器计算得是否准确，包括孩子们口算、笔算的结果是否合理，提供了重要的依据。小学生开始使用计算器，算出来的结果一般都是准确的，但有时候由于操作失误也可能会出现问题，如果学生有了估算的意识和能力，就能很快发现计算器计算的结果其取值范围是否合理。过去我们要用加减法的互逆关系和乘除法的互逆关系来验算，现在用估算的方法就可以解决了，这也是估算的重要应用。

3.估算有利于人们事先把握运算结果的范围，是发展学生数感的重要途径。

《数学课程标准（实验稿）》在发展学生的数感方面明确指出：能估计运算的结果，并对结果的合理性作出解释。估算是发展学生数感的有效途径之一，也是保证计算正确的重要环节，尤其对提高学生的计算能力很有益处。计算前进行估算，可以估计出大致结果，为计算的准确性创设条件；计算后进行估算，能判断计算有无错误并找出错误的原因，及时纠正。在学生的日常口算和笔算过程中，无论是计算前估算还是计算后估算，都有一定的价值。另外，对培养孩子的快速判断和推理能力也有一定的好处。

4.估算对学生后续的数学学习有重要作用。

总之，作为数学教师，我们只有更加深刻地感受估算在生活、工作中的价值，我们才能在教学中自觉地、适时、适度地培养学生的估算意识和估算能力。

三、估算教学该如何进行？

目前的估算教学，从学生角度来讲，主要存在两个问题：一是学生不知道什么时候用估算，往往一看见有“大约”就开始估了；二是学生不知道在什么情况下选择什么样的估算策略，也就是怎么能够合理地应用估算策略。因此，估算教学必须从以下几个方面入手。

1.培养估算意识。

估算教学，不是单纯地教学生记住一些估算的方法，而是培养学生近似的估算意识，让学生逐步理解估算的意义。在这个过程中，应当多增加学生的体验，不断丰富学生这方面的经验。下面提几条具体的教学建议。

（1）教师要把估算意识的培养作为重要的教学目标。

如果把教学目标定位在今天就教会往大估，或是见到“大约”就要估算，做一些机械的训练，可能会使学生形成一种错误的思维定式。因此，必须把教学目标拉回到培养估算意识上来。这个意识的培养不是一两堂课就能解決的显性目标，需要在每一堂估算课及与估算相关的课堂活动中进行渗透，因而需要教师予以特别的关注。

（2）设计出好问题，让学生体会到估算的必要性。

只有选好题目、提出好问题，学生才能体会到估算的价值和必要性，他的估算意识才能不断增强。这对教师来说，是一个挑战。比如，一家三口去饭馆吃饭，当时点了一些饭菜，价钱分别是42元、56元、19元、33元、25元、9元，当时就大致地估了估，不够200元。服务员收费时却报出了226元。这显然是错误的。经查证，服务员将42元记了两次，多收了42元。正是因为有了估算的意识才避免了服务员的错收费。这就是一个有估算价值的问题。

（3）鼓励学生利用估算来验证计算结果，养成好习惯。

现在学生们有时用计算器计算，有时用精确的笔算，那么结果对不对呢，特别是积的位数、商的位数是否准确？可以先用估算的方法来确定一下它大致的取值范围，帮助学生验证计算的结果。有这样一个例子，231加上416，有位学生计算得500多，同桌看见后，说你这肯定不对，200多加400多，肯定得600多，怎么也不能是500多。可见，让学生感觉到估算的必要性并养成好的估算习惯，是很重要的。学生通过不断地体会估算给他带来的帮助，就能逐渐提升其估算意识。

（4）引导学生在问题情境的对比中选择估算或精确计算。

作为数学教师，要想办法搜集或者捕捉一些好的素材，在具体的问题情境当中让学生去感受，什么样的问题解决需要近似值，哪些问题解决一定要算出精确值，比如像刚才一家三口出去吃饭的例子，只要估算即可。但作为饭店的收银员就需要精确计算，估算显然不行。

估算教学是一个新内容，我们没有更多的经验积累。虽然生活中的例子不少，甚至估算比精算用得还多，可是真正好的例子，能够搬到课堂上来用的，就很少了。特别是适合儿童的、贴近儿童现实生活的例子就显得有些匮乏。这给老师们提出了一个新的挑战，需要不断地去积累。

2.形成估算策略。

首先来看下面的课例，再结合课例来谈学生估算策略的培养。

【案例2】估算

片段一：创设情境，使学生感受估算的价值。

（1）师：老师在海报上看中了几样商品，准备去超市购买，请同学们帮我想一想：带100元钱够不够？（保温杯：9.80元，巧克力：23.60元，牛奶：16.60元，清洁剂：9.70元，面粉：14.00元，饼干：25.20元。）

（2）学生用凑整的方法进行估算。教师引导学生分别站在顾客和收银员的角度来选择不同的计算方法（估算还是精确计算）。而后，请学生回想生活中用到过估算的例子。

片段二：展示不同的估算方法。

（1）师：大家对估算都有一定的经验，下面我们就来试一试：

某校五年级6个班的人数统计如下：

你能估算出五年级大约有多少名学生吗？

（2）反馈。

生1：把这6个数都看成30，30×6=180（人），我估算的结果大约是180人。

生2：把这6个数都看成40，40×6=240（人）。

生3：我把37、35、38和36看成40，把33和32看成30，40×4+30×2=220（人）。

生4：这6个数都在35上下，如果把这6个数平均一下大约就是35，所以可以把35看作中间数，35×6=210（人）。

（3）教师评价：同学们的估算方法都有一定的道理。老师在同学们估算的同时悄悄算出了精确结果，你们想不想看一看？

（4）公布年级实际的总人数：211人。师：看到这个结果你们有什么新的想法？

（5）学生开始将精确结果和自己的估算结果进行比较，并对自己的估算方法进行反思。

生1：我都看成30，所以就估少了，用中间数的方法最接近。

生2：我都看成40，就估高了，要比240少。

生3：都看成30，每个数都少了，所以估算结果就比实际结果少；都看成40，每个数都多了，所以估算结果就比实际结果多。用“四舍五入”和取中间数的方法要好一些。

（6）教师小结：同学们都发现了用“四舍五入”和取中间数的方法得到的估算结果和准确结果比较接近。但都看成30或都看成40的方法也有它的价值。我们可以看到实际的结果一定比180大，同时它要比240少，也就是在180和240之间，这两种方法就为我们划定了准确值的范围。

这个课例中，教师给学生出示的问题情境很巧妙，使学生产生了估算需要。更为可贵的是，教师能在课堂教学过程中追问学生：生活当中哪儿还用到估算？这就是对学生估算意识的培养，久而久之学生的估算意识就会慢慢形成。

这节课的后半段，学生用了那么多种不同的策略来进行估算，可谓精彩纷呈。特别是，教师又抛出了一个精确值，让学生用自己估算的结果和这个精确值去比较，学生有了第二次交流和反思，在这个过程中，学生所获得的不仅仅是一种估算的策略，同时也积累了一些估算的方法或者能力，如尽量地逼近精确值、合理地调整、把握取值范围等。

本节课，教师是将估算意识的培养作为一个重要的目标来开展教学的，所以在好几个环节都在用心地去发展学生这种估算的意识，包括问题的引入、结合生活实际举例等，另外教师还很注重估算策略的调整。下面就估算策略教学提出一些建议。

（1）鼓励学生解释估算的思路和理由。

教师应鼓励每个学生尽可能清晰地表述自己的思路和理由，适当地鼓励学生总结估算的策略，因为这确实是一个经验积累的过程。经验积累是重要的，但需要学生自己不断反思和调整原有的认识。凡是合理的估算策略，我们都应当给予肯定。

（2）让学生在对估算和精确计算结果的比较中不断提高估算能力。

以上面“估算”这节课为例，一般教师看到学生用多样的方法、策略来进行估算，可能就很高兴了，往往就在这儿要收尾了。而此时授课教师却提出了一个很有价值的问题：“老师在同学们估算的同时悄悄算出了精确结果，你们想不想看一看？”又一次引起了学生热烈的讨论，当把自己的估算结果和精确值进行比较，同时也和其他同学的估算结果进行比较的时候，学生就发现了有的取值范围可能更加合理，有的估计得远了些。怎样使估算结果更接近准确值呢，学生开始了反思，自觉地进行二次估算方法的选择，这种经验的积累，对不断提高判断能力、选择能力乃至估算能力会有重要的帮助。

（3）让学生掌握具体的估算策略。

这些策略主要有：①凑整的方法。②取一个中间数。比如32，37，30，39这四个数求和，这些数都很接近35，有的比35多一点，有的比35少一点，就取一个中间数35，直接用35×4就大约地计算出了这几个数相加的结果。③用特殊的数据特点进行估数。如126×8，就可以想到125×8，得1000。④寻找区间。也就是说寻找它的范围，也叫做“去尾进一”，“去尾”就是只看首位，估得的结果就是它至少是多少，“进一”就是首位加一，假如说278，我们就将其看成300，首位加一，也就是它最多可能是多少，这样得到一个范围，就是它的区间范围。⑤两个数，一个数往大里估，一个数往小里估，或者一个数估，一个数不估。⑥先估后调。

四、如何评价估算？

关于估算的评价，我们先来看一个案例。

【案例3】TIMSS测试

TIMSS（为“国际数学和科学评测趋势”的缩写）测试是由国际教育成就评价协会发起和组织的国际教育評价研究和评测活动，也是有史以来最大、最全面、最严格的国际比较研究项目。曾于1995年、1999年、2003年做过3次测试。这3次测试是当代青少年数学教育和科学教育的重要的国际比较研究，对我国的数学教育和科学教育有一定的启发和借鉴意义。

在TIMSS测试中，也有考查学生估算能力的题目，下面是其中的一些：

1.史密斯家每星期的用水量是6000升，他家每年的用水量大约是多少升？

A.30000B.240000

C.300000D.2400000

E.3000000

2.约翰想在磁带上录5首歌，每首歌所用的时间如下表所示：

估计一下他录完这5首歌需要多少时间，并解释你的结果。

（正确答案：①将每段时间正确地按分钟取整。如：3+3+3+3+4或3+3+3+3+3；②将每段时间正确地近似到5秒，10秒，15秒或30秒，然后相加；③没有显示计算过程，但有类似于“四舍五入”或“化为整分钟”的表述；④将各段时间都按3分钟相加，然后用15分钟加上14秒；⑤其他合理的答案。错误答案：①每段时间都进行四舍五入，但其中出现了一些错误；②将13分134秒改写成14分34秒；③其他错误答案。）

3.保罗用$5去购买牛奶、面包和鸡蛋。当他到达商店时，发现这三种食品的价格如下图所示：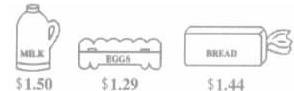

在下列哪种情况下使用估算比精算有意义？

A.当保罗试图确认$5是否够用时；

B.当售货员将每种食品的价钱输入收银机时；

C.当保罗被告知应付多少钱时；

D.当售货员数保罗所付的费用时。

这些题目究竟能给我们什么重要的启示呢？

在估算或估测过程中，由于每个学生都有自己的想法，面对同一问题所采取的策略不尽相同，因而估算结果往往不是唯一的，是不是估算的值离精确值越接近越好呢？如何评价估算？上述第2题的评价标准是很宽松的，只要学生的想法合理就可以了，这与我们平时对于估算的评价有些不同，我们对于估算结果的接受范围过窄。

保罗购物的题目更是让人耳目一新。我们平常见到的估算题目模式比较单一，大多都是估一估价钱够不够，而这道题的问法却是“在下列哪种情况下使用估算比精算有意义”。这样的提法使我们很受启发。这样的问题可以测量出学生的估算意识和估算能力。

那么我们在实际教学中该如何对估算进行评价呢？

首先把估算分为两种：一种是根据实际问题进行的估算；一种是脱离实际问题的情境、纯算式的估算。

1.根据实际问题选择合理的估算策略，结果合理方为正确。也就是说，学生只要能够解决实际问题，那这个估算结果就应该是合理的。

2.纯算式的估算，结果落在区间内方为正确；但要根据不同年龄学生的认知水平，给予有针对性的评价。有一些题目，脱离了实际问题情境，属于纯算式的估算，在这种情况下，我们提出：不能简单地把估算结果是否与精确值最接近作为唯一的标准，只要落在区间内，就视为是合理的。这个区间也就是它的取值范围。

同时，对不同年龄的学生要有不同的评价标准。如低年级学生刚刚接触估算，它的估算结果落在区间内，但是范围比较大，我们觉得也是可以的。高年级的学生已经有了一定的估算经验，就要引导他们不断地进行反思、调整，使估算的结果能落在更合理的位置上。举个例子来说：78×365的结果大约是多少，刚开始学习的时候，学生可能这样估：70×300，80×300或者80×400，我们都可以视其为合理的。等有了一定的计算技能以后，老师要引导学生不断地进行反思，例如，可以估成80×350，这时候的范围就比原来要小多了。

另外，从命题的角度来看，能不能让题目更适合学生用估算的方法来解答？这样有利于学生估算意识的培养，提升估算策略的选择能力。

3.只要估算结果落在合适的数量级中，视为合理。如上述TIMSS测试的第1题，就是在考查学生的数量级概念掌握情况。只要学生的估算结果落在合适的数量级中就可以视为合理。

总之，关于评价的问题还有待于进一步研究。但我们认为，学生们估算的策略不同，只要是合理的，就应当鼓励他们大胆地尝试，积极解释自己的观点。在这个过程当中，肯定会有很多有价值的东西涌现出来，教师要小心翼翼地去呵护这种探究精神，不要轻易地用一两句话否定一种方法，而应给他们一种宽松的氛围，让他们不断地学会调整，学会反思，提升判断能力。教师要不断地站在学生的角度去思考、挖掘这些方法的思维价值，利用这种近似的意识来发展学生的数学思维。

（参与本文撰写的有：吴正宪、张秋爽；参与本文讨论的有：张丹、周玉仁、许淑一、姚建、张岭、王彦伟。本文由教育部基础教育课程教材发展中心新课程远程研修小学数学课程团队提供的讲稿改编而成。）