挖泥船破损强度分析研究
上海交通大学 船舶海洋与建筑工程学院 上海 200030
我国近几年来港口与航道等基建工程的发展使得挖泥船的需求量与日俱增。
挖泥船工作环境特殊,容易在施工和航行区域受损,船体受损后的安全性与生存能力、破损后能承受的终极载荷以及破舱后的剩余强度等问题受到重视。现有规范中仅对完整状态时的总纵强度和破损稳性有相关的规定,但对破损后船体的剩余强度未作明确的要求。因此,有必要对挖泥船进行破损后船体的剩余强度研究。
1 破舱后的载荷计算
1.1 静水载荷
应用经典船体梁理论分析船舶破损后的弯矩剪力。首先要确定船舶破损后的平衡浮态,采用浮力损失法确定破舱后船舶的平衡浮态。经计算符拉索夫计算曲线可得破损后的全船浮力曲线b(x)及相关要素。
b(x)=V(x)-b′(x)
式中:V(x)——平衡浮态下全船浮力曲线;
b′(x)——破舱段的损失浮力曲线。
已知重量曲线w(x),则可得全船载荷曲线q(x)
q(x)=w(x)-b(x)
破损后船舶静水剪力和静水弯矩分别为:

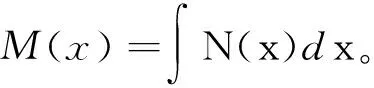
某单长泥舱的挖泥船主要的船体要素为:
Lpp=108 m,B=21 m,
D=9.2 m,d=7.15 m。
计算挖泥船两种工况(最小干舷时和空载)的破损,泥舱舱底(船中的#80)破损。最小干舷破损时渗透率取0.60,空载破损时渗透率取0.95。船体破损前后的静水弯矩剪力分布及极值比较分别见表1和图1~4。

表1 破损前后静水弯矩剪力极值

图1 最小干舷破损前后静水剪力比较

图2 最小干舷破损前后静水弯矩比较
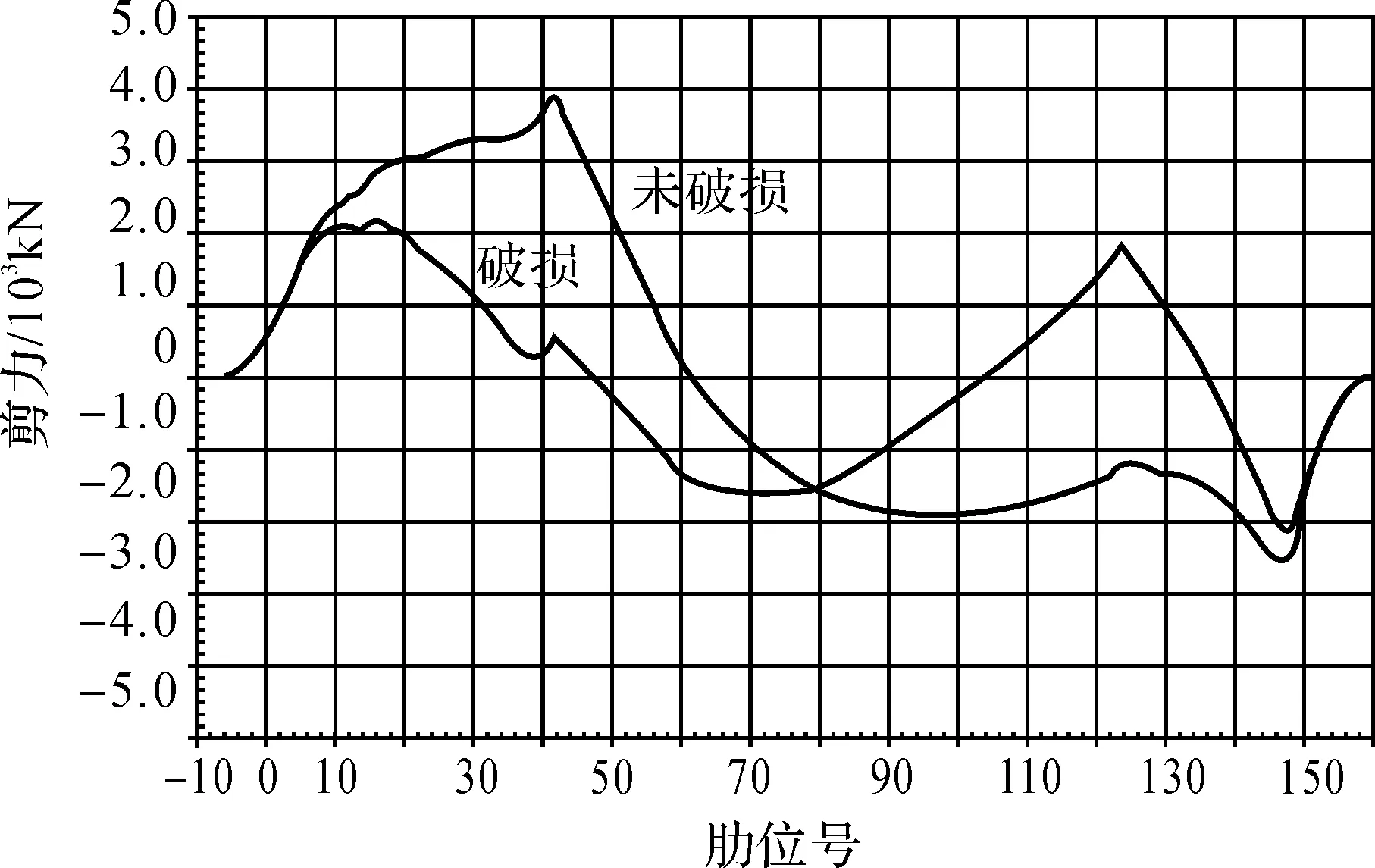
图3 空载破损前后静水剪力比较

图4 空载破损前后静水弯矩比较
1.2 波浪载荷
国际船级社协会(IACS)己统一了波浪载荷计算式,波浪弯矩设计极值计算如下。
1) 中垂波浪弯矩Mw(-)为:
Mw(-)=-0.11CwL2B(Cb+0.7)
2) 中拱波浪弯矩Mw(+)为:
Mw(+)=0.19CwL2BCb
2 极限强度非线性有限元分析
基于文献[3]建立的计算完整和破损船体极限强度的非线性有限元理论对挖泥船的泥舱段进行有限元分析。文献[3]对非线性有限元法分析结果与实验数值进行了比较验证,计算得到的极限强度与试验结果比较吻合。
2.1 计算模型
取肋距为网格基本单位;舱段长49.0 m,型宽21.0 m,型深9.2 m,甲板为大开口结构;主要纵向构件的结构尺寸见表2。
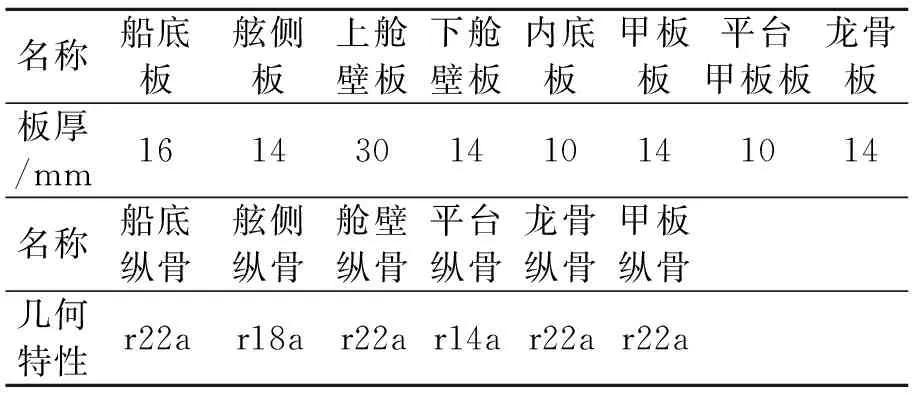
表2 主要纵向构件的尺寸特性
整个结构共有34 796个单元,21 006个节点;有限元模型见图5。

图5 舱段有限元网格划
2.2 材料、边界条件及载荷
用刚性面来处理两个舱壁,把舱段边界条件理想化为类似两端固定梁边界,如表3所示。材料采用船用钢Q235,屈服强度σs=235 MPa,杨氏模量201 GPa,泊松比0.3,强度极限σb=375 MPa,伸长率δ=0.26。两端舱壁均为加载端,参考弯矩由规范设计引出Mr=σs·W0
式中:W0——规范要求的最小剖面模数。

表3 舱壁边界条件
2.3 屈服准则
选用von Mises屈服应力准则,材料在复杂应力状态下的变形能达到了单向拉伸屈服时的变形能,材料开始屈服,即等效应力屈服准则:

2.4 计算结果
基于非线性有限元软件对以上舱段进行计算,旨在求得其在参考载荷RL作用下,结构达到极限状态能承受的最大比例的载荷因子LPF,即:
极限承载能力=RL×LPF
文中初步计算了完整舱段的中垂及中拱状态下的极限承载能力。中拱时载荷因子为2.34,中垂时载荷因子接近1.00,结构线性失效,这是由于甲板屈曲破坏引起的。两种工况下舱段结构能承受的极限弯矩如下。
1) 中拱极限弯矩Mult为:
Mult(+)=Mr×LPF= 1.59×106kN·m
2) 中垂极限弯矩Mult为:
Mult(-)=Mr×LPF= 6.77×105kN·m
从图6、7中可以看出:中拱时结构为甲板受拉屈服失效,船底受压屈曲失效,而极限中和轴附近保持弹性;中垂时为甲板结构压缩失效,船底结构应力相对较小,这是由甲板大开口结构造成的。中拱时载荷因子LPF和船舯底部节点位移的关系以及中垂时载荷因子LPF和船舯甲板节点位移关系见图8,9。

图6 中拱等效应力分布及结构变形图

图7 中垂等效应力分布及结构变形图

图8 中拱载荷因子和船舯底部节点位移的关系

图9 中垂载荷因子和船舯甲板节点位移的关
一系列甲板板厚计算表明,当甲板板厚达到40 mm时,线性屈曲情况得以改善。等效应力分布见图10,载荷因子LPF和船舯甲板节点位移关系见图11。

图10 中垂等效应力分布及结构变形图

图11 中垂载荷因子和船舯甲板节点位移的关系
3 计算结果分析
破损前后的弯矩剪力与规范及极限承载弯矩数据结果见表4。
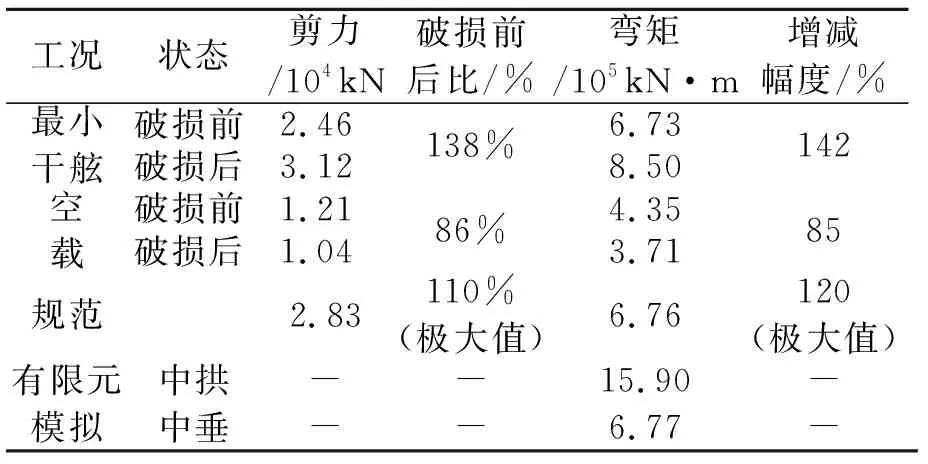
表4 理论和有限元模拟结果比较
3.1 破损前后弯矩剪力
计算破损前后弯矩剪力变化,目的在于求得破损前后弯矩剪力曲线极值变化。船舶破损后最小干舷工况剪力弯矩极值明显增加,最大弯矩是未破损前的142%,最大剪力是未破损前的138%,这将对此类船舶的生存能力形成严峻的考验;空载工况则恰恰相反,破损后减小了原来船体中拱的程度,破损后剪力弯矩极值减小。
3.2 规范校核及安全余度
用利用系数UF来表达规范设计载荷相对于船舶破损后载荷的余度。
1) 弯矩利用系数UFM为:
UFM=(Ms+Mw)/Mr;
2) 剪力利用系数UFN为:
UFN=(Ns+Nw)/Nr。
最小干舷利用系数UFM=1.2,UFN=1.1,超过了规范设计载荷;
空载工况利用系数UFM=0.55,UFN=0.37。
相对于极限承载能力来讲,计算时参考载荷RL取规范设计弯矩,所以有限元计算结果中的最终载荷因子LPF就是规范设计的安全因子,中拱为2.34,中垂为1.01。
3.3 破损弯矩与极限载荷比较
用剩余强度因子RRF来评估完整状态的极限载荷相对于破损后载荷的余度。
RRF=破损后载荷极值/完整时极限承载能力
最小干舷
RRF=[Ms(- )+Mw(- )]/Mult(- )
=(8.50×105)/(6.76×105)=1.25>1;
空载工况
RRF=[Ms(+)+Mw(+)]/Mult(+)
=(3.71×105)/(1.59×106)
=0.23<1;
最小干舷工况破损后的弯矩超出了中垂状态时的极限承载弯矩,舱口围板和甲板结构受压屈曲破坏。船体甲板部分结构过于薄弱,应加强船体剖面中和轴以上的结构如甲板板的板厚及加强筋的尺寸。
4 结论
1) 通过规范计算校核,最小干舷工况破损进水后不满足结构要求,若在设计阶段就考虑需满足破损后的总纵强度,则例船中横剖面结构需重新设计,应该加强甲板部分的结构强度,以满足实际要求。
2) 规范若是考虑此类挖泥船的破损后的强度,必须加强针对甲板结构的相关规定。
3) 相对于实际结构的极限承载能力,最小干舷工况破损后的载荷将使甲板的加筋板格受压而屈曲,致使甲板屈曲失效,剖面模数急剧下降,严重的最终导致船舶断裂。
4) 有限元模拟的中垂极限弯矩和规范的设计值比较接近,有效地论证了结论1)。
[1] Hai-Hong Sun, C. Guedes Soares .An experimental study of ultimate torsional strength of a ship-type hull girder with a large deck opening[J]. Marine Structures,2003,16:51-67.
[2] 徐向东,崔维成,冷建兴,孙兆康,祁恩荣.箱型梁极限承载能力试验与理论研究[J].船舶力学.2000(5):36-43.
[3] 祁恩荣,崔维成.破损船体极限强度非线性有限元分析[J].船舶力学,2005(5):83-91.
[4] 张国栋,李朝晖.船体破损后外载荷和船体极限弯矩[J].中国造船,1997(4):28-33.
[5] 陈宾康.船舶静力学现代计算法[M].大连:大连海事大学出版社,1995:200-204.

