波浪运动补偿稳定平台系统液压机构的仿真试验

，，

(华南理工大学 交通学院，广州 510641)

海上工作船受风、浪、流、潮等影响，不可避免地产生摇摆和升沉，直接影响海上作业的进行。为了保证工程的进行，可在船舶上建立一个具有波浪运动补偿功能的稳定平台系统。该系统是机电液一体化的大型装置，技术难度高，结构复杂，又在远离海岸的深海运作，对可靠性要求极高。由于稳定平台系统造价昂贵，不可能建造实物模型来进行试验。而计算机仿真和模拟试验是及早处理和改进设计，加速催化技术成熟及保证系统性能稳定可靠的有效手段。因此，利用Simulink仿真软件对系统进行数学建模和仿真，并对不同控制算法的仿真结果进行分析和比较。

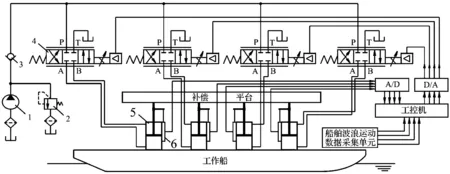
1-液压泵；2-溢流阀;3-单向阀;4-电液比例方向阀;5-液压缸;6-位移传感器图1 波浪运动补偿稳定平台系统的液压原理图

1 系统的工作原理

补偿稳定平台系统组成见图1。

由船舶运动数据采集单元采集到各个液压缸位置处的船舶摇摆升沉信号，然后传输到工控机进行运算，并通过数模转换和相关的电控制单元按一定的控制策略输出控制信号给电液比例方向阀，从而控制液压缸往船舶运动的相反方向运动，来抵消船舶摇摆深沉对补偿平台的影响，使补偿平台不随船舶运动而运动，始终保持水平，最终实现运动补偿[1]。

2 阀控缸系统数学建模

2.1 电液比例方向阀的数学建模

2.1.1 比例方向阀电磁铁线圈回路

系统所用的电液比例方向阀集成有位置传感器和放大器，通过位置传感器的反馈信号，能对阀芯位置进行高精度的闭环控制。由其线圈回路的电压方程和比例放大器的电压放大方程[2]进行拉氏变换，并联立求解，可得

(1)

式中:I——电磁铁线圈电流；

Ug——比例放大器的给定电压；

Xv——阀芯位移；

Ke——放大器的电压放大系数；

Ki——线圈回路增益；

ωi——线圈回路转折频率；

Kif——电流负反馈系数；

Kxef——阀芯位移负反馈系数。

2.1.2 阀芯位移输出模块

求解比例方向阀阀芯力平衡方程可得到阀芯位移输出模块的传递函数为[3]：

(2)

式中：Ksv——比例方向阀的电流位移增益；

ωsv——阀芯的固有频率；

δsv——比例方向阀的阻尼比。

2.2 液压缸的数学建模

对阀控缸的3个基本方程[4]进行拉氏变换，并联立求解，可得：

(3)

式中：Xp——液压缸活塞位移；

FL——作用在活塞上的外负载力；

Ap——液压缸活塞的有效面积；

Kq——流量增益；

Kce——液压缸的流量压力系数；

ω1——液压缸容积滞后频率；

ωh——液压缸-负载质量系统固有频率；

δh——液压缸-负载质量系统阻尼比。

3 控制器的设计

系统控制器采用了Fuzzy-PI复合控制器(见图2)，既发挥了模糊控制器鲁棒性强，抗干扰能力好，动态性能优良的特性，又发挥了PID控制器稳态精度高的特点。

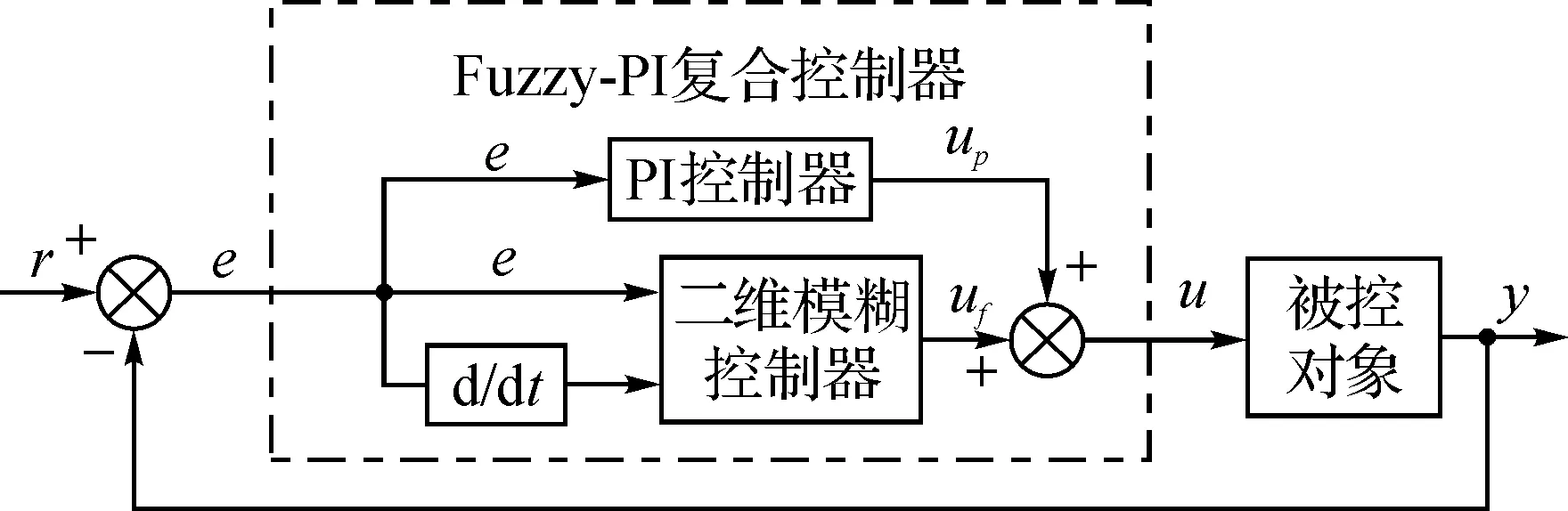
图2 Fuzzy-PI复合控制

3.1 模糊控制器的设计

模糊控制器输入为系统误差e和误差变化ec，输出为控制量uf，它们量化为13个等级。

量化论域：{-1.00, -0.75, -0.50, -0.35, -0.20, 0.10, 0, 0.10, 0.20, 0.35, 0.50, 0.75, 1.00}

模糊子集：{NB,NM,NS,ZO,PS,PM,PB}

隶属函数取三角型隶属函数，见图3；模糊控制规则见表1。

图3 隶属度函

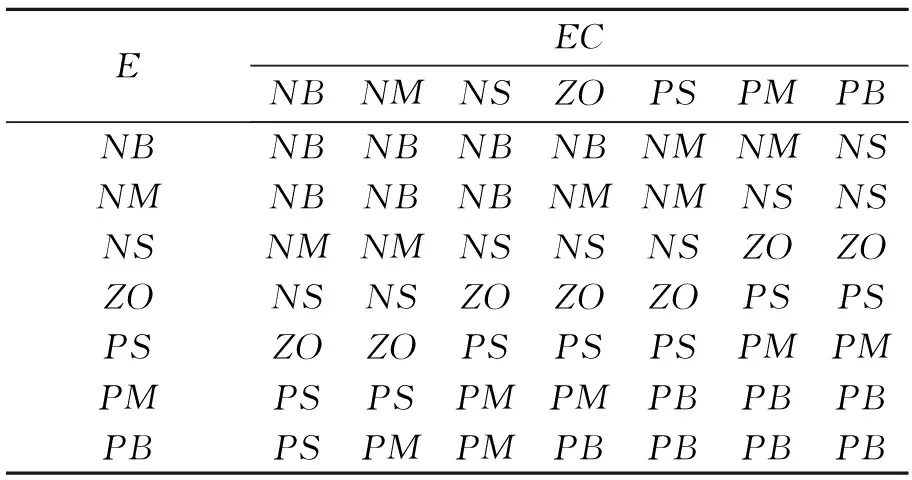
表1 模糊控制规则

3.2 PI控制器的设计

为了消除静态误差，同时避免大偏差时的积分积累，PI控制器设计采取了积分分离算法[5]，人为设定一阀值ε，当|e(k)|>ε时，也即偏差值|e(k)|比较大时，只采用P控制，可避免过大的超调，又使系统有较快的响应；当|e(k)| ≤ε时，也即偏差值|e(k)|比较小时，采用PI控制，从而保证了系统的静态控制精度。

(4)

k——采样序号；

e(k)——系统输入偏差量；

up(k)——PI控制器输出控制量；

Kp——比例系数；

Ki——积分系数。

4 基于Simulink的系统仿真模型

Simulink是Matlab提供的一个可用来对动态系统进行建模、仿真和分析的工具软件包。图4为利用Simulink提供的各种仿真模块，并根据式(1)、(2)、(3)及系统的信号传输关系建立起来的系统仿真模型。其中，液压缸的负载fL暂取固定载荷。Fuzzy-PI控制器模块子系统内部结构见图5。

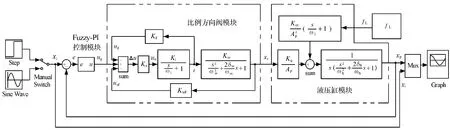
图4 系统的Simulink仿真模型

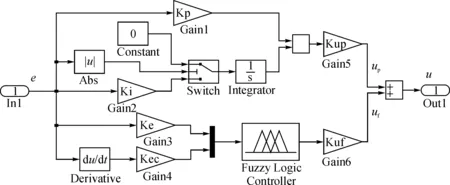
图5 Fuzzy-PI控制器模块子系

5 仿真试验

为了对波浪运动补偿稳定平台系统的性能进行研究，根据相似原理，建立一个缩小比例的简化试验模型，并对该模型进行了数学建模和仿真。建立的模型系统采用HTS-SB60A3型液压泵站、意大利ATOS公司的DLHZO-TE-040-L71型高性能电液比例方向阀、LEIERDA公司的MOB 32×250-FA-LB型液压缸。缸行程为250 mm，缸内径32 mm，缸活塞杆外径16 mm，液压缸的负载约为400 N。系统分别采用了PID控制、模糊控制和Fuzzy-PI复合控制3种控制算法进行试验比较。

图6为其阶跃响应仿真图。由图6可以看出，采用普通的模糊控制算法，系统存在着较大的稳态误差，而Fuzzy-PI复合控制加入了积分环节后，系统的稳态误差明显减少；同时，Fuzzy-PI复合控制的超调量较PID控制明显减少。

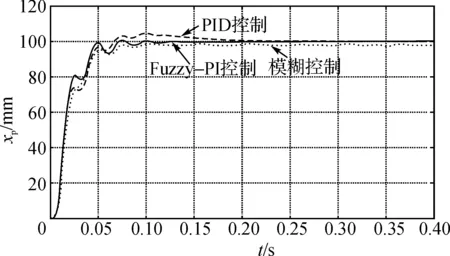
图6 系统阶跃响应曲线图

图7为采用Fuzzy-PI复合控制时，液压缸跟随正弦位移输入信号的仿真曲线。图中，xi为输入的正弦位移参考信号，xp为液压缸的跟随曲线。从图中可以看出，系统对输入信号的跟随性能良好，但存在1 h的滞后。当系统负载加大时，滞后也相应变大。经实测模型试验对比，仿真结果与模型试验结果比较吻合。

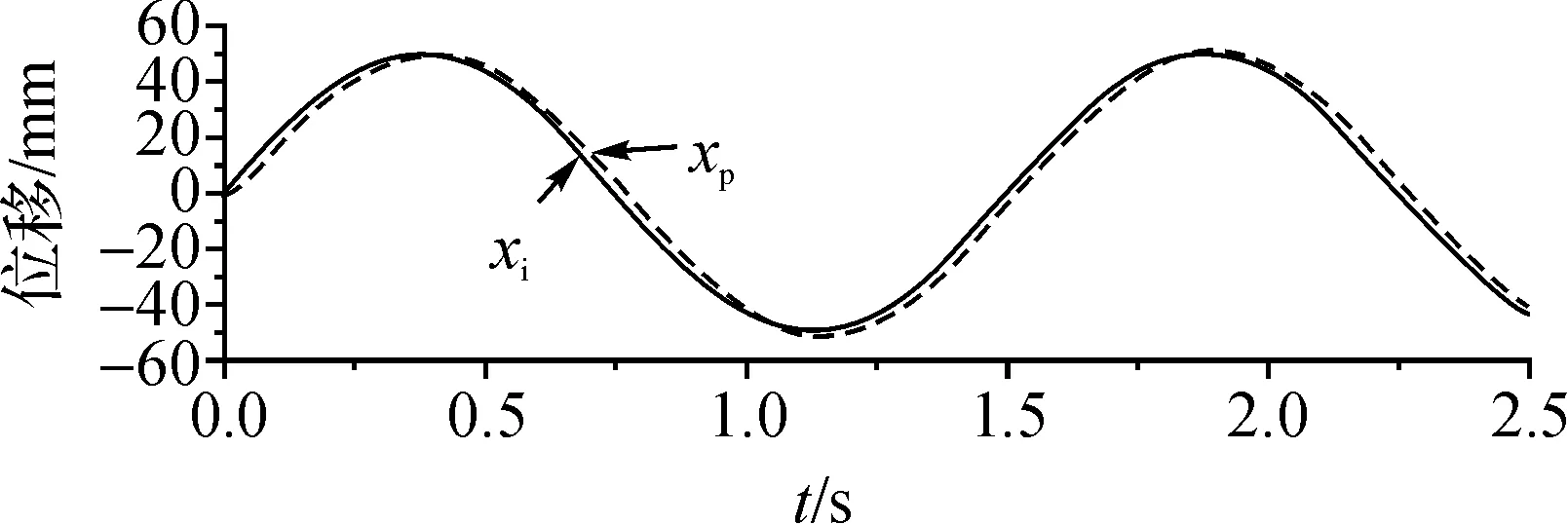
图7 液压缸位移跟随曲线

6 结论

利用Simulink进行计算机仿真，具有简单、直观的特点，能方便地建立系统的动力学模型，同时还充分利用了Matlab强大的计算功能和编程技术，提高了仿真计算的灵活性和效率。通过Simulink仿真，可得到系统的动态响应以及各个状态变量之间的相互关系，有助于确定系统的有效控制算法，优化系统参数，从而为系统的设计与制造提供了一些宝贵的先验知识。

仿真结果表明，Fuzzy-PI复合控制的超调量明显减少，大大消除了稳态误差，系统响应快。其结合了模糊控制动态特性好和PID控制稳态性能好的特点，控制效果均优于常规的PID控制和模糊控制。

从位移跟随曲线可以看出，系统存在着一定的滞后，在负载加大时，滞后变得明显。这不单与系统机构的响应速度有关，还与所采取的反馈控制算法有关。因为反馈控制属于被动式控制，是在误差发生后，才开始控制机构往误差减少的方向运动，所以必然存在着一定的滞后。要有效地消除滞后，就必须在误差发生前就对系统进行控制，因此有必要考虑前馈控制和反馈控制相结合的控制模式，加入有效的预测算法等。这些都是今后的研究重点。

[1] Ye Jiawei, Chen Yuanming, Wang Dong-jiao, et al.Wave motion compensation scheme and its model tests for the salvage of an ancient sunken boat[J].China Ocean Engineering, 2006, 20(4): 635-643.

[2] 许益民.电液比例控制系统分析与设计[M].北京:机械工业出版社,2005.

[3] 卢长耿,李金良.液压控制系统的分析与设计[M].北京:煤炭工业出版社,1991.

[4] 李连升,刘绍球.液压伺服理论与实践[M].北京:国防工业出版社,1990.

[5] 陶永华.新型PID控制及其应用[M].北京:机械工业出版社,2002.