撞头形状对双壳结构耐撞性能影响分析
,,,
(华中科技大学 交通科学与工程学院,武汉 430074)
船舶碰撞往往会造成船体破损,对于油船和化学品船,碰撞事故会造成原油或化学品的泄漏,导致严重的环境污染。在船舶碰撞过程中,船首作为主要作用方,其形状直接对碰撞产生影响。
王自力[1]等人通过研究撞击参数如速度、撞击角度和撞击位置对双层舷侧结构碰撞响应的影响,结果表明随着撞击角度增加,结构的破裂失效会提前,但是撞击速度的少量变化并不会显著影响船体的碰撞损伤特性。Krzysztof[2]通过有限元仿真技术模拟双层壳结构在锥体撞击下的响应,通过调整相关参数研究其对双层壳结构抗撞性能的影响。本文采用非线性有限元仿真技术,研究四棱台形和圆锥球头形撞头对双层壳抗碰撞性能的影响。
1 撞头及双层壳结构的有限元模型
1.1 仿真中使用的材料模型
船舶在撞击过程中首部的刚度一般远远高于被撞船的舷侧结构,在船舶碰撞研究时通常将首部结构看作刚性体,不考虑首部的变形和吸能。因此,将撞头近似看作刚性体,撞头的形状分别为四棱台和圆锥球头。单元类型的选择上,对于被撞头撞击的附近区域,变形相对比较大,这里选用huges-liu壳单元,且沿厚度设置5个积分点,这种单元的特点是消耗更多时间但在处理大变形以及翘曲问题效果更好。其他区域相对来说变形比较小,均采用默认的Belytsch-Tsay单元,这种单元求解效率最高,很经济,也是LS_DYNA默认的单元类型。
双层壳考虑采用线性随动硬化材料,密度为7.8×103kg/m3,弹性模量210 GPa,泊松比0.3,剪切模量1.18 GPa,屈服应力0.235 GPa;刚性撞头。为了使撞击拥有足够的动量,同时为了使得两种撞头的初始动量一致,四棱台形撞头的密度取值为7.8×107kg/m3,圆锥球形撞头的密度取值为4.292×107kg/m3。弹性模量210 GPa,泊松比0.3。
1.2 材料的破裂失效准则的选择
在材料失效准则的选择上,采用定义失效应变来判断模型失效。失效应变的合理选择非常重要,一般认为失效应变的选择跟单元尺寸的大小有关;单元的尺寸越大,失效应变就应该取得越小[3]。在船船碰撞中,10%的应变适合大多数情况,因此取失效应变为0.1[4]。
1.3 材料应变率的考虑
碰撞过程是一个动态响应过程,材料的动力特性影响不能忽略。大部分用的钢材为低碳钢,对应变率高度敏感,屈服应力和拉伸强度极限随应变率的增加而增加,所以考虑应变率的影响。材料应变率敏感性的本构方程比较多,采用与实验数据吻合的较好的cowper-symonds本构方程:
(1)
式中:σd——动屈服应力;
σs——静屈服应力;
ε——塑性应变率;
D、q——材料常数,取D=40.4,q=4[5]。
1.4 接触的定义
碰撞过程中,一方面撞头与双层壳结构之间会发生接触;另一方面,由于双层壳结构大变形和挤压的影响,双层壳构件之间也会产生接触。在接触类型的选择上,采用自动单面接触,单面接触可以用在一个物体表面的自身接触或两个物体表面间的接触。单面接触中,程序将自动判定模型中哪些表面发生接触,不用人为定义主、从接触面。与隐式模型过多定义接触面将大大增加CPU时间不同,在显示模型中定义单面接触只会较少地增加CPU的时间。对于模型中壳单元法向方向可能出现不一致的情况最好采用自动接触算法[6]。考虑到单面自动接触不能自动输出接触力,所以通过建立传感器接触类型来输出接触力。因为接触间的摩擦作用不会影响到结果的趋势,所以不考虑摩擦。
1.5 网格的划分和模型的尺寸布置
在网格划分上,考虑到冲击的变形较大,网格划分要尽量精细,特别是在中间被撞区域,同时也要考虑计算的效率,本文双层壳的最小单元尺寸为100 mm。单元模型中有5万多单元,撞头从双层壳的法向以一定的速度撞击双层壳。
双层壳长28 m,宽10 m,内外壳的间距为2 m,在双层壳间布置的纵向腹板间的间距为2 m,结构几何示意图见图1。

图1 双层壳结
1.6 载荷和约束
双层壳的周边节点均采用全约束,撞头除了撞击方向的平动自由度松弛外,其余自由度全部约束。为了减少由于过细的单元划分带来的计算时间剧增的影响,同时,为了给撞头足够的动量,撞头的初始速度取为v=8 m/s。
1.7 撞头的几何特性
为了尽量消除尺寸上的差距而突出撞头形状对撞击的影响,两种撞头的尺寸设置如下:
四棱台形撞头的尺寸,上底面边长均为3.6 m,上底面长对角线为6.0 m,短对角线为4.0 m,下底面边长为上底面边长的1/10,棱台高1.8 m。圆锥球形撞头的尺寸,底面直径为6 m,高为1.8 m,撞头几何形状侧视见图2、3。

图2 四棱台形撞头
图3 圆锥球形撞头
2 仿真计算的结果与分析
2.1 撞头形状对碰撞区结构损伤变形的影响
图4、5分别表示双层壳结构受撞区域在四棱台形撞头和圆锥球形撞头撞击下损伤变形的时序结果。

图4 四棱台形撞头下双层壳结构损伤的时序结
结构的损伤变形主要集中在撞击区域,这也说明船体结构抗撞能力的提高应着眼于容易遭受撞击的薄弱区域,没有必要大范围地对结构进行增强改造。
撞头的形状不同,损伤的形式也必然不一样,并且可以由时序图比较发现,四棱台撞头在t=0.030 s时就已经把外壳击穿,而圆锥球形撞头在t=0.084 s时才击穿外壳,这是由于相对四棱台形撞头来说,圆锥球形撞头的几何变化平滑,相对更不容易击穿外壳。由于撞头的初始动量相对来说比较大,从图中可以看出双层壳的损伤变形也相对比较严重。

图5 圆锥球形撞头下双层壳结构损伤的时序结
2.2 撞头形状对碰撞力的影响
图6为圆锥球形和四棱台形撞头碰撞过程中碰撞力随撞深的变化曲线,因为撞头开始与双层壳碰撞之前存在一小段间距,所以曲线没有经过原点。

图6 碰撞力-撞深曲
从图6可以看出,在整个碰撞过程中,结构出现多次卸载现象,碰撞力与撞深之间存在着很强的非线性关系。碰撞开始后,由于外壳的抵抗作用,碰撞力迅速增加;但随着外壳的变形和失效,碰撞力出现局部下降的趋势;随着碰撞过程的继续,撞头与腹板相继开始接触,由于腹板的抵抗作用,碰撞力再次开始攀升;随着腹板的变形和失效,曲线又表现为局部下降;当碰撞过程进行到撞头与内壳接触时,碰撞力又迅速拉升。同样地,当内壳的变形的增大导致逐渐失效,碰撞力又迅速下降。由于模拟的过程比较长,撞头基本上都穿过了双层壳,因此表现在图上就是碰撞力最后几乎降到零,图中三个明显的峰值点分别对应外壳,腹板,内壳出现大面积失效时。
比较两条曲线,碰撞力随撞深的变化趋势基本类似;差别在于:四棱台形撞头的碰撞力曲线的局部卸载现象较球形撞头明显而且频繁。这是由于四棱台形撞头具有“锋利”的棱边,被碰撞的材料更容易被割裂而失效。随着失效单元的被删掉,在等量撞深下,与双层壳接触的有效单元,圆锥球头形要多于四棱台形撞头。这就导致了图中所示球头碰撞力曲线明显高于棱台形撞头。另外,从碰撞力曲线的起步阶段可以看出,第一次卸载的出现棱台形要提前与球形,这也正说明棱台形撞头更快的击穿了外壳,这与图4、5反映的情况一致。
2.3 撞头形状对内能和动能影响分析
图7和图8分别表示两种情形下变形能和刚体动能的变化趋势。碰撞初始,只有刚体的动能存在,由于没有考虑撞头的变形以及摩擦的影响,碰撞过程中,随着双层壳结构的变形特别是塑性变形的发生,刚体动能逐渐转化为双层壳的变形能。
图7中曲线逐渐上升的趋势和图8中曲线逐渐下降的趋势正好说明这个能量的转化过程。从图8中看到,球形撞头的动能减小更快,表现在图7中就是球形撞头情况下,双层壳的变形能增加更快。这说明在等量撞深下,双层壳在球形撞头的撞击下吸收了更多的能量。说明在这种情况下,双层壳抵抗球形撞头碰撞的能力更强。
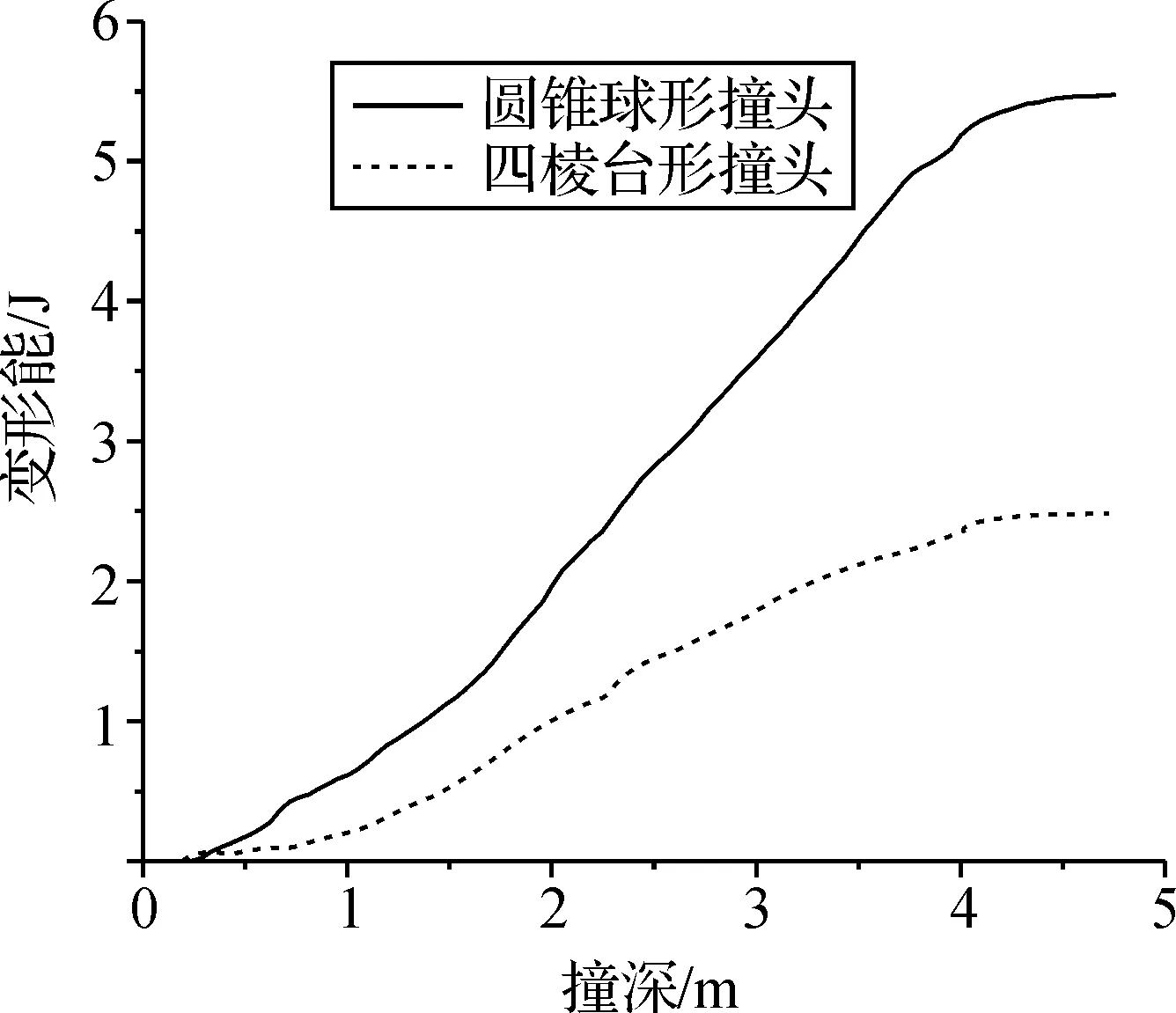
图7 变形能-撞深曲

图8 刚体动能-撞深曲
3 总结
1) 撞头形式的不同导致双层壳结构损伤变形方式有很大的差异,四棱台形撞头更容易引起材料的失效。
2) 等量撞深下,双层壳在球形撞头的撞击下吸收更多的能量,进而得出双层壳结构抵抗球形撞头撞击的能力更强。
以上结论对在船首设计和有限元仿真中合理地近似模拟船首的形状有一定的参考意义。
[1] 王自力, 顾永宁.撞击参数对双层舷侧结构碰撞响应的影响[J].船舶工程, 2000(6):13-16.
[2] Krzysztof Wisniewski, przemyslaw kolakowski.The effect of selected parameters on ship collision results by dynamic FE simulations[J].Finite Elements in Analysis and Design, 2003(39):985-1006.
[3] Kitamura O,.FEM Approach to the Simulation of Collision and Grounding Damage.2ndInternational Conference on Collision and Grounding of Ships[C], Copenhagen, July,2001.
[4] Sajdak J A W, Brown A J.Modeling Longitudinal Damage in Ship Collisions[R].SSC Report SR-1426, 2004.
[5] LS-DYNA KEYWORD USER'S MANUAL[R].USA: Livermore Software Technology Copporation, 2003, Version 970.
[6] 赵海鸥.LS-DYNA动力分析指南[M].北京: 兵器工业出版社, 2001.

