基于MSC.Patran的水翼升力求解方法研究

， ，， ，

(1.江南大学信息工程学院, 江苏 无锡 214122; 2.中国船舶科学研究中心, 江苏 无锡 2140821)

对于水翼船船体，在翼行状态下，船体完全离开水面，船体重量仅由首尾水翼支撑。传统的研究方法需要在不同条件下进行试验，每次试验都需要调整多种参数，如水翼的安装角度和水翼支柱的高度等，准备工作较为繁杂，这就需要找到一种参数化建模的方法，减少手工劳动。

根据水翼升力面理论计算方法，结合大量的水翼试验，中国船舶科学研究中心摸索出一套计算任意平面形状水翼的升力面计算方法，本文在此基础上使用MSC.Patran作为开发和使用平台实现了水翼升力求解方法[1]。

1 原理及求解

高速航行时，水翼在水中前进并获得升力,把船身托出水面,只有水翼、螺旋桨和舵等在水下，系统原理见图1。

图1 系统原理

设一水翼在水面下h浸深，在原为静止的水面下以常数U沿x负方向运动，根据运动转换原理，相当于水翼处于来流速度为U的来流中。o-xyz为固定在静止水面上的右手直角坐标系，自由面为xy平面，z轴垂直向上[2]。

考虑水为不可压缩、无旋、非粘性以及密度均匀的理想流体，则流场中必定存在一扰动速度势函数φ(x,y,z)，在整个流场中满足Laplace方程，即 ：

2φ=0

(1)

总速度势的求解，还需要满足边界条件。

1) 在水翼组合体表面Sb上，扰动速度势φ应满足以下物面边界条件，即速度不穿透物体表面：

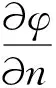
(2)

2) 扰动速度势φ满足远前方无波条件及无限深水中扰动速度为零的条件，即

φ|∞→0

(3)

3) Kutta条件，即在水翼的尾缘处速度为有限值。

|vt,e|<∞

(4)

4) 假定兴波是微幅波，满足线性自由面边界条件，可分为两部分

(1) 运动边界条件：

φ·(y-ζ)=0

(5)

(2) 动力边界条件：

(6)

式中：ζ——自由面波高。

假设平行流速度势为U∞=(U∞,0)，则由式(5)、(6)显性化后得到边界方程：

(7)

根据(6)可以求得自由面波高：

(8)

对于升力绕流问题，尾流可简化成从物面后缘向后泄放的薄涡层，并进一步抽象为无厚度的空间曲面Sw。在此面上允许速度势不连续，但要求在该面两边的法向导数连续。

利用Green定理，满足方程 (1)，(3)，(7)的扰动速度势φ(x,y,z)可表示为：

(9)

利用上述边界条件求得翼形上的偶流强度(速度势)和水面上的源流强度，由这些奇点强度计算翼形上的速度势，然后由速度势沿翼形切线方向的梯度求得切向速度|Vt|，代入Bernoulli方程计算压力P，而各点压力系数CP为：

(10)

则升力系数CL和阻力系数CD为：

(11)

(12)

2 实现过程

水翼升力求解主要有三个步骤，见图2。

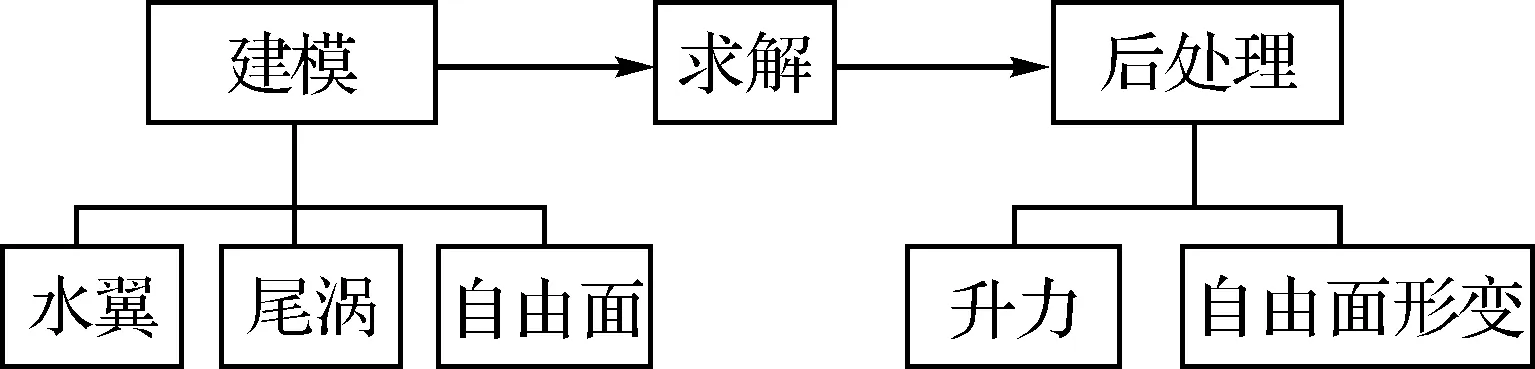
图2 水翼升力求解系统实现过

2.1 参数化建模

经验表明,有限元建模在整个有限元分析中占70% ～80%的工作量[3]。而且在目前的有限元建模中,一般为交互式,如果改变某些参数,就需要重新建模,势必增加工作量。如一个模型有3个参数,每个参数取10个样本,就要建立1 000个模型。这样就不能很好地适应产品设计时的动态特性,影响了设计的自动化程度和设计效率 。在以往的实验中，往往采用两种方法对不同水翼模型结果进行对比，然后择优：(1)模型试验择优，这样需要消耗大量的人力和物力，而且所需要的时间长，不能满足初步设计的要求；(2)理论设计择优，需要重复进行模型建立和网格划分，工作量巨大。

因此，考虑使用关键参数，结合计算机的高效率，将几何建模，模型修改和有限元划分的繁琐工作提交给计算机来完成，集中精力分析得到的数据和结果，选出最优方案。系统以MSC.Patran作为开发平台，使用参数化建模，缩短了整个模型设计的周期，并能根据用户的要求建立不同的模型，方便修改，提高工作效率。

进行参数化建模需要确定模型几何特征参数和有限元特征参数[4]，系统把二者同时作为设计变量,将几何特征参数的作用范围延拓至有限元模型，使有限元模型根据参数变化而变化，实现有限元模型的参数化。见图3所示。

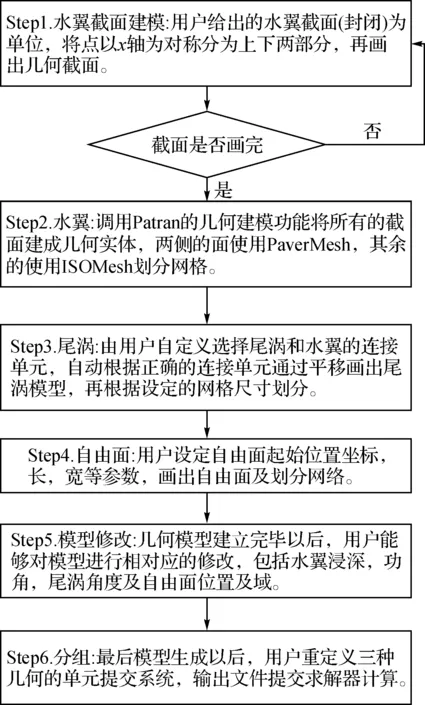
图3 参数化建模流程

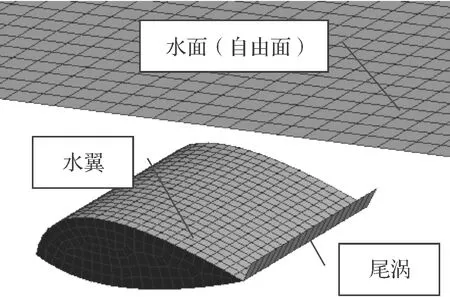
图4 参数化建模的实

2.2 建立工况并求解

建立工况就是测试水翼在各种条件下的状态，每一组工况包括工况名、来流速度vx、vy、vz，高速并非对称。建好的工况将直接保存在db中。

建立工况时，程序使用了PCL的client_data类管理和处理工况数据。client_data类似于数据结构中堆的概念，使用(ID, Client Label, Client Type)方式标识一个数据集合。label在MSC.Patran数据库中数据集合的唯一标识，type是这种数据集合的识别类型，但是对每一个数据集合的存取借助于地址ID完成。如为工况数据的类型和标签定义如下：

#define phases_set_client_type 20

#define phases_set_client_label 2000

则工况数据则从label为2000开始借助下面两个函数存取client_data数据：

get(type, name,n_l, n_i, n_r, n_s, p_l, p_i, p_r, p_s )；

set(type, label_start, name, n_l, n_i, n_r, n_s, p_l, p_i, p_r, p_s )。

一个现有的求解器(*.exe)已经被封装在特定的文件夹内，计算的时候系统把所选择工况对应的参数传入求解器中，然后调用求解器进行计算。最后把计算出来的结果保存在一个*.dat和一个*.plt文件中。为了进行后处理，系统将这两个文件的结果经过数据转换保存到MSC.Patran的数据库中。其中从*.dat文件中获得阻力系数、总面积、升力系数和总投影面积，而从*.plt中获得自由面所有节点在计算前后发生的位移。

2.3 后处理

求解结束后，将保存在db中的数据在MSC.Patran中进行后处理[5]，生成云图、算出自由面形变以及显示升力大小。

系统在求解得到的*.plt文件中取出位移后的点坐标，然后根据初始坐标计算出自由面中所有点的位移，得到自由面的形变，并保存到结果工况中，最后在Patran中显示出来。

3 水翼升力求解数值计算及结果分析

3.1 算例一数值计算及结论

使用参数化建模，创建一块平板水翼，通过不同浸深和功角，求解出升力系数和自由面波峰，得出定性结论，通过专业人员验证，结论正确，证明该方法的有效性。以下是建模的主要参数：

水翼 单截面，网格尺寸0.5；

尾涡 尾涡长度1.0；

自由面 起始位置[0 0 0]，长度(x方向)10，宽度(y方向)4，网格尺寸0.5；

工况参数 来流速度vx：5.0,vy:0,vz:0.0, 非对称：False。极高速：False。

表1表明，当水翼浸深h增大时，对自由面形变影响减小；当攻角变大时，影响增大。

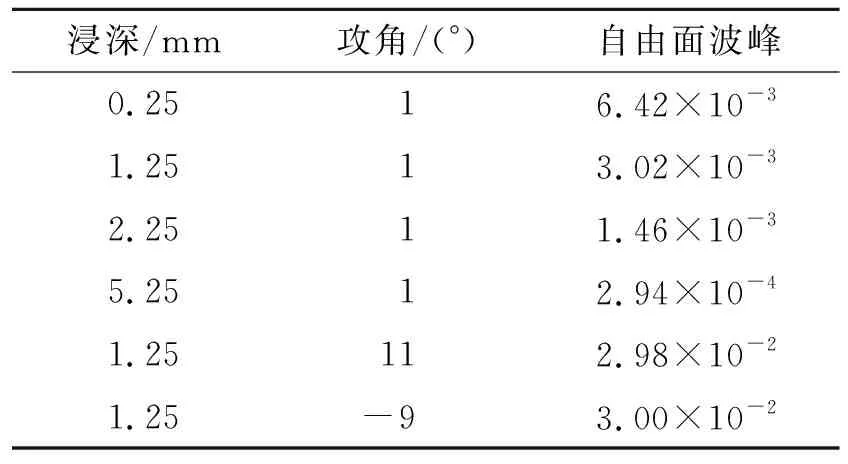
表1 不同浸深和尾涡角度的自由面波峰值

表2表明，当水翼浸深增大时，对升力影响不大；当攻角增大时，升力增大；当攻角为负时，升力也为负。

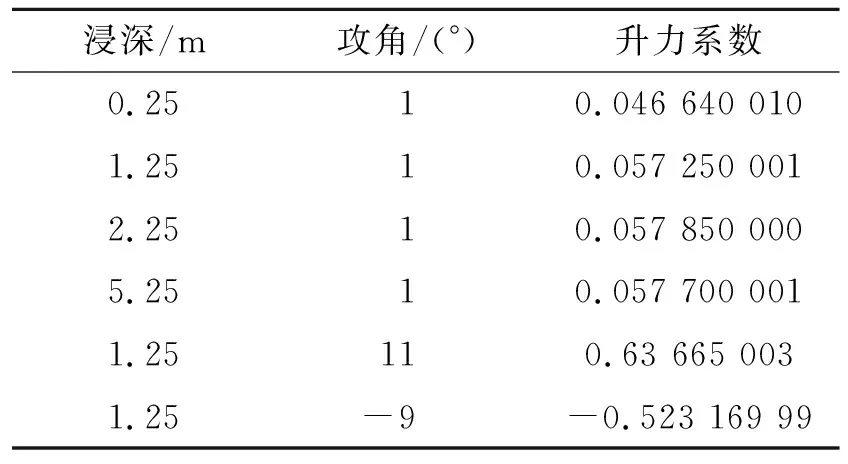
表2 不同浸深和尾涡角度的升力系数

3.2 算例二数值计算及实验

使用NACA4412水翼作为计算算例，对于不同水翼浸深和功角得出的计算结果与实验结果进行比较。证明系统的正确性。

图5是实验模型中水翼和建模完成后的示意图，工况参数见4.1。

图5 试验水翼及自动建模后模型示意

弦长c弗劳德数Frc越小，即来流速度越小。

表3 水翼功角0°时不同浸深的实验和计算对比

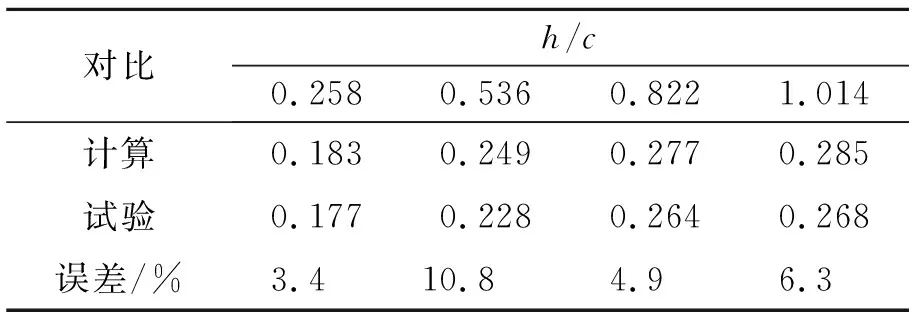
表4 水翼功角4°时不同浸深的实验和计算对比

系统经过求解器计算，可以生成一个*.plt的文件，h/c=0.5，Frc分别为0.5、1.0、2.5和4.5时用TecPlot查看的结果见图6。

a) Frc=0.5

b) Frc=1.0

c) Frc=2.5

d) Frc=2.5

4 总结

文中依据水翼升力面理论计算方法，并对已有的水翼特性经验公式进行整理，在MSC.Patran平台上实现了水翼升力求解的有限元方法，根据水翼模型和流场计算域特征进行参数化建模，改变水翼浸深和尾涡角度得到一系列的实验结果，通过结果与已有规律的对比，发现是一致的，证明了使用该方法的正确性。工程算例的数值计算与试验结果对比表明该方法可以对水翼升力及其分布进行预报。对产品的快速设计和优化都有重要的参考价值。

[1] 马爱军，周传月，王 旭.Patran和Nastran有限元分析专业教程[M].北京：清华大学出版社，2005.

[2] 赵发明.水翼船水动力性能设计预报软件包[D].无锡：中国船舶科学研究中心，2000.

[3] 张培培,陶 华,顾小锋.CAD/CAE集成中参数化有限元建模的研究[J].现代制造工程，2006(9):2-3.

[4] Grose J G, Marx D A, Kranz M, et al.用MSC.Patran进行参数化设计与分析——一种新功能[C].MSC.Software Corp，MSC.Software中国解决方案论坛，2000：583-589.

[5] 朱 鸣，段云岭.读取MSC.Patran数据库中的有限元信息[C].清华大学水利系，MSC.Software中国解决方案论坛,2000：599-602.