超标横流作用下航道尺度加宽研究及应用

摘要：

支流入汇常导致支流口干流航道局部横流加大，进而影响船舶通航安全。为研究超标横流入汇对干流航道尺度的影响，采用Fortran语言自主开发了平面二维水流数学模型和船舶操纵运动数学模型，对模型的合理性和可靠性进行验证后，通过模拟横流作用下的船舶运动，研究了超标横流对船舶横漂速度和漂角的影响，提出了超标横流安全范围和航道定量加宽值。实例应用表明：在传统航道尺度设计下，当支流口超标横流范围较小时可通过调整舵角实现航行安全；而当超标横流范围较大时则难以保障船舶安全通航，需进行河道加宽设计。提出的超标横流条件下航道加宽确定方法基本合理，对船舶操纵运动和航道设计具有一定参考价值。

关" 键" 词：

超标横流； 航道加宽； 水流数学模型； 船舶操纵运动数学模型； 支流入汇

中图法分类号： U676

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2025.01.021

收稿日期：2024-05-11；接受日期：2024-07-01

基金项目：

国家重点研发计划项目（2018YFE1600400）；广西科技重大专项项目（桂科AA23023009）

作者简介：

陈浩东，男，硕士研究生，主要从事水力学及河流动力学研究。E-mail：2463645090@qq.com

通信作者：

童思陈，男，教授，博士，主要从事水力学及河流动力学研究。E-mail：81441849@qq.com

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2025） 01-0156-08

引用本文：

陈浩东，童思陈，张莹，等.超标横流作用下航道尺度加宽研究及应用

［J］.人民长江，2025，56（1）：156-163.

0" 引 言

中国自然河道中普遍存在着横流现象，只有了解横流对船舶操纵性的影响，才能使船舶在复杂环境条件下做出正确的运动响应，保障船舶航行的安全［1-2］。对于天然河道不同交汇口，汇流比和交汇角作为干支流交汇的主要特征［3-5］，对通航水流条件有决定性影响。王冰洁等［6］利用数值模拟探讨了入汇角为90°的河流交汇处水流特性，并提出了优化整流方案。薛博升等［7］通过45°明渠交汇水槽试验，发现入汇口下游区域流速不均匀程度随汇流比增大而增加。张磊等［8］结合横流、风等条件，构建了大型船舶通过典型航道的允许尺度数学模型。此外船舶在经过桥墩时也会受到横流作用的影响［9-12］，使得船身发生漂移和偏转。刘晓平等［13］重点分析了桥区河段横流对船舶航行的影响，发现影响程度随船舶尺寸增大而减小，与船舶航速成负相关。国内外众多学者通过水槽模型试验、船模试验和数值模拟等方法对弯曲河段［14-15］及引航道［16-18］等区域内的横流特性进行研究，如牛国杰［19］通过水槽模型试验建立了弯曲河段处最大舵角和横向流速与船速比值的计算模型；张羽等［20］对引航道通航水流条件的研究发现，横流随回流漩涡与引航道轴线的夹角增大而增大。此外，针对不同实际工程条件下的支流入汇及其产生的横流对船舶航行的影响，多位学者通过建立二维、三维模型对干支流交汇河段的横流特性进行计算分析［21-23］。

但同时可以看到，以往学者主要研究横流较小情况下的船舶通航，鲜见超标横流对船舶通航条件的影响研究。为此，本文采用Fortran语言编程船舶操纵运动数学模型，探讨了干支流交汇区超标横流条件下的航道加宽确定方法，以为干支流交汇航道设计提供参考。

1" 平面二维水流数学模型及船舶操纵运动数学模型构建

1.1" 基本方程

为分析自然河道水流运动特性，考虑到河道蜿蜒曲折、边界波动较为明显等因素，本文采用平均水深有限元法建立二维水流数学模型。

船舶运动一般具有6个自由度。鉴于本文重点研究平面内的船舶运动，因此采用直角坐标系x0Oy0，主要研究船舶在平面内三自由度运动（图1）。

船体在平面内的三自由度运动可根据牛顿第二定律来描述，具体方程如下：

X0=mx0GY0=my0GN=IZψ（1）

式中：X0、Y0分别为作用于船x0轴和y0轴方向上的合力；N为绕船重心垂直轴的合力矩；m为船舶质量；ψ为艏向角；x0G、y0G分别为t0时刻船舶重心G的横坐标和纵坐标；Iz为绕z轴船的质量惯性矩。

1.2" 水动力表达式

常用的水动力模型将X、Y、N表达为

X=XH（vx，vy，r）+XR（vx，vy，r）+XP（vx，vy，r）+XW+XWVY=YH（vx，vy，r）+YR（vx，vy，r）+YP（vx，vy，r）+YW+YWVN=NH（vx，vy，r）+NR（vx，vy，r）+NP（vx，vy，r）+NW+NWV（2）

式中：下标W、WV分别表示风和波浪的作用；H、R、P分别表示裸船体、舵、螺旋桨。

1.3" 船舶操纵运动方程的求解

船舶操纵运动方程是具有一阶导数的常微分方程组，求解十分复杂，而龙格-库塔法可以有效求解一阶导数的常微分方程组。实际工程应用中考虑计算的稳定性和精度，可采用四阶格式计算出船舶操纵运动方程的数值解，得到船舶任意时刻的位置和相关参数离散方程：

xi+1=xi+（uxicosψi-uyisinψi）Δtyi+1=yi+（uxisinψi+uyicosψi）Δtψi+1=ψi+riΔtvx，i+1=ux，i+1-VFcos（ψF-ψi+1）vy，i+1=uy，i+1-VFsin（ψF-ψi+1）（3）

式中：xi、yi分别为船舶在i时刻的横向和纵向位置；uxi、uyi分别为船舶在i时刻横向和纵向的对岸航速；ψi为船舶在i时刻的艏向角；ri为船舶在i时刻的转首角速度；Δt为离散时间步长；VF、ψF分别为固定坐标系中水流的绝对速度和方向； vx，i+1、vy，i+1为船舶在i+1时刻船体与水流的相对速度。

2" 数学模型验证

2.1" 二维水流数学模型验证

本文选取长江干流长寿扇沱河段进行数模验证。验证河段为自东向东北过渡的弯道段，计算域为两蟾堆上游6.0 km，到桥段下游4.0 km，流量Q=4 280 m3/s。图2～3分别为水位与流速的验证关系，水位误差控制在±0.04 m的范围内，流速偏差控制在±0.05 m/s以内，表明模拟结果与实际测量结果相符。

2.2" 船舶操纵运动数学模型验证

本文选取内河航道代表船型（表1）分别计算静水直线航行和静水旋回性能（图4）。模拟结果表明，代表船舶静水直航性能稳定，直线航行航速、航行的轨迹线以及航行方向均合理。在静水条件下，操纵舵角达到25°时代表船舶的回转直径D大约是其船长的2倍，满足定常回转直径约为1.5～3.5倍船长的要求，说明船舶操纵运动计算的内河航运货船直航推进性能和静水回转性能稳定。

2.3" 船舶操纵性试验仿真

为进一步检验船舶性能，在静水条件下进行船舶满舵回转运动（图5）和不同舵角的“Z”形试验仿真（图6～7）。结果表明，模拟值和实际值较为吻合，说明船舶操纵运动模型可以较好地模拟实际船舶操纵运动；船舶的“Z”形运动呈周期性变化，舵角越大，完成一个周期的运动距离越小，船舶运动轨迹偏离中心线的距离越大。

3" 超标横流对船舶航行影响分析

3.1" 超标横流对船舶横漂的影响

内河航道中，船舶航行受到横向水流和舵角的影响，会导致船舶产生横向漂移，船舶横向漂移的速度即为横漂速度，是评价横流对船舶航行影响的重要指标之一。横漂速度主要与横向流速、航道等级和船型参数相关，横流速度越大，横漂速度越大（图8），本次模拟中，假定船舶对岸航道Vs=0.5 m/s［24］。

3.2" 超标横流对漂角的影响

根据GB 50139—2014《内河通航标准》［1］规定，不同航道等级对航行漂角有不同要求，Ⅰ～Ⅲ级航道中，船舶或船队的航行漂角应取3°，而在Ⅳ～Ⅴ级航道中则应取2°。通过模拟不同超标横流条件下的船舶运动，研究超标横流对船舶航行漂角的影响（图9）。模拟结果显示，在同一航道等级中，横流速度越大，漂角越大；对于不同航道，相同横流条件下，航道等级越高，漂角越大。

3.3" 超标横流条件下航道范围限值

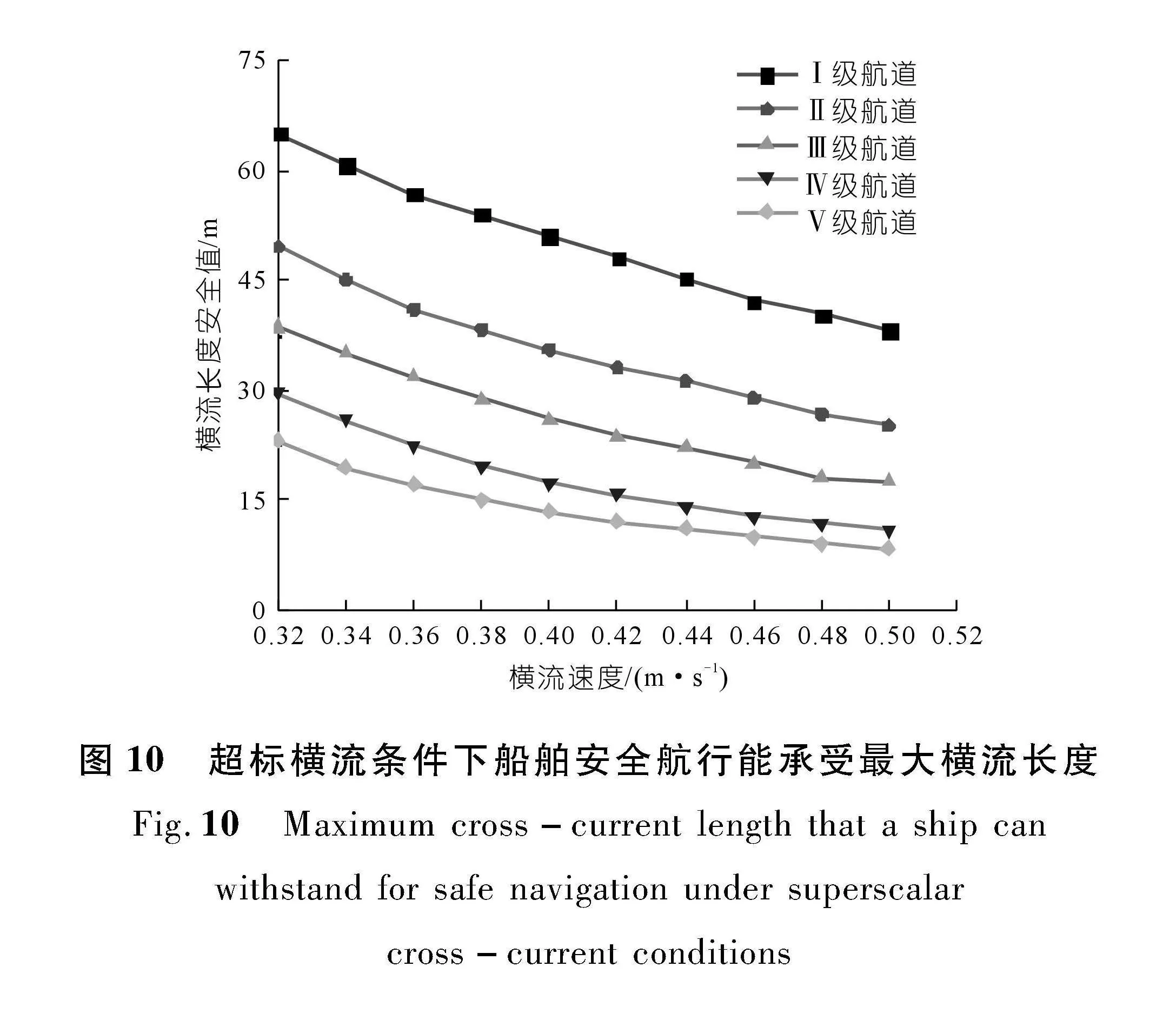
为探讨超标横流条件下船舶安全航行的最大范围，假定超标横流宽度为单线航道宽度，流速为3.0 m/s，船舶对岸航速为0.5 m/s，航行舵角为25°。模拟不同超标横流范围内船舶航行状态，得到超标横流条件下船舶安全航行能承受的最大横流范围（表2、图10）。

由图10可知，同一航道等级下，超标横流速度越大，船舶安全航行能承受范围越小；而在同一超标横流速度情况下，航道等级越高，所需横流长度安全值越大。

3.4" 超标横流条件下所需航道加宽值

为研究超标横流条件下航道加宽值，通过模拟不同航道等级、不同横流条件下代表船舶的航行过程，探讨超标横流与航道尺度的关系。设满载3 000 t货船在均匀横流区域航行，航宽100 m，船舶对岸航速0.5 m/s，Vy为横流速度，可模拟得到代表船舶在横流分布区域的航行极限状态和关键参数，确定各级航道超标横流范围与横漂距离关系。综合分析不同横流条件下各级航道的航宽增加值，得到超标横流条件下各级航道加宽值如图11所示（限于篇幅，图中仅给出了Vy=0.4，0.5 m/s的情况）。

由图11可知，相同条件下，超标横流范围越大，各级航道加宽值越大；航道等级越高，航道加宽值越小，相邻等级的航道加宽值差值越小。这是因为航道等级越高，航道越宽，代表船舶的吨级越大，船舶受横流作用影响越小，船舶的横向漂移量越小，所需航道加宽值也越小。

4" 超标横流作用下典型河段航道尺度确定

4.1" 典型河段概况

平陆运河沿线支流众多，支流汇入运河后干流航道存在不同程度的横流影响。本文选取沙埠江和广平河两条重要支流口进行研究，探讨支流口超标横流与航道尺度的关系。以内河航道3 000 t级货船为代表船舶，选取最不利通航水文组合（即运河干流5 a一遇洪水+支流20 a一遇洪水）进行模拟。

4.2" 船舶操纵运动仿真

4.2.1" 沙埠江支流口船舶操纵运动数值模拟

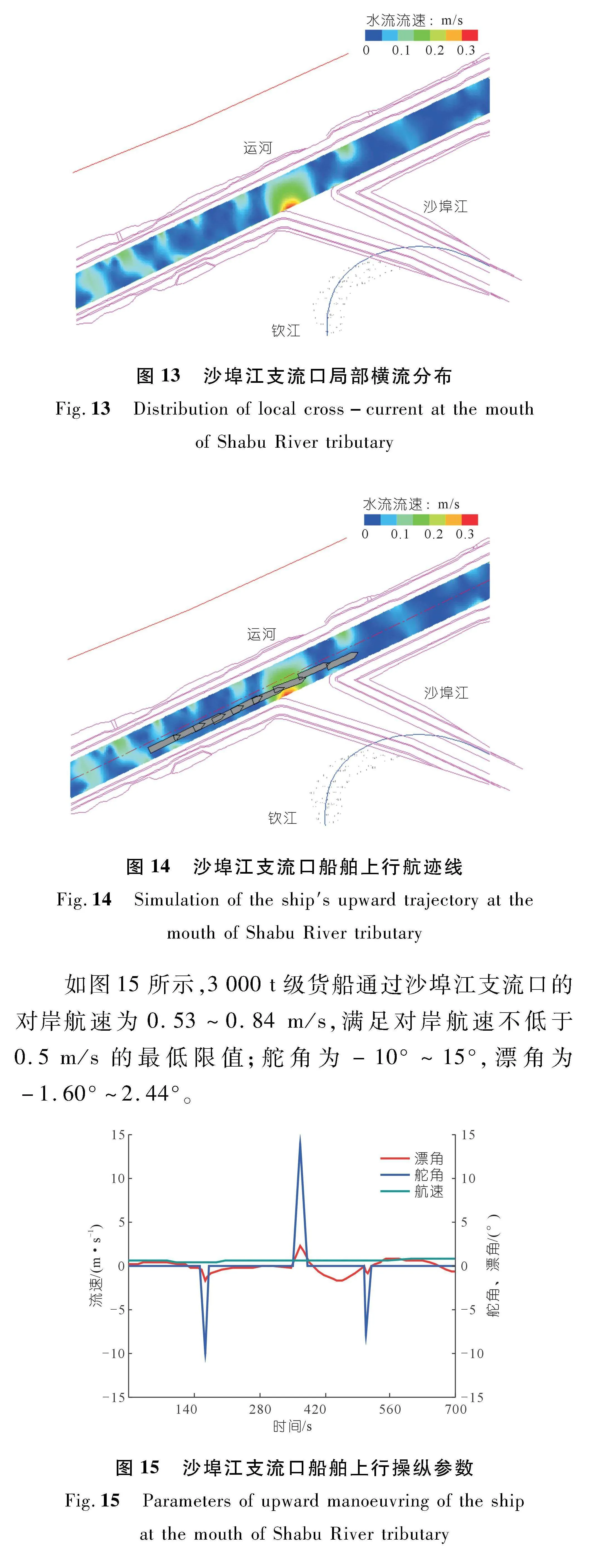
通过平面二维水流数学模型计算，沙埠江支流口航道横流速度为0～0.35 m/s，沙埠江超标横流范围相对较小，约45.0×20.0 m（长×宽），最大横流速度约0.35 m/s，已超过标准限值0.3 m/s，如图12～13所示。

结合沙埠江支流口航道内的实际流场分布进行船舶运动仿真，设置船舶初始航速为2 m/s，初始航向角为67°（规定正北方向和船艏方向的夹角为船舶的航向角，以顺时针方向为正），初始舵角为0°，航行时间为700 s，仿真结果见图14。

如图15所示，3 000 t级货船通过沙埠江支流口的对岸航速为0.53～0.84 m/s，满足对岸航速不低于0.5 m/s的最低限值；舵角为-10°～15°，漂角为-1.60°～2.44°。

模拟结果显示，沙埠江支流口横向流速虽然超标，但超标横流数值和范围较小，横流对船舶航行的影响作用相对较小，可通过调整船舶舵角实现航行安全，无需对航道进行加宽设计。

4.2.2" 广平河支流口船舶操纵运动数值模拟

根据平面二维水流数学模型模拟计算，广平河支流口航道横流速度约0～0.50 m/s，超标横流范围相对较大，范围约80.0 m×58.0 m（长×宽），最大横流速度约0.50 m/s（图16）。

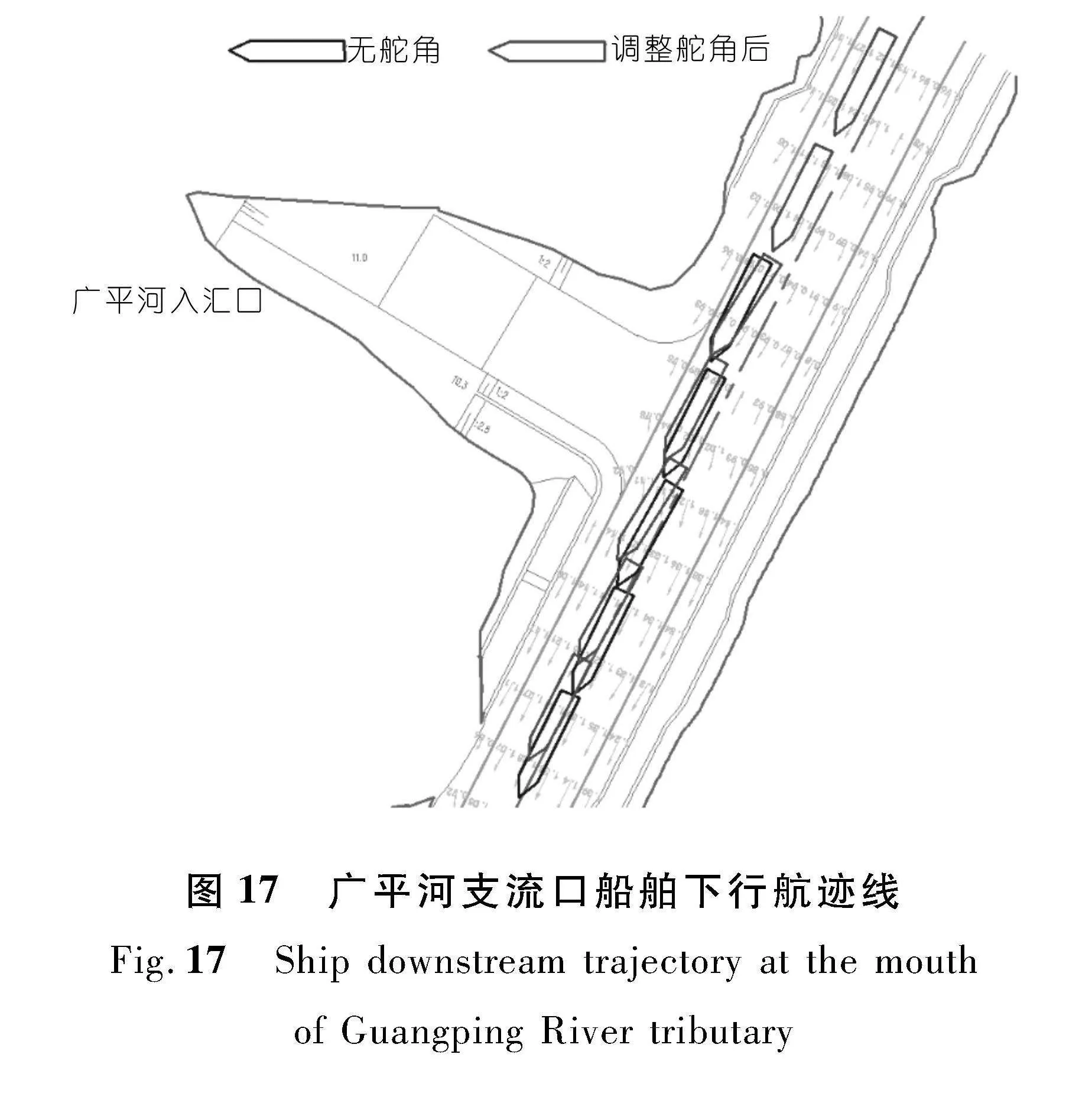
基于广平河支流入汇口航道内的实际流场分布，发现超标横流主要分布在航道右岸（图16）。横流对上行船舶影响较弱，因此结合航道规划确定船舶航线向下航行，采用船舶操纵运动数学模型进行船舶运动仿真（图17），设置船舶初始航速为2 m/s，初始航向角为207°，初始舵角为0°，航行时间为300 s。

由图18可知，代表船舶通过广平河支流口的对岸航速为1.58～2.00 m/s，舵角为-25°～25°，漂角为-15°～20°。可以看出，由于支流入汇口航道内超标横流以及超标横流分布范围较大，即使船舶调整舵角达到最大值25°，也难以克服横流对船舶航行的影响，导致船舶偏离航道中心线，影响船舶通航安全。对此，需要对航道进行加宽设计。

4.2.3" 航道加宽后船舶操纵效果

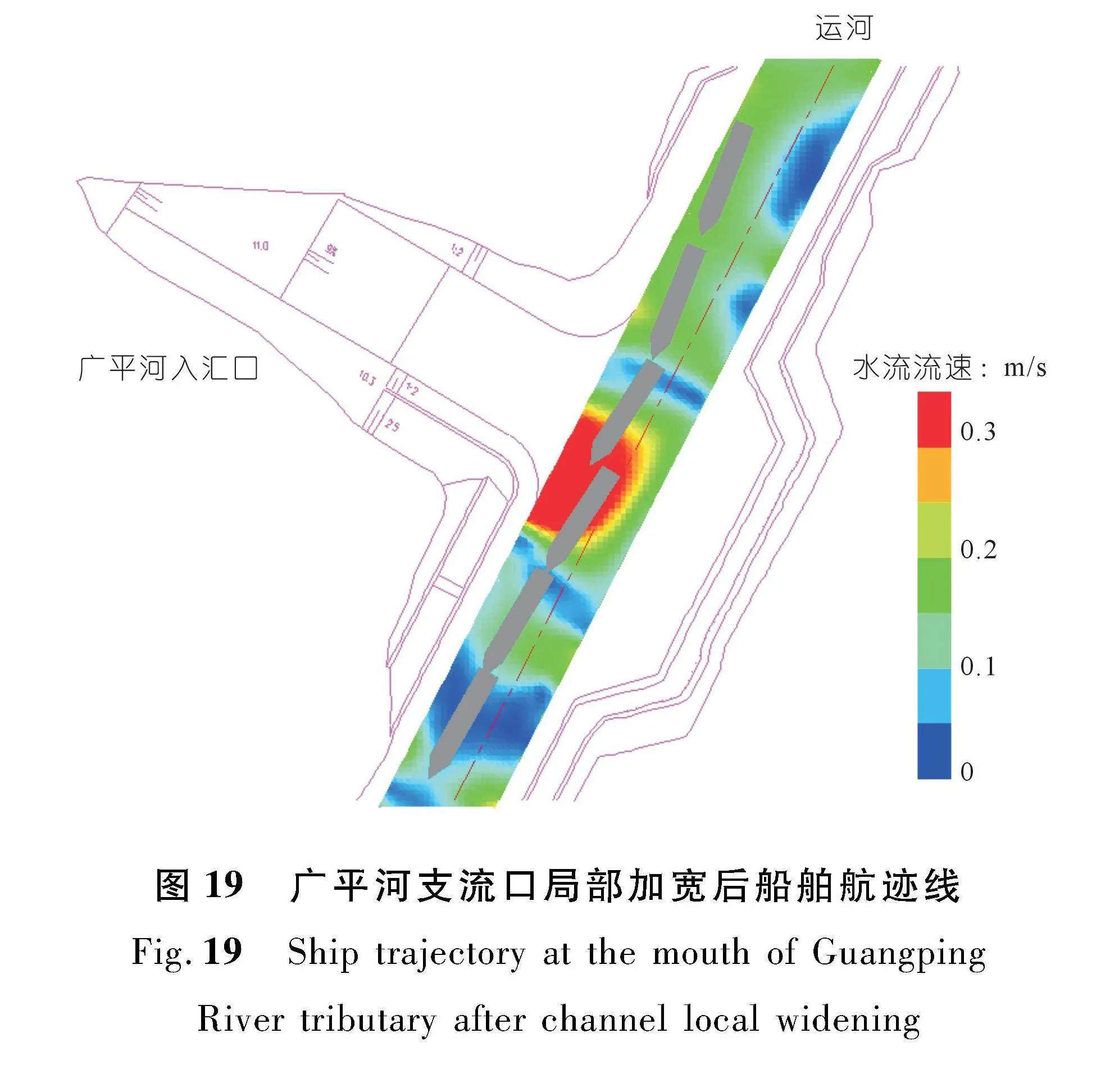
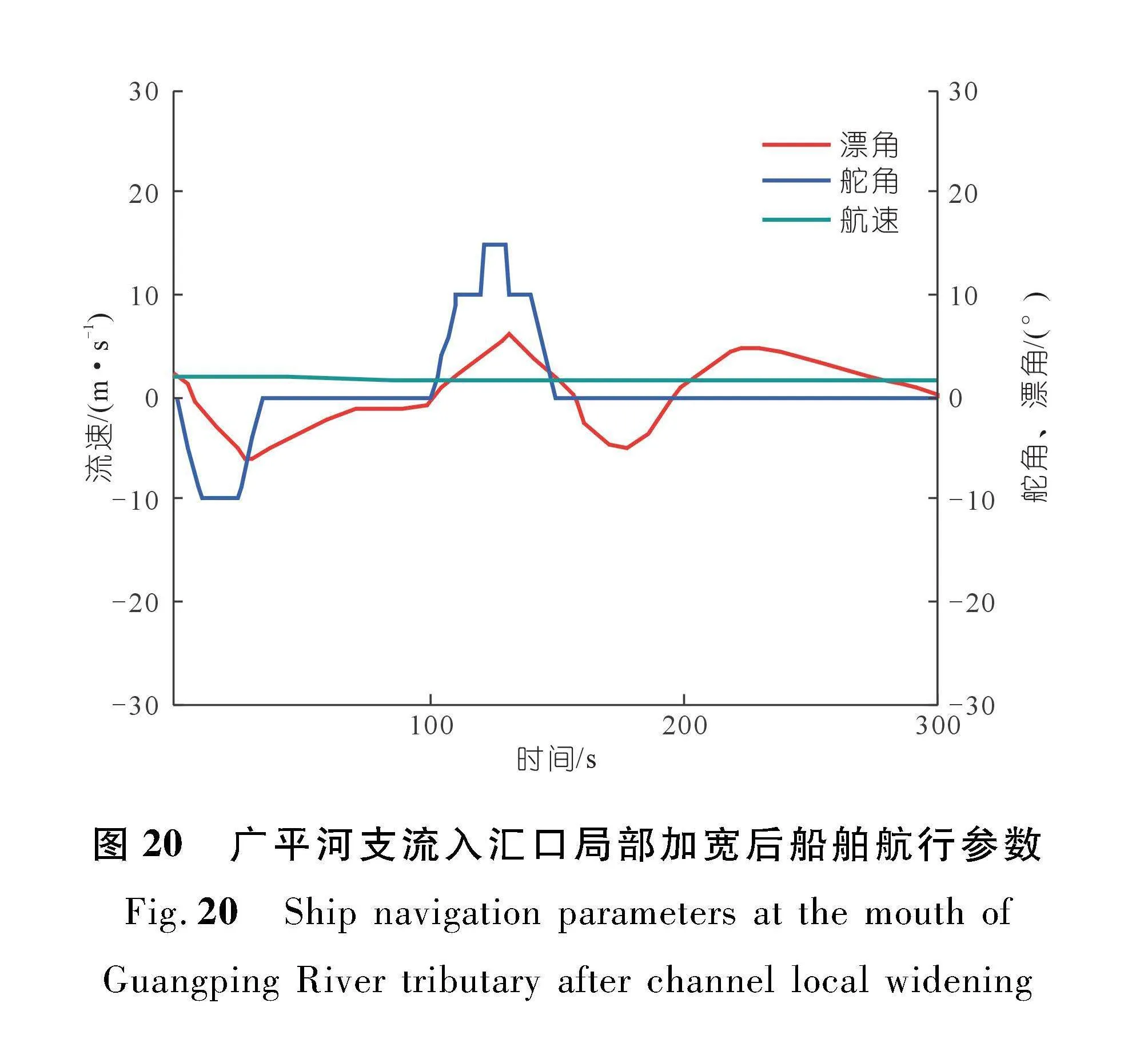
由于广平河支流口航道内超标横流范围较大，达80.0×58.0 m（长×宽），超标横流平均值为0.4 m/s。为保证通航安全，根据航道加宽值研究结果，将横流超标区域的航道局部加宽48 m，加宽后船舶操纵仿真结果如图19所示，船舶的航行参数见图20。广平河支流口航道局部加宽后，代表船舶通过该河段的对岸航速为1.61～2.00 m/s，舵角为-10°～15°，漂角为-7°～5°，船舶受超标横流影响的区域减小，可实现安全通航。

5" 结 论

（1） 通过Fortran语言编程，从底层自主开发了平面二维水流数学模型和船舶操纵运动数学模型，对典型河段进行了水流数值模拟，并对船舶静水直航、旋回运动以及“Z”形试验进行了模拟及检验，验证了二维水流数学模型以及船舶操纵运动数学模型的合理性。

（2） 基于平面二维水流数学模型和船舶操纵运动数学模型，模拟分析了超标横流对船舶航行和航道尺度的影响。结果显示，同一航道等级情况下，横向流速越大，横漂速度越大，漂角越大，所需航道加宽值越大；相同横流条件下，航道等级越高，航道加宽值越小。

（3） 选用两条典型支流口入汇河段，对超标横流条件下的航道加宽情况进行了船舶操纵运动模拟。结果显示，当超标横流数值和范围较小时，船舶仍可安全通行；但当超标横流数值和范围较大时，则需要对航道尺度进行加宽设计，以确保船舶的航行安全。

参考文献：

［1］" 中华人民共和国住房和城乡建设部.内河通航标准：GB 50139—2014［S］.北京：中国计划出版社，2015.

［2］" 张钟.船舶交汇水域通航安全管理［J］.世界海运，2023，46（10）：6-11.

［3］" 曹凌瑞.支流入汇对干流航道通航影响研究［D］.长沙：长沙理工大学，2022.

［4］" 刘倩颖.长江上游干支流汇合口水沙特性研究［D］.重庆：重庆交通大学，2011.

［5］" 李慧.掺混模式对河流交汇区水流混合动力特性的影响研究［J］.水利水电快报，2023，44（2）：1.

［6］" 王冰洁，周苏芬，王海周，等.明渠干支河流直角交汇区整流方法探讨［J］.四川大学学报（工程科学版），2015，47（增1）：7-12.

［7］" 薛博升，魏炳乾，王非，等.汇流比和入汇角对明渠交汇水流特性影响的对比研究［J］.应用力学学报，2019，36（3）：658-665，762，763.

［8］" 张磊，陈爽，刘明俊，等.长江干线航道通过大型船舶尺度研究［J］.武汉理工大学学报，2024，46（1）：112-120.

［9］" GENG Y F，GUO M Y，GUO H Q，et al.Safety range in bridge areas based on the influence of cross flow on ship navigation［J］.Ocean Engineering，2023，281：142-156.

［10］魏彭林.山区河流桥墩紊流宽度确定及横流取值研究［D］.重庆：重庆交通大学，2017.

［11］余葵，吴威力，刘宪庆，等.山区涉河桥墩布设防撞装置对通航的影响［J］.水运工程，2022（6）：119-126.

［12］柯兴.航道桥区段水流通航影响研究［D］.南京：东南大学，2020.

［13］刘晓平，李明，方松森，等.桥区河段横流对船舶航行的影响［J］.水利水运工程学报，2012（2）：21-26.

［14］YANG X，WANG X.A combined numerical-experimental approach to analyze cross flow problems in the entrance channel：a case study of Lanshan Port，China［J］.Ocean Engineering，2017，146：401-410.

［15］刘杨，冯君，胡世良，等.航速、横流对艏侧推侧向力的影响［J］.江苏科技信息，2019，36（32）：38-43.

［16］MOHAMED S M，MOHAMED M A M，GAMAL E H，et al.Effect of cross water currents on a representative navigational ship in Egypt［J］.International Journal of Academic Research，2013，5（4）：278-289.

［17］YAN T，QIAN D G，SHU Y Q，et al.Vessel navigation risk and stern-swing index in sharp bend channels［J］.Ocean Engineering，2021，238：142-159.

［18］肖鑫，曹凤帅.引航道内船舶安全通航影响因素浅析［J］.中国水运（下半月），2017，17（3）：22-23，25.

［19］牛国杰.弯曲河段船闸口门区通航水流条件限值的研究［D］.长沙：长沙理工大学，2020.

［20］张羽，杨朝辉，赵集云，等.弯曲河段船闸引航道通航水流条件模拟［J］.水运工程，2022（6）：132-138.

［21］李乔.河道交汇水流对船舶操纵性的影响研究［D］.重庆：重庆交通大学，2019

［22］杨晓红，周杨，顾春雨.水流流动对交叉河流汇流区通航性能影响分析［J］.中国水运（下半月），2017，17（1）：20-22.

［23］余葵，杨小岳，张聪，等.高速横流作用下内河船舶偏转状态研究［J］.水利与建筑工程学报，2023，21（1）：186-192.

［24］周冠伦.航道工程手册［M］.北京：人民交通出版社，2003.

（编辑：胡旭东）

Determination of channel scale widening and application under excessive transverse flow effect

CHEN Haodong1，2，TONG Sichen1，2，ZHANG Ying3，SUN Kai4，WANG Xiang1，2

（1.School of River and Ocean Engineering，Chongqing Jiaotong University，Chongqing 400074，China；

2.National Engineering Research Center for Inland Waterway Regulation，Chongqing Jiaotong University，Chongqing 400074，China；

3.Water Resources Bureau of Bishan District，Chongqing City，Chongqing 402760，China；

4.Wujiangdu Power Plant，Guizhou Wujiang Hydropower Development Co.，Ltd.，Guizhou 563104，China）

Abstract：

The confluence of tributaries often leads to the increase of local transverse flow in main channels，which affects the navigation safety.In order to study the influence of excessive transverse flow on the channel scale of the main stream，one two-dimensional flow mathematical model and a ship maneuvering motion model were developed independently by Fortran language.After the rationality and reliability of the model were proved，the influence of excessive transverse flow on the transverse drift velocity and drift angle of ship navigation was studied by simulating the ship motion under the action of excessive transverse flow，the safety range of excessive transverse flow and the quantitative widening value of the channel were proposed.The practical application showed that under the traditional channel scale design，when the excessive transverse flow at the estuary is contained in a limited range，the navigation safety can be realized by adjusting the rudder angle；while the excessive transverse flow range is large，it is difficult to ensure the safe navigation of ships，so the river channel is required to widen.The determination method of channel widening proposed in this paper is basically reasonable，which has certain reference values for ship maneuvering motion and channel design.

Key words：

excessive transverse flow； channel widening； flow mathematical model； ship maneuvering motion model； inflow of tributary