基于灰色马尔科夫模型的青岛市港口物流需求预测

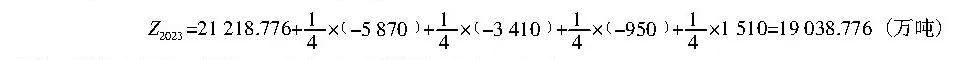
摘" 要：商品流通是经济发展的重要过程，在经济全球化的今天，港口成为一种重要资源。港口货物吞吐量的精确预测可以为港口建设规划提供重要依据。文章结合灰色预测理论和马尔科夫链理论，构建了灰色马尔科夫预测模型，以青岛市2002—2021年的港口货物吞吐量为原始数据，分别使用传统GM1，1模型和灰色马尔科夫模型进行预测，结果分析表明马尔科夫优化的灰色模型预测精度较高，并以此预测了青岛港接下来五年的物流需求数据。根据2022—2026年青岛港货物吞吐量预测结果，青岛港物流增长很快，发展空间很大。

关键词：灰色预测；马尔科夫链；港口物流；物流需求

" 中图分类号：U691" " 文献标志码：A

DOI：10.13714/j.cnki.1002-3100.2025.03.004

Abstract： Commodity circulation is an important process of economic development， in economic globalization of today， the port has become an important resource. Accurate prediction of port cargo throughput can provide an important basis for port construction planning. Based on the grey prediction theory and Markov chain theory， this paper constructs a grey Markov forecasting model， which is based on the raw data of Qingdao's cargo throughout from 2002 to 2021， the traditional GM1，1 model and grey Markov model were used to predict the model respectively. The results showed that the grey model optimized by Markov had higher prediction accuracy， and used it to forecast Qingdao Port's logistics demand data for the next five years. According to the 2022 to 2026 cargo throughput forecast results Qingdao Port logistics growth is very fast， the development space is very big.

Key words： grey forecast; Markov chain; port logistics; logistics demand

0" 引" 言

港口是水路和陆运两种运输方式的交叉点，在物流体系中非常特殊。经济一体化打破了港口独立发展的局势，港口也成为全球经济大循环体系的重要节点，其地位由普通的物流转运站向综合服务中心改变。青岛市政府发布的《青岛市“十四五”物流业发展规划》明确提出要将青岛港打造成世界一流的海洋港口。青岛港地理位置优越，对内可以运输山东、山西的各种矿物、海产品、农副产品等，为我国的西部大开发提供丰富的资源和技术支持；对外，是世界第五大港口，是我国北部海岸的海上门户，对世界经济大循环具有重要作用。查阅统计局数据，青岛港2021年港口货物吞吐量达63 029万吨，比2020年增长了2 570万吨，发展潜力非常大。通过预测青岛港未来的货物吞吐量，可以前瞻性地把握港口吞吐量的发展趋势，并提前规划港口发展方向、泊位位置、港口经营策略和基础设施投资规模等方面，避免港口基础设施建设过度和资源闲置浪费。综上所述，物流吞吐量预测对港口决策非常重要。

1" 文献综述

当前，港口物流需求预测多采用定量分析的方法，即运用统计方法、数学模型等手段，对港口未来发展规模、水平进行预测。根据方法的不同，港口吞吐量的定量预测方法可分为单项预测和组合预测[1]。有些学者使用一种模型进行预测，如陈治霖等[2]考虑到疫情对航运业务的影响，建立SARIMA模型预测了上海港的集装箱吞吐量；Farhan et al.[3]提出了一种系统的方法利用SARIMA模型来预测全球20个主要港口的短期集装箱吞吐量和季节性变化，可以有效运用于季节变化的预测；Patil et al.[4]分别利用单变量和多变量的时间序列回归模型对孟买港口的货运需求进行了预测，证明多变量模型效果更优；Gargari et al.[5]分别用SARIMA和NN模型预测了港口集装箱运输量，证明在预测集装箱运输量时，神经网络模型优于SARIMA模型；陈雄寅[6]在使用Pearson分析指标相关性的基础上，构建了BP神经网络模型，通过对比，发现BP神经网络模型预测精度优于多元线性回归模型；孙晓聪等[7]提出了一种基于随机森林理论的双向长短记忆网络模型，比较预测结果，发现RF-双向LSTM模型预测精度高于RF-LSTM和BP神经网络模型。

另一部分学者使用由多种模型构成的组合模型进行预测，蔡婉贞等[8]利用了BP神经网络和RBF神经网络对汕头港物流需求进行预测，最后构建了组合预测模型；Jiao et al.[9]构建了基于灰色GM1，1模型和RBF神经网络模型的组合预测模型，证明灰色RBF神经网络可以提高货运量预测精度；赵龙文等[10]将季节自回归移动平均模型和BP神经网络模型的预测结果进行整合，对港口船舶的交通流量进行了预测；Huang[11]构建了基于三阶指数平滑、Logistic生长曲线以及BP神经网络三种模型的组合预测模型，验证了组合模型预测更精确；王向前等[12]考虑货物吞吐量受多方面影响，将ARIMAX和支持向量回归预测模型的优点结合，构建了组合模型；邓萍等[13]建立了支持向量回归模型和基于分数累加理论的FGM1，1模型，并使用IOWA算子赋权来进行组合预测。

" 从上述文献可知，组合预测的预测精度通常高于单项预测，在单项预测的基础上进行改进也能提高预测精确度。考虑到灰色预测在短期预测方面的优势，本文选择利用马尔科夫理论优化的灰色预测模型来预测青岛港物流需求。

2" 研究方法

2.1" 灰色GM1，1模型

灰色预测模型主要研究数据量较少的不确定性系统。因为数据的数量较少，想找出系统的发展演变规律很困难，所以学者们研究小数据预测的重点是模型的有效性和可靠性。研究中，通常利用降低模型数据的随机性来保证小数据系统预测结果可靠。灰色预测法主要通过累加原始数据来降低预测数据的随机性。序列累加生成可以将灰色过程由灰变为白，在灰色理论中起着非常重要的作用。通过序列累加生成，可以看到灰量积累过程的发展趋势，从而将零碎的原始数据中所隐藏的特征或规律完全展现出来。一般情况下，在累加过程中，非负数列的变化都是单调增加的。所以，可以利用单调函数来拟合这一增长趋势，并在此基础上构建相应数学模型。

应用中GM1，1是最简便的一种方法。它对原始数据要求低，使用一阶线性微分方程计算也不复杂，因此其适应性强，结果也比较可靠。建模过程如下：

（1）设港口货物吞吐量的原始数列为：

X=Xi， i=1，2，…，n" " " " " " " " " " " " " " " " " " " " （1）

（2）对X进行一次累加处理，生成数列X：

令X1=X1， X2=X2+X1， …， Xn=Xn+Xn-1，得累加序列：

X=Xk， k=1，2，…，n" " " " " " " " " " " " " " " " " " " " （2）

（3）计算X的紧邻均值Z：

Zk=Xk-1+Xk" " k=2，3，…，n" " " " " " " " " " " " " " " （3）

（4）确定累加矩阵B以及常数项Y：

B=" " Y=" " " " " " " " " " " " " " " " " nbsp;（4）

（5）建立X的微分方程：

+aX=u" " " " " " " " " " " " " " " " " " " " " " "（5）

（6）因为B、Y已知，求解灰参数：

=a，u=BBBY" " " " " " " " " " " " " " " " " " " " " （6）

（7）将a、u代入公式（5）得：

k+1=X1-e+， k=1，2，…，n" " " " " " " " " " " " " " " "（7）

（8）进行递减还原，得到预测结果：

k+1=k+1-k" " " " " " " " " " " " " " " " " " " （8）

2.2" 灰色马尔科夫模型

马尔科夫模型认为时间序列是一种随机过程，通过分析事物各状态的初始概率以及转移到其他状态的概率，可以确定事物的发展趋势。马尔科夫预测的最大特征是没有滞后，也就是过去的状态不对预测的未来状态产生影响，预测结果只与当前状态有关，这一特性正好弥补了灰色预测在预测波动较大的数据时准确性较低的缺陷。所以结合灰色预测模型和马尔科夫理论，利用马尔科夫修正灰色GM1，1模型的残差，可以提高预测的精确度。具体建模过程如下：

（1）状态区间划分

" 计算出原始数据和灰色预测结果的残差，明确残差的范围区间。分析残差区间和样本数量，划分出n个状态区间，区间表示为：

E=e，e" " i=1，2，…，n" " " " " " " " " " " " " " " " " " " " （9）

（2）建立状态转移矩阵P

" 当残差属于区间E时，认为事件处于状态E。同理，可能状态还有E、E、…、E。事件从E状态转移到E状态的概率为P，将所有的转移概率构建出一个矩形，即：

P=" " " " " " " " " " " " " " " " " " " " " "（10）

（3）计算预测值

" 以某一年的状态可以通过状态转移矩阵预测下一年的状态，模型可表示为：

P=P*P" " " " " " " " " " " " " " " " " " " " " " " "（11）

式中：P为状态转移矩阵， P为t 时刻的状态概率向量，通过P和P可以计算得到t+1时刻的状态概率向量P。P为t+1时刻相对误差所在各个区间状态的概率，取残差区间的中间值计算得出马尔科夫修正值，与灰色预测值结合得灰色马尔科夫模型预测结果。

3" 实证分析

3.1" 数据来源

本文实验数据来源于《2022年青岛统计年鉴》，为保证数据有效性，选取了2002—2021年这20年间的青岛市港口货物吞吐量为原始数据，如表1所示。

3.2" 灰色GM1，1预测

（1）确定原始数据序列：

X={12 252， 14 135， 16 303， 18 727， 18 727， 26 507， 30 029， 31 668， 31 668， 37 971， 37 971， 45 782， 47 701， 49 749， 51 463， 51 314， 54 250， 57 736， 60 459， 63 029}

（2）原始数据序列的一次累加：

X={12 252， 26 387， 42 690， 61 417， 83 855， 110 362， 140 391， 172 059， 207 071， 245 042， 286 507， 332 289， 379 990， 429 739， 481 202， 532 516， 586 766， 644 502， 704 961， 767 990}

（3）对一次累加数列作的紧邻均值计算：

Z={19 319.5， 34 538.5， 52 053.5， 72 636， 97 108.5， 125 376.5， 156 225， 189 565， 226 056.5， 265 774.5， 309 398， 356 139.5， 404 864.5， 455 470.5， 506 859， 559 641， 615 634， 674 731.5， 736 475.5}

（4）B和Y已知，联立公式（5）、公式（6）求解a和u：

a=-0.064 984" " u=19 740.624 201

（5）得出模型方程式：

Xk+1=316 028.686 6e0.064 984k-303 776.686 6

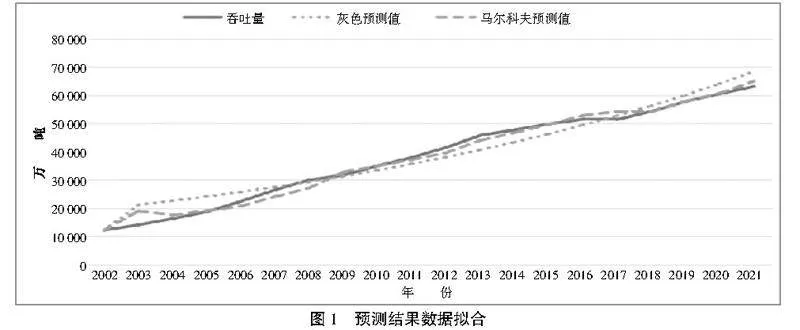
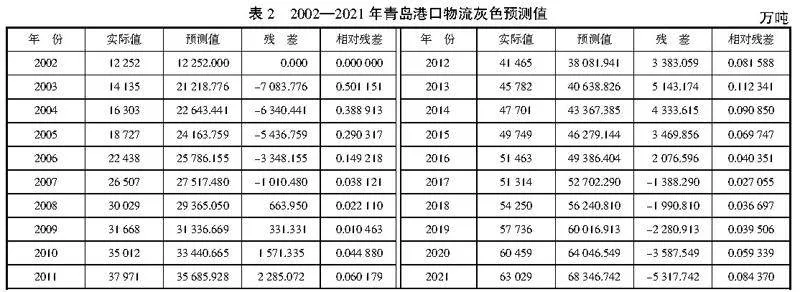
使用MATLAB软件计算出2002—2021年青岛港口灰色预测值、残差和相对残差（见表2）。预测2022—2026年港口物流吞吐量分别为72 935.656 6万吨、77 832.679万吨、83 058.495 7万吨、88 635.182 6万吨、94 586.297 5万吨。

3.3" 对预测结果进行马尔科夫修正

（1）划分状态区间

由表2数据可知，预测残差的区间范围在-7 100， 5 200区间内，将残差划分为5个状态，分别为-7 100， -4 640，-4 640， -2 180，-2 180， 280，280， 2 740，2 740， 5 200，进而得到2002—2021年对应状态区间分别为：

E， E， E， E， E， E， E， E， E， E， E， E， E， E， E， E， E， E， E， E

（2）以每年所在状态区间情况为基础，计算状态E一步转移到状态E的概率，建立如下状态转移矩阵：

P=

（3）修正预测值

" 计算5个状态区间的中间值分别为-5 870， -3 410， -950， 1 510， 3 970，以2003年的预测为例，2002年的数据处于状态3，由状态转移矩阵可知，2003年的数据处于状态1、状态2、状态3、状态4的概率均为1/4，2003年的灰色预测值为21 218.776万吨，进而可求出2003年的灰色马尔科夫预测值：

Z=21 218.776+×-5 870+×-3 410+×-950+×1 510=19 038.776（万吨）

" 同理，计算出其他年份的灰色马尔科夫预测值，如表3所示。

3.4" 预测精度检验

通过表2、表3可计算出，经过马尔科夫链修正过后绝对残差均值由原来的3 052.145 15变成了1 342.407 95，相对残差均值由0.107 359 751变成了0.049 700 424，灰色马尔科夫模型的误差要低于灰色模型，预测模型精度更高。下面对青岛港口吞吐量实际值与其两种模型预测值的拟合程度进行进一步分析。

通过对比图1中两种预测模型的结果，可以看到灰色模型的预测结果是一条较为光滑的递增曲线，与实际吞吐量相差较大。而灰色马尔科夫模型预测值的曲线波动性与实际吞吐量更为接近，反映出了吞吐量的波动情况，因此该模型能够较好地预测青岛港口2022—2026年的吞吐量。

3.5" 灰色马尔科夫模型预测2022—2026年港口货物吞吐量

" 由状态区间划分状况可知，2021年港口货物吞吐量处于状态E，初始转移向量P=2/3， 1/3， 0， 0， 0，表示的是2022年货物吞吐量残差在各区间的概率，所以2022年吞吐量的残差概率向量为：P=P=2/3， 1/3， 0， 0， 0。

根据公式（11）得2023—2026年港口货物吞吐量的残差概率向量分别为：P=P×P=0.555 6， 0.333 3， 0.111 1， 0， 0；

P=P×P2=0.509 2， 0.324 1， 0.138 9， 0.027 8， 0；P=P×P3=0.482 2， 0.312 5， 0.148 3， 0.051 4， 0.005 6；P=P×P4

=0.462 7， 0.302 0， 0.151 5， 0.069 3， 0.014 5 。

2022年吞吐量的马尔科夫灰色预测值=灰色预测值+马尔科夫修正值，即：

T=72 935.656 6+×-5 870+×-3 410=67 885.656 6（万吨）

同理利用2023—2026年残差发生的概率向量对灰色模型的预测结果进行修正，得到2022—2026年青岛市港口物流吞吐量预测值分别为67 885.656 6万吨、73 329.345 67万吨、78 874.051 26万吨、84 697.497 41万吨、90 858.231 14万吨。通过得到的预测值，可以看出青岛港口的物流需求总体上呈增长趋势。

4" 结论与建议

" 准确预测港口货物吞吐量，可以为港口发展战略的制订和港口配套设施的建设提供依据。本文使用马尔科夫优化的灰色预测模型对青岛市2002—2021年港口物流吞吐量进行了预测，并与传统GM1，1模型预测结果进行了比较。得出结论：马尔科夫灰色预测模型的平均残差和相对平均残差都低于GM1，1模型，预测精度更好；当原始数据具有波动性时，GM1，1模型预测精度较差，而采用马尔科夫理论修正的灰色模型预测结果也呈现出相似的波动性，与实际值更加接近，因此马尔科夫灰色预测具有更广泛的应用场景。

" 对青岛港口未来物流吞吐量的预测结果表明，青岛港口的物流需求正在迅速提升，为了保证青岛港口的稳定发展，对港口提出以下建议：

（1）提高信息化水准。青岛港口应进一步完善具有港口特色的信息平台。港口的信息平台主要服务于航行和交易信息的交流，每个客户都可以及时更新和接受物流信息，避免了信息交流不及时造成的失误。运用大数据、人工智能、第五代移动通信等技术可以提高信息平台的服务效率，为港口信息的使用者提供高质量的服务。

" （2）加强人才培养。在国内外“双循环”大趋势下，积极引进和培养高级物流技术人才，才能保证港口的稳步发展。政府可以鼓励企业与高校的联合，根据港口的需要开设相关性强的物流课程，培养与港口企业需求配套的高级物流人才。高校的物流相关课程也应与时俱进，多实践，多安排学生进行参观实习，方便学生认识港口物流的现状和需求，提前找准学习方向。科学的培养过程，能创造一批顺应时代发展的高级骨干精英，为港口的繁荣昌盛奠定基础。

" （3）优化港口发展方向。世界经济形势日新月异，青岛港口的发展重心也应有所调整。伴随着经济结构和消费区间的根本变化，政府应促进临港产业的发展，对临港产业链进行延伸，提高产业群的质量和效率，创造以航运、金融、产业于一体的新模式，推动港口产业升级，带动整个地区经济进步。

参考文献：

[1]" LI Y， LI T， ZUO Y， et al. A review of research on port throughput forecasting[C] // 2019 IEEE International Conference on Smart Internet of Things （SmartIoT）. IEEE， 2019：449-453.

[2] 陈治霖，胡鸿韬，边迎迎. 新冠疫情下基于SARIMA模型的上海港集装箱吞吐量预测[J]. 工业工程与管理，2024（1）：32-40.

[3]" FARHAN J， ONG G P. Forecasting seasonal container throughput at international ports using SARIMA models[J]. Maritime Economics amp; Logistics， 2018，20：131-148.

[4]" PATIL G R， SAHU P K. Estimation of freight demand at Mumbai Port using regression and time series models[J]. KSCE Journal of Civil Engineering， 2016，20：2022-2032.

[5]" GARGARI N S， PANAHI R， AKBARI H， et al. Long-term traffic forecast using neural network and seasonal autoregressive integrated moving average： Case of a container port[J]. Transportation Research Record， 2022（8）：236-252.

[6] 陈雄寅. 基于BP神经网络的港口物流需求预测研究[J]. 物流工程与管理，2022，44（12）：11-14，20.

[7] 孙晓聪，付玉慧. 基于RF-双向LSTM的集装箱吞吐量预测[J]. 上海海事大学学报，2022，43（1）：60-65.

[8] 蔡婉贞，黄翰. 基于BP-RBF神经网络的组合模型预测港口物流需求研究[J]. 郑州大学学报（工学版），2019，40（5）：85-91.

[9]" JIAO Y， LI L， ZHU Z， et al. Forecast of port freight volume based on grey RBF neural network combination model[C]// Sixth International Conference on Electromechanical Control Technology and Transportation （ICECTT 2021）. SPIE， 2022，12081：565-571.

[10] 赵龙文，苌道方，朱宗良，等. 基于SARIMA-BP模型的港口船舶交通流量预测[J]. 中国航海，2020，43（1）：50-55，94.

[11]" HUANG Y. Research on container throughput forecast of Qingdao Port based on combined forecasting model[C] // Proceedings of the 4th International Conference on Industrial and Business Engineering， 2018：99-103.

[12] 王向前，吴东隆，郑健彤. 货物吞吐量预测的改进ARIMAX方法——以天津港为例[J]. 运筹与管理，2022，31（3）：138-144.

[13] 邓萍，刘淑龙. 基于FGM-SVR组合模型的港口吞吐量预测[J]. 重庆交通大学学报（自然科学版），2023，42（8）：132-138.

收稿日期：2024-01-12

基金项目：武汉市2022年度知识创新专项基础研究项目（2022010801010301）

作者简介：刘心宇（1995—），男，湖北天门人，武汉科技大学管理学院硕士研究生，研究方向：物流与供应链管理；邓旭东（1964—），男，湖北云梦人，武汉科技大学管理学院，教授，硕士生导师，研究方向：管理优化与决策、物流与供应链管理。

引文格式：刘心宇，邓旭东. 基于灰色马尔科夫模型的青岛市港口物流需求预测[J]. 物流科技，2025，48（3）：16-20.