MPCVD装置冷却水温度的自抗扰控制策略

摘" 要： 针对MPCVD装置冷却水温度控制中存在的调节时间长、稳定性能差的弊端，提出一种将改进后的混沌蛇鹫优化算法（CSBOA）与自抗扰控制（ADRC）算法结合的控制策略。首先，给出了冷却水温度控制系统的结构及数学模型，设计自抗扰控制器；其次，通过混沌蛇鹫优化算法对自抗扰控制器的部分参数迭代寻优，解决人工调整参数的问题。对系统进行了仿真和实验验证，结果表明：相比于传统PID控制，该控制系统稳态时的温度误差更小，具有更好的温度控制效果，有效避免了冷却水温度波动对金刚石薄膜制备产生的不良影响。

关键词： MPCVD； 冷却水温度； 自抗扰控制； 蛇鹫优化算法； 参数整定； 金刚石薄膜制备

中图分类号： TN876⁃34； TP273" " " " " " " " " "文献标识码： A" " " " " " " " " " " 文章编号： 1004⁃373X（2025）03⁃0104⁃07

Active disturbance rejection control strategy for cooling water

temperature of MPCVD unit

ZHANG Hebin， REN Tianping， SU Yufeng

（School of Mechanical and Power Engineering， Zhengzhou University， Zhengzhou 450001， China）

Abstract： In view of the disadvantages of long adjustment time and poor stability of cooling water temperature control in MPCVD unit， a control strategy combining the improved chaotic secretary bird optimization algorithm （CSBOA） with the active disturbance rejection control （ADRC） algorithm is proposed. Firstly， the structure and mathematical model of the cooling water temperature control system are given， and the ADRC is designed. Secondly， the CSBOA is used to iteratively optimize some parameters of the ADRC to adjust the parameters manually. The simulation and experimental verification of the system show that in comparison with the traditional PID control， the temperature error of the proposed control system in steady state is smaller， and it has better temperature control effect， and can effectively avoid the adverse influence of the fluctuation of cooling water temperature on the preparation of diamond film.

Keywords： MPCVD; cooling water temperature; ADRC; SBOA; parameter setting; preparation of diamond film

0" 引" 言

MPCVD（微波等离子体化学气相沉积）装置是一种优异的金刚石薄膜培育设备[1]。它通过将气体化学物质注入反应室并在微波等离子体中激发，从而在衬底表面沉积出薄膜材料。研究表明，薄膜生长对温度的变化十分敏感，一旦MPCVD装置的基底出现短时高温将极大影响金刚石薄膜的质量[2]。实际操作中，通常采用水冷的方式对基底进行冷却，使晶种生长维持在一定的温度范围内。在长时间的沉积过程中，精准控制冷却水温度有利于制备高品质的金刚石薄膜。

文献[3]提出一种模糊自适应PID控制温度的方法，但模糊PID的待调节参数更多，且受系统的建模误差、外部扰动影响较大；文献[4]提出一种将改进鲸鱼算法与神经网络PID控制算法相结合的控制方法，但整体控制系统的复杂性增加，影响实时性和响应速度。

文献[5]提出了自抗扰控制（Active Disturbance Rejection Control， ADRC）策略，该控制通过预先估计和补偿系统的扰动，实现无超调、高精度的效果。ADRC控制器耦合参数过多，实际中往往由于参数整定不合理而影响控制精度。目前多采用智能优化算法（如遗传算法、粒子群算法等）对ADRC控制器的参数进行优化[6]，使系统性能达到最优。蛇鹫优化算法（Secretary Bird Optimization Algorithm， SBOA）是一种受自然启发的群智能优化算法，灵感来自于蛇鹫在自然环境中的生存行为[7]。SBOA在解决方案质量、收敛速度和稳定性方面有出色的性能，拟采用改进后的蛇鹫算法整定ADRC的参数。

针对MPCVD设备冷却水温控系统的优化需求，本文提出一种改进型蛇鹫优化算法的ADRC控制器，实现近乎无超调、高精度的控制效果，并设计相应的硬件电路，提高了温控系统的响应速度和稳定性。

1" 冷却水温控系统模型

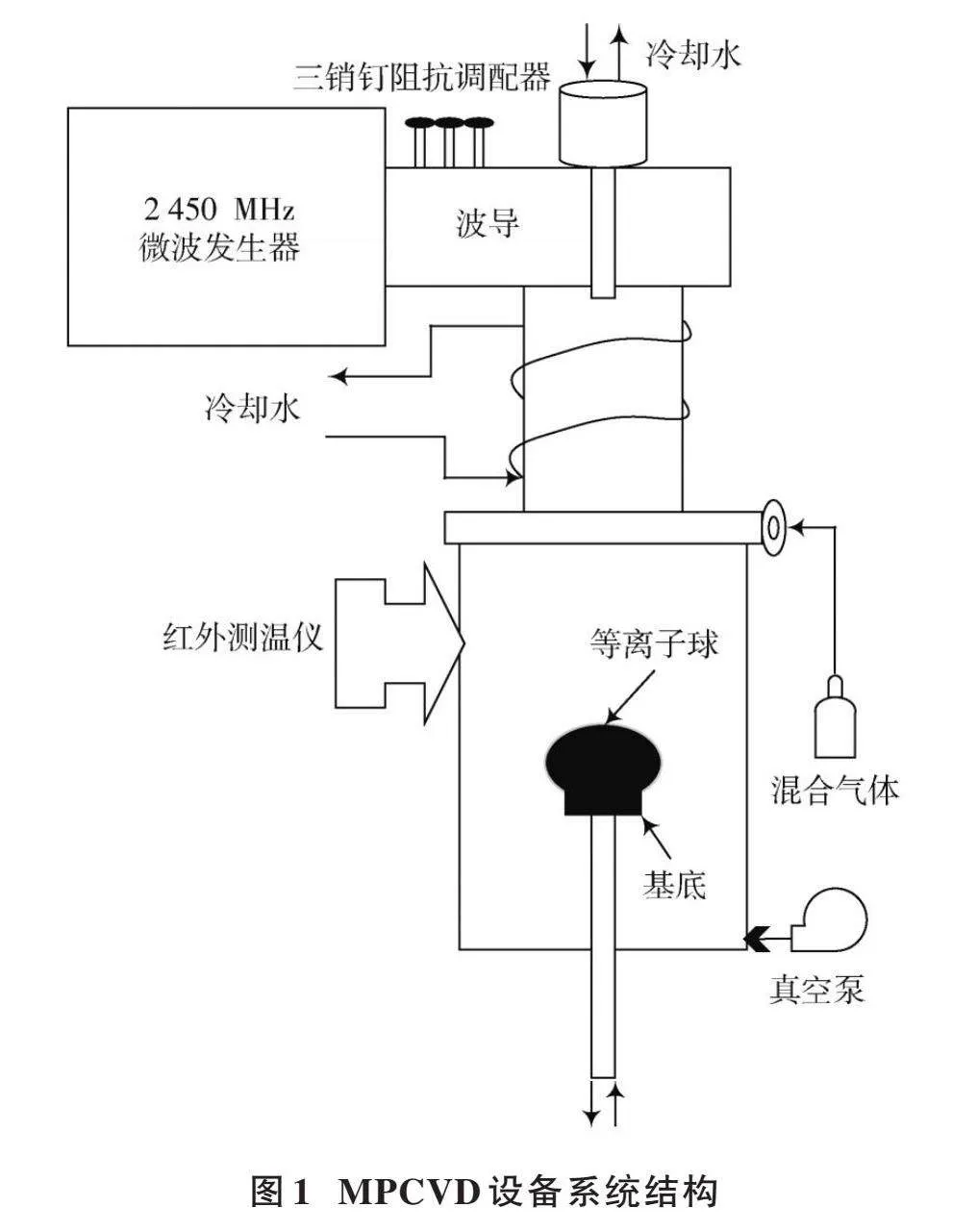
MPCVD设备采用循环水冷系统进行散热，如图1所示。冷却水通过管道流经MPCVD设备内部腔体，以热传导的方式将基底温度控制在一定范围内。

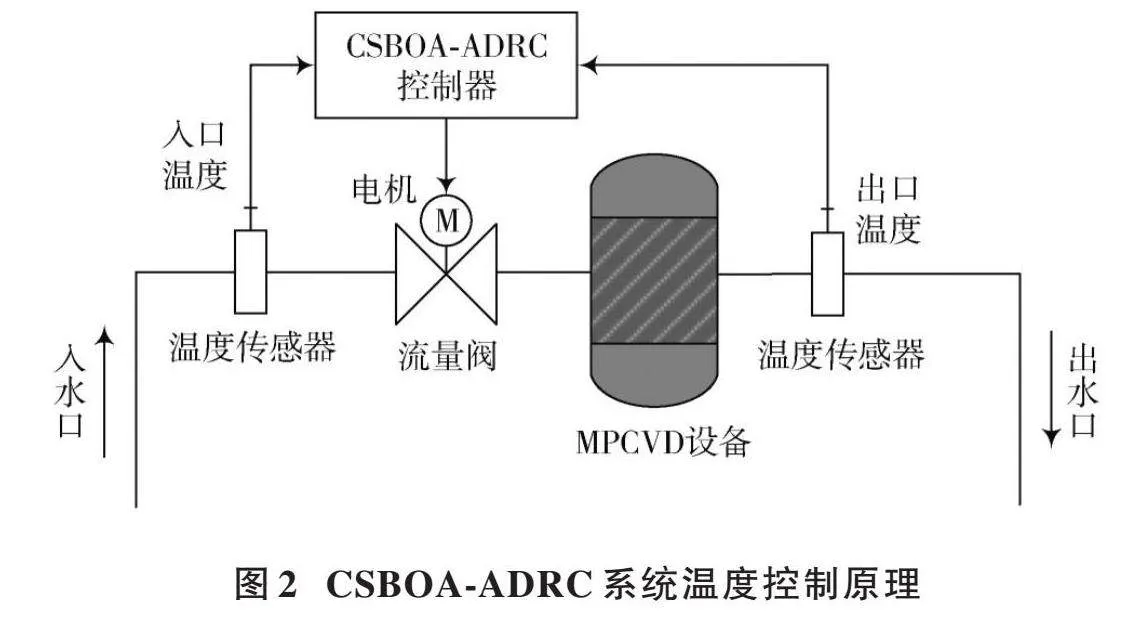
系统的温度控制原理如图2所示。温度传感器测量冷却水的温度，控制器根据设定水温与实际测得水温之间的偏差，利用CSBOA⁃ADRC控制算法得到步进电机的位移调整量，带动丝杠螺母上下移动，以改变流量调节阀的开度，对出口水温进行控制。

系统传递函数可表示为：

[G（s）=G1（s）G2（s）G3（s）G4（s）] （1）

式中：[G1（s）]为步进电机环节传递函数；[G2（s）]为丝杠传动传递函数；[G3（s）]为流量调节阀环节传递函数；[G4（s）]为冷却水管道传递函数。

系统以步进电机为动力原件驱动丝杠，电机接收控制脉冲信号转过一个步距角[θi]，转子实际转过的角度[7]为[θ0]。通过振荡理论知识可以明确步进电机的传递函数如式（2）所示：

[G1（s）=θ0（s）θi（s）] （2）

该步进电机运动方程如式（3）所示：

[Jd2（δθ）d2t+Bd（δθ）dt-D2rLi2A2θ0=D2rLi2A2θi] （3）

等式两边进行拉普拉斯变换得到：

[Js2+Bs+D2rLi2A2θ0（s）=D2rLi2A2θi（s）] （4）

式中：[θ]、[J]、[D2r]分别为步进电机转子的角位移、转动惯量、齿数；[B]为步进电机的粘滞阻尼系数；[L]为步进电机的自感；[iA]为步进电机的A相电流。

整理后得到步进电机环节的传递函数为：

[G1（s）=θ0（s）θi（s）=D2rLi2A 2Js2+BJs+D2rLi2A 2J] （5）

丝杠传动简化为比例环节，输入转角[θ0]，输出转角[θ']，传递函数如式（6）所示：

[G2（s）=θ'（s）θ0（s）] （6）

采用流量阀对冷却水的流量进行控制。流量阀在靠近全关或全开状态时，其流量[q]⁃开度[θ]特性曲线变得平缓，而在多数中间开度范围内趋近于线性关系[8]。基于此，流量阀调节环节简化为比例环节，表示为：

[G3（s）=q（s）θ（s）=Kf] （7）

根据耦合传热数值计算理论，冷却水管道中传热过程存在大滞后、大惯性等特点，采用的是一阶惯性纯滞后环节，传递函数为：

[G4（s）=Ke-τsTs+1] （8）

分析得出总传递函数为滞后的三阶系统，以循环冷却水的温度为控制变量，上位机采集冷却水温度阶跃响应数据，使用Matlab系统辨识工具箱进行参数辨识，获得系统传递函数如式（9）所示：

[G（s）=156.48s3+0.34s2+160.23s+0.48se-2.2s] （9）

2" 自抗扰控制器算法设计

冷却水的温度控制过程滞后且非线性，采用传统的PID控制效果不佳，而自抗扰控制将外部扰动进行估计并补偿[9]，实现对冷却水温度的精准控制。

2.1" ADRC控制器设计

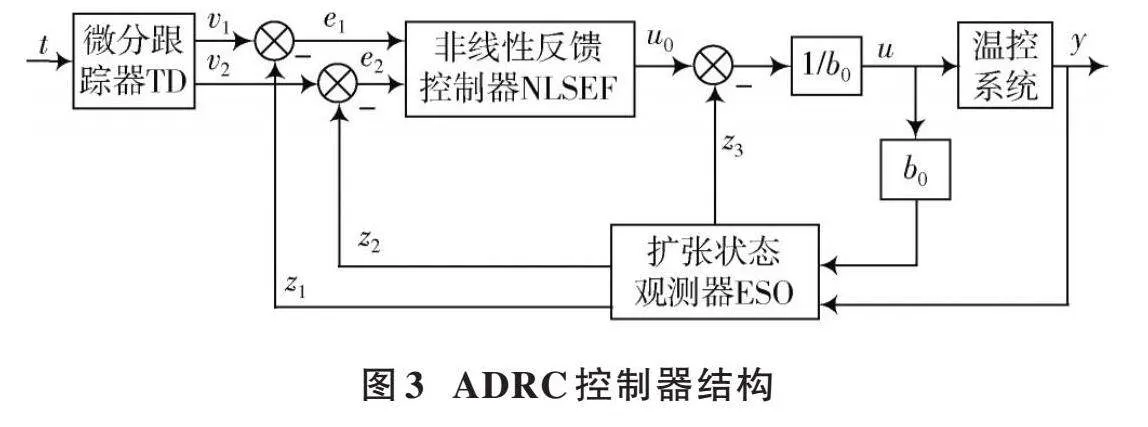
ADRC控制器由三部分构成：微分跟踪器TD、非线性状态误差反馈控制器NLSEF和扩张状态观测器ESO[10]。典型的ADRC控制器结构如图3所示。

TD预先对设定温度[t]安排过渡过程[t1]及其微分信号[t2]。ESO用冷却水的出口温度[y]和控制器的输出量[u]来估计系统的扰动与当前状态，得到[v1]的跟踪信号[z1]与[v2]的跟踪信号[z2]以及总扰动实时量[z3]。NLSEF通过计算输出[u0]，再用系统所受总扰动值[z3]对误差反馈进行补偿，获得最终输出的步进电机位移量[u]。为实现冷却水温控系统的干扰跟踪和温度补偿，下面对三个部分进行设计。

ADRC通过TD提前对设定温度的过渡过程和微分信号进行调节。其动态方程为：

[t1（k+1）=t1（k）+T⋅t2（k）t2（k+1）=t2（k）+T⋅fh" " fh=fhant1（k）-t，v2（k），r，h] （10）

式中：[t]为设定温度；[T]为温控系统采样周期，[T]=0.15 s；函数fhan（ ）为离散系统最速控制综合函数；[r]为速度因子；[h]为滤波因子。

扩张状态观测器ESO把[k]时刻冷却水温控系统计算的调整量[uk]和系统输出的温度[y（k）]作为输入，其动态方程为：

[ek=z1（k）-y（k）z1（k+1）=z1（k）+Tz2（k）-β01ekz2（k+1）=z2（k）+Tz3（k）-β02falek，0.4，λ+b0ukz3（k+1）=z3（k）-T⋅β03fal（ek，0.25，λ）] （11）

式中：[β01]、[β02]、[β03]为观测参数；[b0]为冷却水温控系统增益；fal（ ）是一种非线性函数，防止高频振荡。

fal（ ）的表达式为：

[ fal（e，α，δ）=eλ1-αs+eαsgn（e）（1-s）， s=sgn（e+λ）-sgn（e-λ）2] （12）

NLSEF是利用非线性状态反馈实现高效控制，解决了PID调节器的缺陷。具体是由TD产生的跟踪信号[v1]及其微分[v2]与ESO给出的状态估计[z1]、[z2]，分别形成了误差[e1]、[e2]作为NLSEF的输入信号，通过内部线性组合输出[u0]，结合控制扰动[z3]，除以冷却水温控系统的控制器增益[b0]，得到最终输出信号[u]，其动态方程为：

[e1（k）=t1（k）-z1（k）e2（k）=t2（k）-z2（k）u0=β1⋅fale1，0.75，λ0+β2⋅fale2，1.5，λ0u（k）=u0-z3（k）b0] （13）

式中：[β1]、[β2]分别为比例因子和微分因子。

2.2" ADRC参数整定

TD有[h]、[r]两个参数，其中[r]越大，快速性越好，但容易导致超调和振荡；[h]越大，静态误差越小，但会导致上升过慢，快速性不好。根据文献[11]，通常可以取[r]=30，[h]=0.01。

ESO参数[β01]、[β02]、[β03]、[b0]决定了冷却水温控系统的动态特性。[β01]、[β02]、[β03]越小，系统的响应速度越快。[β03]越大，跟踪速度越快，但系统输出的振荡变大。[b0]在冷却水温控系统模型不精确时作为调整参数[12]。

NLSEF的[β1]、[β2]与PID中的比例系数和微分系数相似。[β1]适当增大可减小系统的超调现象，但会降低快速性；[β2]增大会增加快速性，但过大会引起振荡。

综上所述，ADRC控制器最终需要最优化整定的参数有[β01， β02， β03， b0， β1， β2]。针对ADRC的参数难整定以至于影响控制精度的问题，蛇鹫算法因其在解决复杂、非线性优化问题中的显著优势而逐渐受到研究人员的青睐[13]。

3" CSBOA⁃ADRC控制算法设计

3.1" 基本SBOA算法

蛇鹫优化算法利用蛇鹫的生存能力，以解决现实世界的优化问题[13]。该算法在种群初始化后，先后进入探索阶段和开发阶段。探索阶段模拟蛇鹫捕猎，开发阶段模拟蛇鹫逃离捕食者，这两个阶段不断迭代，以找到优化问题的最优解。

3.1.1" 种群初始化

在SBOA中，优化从候选解的种群开始，蛇鹫集合矩阵如式（14）所示：

[X=x11x12…x1dx21x22…x2d⋮⋮⋱⋮xn1xn2…xnd] （14）

式中：[d]为蛇鹫种群维度；[n]为种群数量。

SBOA种群的适应度矩阵表示如下：

[Fx=f[x11x12…x1d]f[x21x22…x2d]⋮⋮⋱⋮f[xn1xn2…xnd]] （15）

式中[f]为蛇鹫个体的适应度值。

个体在搜索空间中的位置决定了决策变量的值，式（16）用于随机初始化搜索空间中蛇鹫的位置。

[Xi，j=Lbj+r⋅Ubj-Lbj] （16）

式中：[Xi，j]为第[i]只蛇鹫在第[j]维的位置；[Lbj]和[Ubj]分别是给定问题的下限和上限。

3.1.2" 捕猎阶段

蛇鹫以蛇为食时的捕猎行为有三个阶段：寻找猎物、消耗猎物和攻击猎物。

蛇鹫从寻找潜在的猎物开始，位置更新如下：

[Xi=Xnew，P1i，" " Fnew，P1ilt;FiXi，" " 其他 ] （17）

[xnew，P1i，j=xi，j+xr1-xr2⋅R1] （18）

式中：[Xi]为第[i]个蛇鹫个体；[Xnew，P1i]为第[i]只蛇鹫的新位置；[xr1]和[xr2]是第一阶段迭代的随机候选解；[R1]为（0，1）中随机生成1×[d]的数组；[xnew，P1i，j]表示捕猎阶段第[j]维的值；[Fnew，P1i]表示目标函数的适应度值。

蛇鹫发现猎物后不直接战斗，而是逐渐激怒它，从而消耗对手的耐力。在此阶段，引入布朗运动（[Rb]）来模拟蛇鹫的随机运动。消耗猎物的位置更新如下：

[Rb=randn（1，d）] （19）

[xnew，P1i，j=xbest+expt4T4⋅（Rb-0.5）⋅xbest-xi，j] （20）

式中：[xbest]表示当前最优适应度值；[randn（1，d）]表示从标准正态分布中生成的1×[d]的数组。

当猎物无力挣脱时，蛇鹫迅速发动攻击，位置更新如下：

[xnew，P1i，j=xbest+1-t T2t T⋅xi，j⋅R1] （21）

式中[1-t T2t T]为引入的非线性扰动因子。

3.1.3" 逃生阶段

当出现大型食肉动物后，蛇鹫有两种方式保护自身：逃跑或伪装，两种情况等概率发生。

[xnew，P2i，j=C1：xbest+（2Rb-1）⋅xi，j，" " "randlt;12C2：xi，j+R2⋅xr-K⋅xi，j，" " "其他] （22）

[Xi=Xnew，P2i，" " " Fnew，P2ilt;FiXi，" " " 其他] （23）

式中：C1对应环境伪装；C2对应逃跑；[Xnew，P2i]表示逃生阶段第[i]维的值；[R2]表示随机生成维度为1×[d]的数组；[xr]表示当前迭代的随机候选解；[K]表示整数为1或2的随机选择。[K]可由式（24）计算：

[K=round1+rand（0，1）] （24）

式中[rand（0，1）]表示在（0，1）之间的均匀随机数。

3.2" CSBOA算法

基本蛇鹫算法由于概率都是（0，1）间的随机数，寻优过程有较大随机性，易使算法困于局部最优[14]。混沌运动在求解函数优化问题时能够使算法逃离局部最优解，从而维持种群的多样性。为弥补蛇鹫优化算法种群初始化不均，引入混沌序列生成具有混沌初始化种群的混沌蛇鹫优化算法（CSBOA）。

生成初始化种群位置时可使用的混沌映射有多种，其中Tent混沌映射的遍历均匀性好，能在（0，1）之间产生分布较均匀的初始值。首先通过映射产生混沌序列，再将其转化至个体的搜索空间[15]。改进后的Tent映射如式（25）所示：

[xn+1=2xn+1Zrand（0，1），" " "0≤x≤1221-xn+1Zrand（0，1），" " " 12lt;x≤1] （25）

式中：[xn]为第[n]个混沌数；[Z]为混沌序列的粒子数。

在Matlab环境初始化一个全0的混沌序列，然后通过迭代公式生成Tent映射混沌序列，由图4可知，改进后的混沌序列更加均匀，能提升初始种群的多样性及种群解的数量，提高算法的求解效率。

3.3" 算法验证

为了验证改进的蛇鹫算法，拟对CSBOA的寻优精度与快速性进行测试。测试参数设置如下：蛇鹫种群数量[n]=30，测试维数[d]=100，放弃阈值limit=100。

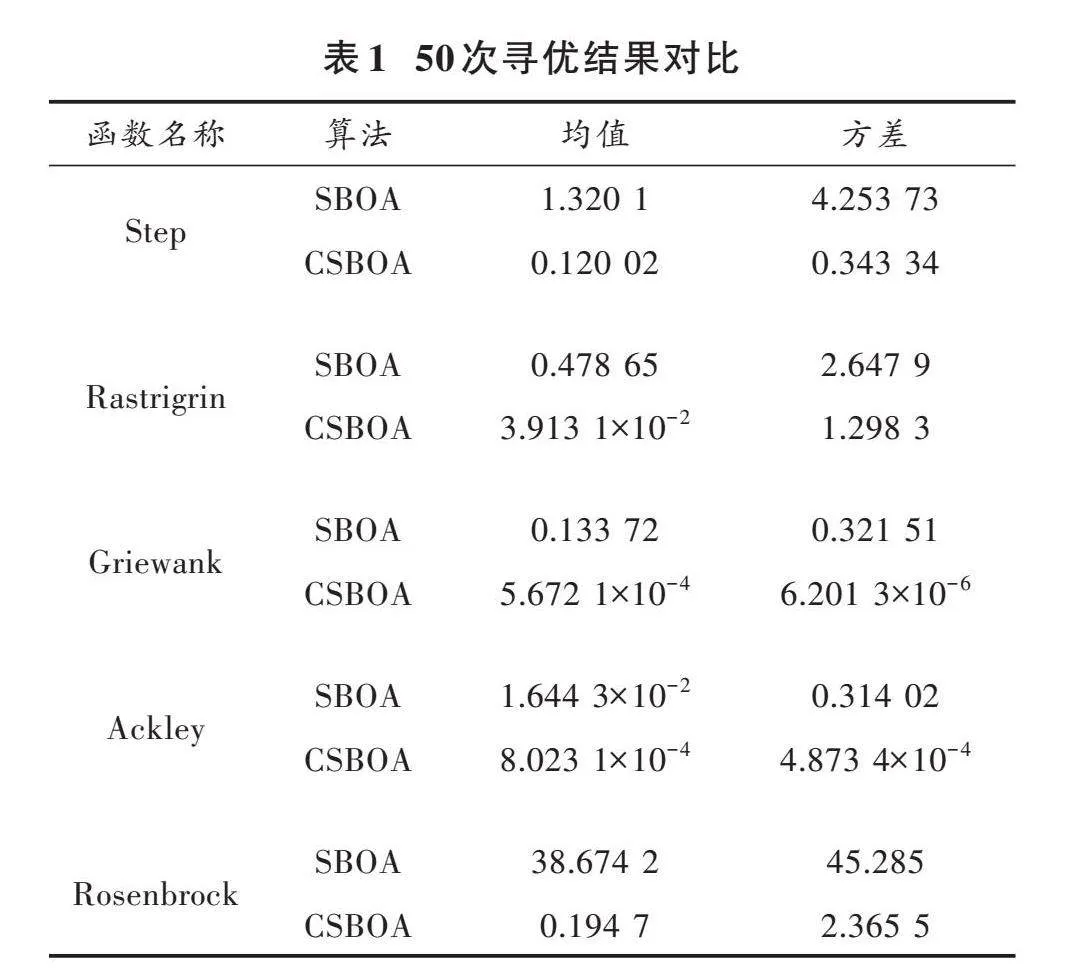
采用5个复杂函数测试，选取50次测试结果中的均值和方差2个指标来代表算法的寻优精度[16]，其结果如表1所示。

从表1的50次寻优结果可以看出，在同一测试函数下，相较于传统SBOA算法，CSBOA算法得出的解的质量明显优于前者，寻优精度更好，算法稳定性也更高，能够更快找到最优解。

选取ITAE指标作为算法的目标函数，其数学表达式如下：

[F=0Tte（t）dt] （26）

分别采用两种算法对ADRC参数在线优化，其适应度随迭代次数变化如图5所示。

从图5可以看出，传统SBOA算法极易收敛到局部最优解，而引入Tent序列混沌映射后，CSBOA算法迭代至163次后稳定收敛到全局最优值，在保持极高的寻优精度下，具有更快的收敛速度，验证了CSBOA具有较强的跳出局部最优解的能力。

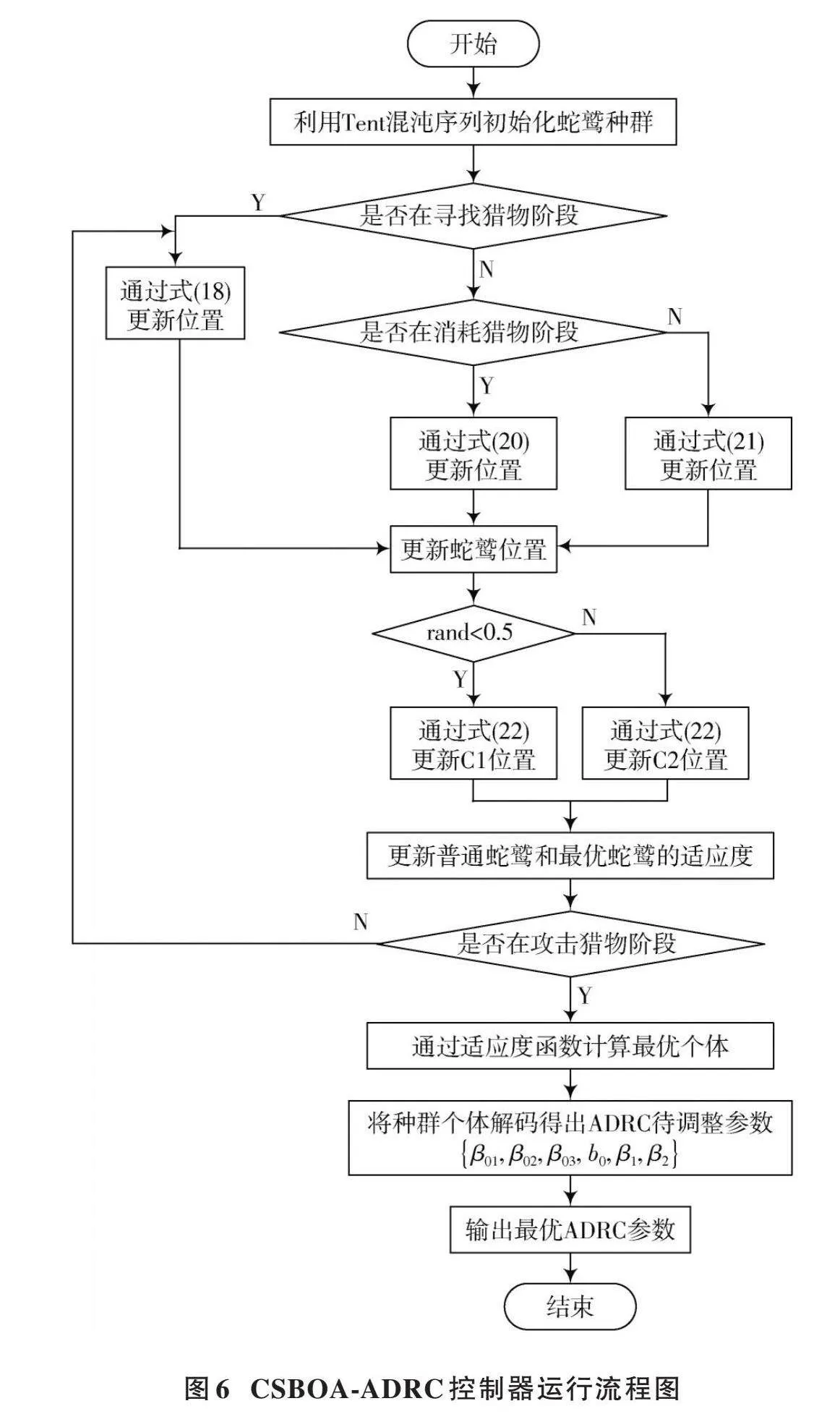
在人工整定的基础上确定各参数的近似范围后，将改进后的混沌蛇鹫优化算法与ADRC控制器结合，对ADRC的参数进行实时优化更新，CSBOA⁃ADRC控制器运行流程图如图6所示。

4" 系统仿真与实验验证

4.1" 温度控制系统仿真

在Matlab/Simulink平台上对冷却水温度控制系统进行仿真实验。设定采样周期为0.15 s，PID参数[Kp]、[Ki]、[Kd]分别为0.874、3.544、0.107。ADRC参数为：[b0]=22；[β1]和[β2]分别为12、4；[β01]、[β02]、[β03]分别为34、127、200。对于CSBOA⁃ADRC控制器，其待整定参数为[β01， β02， β03， b0， β1， β2]，可实时优化调整，设定其最小值为{0，0，0，0，0，0}，最大值为{50，200，1 000，50，50，10}。同时，在CSBOA控制器中设置种群规模30，最大迭代次数为500。

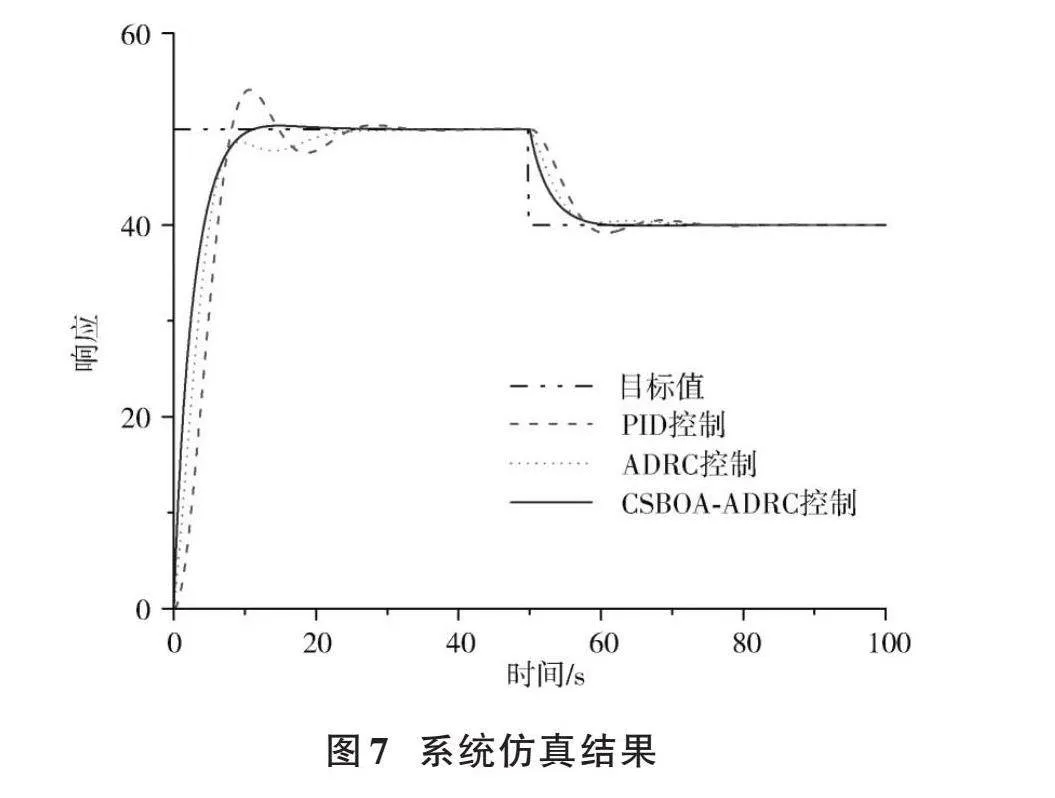
在阶跃信号的激励下，分别采用人工整定PID控制、人工整定ADRC控制、CSBOA⁃ADRC控制这三种控制策略，得到系统仿真响应曲线如图7所示。

通过仿真结果看出：系统达到目标温度需要的调节时间分别为26.5 s、23.6 s、11.4 s；超调量分别为9.6%、4.2%、1.2%。比较后得出：人工整定PID参数的方式超调量过大；采用人工整定ADRC虽无明显超调，但响应速度过慢；而采用CSBOA⁃ADRC控制时，经过迭代寻优后获得的参数能有效提升控制精度，且系统几乎无超调量，调节速度更快。

4.2" 系统实验分析

某企业的MPCVD设备冷却水温度控制系统冷却水装置如图8所示。

分别采用PID算法和CSBOA⁃ADRC算法对冷却水温度进行控制。

为了验证冷却水温度控制系统的控制效果，上位机设定冷却水温度为44℃，对系统分别采用两种控制算法进行了对比实验。温度控制效果和误差对比如图9、图10所示。

从图9和图10可以看出，与人工调参的PID算法相比，CSBOA⁃ADRC算法的控制精度更好，几乎无超调与振荡，温度误差范围最大为[±0.2 ℃]。

5" 结" 论

MPCVD设备冷却水的温度对合成超硬材料的质量有不可忽视的影响，针对以往PID控制冷却水温度时存在调节速度慢、温度稳定性能差、易受干扰影响等问题，本文设计了基于CSBOA⁃ADRC算法的冷却水温控系统。通过仿真与实验结果表明，与传统PID控制相比，系统采用CSBOA⁃ADRC控制策略可显著提升控制精度，减小超调量，有效改善冷却水温度控制效果，能够确保MPCVD设备在适宜的工作温度范围内稳定运行，同时对其他具有大惯性、大迟滞的控制系统提供了一种可靠的解决方案。

注：本文通讯作者为张贺斌。

参考文献

[1] 马孟宇，蔚翠，何泽召，等.氢终端金刚石薄膜生长及其表面结构[J].物理学报，2024，73（8）：312⁃317.

[2] 金帅.微波化学气相沉积腔内等离子体特性及反应过程数值模拟[D].哈尔滨：哈尔滨工业大学，2020.

[3] 赵亮，陈惠贤，姚运萍.基于Smith⁃模糊PID的风干区温度控制系统设计[J/OL].控制工程：1⁃8[2023⁃11⁃28].https：//doi.org/10.14107/j.cnki.kzgc.20221108.

[4] 黄祥辉，朱晓东，任天平，等.金刚石压机冷却水温控系统的设计[J].机床与液压，2024，52（4）：93⁃99.

[5] 韩京清.自抗扰控制技术[J].前沿科学，2007（1）：24⁃31.

[6] 刘欣，罗晓曙.附加惯性项神经网络云台自抗扰控制研究[J].现代电子技术，2020，43（3）：154⁃157.

[7] FU Y F， LIU D， CHEN J D， et al. Secretary bird optimization algorithm： A new metaheuristic for solving global optimization problems [J]. Artificial intelligence review， 2024， 57（5）： 123.

[8] 彭宇浩.砂芯烘干线控制系统的设计[D].郑州：郑州大学，2022.

[9] 方俊峰，李醒飞，李洪宇，等.水下多次级供电系统稳压策略研究[J].海洋湖沼通报，2023，45（6）：51⁃59.

[10] 刘晓伟.电动汽车动态无线充电温度与磁场检测技术的研究[D].哈尔滨：哈尔滨工业大学，2019.

[11] 谭龙彪，肖金凤.基于改进麻雀算法的卷绕张力控制系统[J].轻工机械，2022，40（2）：67⁃73.

[12] 文定都.ADRC串级控制在电加热炉温度控制中的应用研究[J].仪表技术与传感器，2015（6）：59⁃62.

[13] 刘勇，杨浩，马士翔，等.基于并网逆变器的级联线性自抗扰控制策略[J].控制工程，2023，30（5）：788⁃795.

[14] 付博妍，毕千惠，郑诗雨，等.基于多维光场调控的超构表面先进成像与显示研究[J/OL].光学学报：1⁃41[2024⁃03⁃18].http：//kns.cnki.net/kcms/detail/31.1252.O4.20240314.1221.084.html.

[15] 张泽鹏，茅云生，傅何琪，等.基于混沌麻雀算法的船用焊接机器人轨迹优化[J].船舶工程，2022，44（5）：134⁃140.

[16] 吕丽霞，罗磊，王鹏飞，等.改进人工蜂群算法及在自抗扰控制上的应用[J].热能动力工程，2017，32（4）：80⁃85.