基于模糊集的无线通信网络码间干扰时序抑制算法

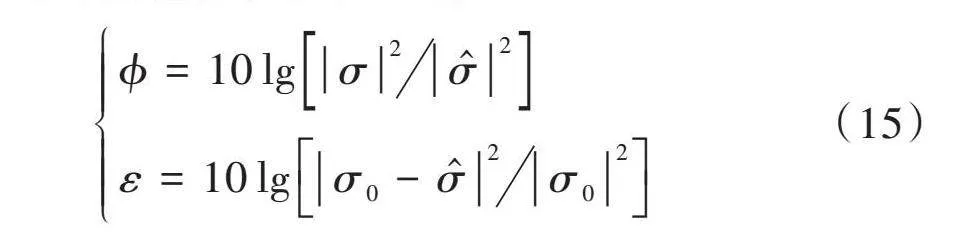
摘" 要： 受到码间干扰影响，无线通信网络的通信传输过程不够稳定且存在一定风险，而信道状态的不确定性和时变性，增加了干扰抑制的实时性，由此，提出基于模糊集的无线通信网络码间干扰时序抑制算法。建立无线通信网络通信信道模型并展开信道多径特性测量，以分析无线通信网络中信道的行为特性；基于该特性，采用基于贝叶斯滤波的信道估计方法实时跟踪并准确估计信道状态，为码间干扰抑制提供基础；将估计结果作为输入，选用基于模糊神经网络的盲均衡算法，通过模糊集理论和盲均衡器实现码间干扰时序抑制，增强无线通信网络性能。实验结果表明，所提方法可以有效降低码间干扰的影响，为无线通信网络的稳定传输提供有力的保障。

关键词： 信道模型； 多径特性测量； 贝叶斯滤波； 信道估计； 模糊神经网络； 盲均衡器； 模糊集； 码间干扰抑制

中图分类号： TN911⁃34" " " " " " " " " " " " "文献标识码： A" " " " " " " " " " " " " 文章编号： 1004⁃373X（2025）03⁃0013⁃06

A fuzzy set based algorithm for temporal suppression of inter symbol interference in wireless communication networks

TENG Yutong

（China Airborne Missile Academy， Luoyang 417009， China）

Abstract： Due to the influence of inter symbol interference， the communication transmission process of wireless communication networks is not stable enough and there are a certain risks. The uncertainty and time⁃varying of channel state requires higher real⁃time property of interference suppression. Therefore， a fuzzy set based algorithm for temporal suppression of inter symbol interference in wireless communication networks is proposed. A wireless communication network communication channel model is established and channel multipath characteristic measurements are conducted， so as to analyze the behavioral characteristics of channels in the wireless communication networks. On the basis of this characteristic， a channel estimation method based on Bayesian filtering is adopted to track and accurately estimate the channel state in real time， providing a foundation for inter symbol interference suppression. The estimation results are taken as the input. A blind equalization algorithm based on fuzzy neural networks is adopted to realize temporal suppression of inter symbol interference by the fuzzy set theory and blind equalizers， enhancing the performance of wireless communication networks. The experimental results show that the proposed method can reduce the impact of inter symbol interference effectively and provide strong guarantees for the stable transmission of wireless communication networks.

Keywords： channel model; measurement of multipath characteristics; Bayesian filtering; channel estimation; fuzzy neural network; blind equalizer; fuzzy set; inter symbol interference suppression

0" 引" 言

码间干扰是由多径传播和信道可变性等因素引起的，导致符号前后的相互干扰。它不仅降低了信号的传输质量，还可能导致误码率的严重增加和通信性能的下降[1]。

文献[2]提出结合高阶调制格式与时序控制技术的码间干扰时序抑制方案QPS dual⁃PCTW。通过Optisystem和Matlab联合模拟，建立16QAM和64QAM下的无线通信网络模型，根据该模型利用QPS dual⁃PCTW展开码间干扰的时序抑制，并对比有无该抑制方案的性能。方法结合了高阶调制格式与时序控制技术，增加了计算复杂性和实现难度。

文献[3]采用双向并行的结构，前向处理用于分析原始无线通信网络信道信号，反向处理则分析信号的时序反转形式。两方向均通过预处理技术和后处理策略（码间干扰抵消和均衡）展开优化。最终合并两个方向的处理结果，以获取准确的信道数据。由于需要同时处理正向和反向信号，并不利于实时性要求较高的通信系统。

文献[4]通过检测并定位无线通信网络码间干扰源，构建时序域变换矩阵设计码间干扰抑制策略，将干扰能量集中于信号中的特定点；通过置零操作去除这些干扰点，并采用预估计模块快速定位干扰中心，进而实现干扰抑制。该方法针对于干扰源的检测和定位不够稳定准确，对干扰抑制结果会产生一定影响。

文献[5]提出基于最大相关熵准则（MCC）的改进算法，该方法利用无线通信网络信号的恒模特性，计算发送信号与接收信号模值的码间时序误差，通过最大化误差参量的相关熵，获得迭代误差调节项，以实现码间干扰时序抑制。该方法的迭代收敛性会受到无线通信网络信道特性的影响，导致无法快速收敛。

以往的研究成果，虽然在一定程度上能够减轻干扰的影响，但在面对信道状态的不确定性和时变性时，其抑制效果往往受限。为了更有效地应对码间干扰问题，需要探索更有效的码间干扰时序抑制处理方法。对此，提出了基于模糊集的无线通信网络码间干扰时序抑制算法。

1" 信道模型建立及多径特性测量

无线通信网络通信信道是一个复杂且多变的系统[6]，其特性对信号的传输质量和码间干扰具有重要影响。为了理解并模拟这些信道特性，需要考虑复杂多径结构、传输频率和空间增益等因素，建立相应的信道模型，并进行多径特性测量，表示为冲激响应的形式，直观地展示信号在信道中的传播和变化。

1.1" 信道模型建立

无线通信网络信道受传输频率以及空间增益的影响，具有复杂多径结构，存在扩展和衰减损失[7]。在设计码间干扰时序抑制前，需理解并模拟这些信道特性，建立相应的信道模型。

给定平均传播损失[TL=m⋅10lgr+αr]，[m]和[r]分别表示传播因子、传播衰减，给定第[m]条路径的衰减损失[τmt]和冲击响应特性[smt]，建立无线通信网络信道模型：

[vτ，t=msmte-j2πgvτm（t）δt-τmt] （1）

式中[gv]表示信道码间干扰频率。

由式（1）推出无线通信网络信道脉冲响应为：

[ht=i=1psipt-τivτ，t] （2）

式中：[si]和[τi]表示不同路径的时间、频率分辨率。经正交幅度调制（QAM）[8]将无线通信信号分解为正、负信号，即[xk=x+k+x-k]，分别为[x+k=xk，" "xk≥00，" "xklt;0]和[x-k=xk，" "xklt;00，" "xk≥0]，以便后续分析。

1.2" 信道多径特性测量

信道多径特性测量是理解信道行为的关键步骤，主要通过测量不同路径的传播时间、传播损失等参量实现。假设无线通信网络信道多径特征参量为[V0VM2=0，VM-m=V∗m，m=0，1，2，…，M2-1]，其中[M]表示信号序列长度，[m]表示序列元素个数。

为了补偿多径效应带来的信号畸变，采用自适应均衡滤波器展开信道的调制解调，将分解后的无线通信信号通过IFFT（快速傅里叶逆变换）[9]得到多径特性下的信号。

[xk=m=0M-1Vm⋅ej2πkmM，" "k=0，1，2，…，M-1]" "（3）

式中[k]表示索引变量。

由于信号在传输过程中易受到波特率采样混叠效应导致的码间干扰，为估计不同路径的传播时间，需对经过多径信道与噪声干扰的扩频解调信号实施峰值检测，若满足条件[RVVυ1，υ2， β=RVυ1，tVυ2，t+β]，则可以估计出不同路径的传播时间。其中：[VV]表示处理后的信号；[υ1]、[υ2]表示不同路径时延；[β]表示码元速率。

假定无线通信网络通信信号为线性调频信号（LFM），通过拷贝相关得到自相关函数，以了解信号在不同时间点的相似性和相关性。

[Rt=WTWTsinπWT1-υ Tcos2πf0υ]" （4）

式中：[f0]表示信号中心频率；[WT]表示处理增益。由式（5）获取对应路径的传播时间和传播损失。

[f0RVVυ1，υ2，β=RtRVVυ1， βευ，t+βRVVυ1， β=RtEV∗υ， βVυ，t+β] （5）

这些测量值不仅有助于更准确地理解信道的特性，还为后续的信道估计和码间干扰抑制提供了重要依据。

2" 无线通信网络码间干扰时序抑制

2.1" 信道估计

在多径特性测量结果的初始化状态空间中，信道估计是无线通信中的关键，需要利用多径特性测量结果初始化相关参数，并引入状态空间模型，预测和更新连续跟踪信道状态，而贝叶斯滤波方法可以利用先验信息和观测数据实时更新信道状态，以提高码间干扰抑制实时性，以此进行信道估计。

1） 状态空间模型建立

为了描述信道状态随时间的变化，给定信道冲击响应基系数[bi]以及时域相关系数[Ei]，并通过提取[Ei]对角线元素向量[ei=vecEi]的方式建立模型，数学公式为：

[ei+1=ei+wibi+1=Eibi+htRtziyi=Sibi+li] （6）

式中：[Si]表示观测矩阵，通过2.1节中提到的不同路径的时间、频率分辨率统一描述；[wi]表示[ei]的过程噪声；[li]表示信道的加性复高斯白噪声；[yi]表示状态转移函数，通过传播损失[RVVυ1， β]调整，以反映信道中多径传播的影响。

在状态转移过程中，添加过程噪声向量[ui]和新状态变量[xi=eibiT]，将式（6）的状态空间模型转换为：

[xi+1=Tixi+uiyi=IQL012Ci12Ei]" "（7）

式中：[IQL]表示复数的实部和虚部[10]；[Ci=diagci]表示[i]时刻基系数的后验估计值[Ei]对应的对角矩阵。

2） 状态预测

在状态预测阶段，基于前一时刻状态变量的后验估计（信道冲激响应的基系数和时域相关系数等），根据式（7）推测下一时刻状态变量的先验估计值和不确定性[Pii-1]。

[xii-1=Ti-1xi-1Pii-1=Ti-1Pi-1TTi-1+Qu]" " （8）

式中[TTi-1]表示[i]时刻状态变量的先验协方差矩阵。

3） 状态更新

当新的观测数据（即接收到的无线通信网络通信信号）可用时，进入状态更新阶段。在这个阶段，使用观测数据以及观测方程来更新状态变量的估计值。观测方程描述了如何从接收到的信号中提取关于信道状态的信息，状态更新方程可表示为：

[Li=Pii-10AHi0AiPii-10AiT+Qz-1xi=xii-1+Liyi-0Aixii-1Pi=Pii-1-Li0AiPii-1] （9）

式中：[Li]表示贝叶斯滤波器增益[11⁃12]；[Qz]表示协方差矩阵。

利用卡尔曼增益计算贝叶斯滤波器增益，将观测数据与先验估计值结合，以获得更精确的后验估计[xi]。通过迭代贝叶斯滤波器的状态预测和状态更新步骤，连续追踪和更新信道状态，以便后续计算能够实时抑制突发的码间干扰。

2.2" 码间干扰时序抑制方法

无线通信网络中的码间干扰是由于信道的多径效应和时变性等因素引起的。基于模糊神经网络的盲均衡算法通过引入模糊集理论来处理信道特性的不确定性，通过模糊神经网络学习并适应信道状态，以便设计合适的均衡器来抑制码间干扰。整体算法步骤如下。

1） 信号接收

接收无线通信网络中受到码间干扰的信号，信号中含有信道叠加噪声[xi]，即：[yn=xi∗hn+nn]，其中，[hn]表示盲均衡器的期望输出，在此基础上将[yn]作为输入展开后续计算。

2） 模糊神经网络处理

第一层：输入层。包含[m+1]个神经元，负责接收来自信道估计的输出，并将其作为模糊神经网络盲均衡器的输入传递给下一层。

第二层：隶属函数层。包含[m+1]组神经元，各组神经元均与输入层相连，且输入层的第[j]个神经元与第[i]组的第[j]个单元直接连接。

使用高斯隶属函数[13]描述输入信号与模糊集合之间的关系，反映信道对信号的时序影响。其中的隶属度函数（高斯隶属函数）初值为2.1节中的信道估计结果，且信道估计参数的平均值作为中心，方差作为宽度。

由此生成隶属度值：

[o2ji=yn-1，" O2ji=go2ji，" i=1，2，…，k]" （10）

第三层：规则层。包含[k]个神经元，其中第[j]个神经元负责接收隶属函数层第[j]组的输入。基于隶属度值和预设的模糊规则展开推理（模糊规则由模糊集合表示输入和输出的可能范围或状态），得到该层的输出作为均衡器所需的调整信息。

[o3ji=gyn-i，" "O3ji=i=0mgyn-i]" （11）

第四层：输出层。根据规则层的输出，调整均衡器的参数，生成抑制码间干扰后的输出信号[kn]。

[o4ji=i=0mxigyn-ikn=O4ji=i=1kwji=0mxigyn-ii=1ki=0mgyn-i]" （12）

式中[wj]表示输出层权值。

3） 代价函数计算

根据均衡器的输出[kn]和期望的输出信号[hn]计算代价函数，作为评估函数[14]。

[J=12kn2-R2R2=Ekn4Ekn2]" " " （13）

式中[R2]表示决定系数。

4） 最小均方（LMS）算法迭代

利用LMS算法[15]和最速下降法，根据代价函数的梯度信息更新模糊神经网络的权值和参数，以最小化代价函数。

[wjn+1=wjnR2-ηw∂J∂wjnmjin+1=mjinR2-ηm∂J∂mjiσjin+1=σjinR2-ηδ∂J∂σji]" " " （14）

式中：[wjn+1]、[mjin+1]分别表示无线通信网络权值、高斯隶属函数中心宽度；[η]表示学习步长。

5） 迭代优化

持续迭代上述步骤，当代价函数的最终值小于预设阈值后，停止迭代。

6） 判决与输出

经过模糊神经网络盲均衡器处理后，得到的输出信号[kn]接近于原始发送信号，码间干扰得到了抑制。

将均衡器的输出[kn]送入判决器展开判决，得到最终的判决信号[kn]作为经时序抑制码间干扰后的无线通信网络通信真实信号。

3" 实验与分析

选取某一占地约75.8万m2的大学园作为实验场地，其无线通信系统的载波频率为2.4 GHz，且完全覆盖大学园内的所有区域。由于大学园内环境复杂，多径效应和信道动态性明显，因此模拟多径信道环境，并设定不同的时延扩展、多普勒频移等参数，如表1所示，以全面测试算法在不同信道条件下的性能。

在模拟信道环境中发射无线信号，在接收端捕获并接收这些信号。过程中信噪比设定范围为5～30 dB以覆盖从较差到较好的信号质量范围，所提方法采用的贝叶斯滤波信道估计算法的初始参数设定如下。

1） 滤波器学习率为0.01，以确保算法能够在稳定性和响应速度之间取得平衡。

2） 调制方式为QAM，调制阶数为4阶。

3） 滤波器超参数设置为0.01以防止过拟合；遗忘因子根据信道变化的快慢设定，通常为0.9～1之间。

表1" 多径信道参数

[信道条件 信道特性 多径时延参数/ms C1 延时差=网络带宽宽度 （0，1.3，2.4，，3.6，4.8） C2 延时差gt;网络带宽宽度 （1，1.3，2.4，3.6，6.2） C3 延时差lt;网络带宽宽度 （0.4，0.6，0.7，0.8，0.9） C4 延时差为混合状态 （0，0.4，1.5，3.2，3.3） ]

应用贝叶斯滤波信道估计算法对接收到的信号展开处理。同时，记录不同信噪比（SNR）和不同信道条件下所提方法的MSE性能，结果如图1所示。

根据图1可知，在不同信噪比和信道条件下，贝叶斯滤波信道估计算法均能够较为准确地估计出信道状态，且整个过程中MSE随着信噪比的增加而减小，说明本文方法具有较高的适应能力。此外，还可以注意到在高信噪比下，本文方法的性能依然保持稳定，能够为后续的码间干扰时序抑制提供很好的数据支持。

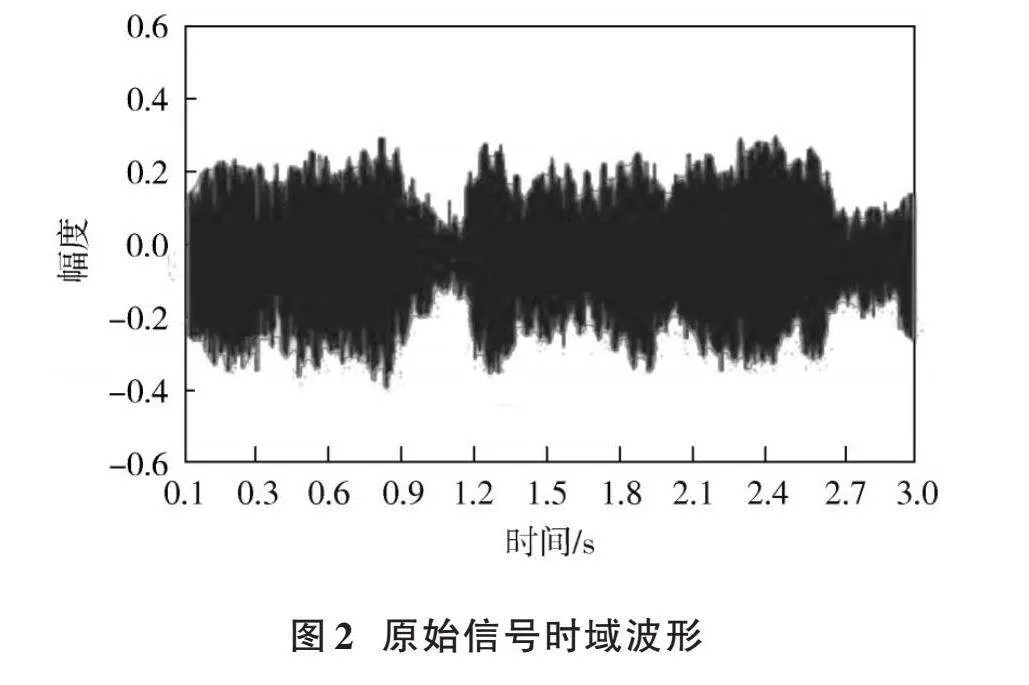
为了验证本文方法采用的无线通信网络码间干扰时序抑制策略的有效性，假设无线通信网络中通信信号的传输频率为2.1 GHz，速率为10 Mb/s，在模拟的多径环境中，设定主径信号延迟为0，其他多径信号模拟不同的延迟和衰减，并与主径信号叠加产生码间干扰。设定多径信号与主径信号之间的功率比为-5 dB，以及多径信号的延迟为260 nm，由此得到的时域波形图如图2所示。

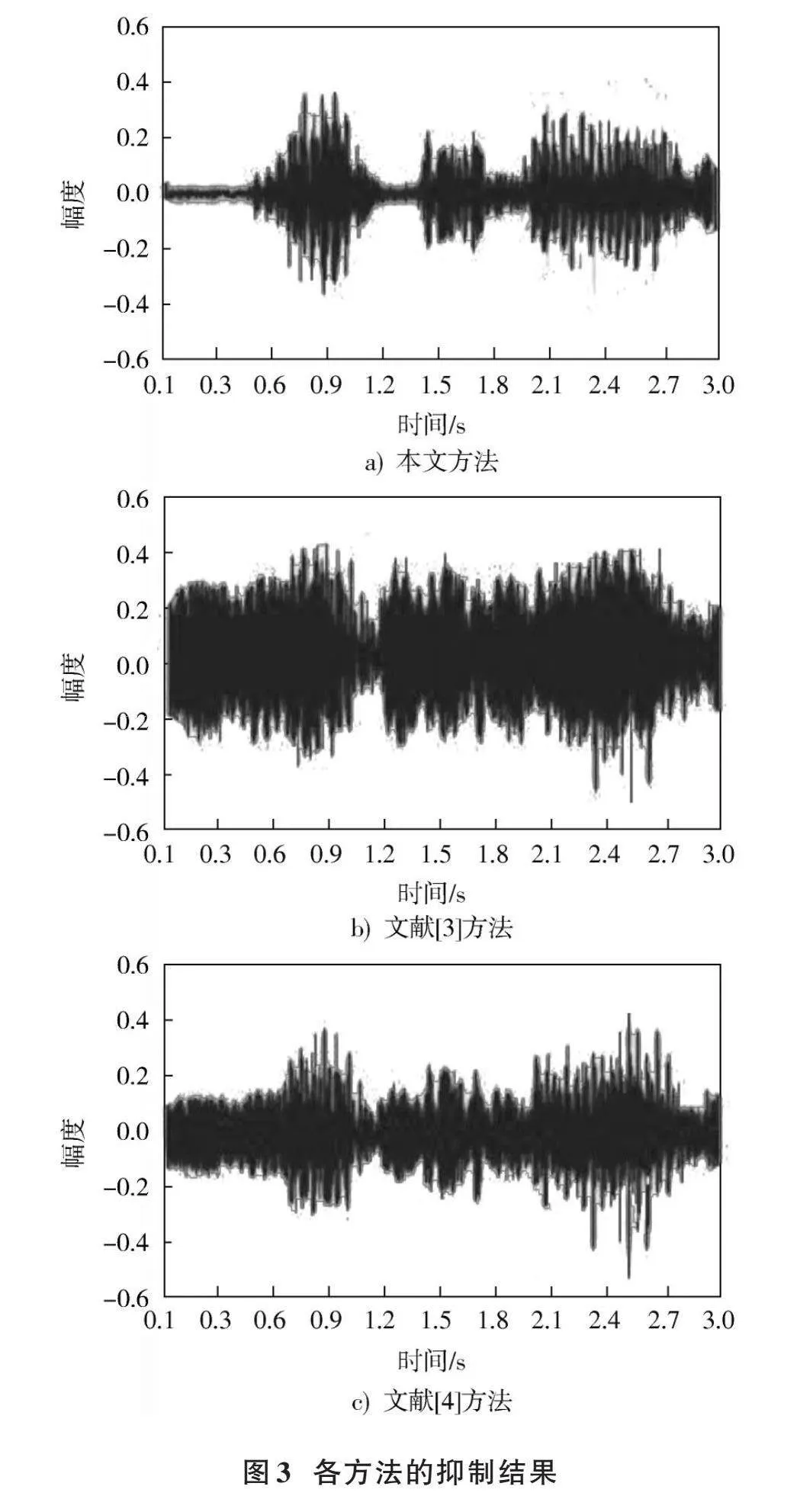
在此基础上，引入文献[3]方法和文献[4]方法与本文方法展开对比，以证明本文方法的优异性，经这三种方法抑制后的波形图变化如图3所示。

根据图3可知，本文方法能够显著减少码间干扰的影响，使信号波形更加清晰和接近原始信号（见图2），也表明本文方法能够有效地抑制码间干扰，提高信号质量。与之相比，文献[3]方法和文献[4]方法在抑制码间干扰方面表现较差。它们的抑制结果中仍存在较明显的码间干扰痕迹，信号波形不够清晰。这可能是因为这两种方法在处理多径信号和码间干扰时存在一定的局限性或不足。

以干扰抑制比[ϕ]和信号失真度[ε]作为衡量上述三种方法性能的评估指标，计算公式为：

[ϕ=10lgσ2σ2ε=10lgσ0-σ2σ02]" "（15）

式中：[σ]、[σ]表示码间干扰抑制前和抑制后的信号。

当[ϕlt;]30 dB且[ε]低于-20 dB时，说明无线通信网络的通信信道信号码间干扰抑制效果已经达到预期。

在不同信道环境下的结果如表2所示。

根据表2可知，在多种不同的信道环境下，本文方法无论是在多径且低延迟的信道A，还是在多径且高延迟的信道B，干扰抑制比均超过30 dB，且信号失真度低于-20 dB；相比之下，文献[3]方法在相同的信道环境下的性能均不如本文方法，干扰抑制比较低，且信号失真度较高；文献[4]方法的两项指标值波动较大，说明这两种方法在抑制码间干扰方面存在一定的局限性和不稳定性。

4" 结" 语

为了保障无线通信网络的稳定高效传输，避免码间干扰对网络传输过程中产生的影响，本文方法通过建立信道模型、多径特性测量以及信道估计，实时跟踪和分析无线通信网络通信信道的传输模式和行为状态，根据分析结果引入基于模糊集的模糊神经网络盲均衡算法实现码间干扰的时序抑制，降低了在抑制码间干扰方面的局限性和不稳定性，具有重要的实际应用价值。

参考文献

[1] 张天骐，方竹，汪锐，等.窄带干扰及动态环境BOC调制信号多通道并行捕获[J].系统工程与电子技术，2023，45（4）：1222⁃1230.

[2] 缪涛，杜建新，王陈.一种基于正交脉冲整形双相位共轭孪生波的非线性抑制方案[J].光通信技术，2021，45（6）：26⁃30.

[3] 孙琳，李海森，李羿萱.双向干扰抑制的多用户滤波多音水声通信研究[J].华中科技大学学报（自然科学版），2023，51（9）：40⁃47.

[4] GUO Q， JIANG H Y， XIANG J H， et al. OTFS narrowband interference suppression based on energy concentration [J]. Digital signal processing， 2024， 149： 104489.

[5] 毕英杰，李森.基于最大相关熵准则的恒模盲均衡算法[J].信号处理，2020，36（1）：118⁃124.

[6] 李萌，孙艺夫，安康，等.非理想信道状态信息下RIS辅助的安全通信[J].电讯技术，2023，63（7）：1017⁃1027.

[7] 唐子翔，吕方旭，师剑军，等.面向高信道衰减的低功耗112 Gibit/s Duo⁃binary PAM4 SerDes发射机设计[J].电光与控制，2022，29（11）：82⁃85.

[8] 赵林仙，赵峰，杨雄伟，等.灵活高阶正交幅度调制矢量光信号的产生与传输分析[J].激光与光电子学进展，2023，60（5）：94⁃101.

[9] 宗樱，孙艳楠，冯强，等.分段Chirp傅里叶变换快速算法[J].扬州大学学报（自然科学版），2023，26（3）：43⁃49.

[10] 云双星，徐红伟，付宁，等.基于傅里叶系数实部的脉冲流信号欠Nyquist采样方法[J].电子与信息学报，2023，45（6）：2153⁃2161.

[11] 李新东，王娟，冯宗鑫，等.自适应增益光电探测电路设计[J].红外技术，2024，46（1）：12⁃19.

[12] 许召召，申德荣，聂铁铮，等.融合信息增益比和遗传算法的混合式特征选择算法[J].软件学报，2022，33（3）：1128⁃1140.

[13] 郑天，李峰，罗印升，等.基于高斯核函数的Hammerstein非线性系统辨识[J].控制工程，2022，29（11）：2034⁃2041.

[14] 苗轶如，宋鹏云，吕铭晟，等.表贴式永磁同步电机预测转矩控制的无权重代价函数设计方法[J].电工技术学报，2023，38（12）：3141⁃3150.

[15] 沈显照，杨鹏程.一种频域脉冲最小均方误差杂波对消算法[J].雷达科学与技术，2023，21（2）：151⁃156.

[16] 马煜.多链路即时通信干扰信号广域监测系统设计[J].电子设计工程，2023，31（11）：138⁃142.