饱和地基多排孔列近场主动隔振问题的半解析BEM并行优化算法分析

摘要： 人工振动污染在国际上已被列入“七大环境公害”之一，多排孔列隔振是振动污染治理的一种方式。针对饱和地基中多排孔列近场主动隔振问题，基于饱和土半解析边界元法（BEM），分别建立了动力机器基础的环境振动影响和多排孔列近场隔振的边界元方程。为提高BEM计算效率，构建了饱和土半解析BEM的SPMD（单程序多数据）并行算法，同时利用孔列间在空间上的对应关系提出了边界元影响系数矩阵快速生成的优化算法。在此基础上，深入研究了多排孔列的近场主动隔振效果，分析了布孔方式、几何参数和多排孔距振源距离对其隔振效果的影响。结果表明：饱和土半解析BEM的SPMD并行算法结合影响系数矩阵生成的优化算法可显著提升多排孔列隔振问题的计算效率。多排孔列的布孔方式对隔振效果基本无影响；增加排孔孔数和孔径、降低孔间净距均能取得更好的隔振效果，而多排孔的排数和排间距对隔振效果影响相对不大；随着多排孔距振源距离增加，多排孔隔振效果先提高后趋于稳定。在实际工程设计时，建议多排孔排数宜为两排，排孔孔径取0.15（为Rayleigh波波长）、孔深取、孔间净距取0.1，单排孔数宜根据所需屏蔽区域的面积合理确定。

关键词： 饱和地基； 动力机器基础； 地面振动； 多排孔； SPMD； 隔振效果

中图分类号： TU435""" 文献标志码： A""" 文章编号： 1004-4523（2025）01-0054-14

DOI：10.16385/j.cnki.issn.1004-4523.2025.01.007

Vibration isolation of multi-row of holes as active barriers in saturated soil using semi-analytical BEM with parallel optimization algorithms

SHI Gang， ZHANG Hao， Gao Xinjun

（School of Civil Engineering， Zhengzhou University， Zhengzhou 450001，China）

Abstract： In modern daily life， people are often exposed to many types of vibrations generated by machine operations， traffic and other human activities. These vibrations can cause annoyance to residents， and even interfere the operations of precision instruments. Generally， these adverse effects of vibrations can be eliminated or prevented by installation of various types of wave barriers， such as multi-row of holes. In the paper， the investigation is focused on effects of using multi-row of holes for the reduction of nearby vibration response generated by dynamic machine foundation laid on saturated soil. Two semi-analytical BEM models are established to calculate the environmental vibrations due to the machine foundation and the vibration isolation efficiency by multi-row of holes， respectively. In order to increase calculating efficiency of the semi-analytical BEM， a simple SPMD parallel algorithm is developed using Matlab software. The SPMD parallel algorithm is optimized by using the corresponding relationship between holes on the spatial coordinates. By using the optimized SPMD parallel algorithm， the effects of the model parameters on effectiveness of vibration isolation are calculated and discussed in detail. The results show that the optimized SPMD parallel algorithm of semi-analytical BEM is much faster than the chained program dramatically. Multi-row of holes can isolate the ground vibrations successfully， and the holes layout has less effect on the screening efficiency. Increasing the radius and the number of holes in a row， decreasing the net spacing between two successive holes can all lead to an increase in the screening effectiveness， while the rows of holes and the net spacing between two successive rows have less effect on the screening effectiveness. Further， the distance between the rigid foundation and wave barriers can has a limited impact on vibration mitigation effectiveness. According to the results， it’s suggested in the design that two-row of holes is recommended and the hole depth， radius and the nest spacing between two successive holes should take the values of 1.0， 0.15 and 0.1， respectively.

Keywords： saturated soil；machine foundation；ground vibrations；multi-row of holes；SPMD；vibration isolation" effectiveness

在城市中，大型机械运行、车辆行驶等会产生环境振动污染，对邻近居民的日常生活、精密仪器设备运行等产生负面影响。国际上已把振动污染列为“七大环境公害”之一。因此，人工振动污染的治理就成为当前急需解决的重要课题之一。在地基中设置隔振屏障是振动污染治理的一种有效方法^［1］，特别适合对已建成地铁等振动污染的治理以及对已建成房屋建筑的振动防护。其中，工程中常用的非连续屏障包括排孔和排桩，由于排孔设置较简单，还可在孔内设置橡胶气囊等保持孔壁稳定，其在工程中有较多应用。

国内外众多学者对排孔隔振问题进行了研究。在试验研究方面，WOODS等^［2］采用全息照像技术对孔列的隔振效果进行了研究；LIAO等^［3］采用水波比拟法进行了水中孔列隔振的比例模型试验；丁松波等^［4］对地铁车站基坑爆破施工中排孔的减振效果进行了现场实测分析。在理论研究方面，徐平等^［5‑7］采用波函数展开法分别研究了单排、多排空心管桩、多排柱形空腔对入射弹性波的隔振问题。在数值模拟方面，TSAI等^［8］采用三维BEM研究了空心管桩对基础竖向振动的隔振效果；欧阳圳等^［9］采用弹性半解析BEM研究了Rayleigh波入射时孔列的隔振效果；丁文湘等^［10］采用有限元法分析了强夯加固地基时孔列的隔振效果。针对饱和土地基孔列隔振问题，李校兵等^［11］采用波函数展开法研究了单排孔列对快纵波的隔离问题；时刚等^［12］采用饱和土半解析BEM研究了多排孔列对入射Rayleigh波的远场被动隔振问题。此外，孙连勇等^［13］对饱和地基中单排孔近场主动隔振问题进行了现场试验和数值模拟分析。

孔列隔振是一个半空间波动问题，边界元法由于其采用的Green函数能够自动满足波动的无穷远辐射条件，特别适合半空间域波动问题的求解。然而，边界元法所形成的影响系数矩阵是非对称满秩矩阵，大规模问题的计算量巨大，其量级为，限制了边界元法在大规模问题中的应用。此外，饱和土BEM采用的Green函数^［14］较弹性边界元法的Green函数^［15］更为复杂，计算效率较低；采用半空间基本解作为Green函数^［16］可大大减少所分析问题的自由度数量，可在一定程度上提高计算效率。除上述方法外，目前并行计算成为大规模科学和工程计算的一个重要发展方向。SYMM^［17］最早在分布式阵列处理机系统上实现了并行求解Dirichlet问题；DAVIES^［18］对系数积分并行性进行了研究；尹欣^［19］则在网络机群环境下完成了三维弹性静力学问题的并行计算；雷霆等^［20］实现了三维弹性力学快速多极边界元的并行计算；张健飞等^{［21‑22］}分别研究了边界元子域并行算法和集群并行环境下弹性静力问题的边界元并行算法；王英俊等^［23］、张锐等^［24］分别研究了三维弹性静力学和大规模声学边界元法的GPU并行算法。上述并行算法多针对Green函数形式简单、边界节点数量庞大的情况，通过划分计算子域等方法来实现并行计算，并行算法程序编制难度较大，不适合解决Green函数形式复杂而边界节点数量不大的问题。

针对饱和地基明置动力机器基础环境振动影响的多排孔列近场主动隔振问题，本文基于饱和土半解析BEM建立了多排孔列对动力机器基础振动影响近场隔振的边界元方程；为提高计算效率，提出饱和土半解析BEM的SPMD并行算法，并利用孔列在空间上的对应关系建立了边界元影响系数矩阵快速生成的优化算法；在此基础上对多排孔列近场主动隔振效果进行了详细的参数分析。

1 饱和地基多排孔近场主动隔振的半解析边界元分析

动力机器基础在荷载作用下产生振动，在地基中产生弹性波，弹性波沿地基向周边传播，从而对周边环境造成振动污染。为降低振动污染，可在动力机器基础周边设置屏障进行隔振，这种隔振方式即为近场主动隔振。

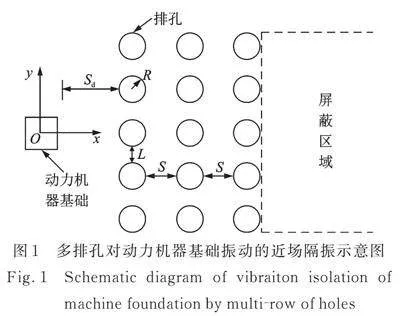
饱和地基多排孔列对动力机器基础振动影响的近场隔振问题如图1所示。图中，S为排间距，S_d为屏障距动力机器基础距离，R为孔径，L为相邻孔间净距。

本文采用饱和土半解析BEM^［16］分析多排孔列近场隔振问题，首先计算在集中荷载和力矩作用下动力机器基础对周边环境产生的地面振动；在此基础上，计算设置多排孔列后动力机器基础产生的地面振动；最后，对设置多排孔前、后的地面振动进行对比，最终获得不同位置处的隔振效果。

1.1 饱和土半解析边界元法

对于饱和多孔介质（后文简称饱和土）的波动问题，考虑稳态振动形式，以土骨架位移和孔隙压力表示的Biot波动方程为^［14］：

（1）

式中，； 和为土骨架的Lame常数；为Biot有效应力系数；表示对i向坐标求导；为饱和多孔介质材料常数；为饱和土的孔隙率； 为饱和土体积密度，其中，和分别为土骨架密度和流体密度；为土体渗透系数；为饱和土附加质量密度；，分别为作用在土骨架上和流体上的体积力；为作用在流体上的源项。

饱和土的边界积分方程可表示为^［14］：

（2）

式中，、、、表示与相对应的Green函数；而、、、则表示与相关的Green函数；∮表示柯西主值积分；自由项和是由边界几何条件决定的常数；为三维空间域的边界；为面力；为流量。

为求解式（2），采用类似于有限元离散方法对边界积分方程进行离散求解，这就是饱和土边界元法^［14］。常规饱和土边界元法一般采用全空间动力Green函数，求解半空间波动问题时，需要在半空间表面划分边界单元。为降低自由度数量，可采用薄层法（TLM）计算得到饱和半空间的动力Green函数^［25］，这就是饱和土半解析边界元法^{［12‑13，16］}。

考虑到孔列边界为圆柱面，本文边界单元采用二次单元。进行边界元计算时，采用二次退化单元法消除弱奇异性积分；而对于强奇异性积分，采用文献［26］提出的非线性变换方法进行消除。

1.2 动力机器基础振动的半解析边界元方程

对图1所示的明置基础，假定基础为刚性体，其上作用3个集中荷载，，和2个力矩，。为简化表述，下文中省略。

动力机器基础的半解析边界元方程为^［13］：

（3）

式中，和分别为刚性基础‑饱和地基交界面的位移和面力向量；和分别为刚性基础的荷载向量和位移向量；为刚性基础‑饱和地基交界面的边界元影响系数矩阵，需要通过对边界单元进行积分得到；为惯性矩阵；为位移转换矩阵。

饱和地基振动的半解析边界元方程可表示为：

（4）

式中，下标“f₁”表示饱和地基‑刚性基础交界面的边界元节点；，分别为交界面上位移、孔压向量；，分别为面力、流量向量；和分别为位移孔压影响系数矩阵和面力流量影响系数矩阵。

根据饱和地基‑刚性基础交界面的连续条件和平衡条件，有：

（5）

式中，为刚性基础‑饱和地基交界面的法向量矩阵。

式（3）和（4）可根据式（5）给出的边界条件耦合在一起，即可得到明置刚性基础的振动方程：

（6）

式中，和分别为零矩阵和单位矩阵。

求解式（6）可得到饱和地基‑刚性基础交界面上的未知量和刚性基础的位移向量。

为得到饱和地基表面任意一点的振动，可采用“内点”的边界积分方程，计算各“内点”的位移和孔压：

（7）

式中，为饱和地基表面计算点的坐标向量；，分别为动力机器基础振动在计算点处产生的位移和孔压。

1.3 多排孔列近场主动隔振的半解析边界元方程

采用饱和土半解析BEM分析多排孔列对动力机器基础振动影响的近场隔振问题时，除在饱和地基‑动力机器基础交界面上进行边界单元划分外，还需要在排孔内表面上进行边界单元划分。此时，饱和地基振动的边界元方程可表示为：

（8）

式中，下标“f_a”“f₂”分别表示全部边界元节点和孔列内表面边界元节点；其他符号含义同上文。

考虑孔列内表面不透水的情况，则孔列内表面的边界条件可表示为：

， （9）

式中，为孔列内表面的法向量矩阵。

式（3）和（8）可根据式（5）和（9）给出的边界条件进行耦合，整理后可得多排孔列对动力机器基础振动影响近场隔振的边界元方程为：

（10）

求解式（10）可得到饱和地基‑刚性基础交界面和孔列内表面未知量以及刚性基础位移向量。

设置多排孔列后，饱和地基表面任意一点的振动位移采用与式（7）类似的方法计算，此时，式（7）中下标为“f_a”。

为评价多排孔列的隔振效果，引入竖向位移振幅衰减系数和平均竖向位移振幅衰减系数，具体定义可参考文献［13］，此处不再赘述。

2 饱和土半解析BEM并行算法及多排孔列隔振时的算法优化

对于多排孔列近场主动隔振问题，随着孔列数量的增多，边界元影响系数矩阵的元素数量成倍增加，串行算法计算耗时过长，难以满足大规模计算需求，亟需开发合适的并行算法来降低计算耗时。

2.1 饱和土半解析BEM并行计算的思路

饱和土半解析BEM^{［12‑13，16］}采用薄层法（TLM）计算得到的饱和半空间动力Green函数，影响系数矩阵的元素总数量相对较少，但单个元素的计算涉及大量的矩阵乘法运算^［25］，使得影响系数矩阵的计算量一般可占到总计算量的95%以上，耗时较长。因此，进行并行算法设计时，不需要像边界元子域并行算法^{［21‑22］}一样进行计算子域的划分，只需将影响系数矩阵的计算过程进行并行化即可。

形成影响系数矩阵的计算可分为三层循环：边界元节点循环、边界单元循环和Gauss积分点循环。其中，按边界元节点循环形成的影响系数矩阵表示如下：

（11）

式中，表示第j个边界节点作为源点时的影响系数子矩阵，其中，为第j个节点坐标向量；表示边界节点j对边界节点i的影响系数子矩阵。

由边界元理论^［15］可知，的计算生成与的计算生成是相互独立的，但计算过程相同，仅源点坐标不同。因此，饱和土半解析BEM可在边界元节点循环层进行并行计算，无需对计算区域进行子域划分，采用简单的并行算法（循环并行化）即可实现饱和土半解析BEM的并行计算，即对原串行程序进行边界节点循环计算过程的并行化即可实现并行计算，编制难度较低。

2.2 饱和土半解析BEM并行算法设计与实现

2.2.1 并行算法程序的设计

目前常用的并行程序模型中，共享变量模型^［27］可实现松散同步、多线程处理（SPMD、MPMD），是一种应用广泛的并行编程模型。根据2.1节分析，饱和土半解析BEM适合采用共享变量模型的SPMD（单程序多数据）来实现并行计算，即在每个计算核上运行相同的程序，通过给每个计算核分配不同的循环变量值（不同源点坐标值）来完成影响系数矩阵的并行计算。从上述分析来看，饱和土半解析BEM是易并行的。

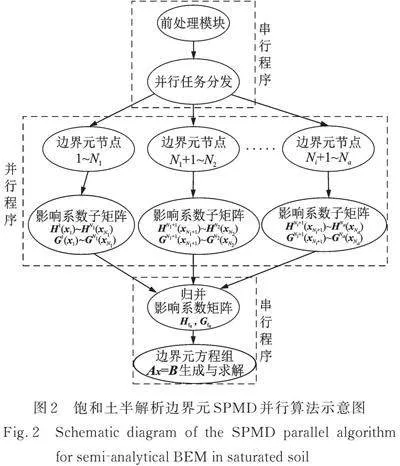
饱和土半解析BEM的计算过程可分为四个部分：①前处理：生成边界元网格信息，输入材料参数、初始条件和边界条件；②边界元影响系数矩阵计算；③边界元方程组生成和求解；④“域内点”未知量计算。上述过程中，过程①耗时极少，适合串行处理；过程②应采用SPMD并行计算；过程③由于半解析BEM的边界节点数量较少而计算耗时较短，也适合采用串行处理；对过程④，当“域内点”数量较多时，与过程②一样也应采用SPMD并行计算。

按上述分析，饱和土半解析BEM并行算法可按图2进行设计，通过任务分发来实现边界元影响系数矩阵的并行计算，通过归并形成完整的影响系数矩阵。

2.2.2 并行算法程序的实现

本文采用数学软件Matlab的SPMD并行结构^［28］对饱和土半解析BEM进行并行算法设计。在Matlab的SPMD并行结构中，可以将串行程序与并行程序组合在一起，串行程序在客户端Matlab上执行，除负责边界元前处理和边界元方程组的生成与求解外，还负责任务分发和影响系数矩阵的归并；SPMD并行程序在多个处理单元（Matlab中称之为lab）上执行，每个lab负责节点N_i～N_j影响系数子矩阵的计算。

Matlab并行结构编程中，需要解决并行计算任务的分发和影响系数矩阵的存储与归并问题。计算任务的分发采用composite变量^［28］，这个变量可在不同的lab上取不同的值。编程时，可定义两个composite变量，其在每个lab上的值为该lab负责计算的边界元节点的起始与结束编号，从而实现并行任务的分发。影响系数矩阵的存储与归并采用distributed列阵（分布式阵列）^［28］实现。distributed阵列在逻辑上是一个整体，但组成阵列的数据被分配到各个lab中，每个lab中仅拥有一部分数据。通过distributed阵列，可方便地实现影响系数矩阵的归并，减少各lab与串行主程序间的通讯消耗。

2.3 多排孔列近场隔振并行计算的算法优化

对于多排孔列近场主动隔振问题，当孔列总数目较多时，采用SPMD并行算法仍需要消耗较长的时间生成边界元影响系数矩阵。为提高计算效率，可根据多排孔列中各个孔在空间上的对应关系，结合边界元基本原理对并行算法进行优化，消除影响系数矩阵元素生成过程中的重复性计算消耗。

2.3.1 单排孔近场隔振问题的算法优化

以影响系数矩阵为例，假定n个孔的单排孔列，可表示为：

（12）

式中，表示明置基础‑饱和地基交界面边界节点

的影响系数子矩阵；表示明置基础‑饱和地基交界面边界节点对第i个孔边界节点的影响系数子矩阵；表示第i个孔边界节点对明置基础‑饱和地基交界面边界节点的影响系数子矩阵；表示第i个孔边界节点对第j个孔边界节点的影响系数子矩阵。

式（12）中的影响系数矩阵可分成3个子块计算，具体如图3所示。

影响系数矩阵各分块的计算策略如下：

①对分块1，边界单元循环计算时，只需对边界“f₁”的单元进行循环，无需对边界“f₂”的单元进行循环，直接采用前述并行算法即可。

②对分块2，由于“f₁”边界节点数量很少，可采用前述并行算法或串行算法直接计算。

③对分块3，当桩孔数目较多时，分块3的计算大概能占全部计算量的95%以上，且存在大量的重复性计算，有必要进行算法优化。根据BEM理论^［15］，影响系数的计算仅与源点和场点的相对位置以及场点的边界面法向量有关。对于孔列隔振，通常各个孔的几何尺寸（网格划分）和相邻孔间净距均相同，因此，第i个孔的边界节点m对第j个孔边界节点的影响系数子矩阵，与第i+1个孔的边界节点（与节点m位置相同）对第j+1个孔边界节点的影响系数子矩阵应相等。由此可知，第i个孔的全部边界节点对第j个孔边界节点的影响系数子矩阵，与第i+1个孔的全部边界节点对第j+1个孔边界节点的影响系数子矩阵相等。

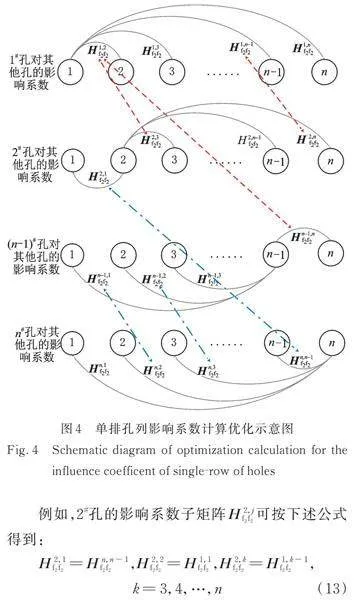
单排孔列各个孔之间的对应关系如图4所示。算法设计时，可只计算1^#孔的影响系数子矩阵和n^#孔的影响系数子矩阵，其中，j取1～n。分块3中的其他影响系数子矩阵均可由这两个孔的影响系数子矩阵得到。

例如，2^#孔的影响系数子矩阵可按下述公式得到：

，，，

（13）

其他各孔的影响系数子矩阵可按式（13）类似方法获得，这样就消除了影响系数矩阵中的大量重复性计算，从而大大减少了计算耗时；孔列数目越多，计算效率的提升就越显著。

2.3.2 多排孔列近场隔振问题的算法优化

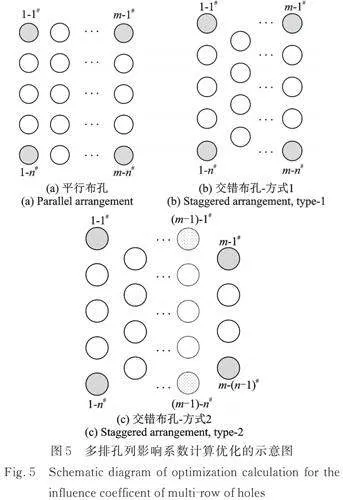
多排孔列近场隔振问题可参照单排孔列的算法优化方法进行，但需要考虑孔列在空间上不同布置问题。m排孔列（平行布孔时，每排孔数为n；交错布孔时，奇数排孔数为n，偶数排孔数为n-1）可划分成3种排列形式，如图5所示。

算法优化时，平行布孔方式（如图5（a）所示）和交错布孔方式1（奇数排布孔，如图5（b）所示）可只计算第1排1‑1^#孔和1‑n^#孔、第m排的m‑1^#孔和m‑n^#孔的影响系数子矩阵，其他孔影响系数子矩阵均可由上述4个孔的影响系数子矩阵根据孔列对应关系获得。交错布孔方式2（偶数排布孔，如图5（c）所示）除需要计算第1排1‑1^#孔和1‑n^#孔、第m排的m‑1^#孔和m‑（n-1）^#孔的影响系数子矩阵外，尚需要额外计算第m-1排的（m-1）‑1^#孔对1‑n^#孔和（m-1）‑n^#孔对1‑1^#孔的影响系数子矩阵，其他孔影响系数子矩阵均可由上述影响系数子矩阵根据对应关系获得。

在程序编制时，引入孔‑孔定位向量，例如，第i个孔对第j个孔的定位向量定义为：

（14）

式中，、分别表示第i个孔和第j个孔中心点x向坐标；、则为孔中心点的y向坐标。

引入式（14）所示的孔‑孔定位向量后，首先按照图5列出的排孔位置生成相应的孔‑孔定位向量，采用并行算法计算“计算孔”（图5中的灰色孔）的影响系数子矩阵。生成剩余孔（下称“生成孔”）的影响系数子矩阵时，就可根据“生成孔”对其他各孔的定位向量，依次在“计算孔”‑其他孔定位向量集中进行检索，当两定位向量相同时，完成对应性的检索，按照类似于单排孔列影响系数子矩阵的对应关系方法，最终获得“生成孔”对其他孔的影响系数子矩阵。

3 算法验证与计算效率分析

3.1 算法验证

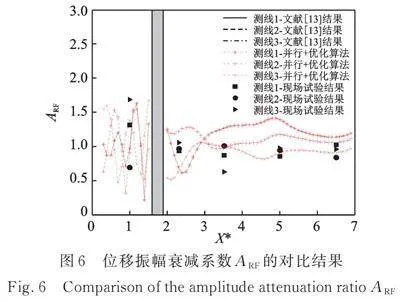
为验证本文并行+优化算法程序的正确性，对文献［13］中单排孔列近场隔振的现场试验进行了模拟。现场试验工况为：激振频率150 Hz，浅层土体Rayleigh波波速150 m/s；采用单排孔列隔振，孔数为5；孔半径（为Rayleigh波波长），孔深，相邻孔间净距，距激振源距离。计算结果如图6所示，同时给出了现场试验结果以及文献［13］中串行程序的计算结果。

由图6可知，在单排孔前方，本文计算结果与现场试验结果吻合相对较好；而在单排孔后方，测点1‑3^#、测点1‑4^#的误差相对较大，其他测点与计算结果偏差相对不大，本文计算结果基本能够反映现场试验规律。此外，本文计算结果与文献［13］串行程序计算结果一致，这表明对于排孔隔振问题，本文建立的并行+优化算法程序是正确的。

实际上，无论是并行算法，还是并行+优化算法，本质上并未改变边界元影响系数矩阵的计算方法。并行算法仅仅是将对边界元节点的循环计算拆分成多个分段循环在不同计算核心上并行运行；而并行+优化算法则是利用孔列之间在空间几何关系上的对应性来消除影响系数矩阵中的重复性计算，非重复计算部分仍采用与串行程序相同的计算过程计算。

3.2 饱和土半解析BEM并行算法的效率分析

为考察饱和土半解析BEM并行算法的计算效率，对饱和地基中单排孔隔振问题进行了计算，分析计算核心数量（lab数量）和边界元节点数量（计算规模）对并行计算效率的影响。

为衡量并行算法的计算效率，定义效率^［27］：

（15）

式中，、分别为串行程序和并行程序的计算耗时；为计算核心数量。

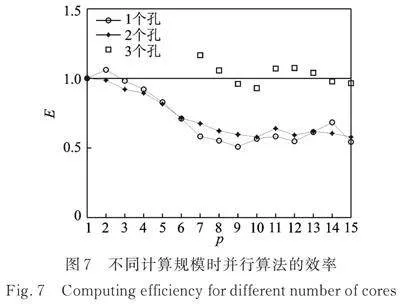
分别采用串行程序和SPMD并行程序对单排孔隔振问题进行计算分析，按式（15）计算并行程序的效率，结果如图7所示。其中，考虑到串行程序计算耗时较长，采用了较少孔数的单排孔。

由图7可知，当计算规模较小（1个孔）时，计算核心数量较少时效率较高，接近于1；随着计算核心数量的增加，效率逐渐降低并稳定在0.6左右。当计算规模较大时，效率大体稳定在1.0左右，说明本文并行算法效率较高。分析其原因，在饱和土半解析BEM中，除边界节点、单元信息以及材料参数外，薄层法Green函数中特征值及特征向量矩阵都需要从客户端传递给各lab，计算规模增加时，传递的信息没有明显增加。应当注意，由于本文衡量效率E的方法比较简单，且Matlab计算耗时受系统配置、版本等因素影响存在一定误差，使得效率出现超过1的情况。

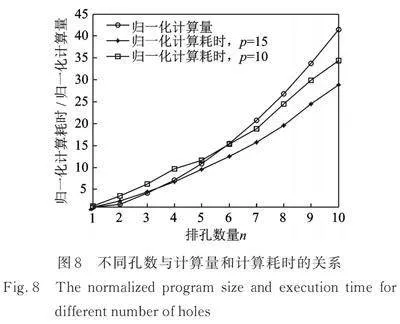
此外，为考察计算规模（孔列数目）增大时并行算法计算耗时的情况，对不同孔数单排孔隔振问题的计算耗时与计算量关系进行了分析，结果如图8所示。其中，计算量定义为边界节点数×边界单元数+“域内点”数×边界单元数，计算耗时和计算量均以1个孔的工况为基准进行归一化处理。由图8可知，当计算规模较小时（桩孔数lt;4），随着计算量的增加，计算耗时也随之增加，两者增加的幅度相差不大；随着计算规模的增加（孔列数gt;4），计算耗时的增加幅度远小于计算量的增加幅度，这表明当计算规模较大时，并行算法具有更高的效率，用于协调并行程序的工作所需时间占比越来越小。

3.3 多排孔列隔振问题并行优化算法的效率分析

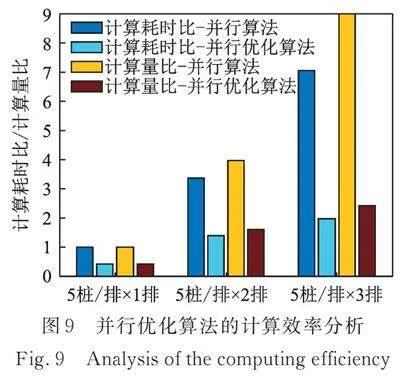
为考察多排孔近场隔振问题并行优化算法的计算效率，分别对单排孔和多排孔近场隔振问题进行了计算。计算工况为：排孔孔深，孔径，相邻孔间净距，排间距；排数分别取1，2和3排，每排孔数为5。分别采用并行算法和并行优化算法进行计算，结果如图9所示。其中，计算耗时比和计算量比均以单排孔并行算法为基准量，计算量则采用影响系数矩阵元素数目进行衡量。

由图9可知，对于并行算法，随着孔列排数的增加，计算量呈增长，而计算耗时增幅则稍低于；采用并行优化算法时，其计算量增幅远低于，计算耗时增幅稍低于计算量的增幅。对比两种算法可发现，并行优化算法能显著降低影响系数矩阵的计算耗时，影响系数矩阵的生成时间约为并行算法耗时的4/N（N为总孔数）左右，显著提高了程序的计算效率。

由上述分析可知，针对多排孔列近场隔振问题提出的并行优化方法能够显著提高饱和土边界元算法的计算效率，大大减少了计算耗时，且程序修改难度较低。结合多排孔列隔振问题分析可知，该算法适合于所分析问题中存在数量较多的“基本结构”，例如，屏障隔振问题中的单排/多排孔列、单排/多排桩列，其中，孔或桩均可视为“基本结构”，采用上述算法可大大减少影响系数矩阵生成过程中的大量重复性计算，提高了计算效率。此外，对于一些规则结构体系，也可通过人为划分“基本结构”的方法来提升计算效率；但应注意，划分“基本结构”时会大大增加边界元前处理的难度，应根据分析对象的不同慎重选择。

4 多排孔近场主动隔振的参数分析

采用饱和土半解析BEM并行优化算法对多排孔列近场主动隔振问题进行计算。研究时，主要考虑相邻孔间净距、排间距以及排孔孔深、孔径、排孔数量（，分别表示奇数排和偶数排）、排数和屏障距动力机器基础距离对隔振效果的影响。几何尺寸均采用无量纲化参量表示，即无量纲孔间净距、无量纲排距、无量纲孔深、无量纲孔径和距基础的无量纲距离。

基准条件下计算参数如表1所示。

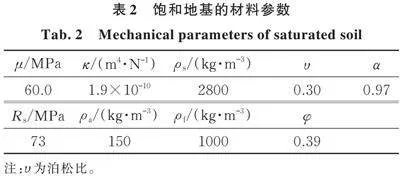
饱和地基材料参数如表2所示。

本文研究采用单因素分析法，即考虑一种因素影响时，其他参数不变。

4.1 多排孔列布设方式的影响

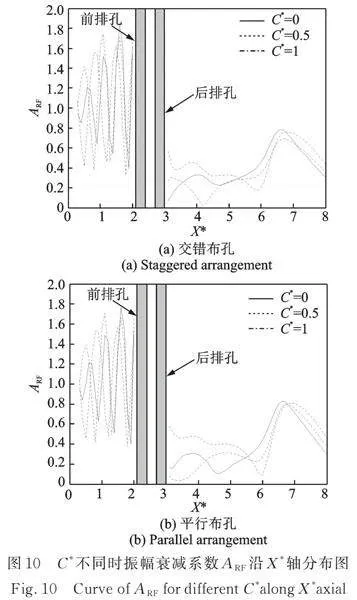
为分析多排孔列布设方式（平行布设和交错布设）对其隔振效果的影响，分别对两种布孔方式进行计算分析，计算结果如图10所示。

图10为不同时振幅衰减系数沿轴的变化曲线。其中，为距屏障中心纵轴线的距离与屏障宽度一半的比值，屏障边缘处，屏障中心处。由图10可知，屏障后地面振幅衰减系数，表明多排孔列能够有效地对动力机器基础产生的地面振动进行隔振。对比交错布孔和平行布孔两种方式，屏障后紧靠屏障的位置，两种布孔方式的隔振效果稍有差别，但随着距屏障距离的增加，两种布孔方式的隔振效果基本相同，这与多排孔远场隔振结论相一致^［12］。

此外，屏蔽区域内呈一定的波动起伏变化，紧靠屏障的区域隔振效果相对较好，而在距多排孔列约的区域，值相对较大，表明该区域屏障隔振效果较差，工程设计时应注意避让该区域。

综上所述，设置多排孔列能够有效地对动力机器基础产生的地面振动进行隔振，多排孔列两种布孔方式的隔振效果基本相同。鉴于此，下文计算分析时均采用交错布孔方式。

4.2 多排孔列几何参数的影响

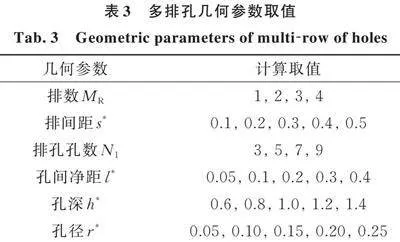
进行多排孔隔振效果的参数分析时，多排孔几何参数取值如表3所示。

4.2.1 多排孔列排数的影响

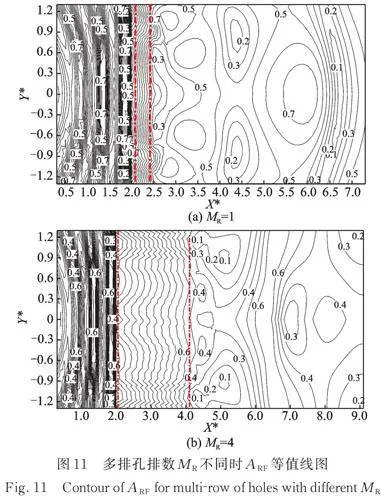
多排孔列的排数是影响多排孔列工程造价的一个关键因素，排数越多，隔振体系的工程造价就越高。多排孔列排数对多排孔列隔振效果影响的计算结果如图11和12所示，其中，图11中两条点划线之间的区域为多排孔列布设区域。

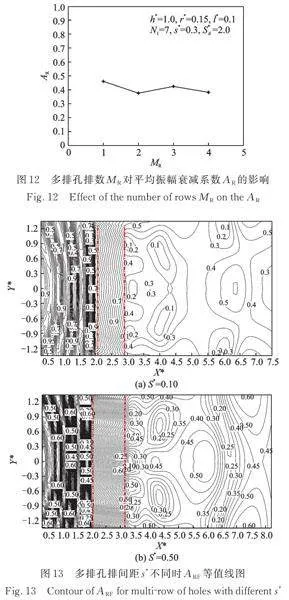
由图11可知，多排孔列的排数不同时，屏障后屏蔽区域内振幅衰减系数的分布规律稍有区别，但差别相对不大：屏障后屏蔽区域的振幅衰减系数在边缘较大而在1/4屏障宽度位置较小，即屏障中心不总是隔振效果最好的区域。由图12可知，随着多排孔列排数的增加，多排孔的平均隔振效果有所提高，但提高幅度不大。因此，工程设计时建议多排孔的排数不超过2排，以节约工程造价和地面空间。

4.2.2 多排孔列排间距的影响

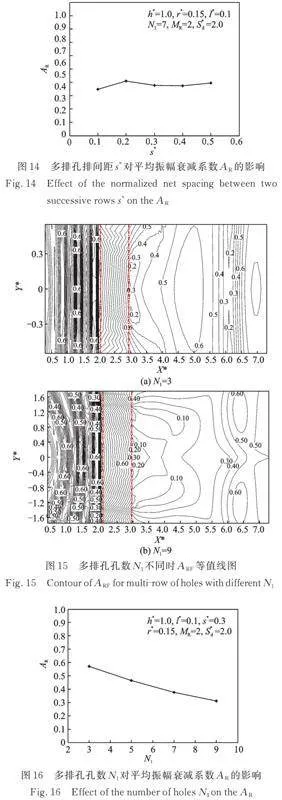
为了分析多排孔列的排间距对其隔振效果的影响，取值如表3所示，计算结果如图13和14所示。

由图13可知，排间距对多排孔后屏蔽区域的振幅衰减系数稍有影响，但这种影响相对不大。由图14可知，当排间距较小时（），多排孔列的平均振幅衰减系数较小，屏障隔振效果较好；随着的增大，多排孔列的隔振效果稍有降低并逐步趋于稳定。

因此，在实际工程设计时，多排孔的排间距不起主要控制作用，可根据排孔的施工技术条件和现场条件确定合理的排间距。

4.2.3 排孔孔数的影响

排孔孔数是影响屏障整体长度的一个关键因素，控制着屏障后屏蔽区域的面积。在分析排孔孔数影响时，第一排排孔数量N₁取值如表3所示，计算结果如图15和16所示。

由图15可知，当孔数N₁较少时，屏障后屏蔽区域的振幅衰减系数呈现出中心区域小、边缘大的现象，表明屏障中心位置的隔振效果相对较好。而当孔数较多时，屏障后的屏蔽区域面积大，且值较小，表明此时多排孔隔振效果相对较好。由图16可知，随着孔数N₁的增加，多排孔列后屏蔽区域的平均隔振效果也随之提高，且提高幅度也较大。这与多排孔远场隔振的结论不同^［12］，产生这种差异性的原因主要是近场隔振时，动力机器基础产生的弹性波波阵面呈球面向四周扩散，而远场隔振则是对入射的平面Rayleigh波进行散射。

综上所述，在实际工程设计时可通过增加多排孔孔数的方法来获得更好的隔振效果和更大的屏蔽区域。

4.2.4 孔间净距的影响

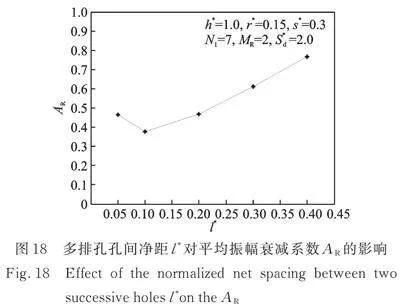
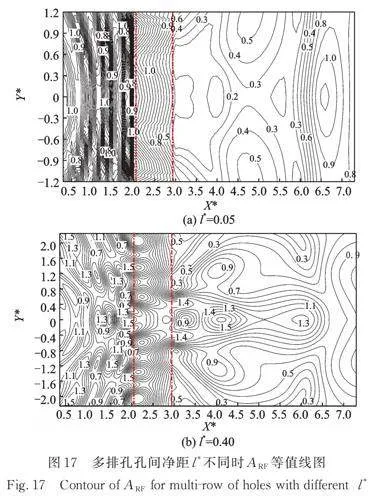
在单排孔隔振问题中，孔间净距是影响隔振效果的关键因素，孔间净距过大时，入射波通过相邻孔之间的间隙入射到屏蔽区域，从而降低屏障的隔振效果^［12］。为分析孔间净距对多排孔列隔振效果的影响，取值如表3所示，计算结果如图17和18所示。

由图17可知，当孔间净距较小时（例如，），多排孔呈一个整体对入射波进行隔振；随着孔间净距的增大，越来越多的入射波通过相邻孔的间隙进入到屏蔽区域内，多排孔的隔振效果逐渐变差，特别是当较大时（），多排孔难以再呈一个整体对入射波进行隔振，而是类似于一个个单独孔进行隔振。由图18可知，当孔间净距较小时，随着的增加，多排孔隔振效果有所提高；当后，多排孔的隔振效果随着的增大而快速劣化。

综上所述，为获得较好的隔振效果，建议多排孔的孔间净距取0.1～0.2。

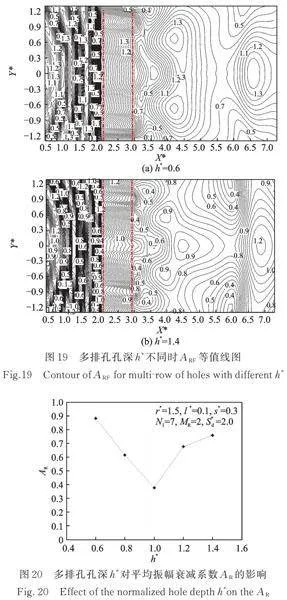
4.2.5 孔深的影响

为分析孔深对多排孔列隔振效果的影响，取值如表3所示，计算结果如图19和20所示。由图19和20可知，对于多排孔隔振而言，当孔深为时，隔振效果最佳，增大或减小孔深均不能获得更好的隔振效果。因此，在工程设计时，建议多排孔列的孔深取。

4.2.6 孔径的影响

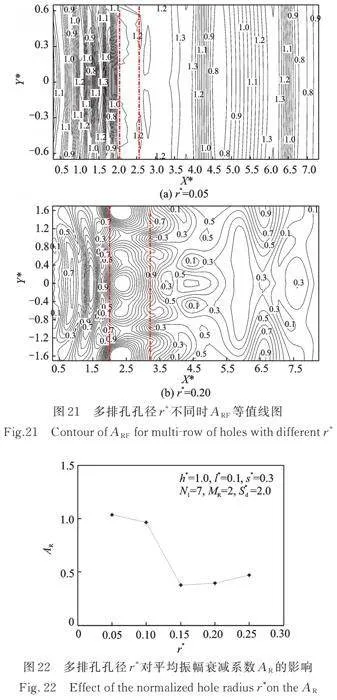
多排孔的孔径也是控制多排孔列隔振效果的一个关键因素。为分析孔径对多排孔列隔振效果的影响，取值如表3所示，计算结果如图21和22所示。

由图21可知，当孔径较小时，屏障隔振效果较差，甚至在屏蔽区域出现明显的振幅异常放大现象，如图21（a）所示。由图22可知，随着孔径的增大，多排孔的平均隔振效果先随之提高，当后，多排孔的平均隔振效果基本不发生变化。

综上所述，在实际工程设计时，考虑到排孔的施工难度和施工成本，建议多排孔的孔径不超过0.15。

4.3 多排孔距动力机器基础距离的影响

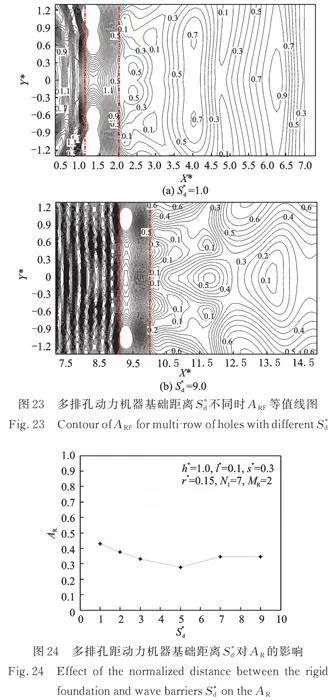
多排孔列的布设位置也是多排孔列近场隔振设计的一个关键因素。为分析多排孔距动力机器基础距离对隔振效果的影响，取值如表3所示，计算结果如图23和24所示。

由图23可知，多排孔列距动力机器基础距离对屏蔽区域的隔振效果有一定的影响，特别是时，屏蔽区域振幅衰减系数的分布规律与其他情况有较大不同。由图24可知，随着多排孔列距动力机器基础距离的逐渐增大，多排孔列的平均隔振效果先逐步提高后逐步趋于稳定，总体上讲，对多排孔平均隔振效果影响不大。因此，在实际工程设计时，可结合地面振动的衰减规律和实际工程条件确定多排孔列的位置。

5 结" 论

针对动力机器基础振动影响的多排孔列近场主动隔振问题，采用饱和土三维半解析BEM建立了多排孔列近场隔振的边界元方程，提出了饱和土半解析BEM的SPMD并行算法并编程实现；同时，利用孔列在空间上的对应关系构建了一种边界元影响系数矩阵生成的优化算法；基于此，对多排孔列近场主动隔振问题进行了深入探讨，主要结论如下：

（1）对于多排孔列隔振问题，采用饱和土半解析BEM的SPMD并行算法结合边界元影响系数矩阵生成的优化算法可大大减少计算耗时，影响系数矩阵的生成时间约为并行算法耗时的4/N（N为多排孔总孔数）左右，计算效率得到显著提升。

（2）在饱和地基中设置多排孔列能够有效降低屏障后的位移振幅；多排孔列的布孔方式对其隔振效果基本无影响。多排孔列几何尺寸对隔振效果有较大影响：增加每排孔的孔数、减小孔间净距、增大孔径均能有效提高隔振效果；孔列的深度为时隔振效果最佳；而多排孔列的排数和排间距对隔振效果影响相对较小。此外，随着多排孔列距动力机器基础距离的逐渐增大，多排孔的隔振效果先提高后逐步趋于稳定。在实际工程设计时，建议多排孔列排数宜取两排，采用交错布孔方式，排孔孔深取，孔径取0.15，孔间净距取0.1，排孔孔数宜根据所需屏蔽区域的面积进行合理确定。

（3）本文可为非连续屏障（孔列、桩列）隔振问题的计算分析提供一种高效算法；同时，本文研究成果可为多排孔列隔振系统的工程应用提供必要的理论指导。

参考文献：

［1］""""""" 杨先健. 工业环境振动中的土动力学问题［J］. 岩土工程学报， 1992， 14（2）： 82-88.

［2］""""""" WOODS R D， BARNET N E， SAGESSER R. A new tool for soil dynamics［J］. Journal of Geotechnical Engineering Division， ASCE， 1974， 100（11）： 1234-1247.

［3］""""""" LIAO S， SANGREY D A. Use of piles as isolation barriers［J］. Journal of Geotechnical Engineering Division， ASCE， 1978， 104（9）： 1139-1152.

［4］""""""" 丁松波， 吴从师， 罗杰峰， 等. 地铁基坑爆破中减振孔的降振效果实测研究［J］. 铁道科学与工程学报， 2014， 11（4）： 85-89.

DING Songbo， WU Congshi， LUO Jiefeng， et al. Study on the effect of damping hole on reducing blasting vibration under the excavation of subway foundation［J］. Journal of Railway Science and Engineering， 2014， 11（4）： 85-89.

［5］""""""" 徐平， 夏唐代， 周新民. 单排空心管桩屏障对平面SV波的隔离效果研究［J］. 岩土工程学报， 2007， 29 （1）： 131-136.

XU Ping， XIA Tangdai， ZHOU Xinmin. Study on effect of barrier of a row of hollow pipe piles on isolation of incident plane SV waves［J］. Chinese Journal of Geotechnical Engineering， 2007， 29 （1）： 131-136.

［6］""""""" 徐平. 多排弹性空心管桩屏障对平面SV波的隔离［J］. 岩土工程学报， 2011， 33（3）： 392-397.

XU Ping. Rows of elastic hollow pipe piles as isolation barriers for plane SV waves［J］. Chinese Journal of Geotechnical Engineering， 2011， 33（3）： 392-397.

［7］""""""" 徐平. 多排柱腔列对平面P波和SH波的隔离［J］. 工程力学， 2011， 28（5）： 78-83.

XU Ping. Isolation of plane P and SH waves by barriers composed of several rows of cylindrical cavities［J］. Engineering Mechanics， 2011， 28（5）： 78-83.

［8］""""""" TSAI P H， FENG Z Y， JEN T L. Three-dimensional analysis of the screening effectiveness of hollow pile barriers for foundation-induced vertical vibration［J］. Computers and Geotechnics， 2008， 35（3）： 489-499.

［9］""""""" 欧阳圳， 吴从师， 梁虎， 等. 爆破中隔振孔对Rayleigh波的隔振效果分析［J］. 工程爆破， 2017， 23（2）： 37-43.

OUYANG Zhen， WU Congshi， LIANG Hu， et al. Vibration isolation effect of the damping hole on the Rayleigh wave during blasting［J］. Engineering Blasting， 2017， 23（2）： 37-43.

［10］""""" 丁文湘， 丁海滨， 徐长节， 等. 强夯加固地基土振动传播特性及隔振孔隔振分析［J］. 噪音与振动控制， 2017， 37（4）： 121-125.

DING Wenxiang， DING Haibin， XU Changjie， et al. Analysis of vibration propagation characteristics and effect of vibration isolation holes in soil foundation reinforced by dynamic consolidation［J］. Noise and Vibration Control， 2017， 37（4）： 121-125.

［11］""""" 李校兵， 戴鹏燕. 饱和土中孔列对平面快纵波的隔离效应［J］. 地震工程与工程振动， 2011， 31（2）： 25-30.

LI Jiaobing， DAI Pengyan. Isolation effect of cavity array in saturated soils on plane fast longitudinal waves［J］. Journal of Earthquake Engineering and Engineering Vibration， 2011， 31（2）： 25-30.

［12］""""" 时刚， 李永辉. 饱和地基中多排孔远场被动隔振分析［J］. 振动与冲击， 2019， 38（1）： 29-36.

SHI Gang， LI Yonghui. Passive vibration isolation analysis for far field of multi-row holes in saturated soil［J］. Journal of Vibration and Shock， 2019， 38（1）： 29-36.

［13］""""" 孙连勇，时刚，崔新壮，等． 饱和地基中单排孔近场隔振的现场试验与数值分析［J］．山东大学学报（工学版） ， 2020， 50（3）： 88-97．

SUN Lianyong，SHI Gang， CUI Xinzhuang， et al．Field test and analysis of vibration isolation of machine foundation by a row of holes in saturated soil［J］．Journal of Shandong University （Engineering Science）， 2020， 50（3）： 88-97．

［14］""""" SCHANZ M， ANTES H， RUBERG T. Convolution quadrature boundary element method for quasi-static visco- and poroelastic continua［J］. Computers and Structures， 2005， 83（10）： 673-684.

［15］""""" G.D.马诺利斯， D.E.贝斯科思. 弹性动力的边界单元法［M］. 周锡礽，等，译.天津：天津科学技术出版社， 1991.

［16］""""" 时刚， 高广运. 饱和地基中单排桩远场被动隔振研究［J］. 振动工程学报， 2010， 23（5）： 546-553.

SHI Gang， GAO Guangyun. Three-dimensional analysis of a row of piles as passive barriers in saturated soil［J］. Journal of Vibration Engineering， 2010， 23（5）： 546-553.

［17］""""" SYMM G T. Boundary elements on a distributed array processor［J］. Engineering Analysis， 1984， 1（3）： 162-165.

［18］""""" DAVIES A J. Parallel implementations of the boundary element method［J］. Computers amp; Mathematics with Applications， 1996， 31（6）： 33-40.

［19］""""" 尹欣. 三维弹性问题边界元法并行计算及其工程应用［D］. 北京： 清华大学， 2000.

YIN Xin. Parallel computation of 3D elasitc problems with BEM and its engineering application［D］. Beijing： Tsinghua University， 2000.

［20］""""" 雷霆， 姚振汉， 王海涛. 快速多极与常规边界元法机群并 行计算的比较［J］. 工程力学， 2006， 23（11）： 28-32.

LEI Ting， YAO Zhenhan， WANG Haitao. The comparison of parallel computation between fast multipole and conventional BEM on PC cluster［J］. Engineering Mechanics， 2006， 23（11）： 28-32.

［21］""""" 张健飞， 姜弘道. 基于边界元法的弹性动力问题并行求解［J］. 应用力学学报， 2008， 25（4）： 572-577.

ZHANG Jianfei， JIANG Hongdao. Parallel algorithms to solve elasto-dynamic problem based on boundary element method［J］. Chinese Journal of Applied Mechanics， 2008， 25（4）： 572-577.

［22］""""" 张健飞， 姜弘道. 集群上的弹性静力问题并行边界元解法及其工程应用［J］. 应用基础与工程科学学报， 2011， 19（1）： 133-144.

ZHANG Jianfei， JIANG Hongdao. Parallel boundary element method for elasto-static problem on cluster and its application［J］. Journal of Basic Science and Engineering， 2011， 19（1）： 133-144.

［23］""""" 王英俊， 王启富， 王钢，等. CUDA架构下的三维弹性静力学边界元并行计算［J］. 计算机辅助设计与图形学学报， 2012， 24（1）： 112-119.

WANG Yingjun， WANG Qifu， WANG Gang， et al. CUDA based parallel computation of BEM for 3D elastostatics problem［J］. Journal of Computer-Aided Design amp; Computer Graphics， 2012， 24（1）： 112-119.

［24］""""" 张锐， 文立华， 校金友. 大规模声学边界元法的GPU并行计算［J］. 计算物理， 2015， 32（3）： 299-309.

ZHANG Rui， WEN Lihua， XIAO Jinyou. GPU- accelerated boundary element method for large-scale problems in acoustics［J］. Chinese Journal of Computational Physics， 2015， 32（3）： 299-309.

［25］""""" 时刚， 高广运， 冯世进. 饱和层状地基的薄层法基本解及其旁轴边界［J］. 岩土工程学报， 2010， 32（5）： 664-671.

SHI Gang， GAO Guangyun， FENG Shijin. Basic solution of saturated layered ground by thin layered method and its paraxial boundary［J］. Chinese Journal of Geotechnical Engineering， 2010， 32（5）： 664-671.

［26］""""" DOBLARÉ M， GRACIA L. On non-linear transformations for the integration of weakly-singular and Cauchy principal value integrals［J］. International Journal for Numerical Methods in Engineering， 1997， 40（18）： 3325-3358.

［27］""""" PACHECO P S. 并行程序设计导论［M］. 邓倩妮，等，译. 北京： 机械工业出版社， 2014.

［28］""""" 刘维. 实战Matlab之并行程序设计［M］. 北京： 北京航空航天大学出版社， 2012.

第一作者： 时" 刚（1978―），男，博士，教授。E-mail： shigang@zzu.edu.cn

通信作者： 张" 浩（1985―），男，博士，副教授。E-mail： tmzhanghao@zzu.edu.cn

基金项目："国家自然科学基金资助项目（52078469）