基于模糊模型预测控制的电池均衡研究

摘 要：为了提升锂离子电池组均衡系统的性能，提出了一种基于模糊自适应模型预测控制（fuzzy adaptive model predictive control，FAMPC）的模块化均衡系统。首先，由改进的buck-boost电路和反激变压器组成双层均衡拓扑结构；其次，以不同电池剩余容量（state of charge，SOC）的状态作为模糊逻辑算法的输入，对均衡电流的约束条件进行调节；再次，基于FAMPC均衡控制方法，直接利用开关管的占空比作为系统输入；最后，在改变电池组状态并不使用额外电流控制机制的情况下进行仿真实验。结果表明，与传统的模糊控制方法相比，所提系统在正常条件下均衡速度提高了约24.51%，在电池低SOC的极端条件下均衡速度可以进一步提高至34.48%。所提系统将模糊算法提供的稳定性与模型预测控制算法的快速性相结合，保证了电池组更安全稳定的运行，可为电池组性能提升研究提供参考。

关键词：储能技术；主动均衡；模型预测控制；模糊逻辑算法；自适应

中图分类号：TM912

文献标识码：A"" DOI：10.7535/hbkd.2025yx01003

收稿日期：2024-08-23；修回日期：2024-09-19；责任编辑：冯民

基金项目：

国家自然科学基金（52207233）

第一作者简介：

刘光军（1976—），男，湖北武汉人，讲师，博士，主要从事电力电子方面的研究。

E-mail：20161023@hbut.edu.cn

Research on battery balancing based on fuzzy

model predictive control

LIU Guangjun， WANG Yutao， MA Liyang， WU Tiezhou，TIAN Aina

（Key Laboratory of Efficient Utilization and Storage Operation Control of Solar Energy in Hubei Province，

Hubei University of Technology， Wuhan， Hubei 430068， China）

Abstract：To improve the performance of lithium-ion battery pack balancing system， a modular balancing system based on fuzzy adaptive model predictive control

（FAMPC） was proposed. Firstly， a dual-layer balancing topology structure was composed of an improved buck-boost circuit and a flyback transformer. Secondly， using the state of charge （SOC） at different levels of battery remaining capacities as inputs for the fuzzy logic algorithm， the constraints on the balancing current were adjusted. Then， based on FAMPC balancing control method， the duty cycle of the switching transistor was directly used as the system input. Finally， simulation experiments were conducted without employing additional current control mechanisms to change the battery pack state. The results show that compared with traditional fuzzy control methods， the proposed system increase the balancing speed by approximately 24.51% under normal conditions and can further increase the balancing speed to 34.48% under extreme conditions with low battery SOC. The proposed system combines the stability provided by fuzzy algorithms with the rapid response of model predictive control algorithms， ensuring safer and more stable operation of the battery pack， which can provide reference for the research of enhancing battery pack performance.

Keywords：energy storage technology; active balancing; model predictive control; fuzzy logic algorithm; self-adaption

在全球能源转型与生态环境保护的大背景下，锂离子电池已成为推动电动汽车和可再生能源存储系统技术革新的关键驱动力^[1]。然而，随着电池包规模日益扩大，不同电池之间容量和电压不平衡问题日益凸显，严重影响了整体电池系统的效能和安全性^[2-3]。因此电动汽车电池均衡系统的研究具有重要意义。

被动均衡的均衡结果以电池组最低能量单体为基准，能量损耗较为严重。所以，主动均衡成为当今电池管理系统中的研究热点。工作电压是现在均衡研究中使用较多的均衡变量^[4-6]，具有测量方便的优点。但是当电池的

电池剩余容量（state of charge，SOC）处于10%～90%时，不同的SOC对应的电压差较小，这对电压测量精度有较高的要求。并且在一些工况下有电池电压相同但SOC不同的情况，这会导致均衡系统不能准确动作。所以把SOC作为均衡变量时可以最大程度上实现串联电池组的准确均衡^[7-8]，并且被越来越多的均衡研究所采用。也有部分研究采用混合变量的方式进行电池均衡，当电池处于电压平台期时以SOC作为均衡变量，当电池处于指数期时以电压作为均衡变量^[9-11]。当前研究中使用较多的均衡拓扑包括基于电容、电感和变压器的均衡拓扑。基于电感的均衡拓扑可以灵活改变均衡电流，具有较强的可控性^[12-14]，是目前使用较多的均衡拓扑；基于变压器的均衡拓扑具有功率等级高和电气隔离的优点^[15-17]，适合在模块间均衡使用。控制方式的选择也是当今均衡系统研究的一个主要方向。恒流均衡模式以恒定的均衡电流为基础，选择合适的均衡路径^[18]；电流可变的均衡方式在确定均衡路径以后，根据当前状态选择合适的均衡电流实现电池组均衡^[19-21]。

本文基于已有的均衡系统研究，提出一种保证锂离子电池更安全和更稳定运行的模糊自适应模型预测控制（fuzzy adaptive model predictive control，FAMPC）模块化均衡系统。

1 电池组均衡拓扑结构及原理

1.1 电池组均衡结构

采用buck-boost电路与反激变换器相结合的方式，建立模块化均衡拓扑结构，提升电池组均衡速度，其原理如图1所示。该均衡拓扑可以以模块为单位对均衡系统进行拓展，具有较强的实用性。本文所研究验证的均衡电路将8节电池分为2个模块，其中每个模块包含4节电池。在此基础上，以模块为单位，分别对每个均衡电路进行基于模型预测控制的电池均衡控制。与直接对8节电池进行控制相比，分模块控制可大大减少模型预测控制中相关系数矩阵的阶数，进而减小计算量，提升计算速度。

1.2 模块内均衡原理

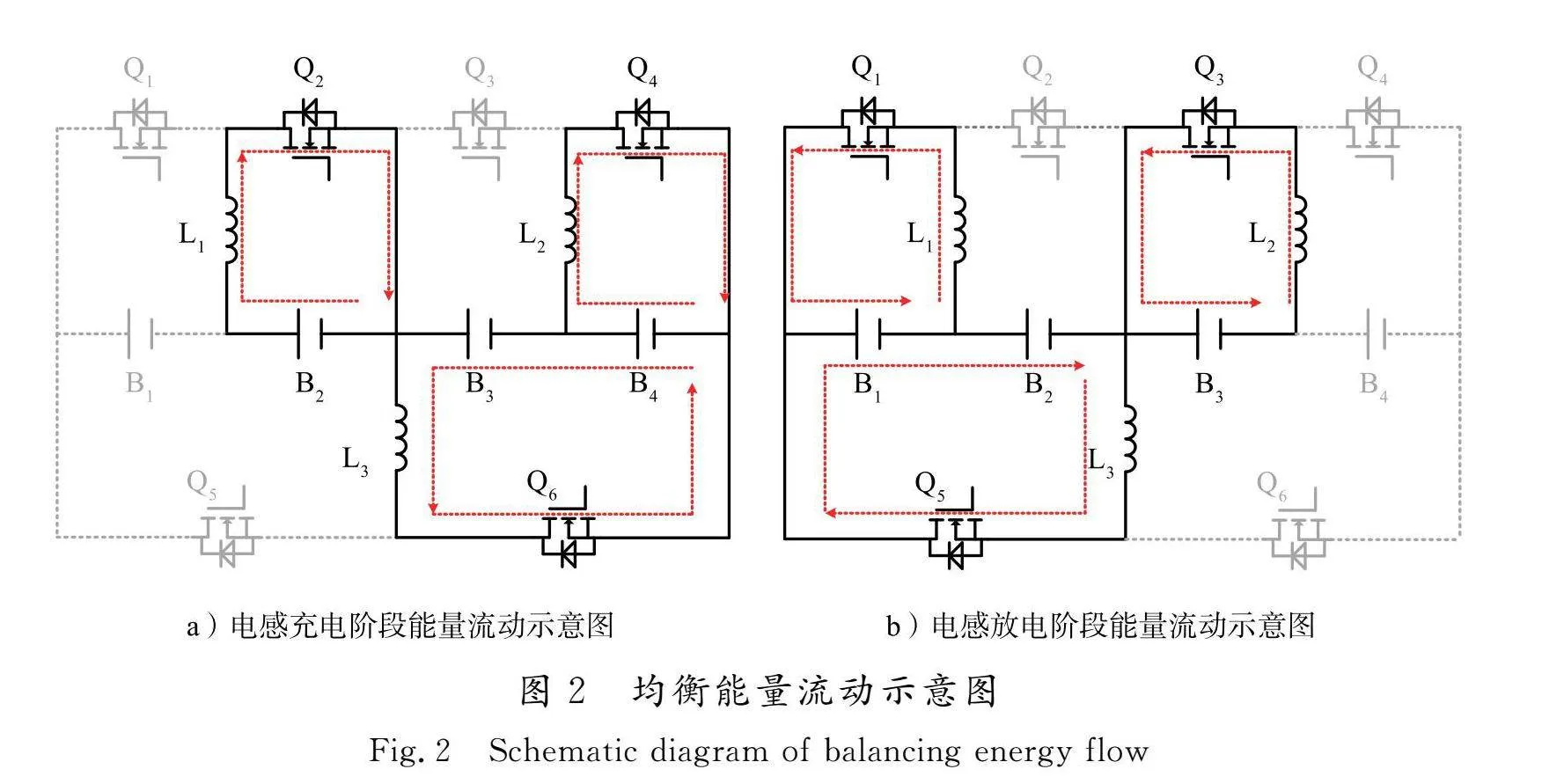
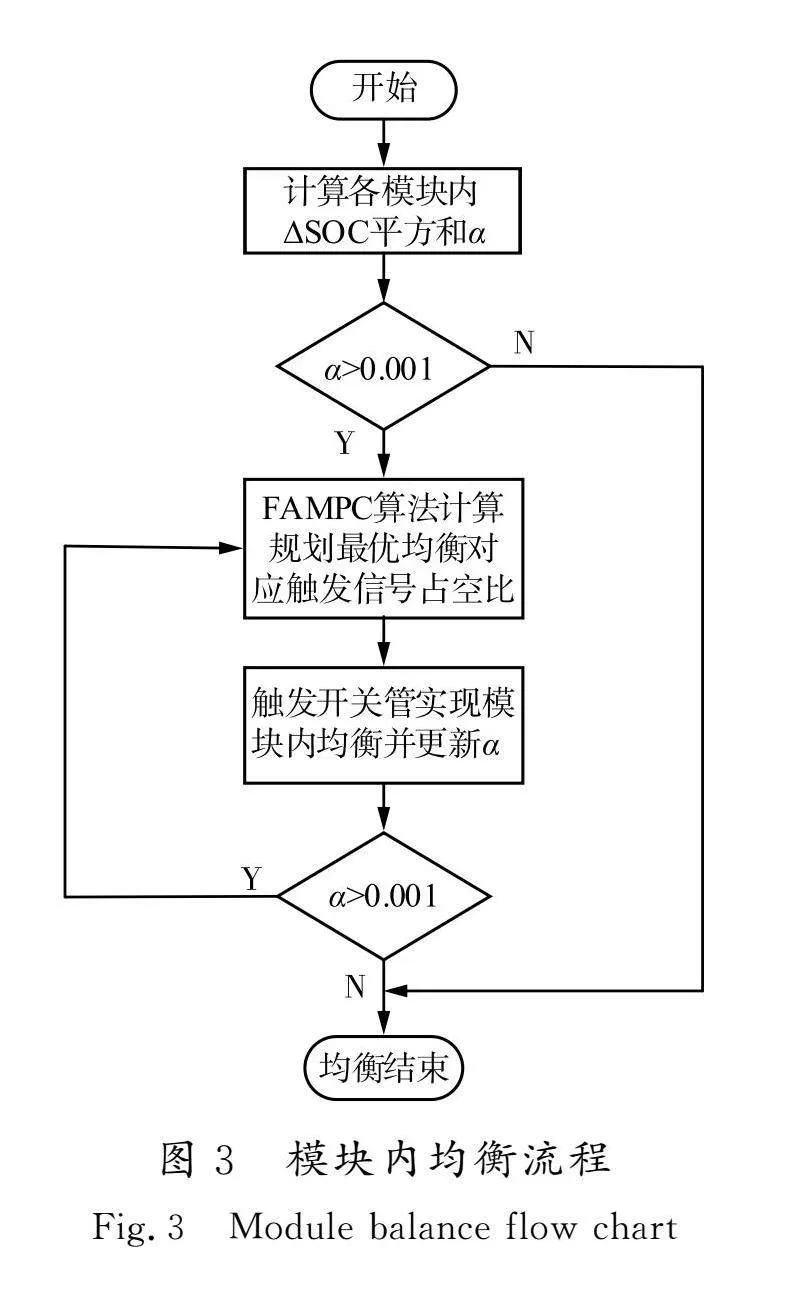
传统的buck-boost均衡电路中，相邻两节电池之间所连接的电感作为能量传递的介质。当电池SOC差存在于首尾电池之间时，电池能量传递路径较长。而在本文所采用的均衡拓扑中，以电池B4的SOC大于B1为例，其中一种能量流动方式如图2所示。假设均衡电流平均值均相等，那么一个周期结束时，电池B2和B3的SOC不改变，可以看作是电池B4直接给B1充电。因此，相较于传统的buck-boost均衡电路拓扑，该模块内均衡电路可以减少电池均衡路径和均衡时间。但这只是能量传输方式的一种，具体均衡过程中控制算法会结合实际工况在众多传输方式中选出最优的一种，其流程如图3所示。其中ΔSOC表示模块内单体电池SOC与模块内平均SOC的差值。

假设电池B1 SOC大于B 首先给开关管Q1触发脉冲使其导通，此时，电池B1给电感L1充电。

流经电感L1的电流I1-2与电池B1两端电压VB1之间的关系如式（1）所示。

I1-2=VB1L1t，" 0lt;tlt;DT ，（1）

式中：T为触发脉冲的周期；D为触发脉冲的占空比。

t=DT时刻，关闭开关管Q1。此时电感L1的电感电流与电池B2端电压VB2关系如式（2）所示。

I1-2=VB1L1DT-VB2L1（t-DT）， DTlt;tlt;T。（2）

由式（1）、式（2）可知，当t=DT时，电感中电流达到峰值，为VB1L1DT。为了保证电感拥有更好的运行特性，本文将电感运行状态限制在断续范围内。

1.3 模块间均衡原理

模块间采用多耦合变压器组成的反激变换器作为电池能量传递的桥梁，所对应的原理如图1 b）所示。以模块1和模块2为例，对模块间的均衡原理进行分析。反激变换器仍然运行在断续模式，且由于每组内电池的数量相等，线圈的匝数比也都设置为1。

首先触发导通开关管S 此时施加在变压器原边线圈的电池组电压为V 电压电流关系如式（3）所示，其中L为反激变换器励磁电感的电感值。

I1=V1Lt， 0lt;tlt;DT 。（3）

当S1关断以后，线圈内储存的磁能在副边侧以电流的方式通过开关管S2释放出来，实现对模块2的充电。其电压电流关系如式（4）所示，其中V2为模块2端电压，且t=T*时，电流为0。

I2=V1LDT-V2L（t-DT）， DTlt;tlt;T* 。（4）

2 模糊逻辑控制

锂离子电池的端电压并非完全是一个常数，它会因SOC的不同而发生相对应的改变。采用模糊逻辑算法综合考虑电池的电压特性曲线和不一致性对均衡电流进行约束，有利于提高均衡系统的稳定性。

2.1 电池电压影响

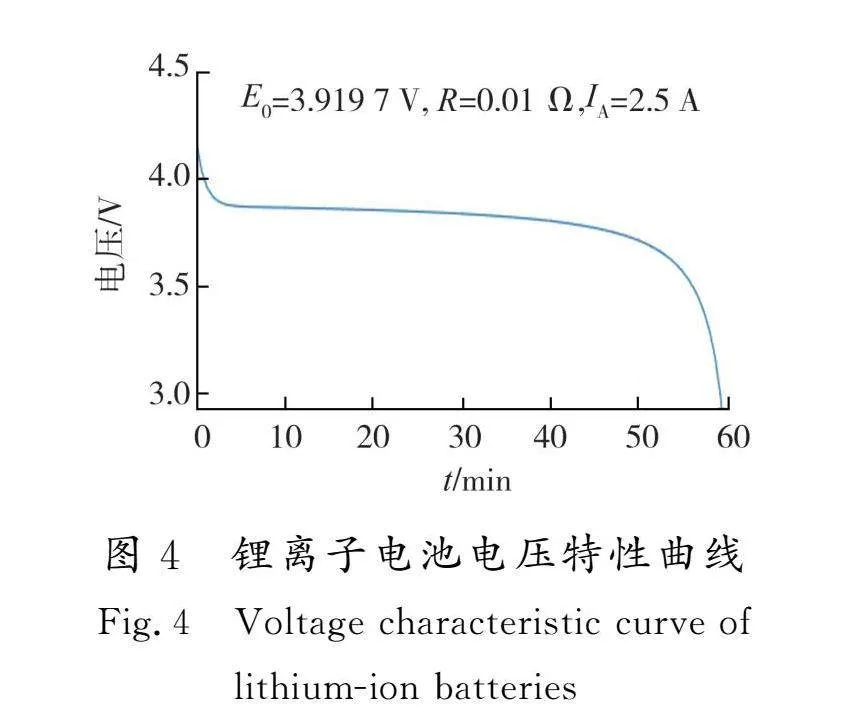
本文仿真所用电池模型参数以圆柱型FCB21700L4R2C2500锂离子电池的参数为基准，具体数值如表1所示，其对应的额定放电曲线如图4所示。其中E0代表电压进入平台期时电池端电压，R代表电池直流内阻，IA代表电池的额定放电电流。

可以看出，当电池的SOC值较低时，电池的端电压随SOC变化的比率较高，此时应该尽可能快地进行电池均衡，以减少电池间的不一致性对整个电池组运行的不良影响。当电池的SOC值适中时，电池进入电压平台期，SOC的差异对于电压的影响较小。电池SOC值较大时，意味着整个电池组所储存的能量较高，安全稳定运行条件则显得更加重要。这种条件下，可以适当减小均衡电流来提升整个电池组的稳定性。

2.2 隶属度函数设计

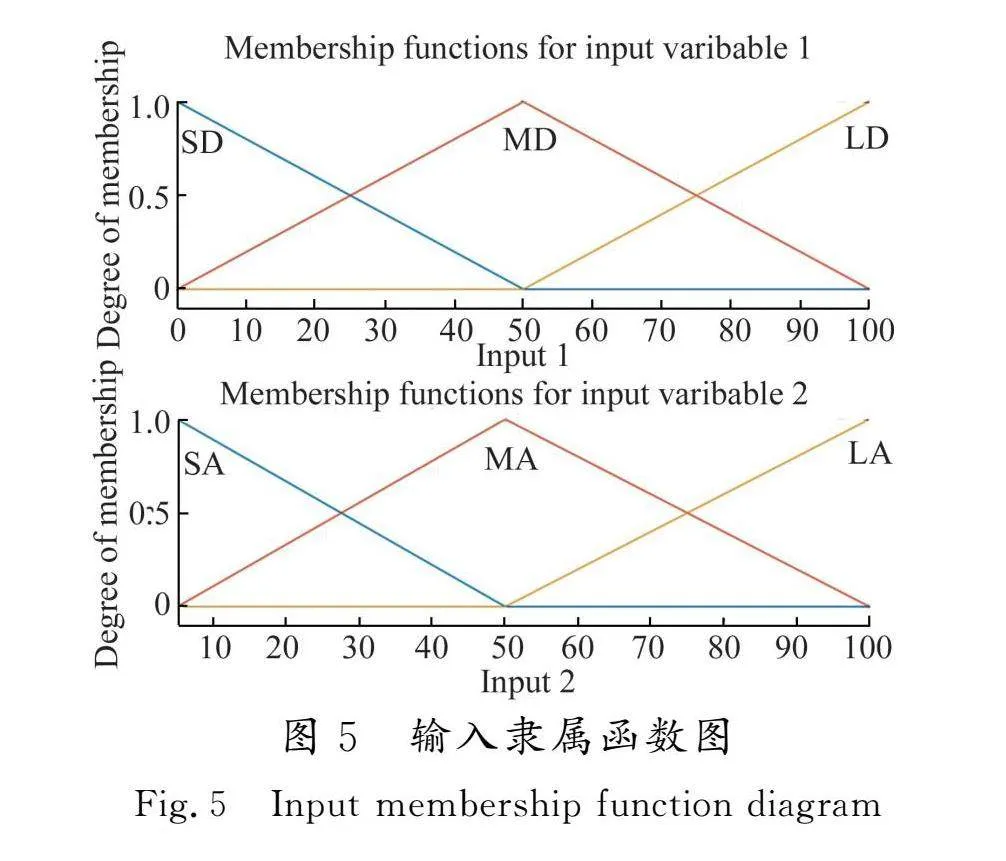
本文所提的模糊算法中，以电池组中最大SOC差值的2倍SOCd和电池平均SOC值SOCav作为输入条件，以参考输入电流

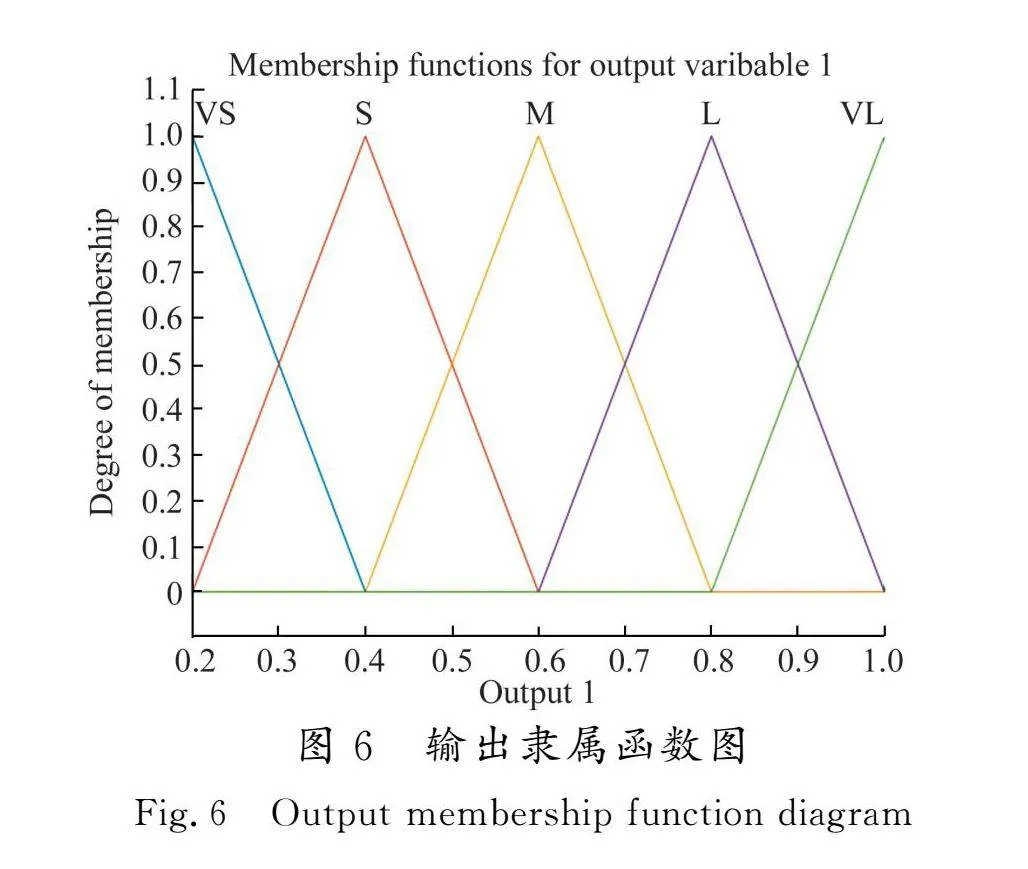
Iref的倍数kref为输出。当SOCd取值超过100时一律按照100的极端条件来计算。其中SOCd和SOCav的模糊论域都为[0，100]，输出系数kref的模糊论域为[0. 1]。2个输入均采用3个模糊变量，分别对应为[s，m，l]。SOCd的取值区间对应为[0，0，50]，[0，50，100]和[50，100，100]，SOCav的取值区间对应为[" 50]，[ 50，100]和[50，100，100]。输出采用5个模糊变量，[VS，S，M，L，VL]对应的取值区间分别为[0. 0. 0.4]，[0. 0. 0.6]，[0. 0.6，0.8]，[0.6，0.8，1]和[0.8， 1]。本设计中采用三角隶属度函数，所对应的图像如图5、图6所示。

2.3 模糊规则设计

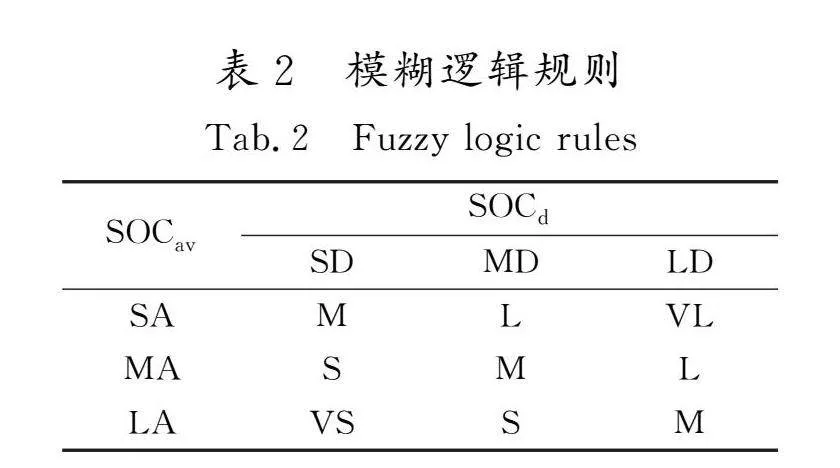
当电池SOC差异较大时，电池组特性受其影响较大，应尽可能快地减少电池之间的SOC差异；随着均衡进程的进行，SOC差异逐渐减小，均衡电流的大小也可适当进行缩减。结合前文指出的电池组平均SOC对应的均衡电流约束，可以得出整个模糊算法的模糊规则如表2所示。

2.4 去模糊化

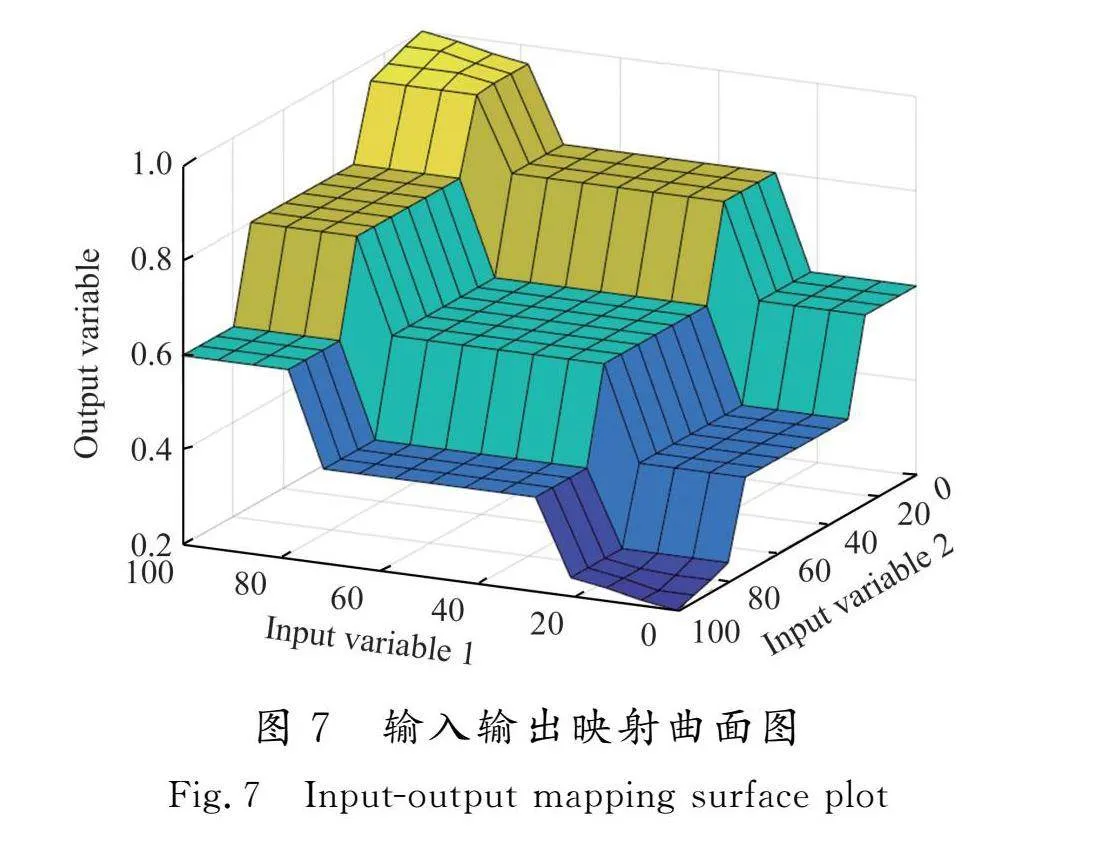
本文模糊算法采取的去模糊化方式为平均最大隶属度法，不同输入条件对应的输出映射曲面图见图7。

3 模糊自适应模型预测控制

3.1 模型预测控制模型建立

基于模型预测控制的原理，对前文所提模块内均衡电路拓扑进行数学建模。每个均衡模块内包含4个串联单体电池，因此以每节电池的SOC和模块内4节电池的平均SOC之差作为状态变量，则该均衡系统的状态向量为

xk=［ΔSOC ΔSOC ΔSOC ΔSOC4］ 。（5）

以每个均衡电路中相对应的开关管占空比作为模型预测控制系统的输入量。当2节电池之间有能量传输时，以输入量的正负表示能量传递的方向。电池1向电池2充电，电池3向电池4充电，电池12向电池34充电取值为正，相反方向则取值为负。则输入向量为

uk=［D D D3］ 。（6）

均衡系统运行的理想目标是所有电池的SOC相等，即系统的状态向量和输出向量均为零向量，所以本系统输出的参考值为零，进而可以得出系统的误差ek。

ek=xk 。（7）

综上所述，模块内模型预测控制均衡系统的状态空间模型可以表示为

xk+1=Axk+Buk ，（8）

式中：B为状态转移矩阵，矩阵内元素构成与电路拓扑及采样时间有关；A为4阶单位矩阵。如果直接对8节电池采用模型预测控制，系数矩阵将为8阶。故模块化均衡大大降低了状态转移矩阵的复杂程度，进而可显著减少均衡系统的计算量。

以二次规划为基础构造控制系统的代价函数，可得到该系统的代价函数为

J=∑N-1i=0（x（k+i|k）T

Qx（k+i|k）+u（k+i|k）TRu（k+i∣k））+

x（k+N）TFx（k+N） ，（9）

式中：Q为误差加权和系数矩阵；R为输入加权和系数矩阵；F为终端误差系数矩阵。矩阵Q和R均为对角矩阵。

系统初始状态为xk=x（k|k），进而对预测区间N内的系统状态进行预测，得到

x（k|k）=xk，

x（k+1|k）=Amx（k|k）+Bmu（k|k），

x（k+2|k）=A2mx（k|k）+AmBmu（k|k）+Bmu（k+1|k），

x（k+N|k）=ANmx（k|k）+A^N-1mBmu（k|k）+…+Bmu（k+N-1|k）。（10）

用矩阵形式表示为

Xk=Mxk+CmUk ，（11）

Xk=［x（k|k）， x（k+1|k），…，x（k+N|k）］，（12）

Uk=［u（k|k）， u（k+1|k），…，u（k+N-1|k）］，（13）

M=IAmA2m

ANm;

Cm=0…0

Bm

0

A^N-1mB…Bm 。（14）

其中令=diag［Q，Q，…，F］，=diag［R，R，…，R］，则代价函数可以表示为

J=XTkXk+UTkUk 。（15）

通过合理的系数设置，计算得出代价函数取最小值所对应的输入向量，该结果就是系统的最优控制输入向量。

3.2 模糊自适应约束

虽然可以通过改变代价函数中相关的系数矩阵来改变SOCd和均衡电流所占的权重，但是二者之间没有一个明确的相关性关系，且无法体现不同SOCav对均衡系统参数的要求。在模型预测控制中引入第2节所提模糊逻辑算法，根据不同的电池状态对模型预测控制的输入约束进行调整，可以在保证系统稳定性的基础上提高系统的均衡速度。则系统的最大输入电流应为

Imax=krefIref 。（16）

由图4锂电池两端电压随电池SOC变化的曲线可知，当SOC较小时，锂电池输出电压明显小于其额定电压。前文所建立的均衡电路模型中，认为电池两端的电压恒为额定输出电压。在这种情况下，相同的占空比所产生的均衡电流小于理想值，均衡速度会在一定程度上变慢。而当某电池单体的电量消耗完时，串联电池组会因端电压无法满足需求而停止运行。因此为了更加充分地运用电池组的电量，应在电池SOC较低时，对模型的状态转移矩阵进行自适应调整来增加系统的准确性。

在每次进行模型预测控制算法的计算时，对比当前时刻各电池的SOC值，寻找出每个均衡电路中SOC较高的部分，用该部分的电池电压与标准电压的比值k来自适应调整状态转移矩阵系数。

Breal=kB 。（17）

当电池组平均SOC处于5%～15%区间时，应该加快对能量较低电池的充电速度，对系统模型的输入约束条件也可以进一步进行自适应调整，把电池的充电电流约束条件改为原来约束值的1/k。

Imax，real=Imax/k 。（18）

所以，模糊自适应模型预测控制的提出，不仅将模糊逻辑算法提供的稳定性和模型预测控制算法提供的快速性相结合，而且使开关管占空比直接作为控制系统输入成为可能。即使没有特定的电流控制环节，该控制策略仍然能在不同电池组状态下稳定运行。

4 结果分析

为了验证本文所设计电池均衡系统的有效性，使用MATLAB的simulink模块构建了以8节电池组成的2层均衡电路模型进行仿真实验，其中电池模型参数设计对应表1所列参数。为了便于器件选型，单体电池之间电感选择为0.5 mH。由表中提供的电池参数可知，电池的标准放电电流为2.5 A，则当开关频率为500 Hz时，既可以满足要求，也便于计算分析。为了满足同一占空比对应同一均衡电流，则双电池间电感和变压器励磁电感分别取1 mH和2 mH。

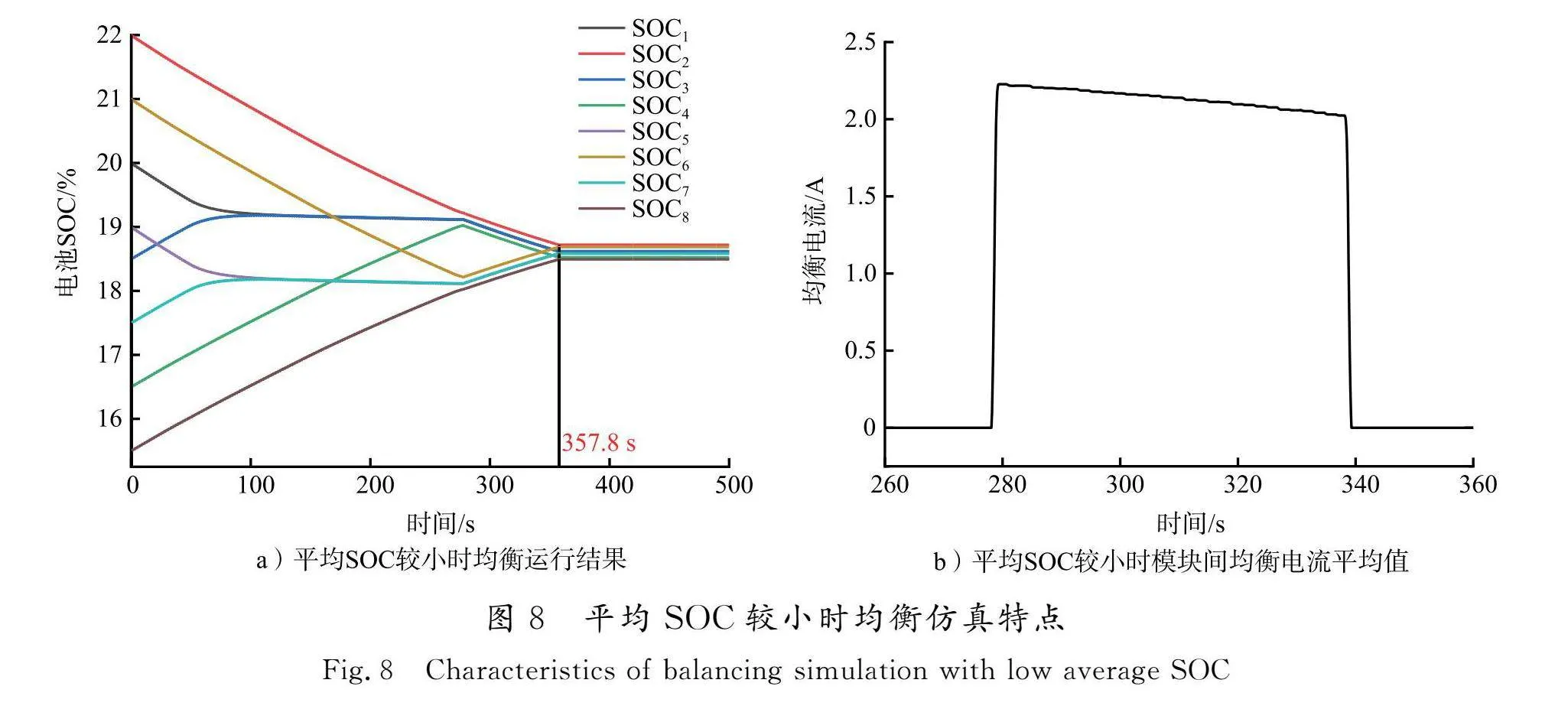
为了展示模糊逻辑控制器对于均衡电流的约束效果，对比不同均衡运行条件下的模块间均衡电流，结果如图8所示。可以看出，当2个模块之间SOC差异较大时，均衡系统应该尽可能快地实现电池模块间的均衡，减少电池之间的不一致性。而随着均衡进程的推进，电池组之间的SOC差异逐渐减小，电池之间的不一致性对于电池组的正常运行的影响也逐渐减小，

对于均衡速度的要求也逐渐降低，因此均衡电流的大小也应随着均衡进程的推进而减小。

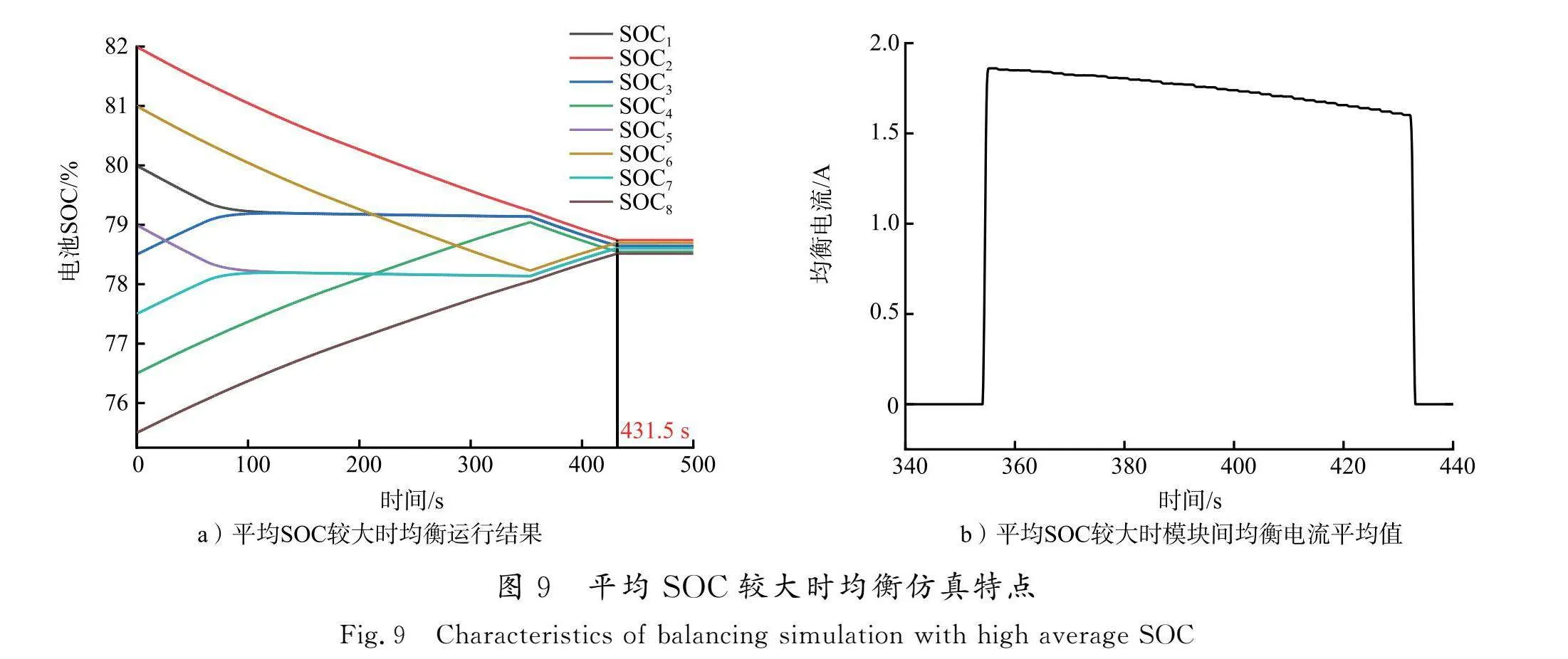
前文对于模糊规则的设计中提出，当电池的SOCav较大时，适当减小均衡电流的大小可以在一定程度上提升均衡系统运行过程中的稳定性。把每节电池的SOC值都提升60%，在其他条件都不变的基础上运行均衡系统，结果如图9所示。从电流平均值的波形图中可以看出，均衡系统运行时组间电流值出现了一定程度的减小，满足设计要求。

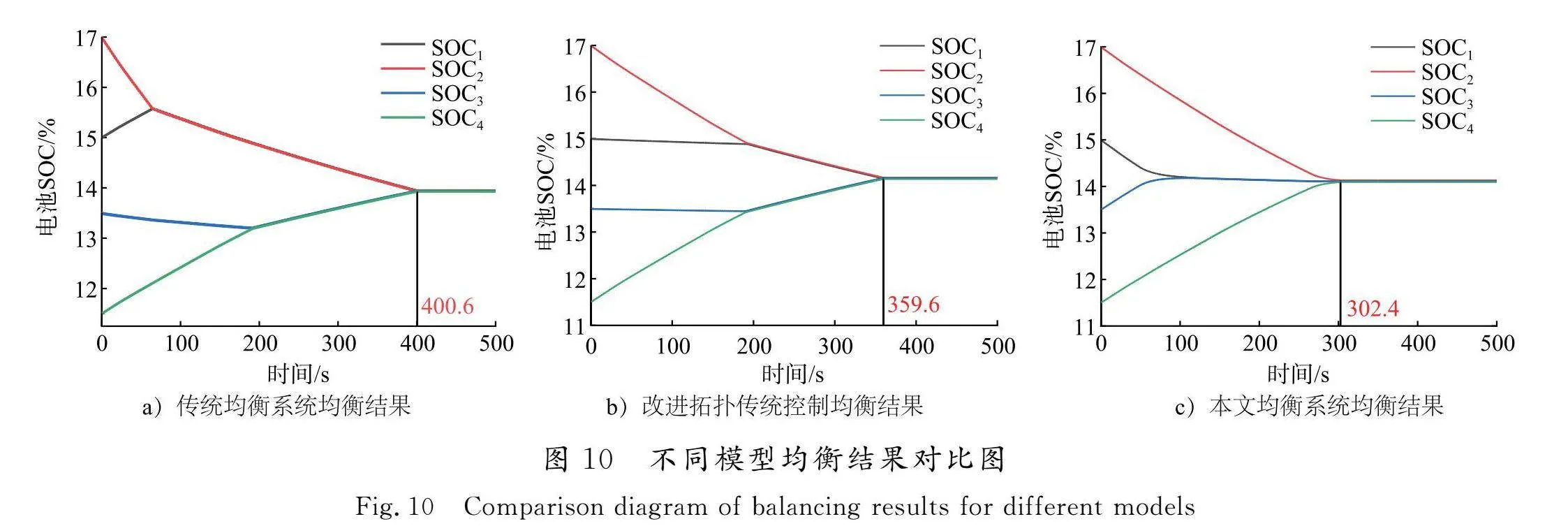
为了更加明显地展示不同均衡控制方式的特点，单独对模块内均衡进行仿真实验，结果如图10所示。从图10 a）和b）对比中可以得知，本文所提的均衡电路与传统的均衡电路相比，均衡完成时间从400.6 s减少到359.6 s，均衡速度提升约为10.23%。

在新拓扑电路的基础上，采用FAMPC控制方法，系统会在均衡电流重叠部分合理分配均衡电流来实现均衡过程的优化，结果如图10 c）所示。从均衡结果对比可以看出，当新的均衡拓扑与本文提出的控制方式相结合时，均衡时间能进一步被缩减为302.4 s，与传统拓扑和模糊逻辑控制方式相比较，均衡时间缩短约为24.51%。

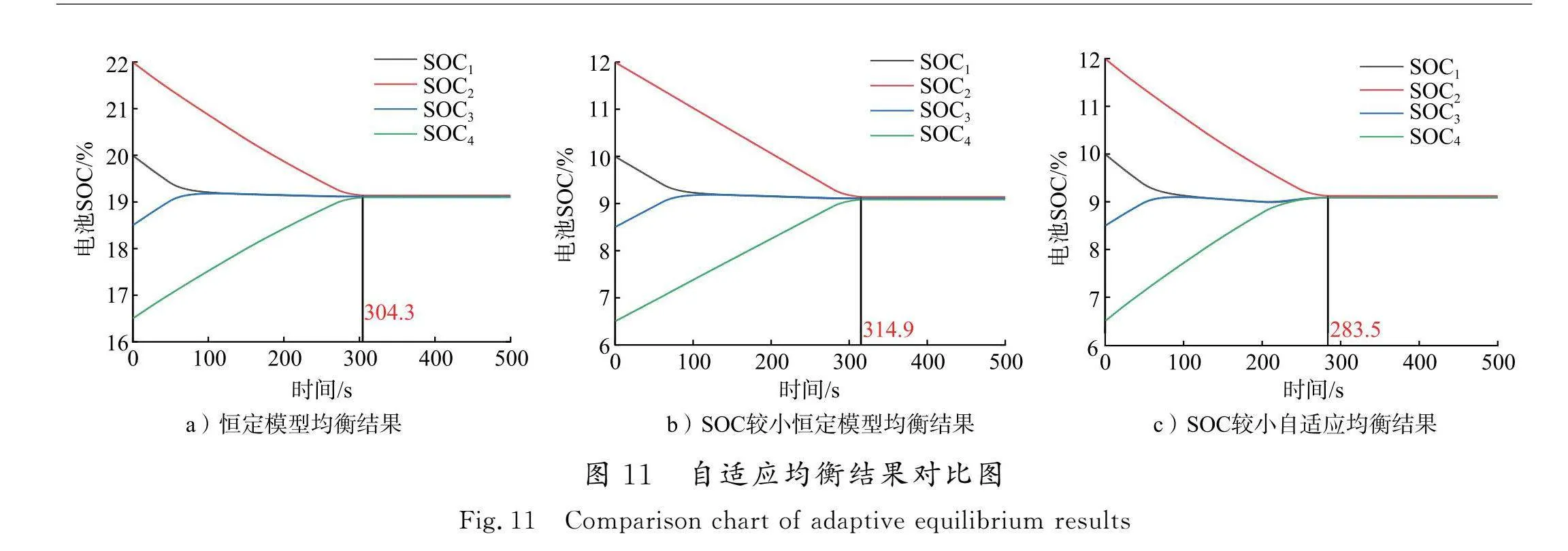
进一步调整电池组各单体电池的状态，分析本文所提控制方式的优势，结果如图11所示。从图11 a）和b）对比中可以看出，本文提出的以开关管占空比为控制对象的模型预测控制即使在电池输出电压随SOC降低出现明显改变的情况下仍然具有较强的可行性。

但是受到电池端电压降低的影响，相同占空比对应的均衡电流有较为明显的减小，因此恒定模型预测控制的均衡时间从304.3 s增加到314.9 s。为了解决这个问题，加入模型的自适应调整，从图11 b）和c）的对比中可以看出，新的均衡系统均衡速度进一步提高，均衡时间减少为283.5 s，均衡速度提升约9.97%。所以模糊自适应模型预测控制方法可以在电池SOC较低的极端情况下表现出更快的均衡速度，避免电池过度放电现象的出现。

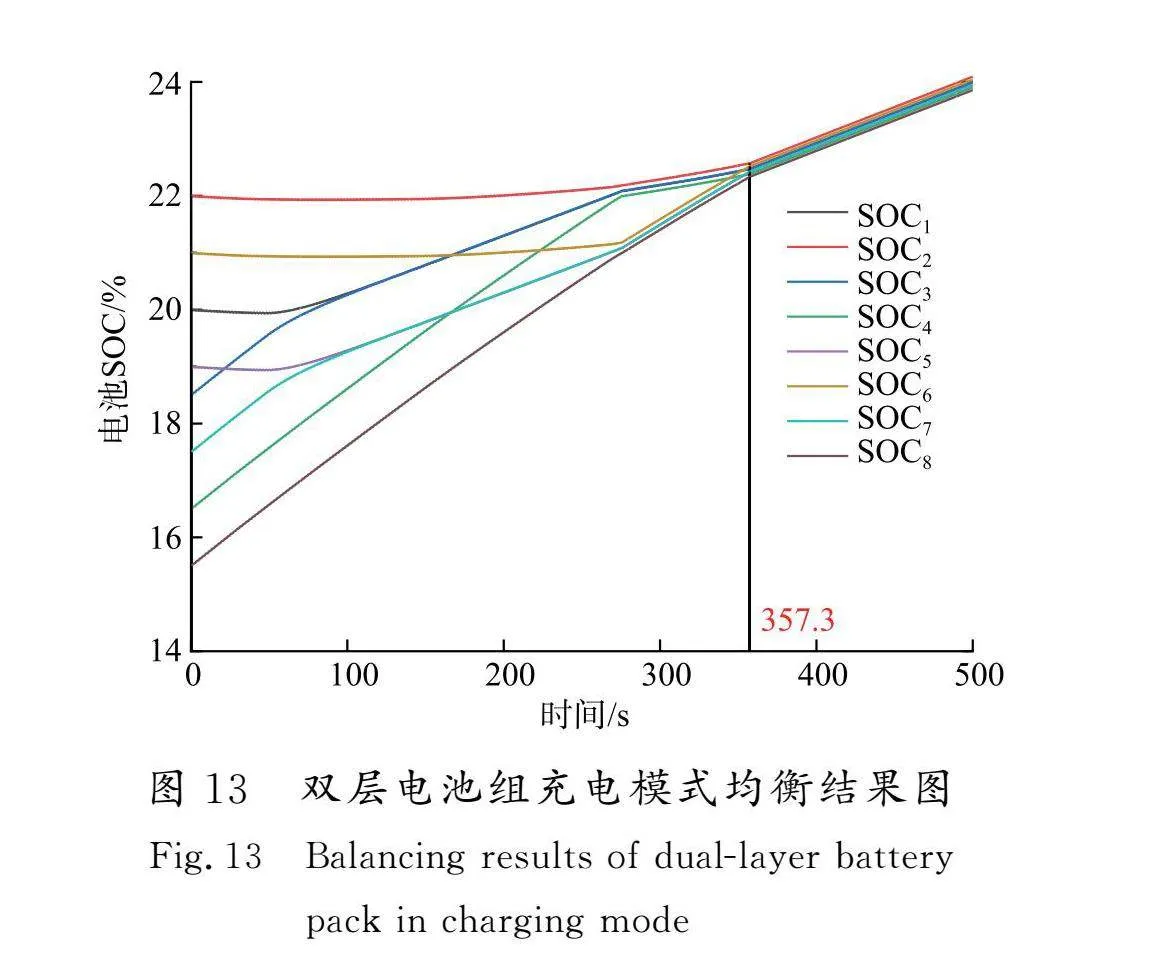
图12和图13所示为由2个模块组成的8节电池均衡系统分别在电池放电和充电2种运行模式下进行仿真验证的结果。首先2模块分别进行模块内的单体电池均衡，均衡效果和前文中单独进行模块内仿真的结果一致。当2模块内的均衡进程都结束后，模块间均衡系统得到启动信号，开始进行模块间均衡。从结果可以看出，无论是何种运行条件，本文所提出的均衡系统都能较为快速稳定地实现串联电池组的SOC均衡。

5 结 语

以buck-boost电路和反激变换器为基础，设计了一种模块化均衡拓扑结构，并基于不同运行条件下电池组的特性，提出考虑电池SOC差异和平均SOC的模糊逻辑算法来约束均衡电流；将模糊逻辑算法和自适应模型预测控制相结合，提出FAMPC控制策略，并搭建仿真模型，实现了串联电池组的主动均衡仿真。主要结论如下。

1）采用改进后的buck-boost电路为基础设计模块内均衡电路，可以在一定程度上减少首尾电池之间的均衡路径并提高控制灵活性，且采用模块化模型预测控制可以有效减少系统计算量。

2）传统的电池均衡系统要搭配电流控制电路使用，而本文提出的自适应模型预测控制方法直接将开关管的占空比作为系统的输入。在没有额外电流控制环节的情况下系统能依据其自身具有的反馈特性和自适应性实现整个均衡系统的稳定运行。

3）针对锂电池在不同SOC值时所表现的不同特性，均衡系统采用模糊逻辑算法进行约束值计算，可以在大电流快速均衡和低电流稳定均衡上做出合理的权衡，并且结合模型预测控制提供的快速性，使得均衡控制系统能既稳定又快速地实现锂离子电池组的SOC均衡。

所提均衡控制系统将模糊算法提供的稳定性与模型预测控制算法的快速性相结合，保证电池组更安全稳定的运行，因此在以锂电池作为能源储备的领域具有一定的参考价值。在后续的研究中，将尽快完成实验平台的搭建和调试，进一步进行相关的实验验证。

参考文献/References：

[1]

CHANG Chun，CHEN Lang，LIU Xiaoyu，et al.Electrochemical aging model of lithium-ion battery with impedance output and its parameter sensitivity analysis and identification[J].Journal of Energy Storage，2024.DOI： 10.1016/j.est.2024.111277.

[2] TIMILSINA L，BADR P R，HOANG P H，et al.Battery degradation in electric and hybrid electric vehicles：A survey study[J].IEEE Access，202 11：42431-42462.

[3] GENG Zeyang，THIRINGER T，LACEY M J.Intermittent current interruption method for commercial lithium-ion batteries aging characterization[J].IEEE Transactions on Transportation Electrification，202 8（2）：2985-2995.

[4] 杨晓光，赵小兵，聂宝鑫，等.集成均衡和保护功能的电池充放电电路[J].电源技术，202 47（12）：1655-1659.

YANG Xiaoguang，ZHAO Xiaobing，NIE Baoxin，et al.Battery charging and discharging circuit with integrated equalization and protection functions[J].Chinese Journal of Power Sources，202 47（12）：1655-1659.

[5] 刘自南，王斌，吴铁洲.锂离子电池均衡控制策略[J].实验室研究与探索，202 42（8）：5-9.

LIU Zinan，WANG Bin，WU Tiezhou.Lithium-ion battery balance control strategy[J].Research and Exploration in Laboratory，202 42（8）：5-9.

[6] 廖武兵.面向储能系统的新型电压均衡拓扑研究与开发[D].广州：华南理工大学，2022.

LIAO Wubing.Research and Development of Novel Voltage Equalization Topologies for Energy Storage Systems[D].Guangzhou：South China University of Technology，2022.

[7] 陈爱琢，张从佳，周杨林，等.基于动态可重构电池网络状态空间模型的电池荷电状态估计[J/OL].中国电机工程学报.（2024-05-20）[2024-08-28].https：//link.cnki.net/doi/10.13334/j.0258-8013.pcsee.232151.

CHEN Aizhuo，ZHANG Congjia，ZHOU Yanglin，et al.Battery state of charge estimation based on the dynamic reconfigurable battery network state space model[J/OL].Proceedings of the CSEE.（2024-05-20）[2024-08-28].https：//link.cnki.net/doi/10.13334/j.0258-8013.pcsee.232151.

[8] 卢志刚，苗泽裕，蔡瑶.考虑时变线阻的多储能SOC稳定均衡控制策略[J].高电压技术，202 50（1）：127-137.

LU Zhigang，MIAO Zeyu，CAI Yao.Stable equilibrium control strategy for multi-energy storage SOC considering time-varying linear resistance[J].High Voltage Engineering，202 50（1）：127-137.

[9] WU Tiezhou，JI Feng，LIAO Li，et al.Voltage-SOC balancing control scheme for series-connected lithium-ion battery packs[J].Journal of Energy Storage，2019.DOI： 10.1016/j.est.2019.100895.

[10]LI Penghua，LIU Jianfei，DENG Zhongwei，et al.Increasing energy utilization of battery energy storage via active multivariable fusion-driven balancing[J].Energy，2022.DOI： 10.1016/j.energy.2021.122772.

[11]HANNAN M A，HOQUE M M，PENG S E，et al.Lithium-Ion battery charge equalization algorithm for electric vehicle applications[J].IEEE Transactions on Industry Applications，2017，53（3）：2541-2549.

[12]姚芳，王晓鹏，陈盛华，等.基于Buck-Boost准谐振电路的电池自适应分组均衡方案研究[J].中国电机工程学报，202 43（2）：714-726.

YAO Fang，WANG Xiaopeng，CHEN Shenghua，et al.Research on battery adaptive grouping equalization scheme based on Buck-Boost quasi-resonant circuit[J].Proceedings of the CSEE，202 43（2）：714-726.

[13]刘征宇，许亚娟，余超，等.基于Buck-Boost电路的分层均衡方案[J].仪器仪表学报，2018，39（11）：87-94.

LIU Zhengyu，XU Yajuan，YU Chao，et al.Hierarchical equalization scheme based on Buck-Boost circuit[J].Chinese Journal of Scientific Instrument，2018，39（11）：87-94.

[14]刘征宇，孙庆，马亚东，等.基于Buck-Boost电路的能量转移型均衡方案[J].电机与控制学报，2017，21（9）：73-79.

LIU Zhengyu，SUN Qing，MA Yadong，et al.Energy-transferring equalization scheme based on Boost-Buck circuit[J].Electric Machines and Control，2017，21（9）：73-79.

[15]赵炎锋，王斌，杜睿，等.锂电池双向均衡及模型预测控制优化[J].西安交通大学学报，202 58（10）：24-35.

ZHAO Yanfeng，WANG Bin，DU Rui，et al. Bidirectional balancing and model predictive control optimization for lithium batteries[J].Journal of Xi'an Jiaotong University，202 58（10）：24-35.

[16]郑征，王肖帅，李斌，等.基于三绕组变压器的电池组新型均衡拓扑[J].太阳能学报，202 44（9）：518-526.

ZHENG Zheng，WANG Xiaoshuai，LI Bin，et al.New equalization topology for battery packs based on three-winding transformer[J].Acta Energiae Solaris Sinica，202 44（9）：518-526.

[17]QIN Dongchen，QIN Shuai，WANG Tingting，et al.Balanced control system based on bidirectional flyback DC converter[J].Energies，2022.DOI： 10.3390/en15197226.

[18]DING Xiaofeng，ZHANG Donghuai，CHENG Jiawei，et al.A novel active equalization topology for Series-Connected lithium-ion battery packs[J].IEEE Transactions on Industry Applications，2020，56（6）：6892-6903.

[19]ZHENG Jian，CHEN Jian，OUYANG Quan.Variable universe fuzzy control for battery equalization[J].Journal of Systems Science and Complexity，2018，31：325-342.

[20]WU Tezhou，QI Yibo，LIAO Li，et al.Research on equalization strategy of lithium-ion batteries based on fuzzy logic control[J].Journal of Energy Storage，2021.DOI： 10.1016/j.est.2021.102722.

[21]吴文进，郭海婷，苏建徽，等.基于自适应模糊PID算法的锂电池组双层均衡控制[J].电力系统保护与控制，202 52（2）：111-117.

WU Wenjin，GUO Haiting，SU Jianhui，et al.Dual-layer equalization control of Lithium batteries based on an adaptive fuzzy PID algorithm[J].Power System Protection and Control，202 52（2）：111-117.