基于CEEMDAN⁃TCN的短期风电功率预测研究

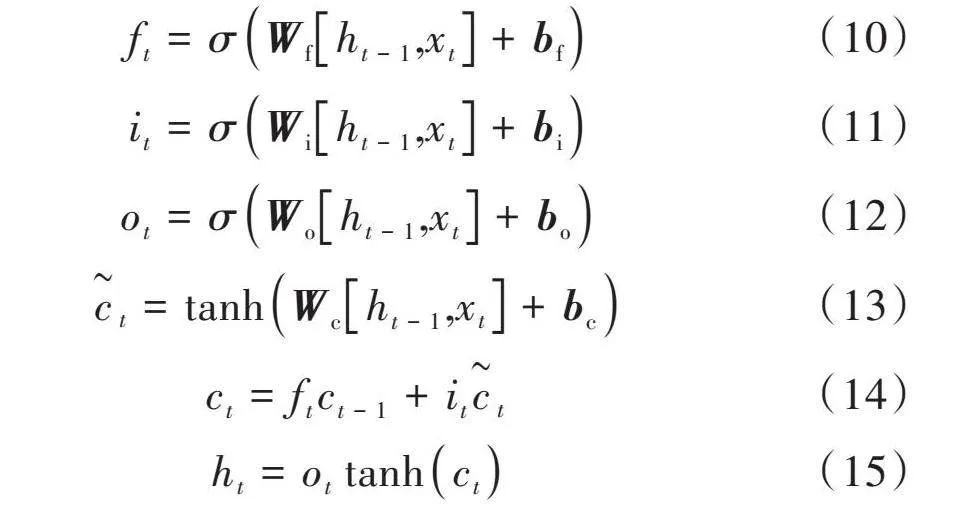
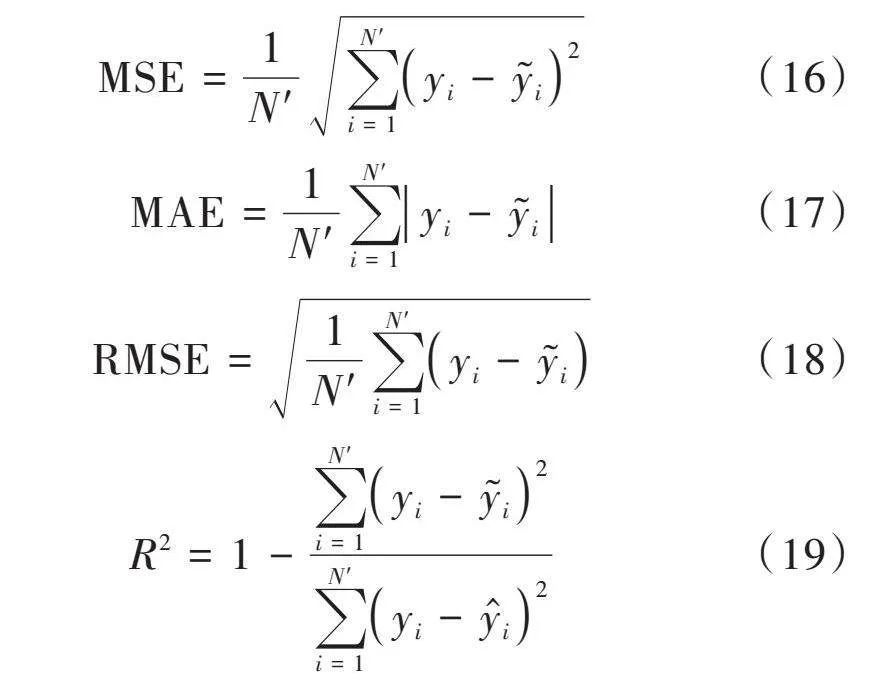
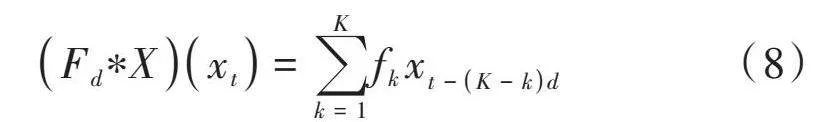
摘" 要： 风力发电作为可再生能源的重要组成部分，在电力系统规划和日常运行中扮演着重要的角色，准确的短期风电功率预测对于电网的稳定运行和优化调度具有重要意义。为提高短期风电功率预测的准确性，提出一种基于自适应噪声完备集合经验模态分解和时间卷积网络的短期风电功率预测方法。首先利用自适应噪声完备集合经验模态分解对初始风电功率数据进行分解，得到多个相对稳定的子数据序列；然后将其分别作为时间卷积网络的输入，利用时间卷积网络模型进行特征提取和功率预测；最后将所有预测值进行汇总，得到最终的功率预测值。使用宁夏某地区真实风电功率数据进行验证，并与传统预测模型比较，结果表明所提方法具有较高的预测精度，可为风电功率短期预测等相关工作提供相关参考。

关键词： 短期风电功率预测； 自适应噪声的完备集合经验模态分解（CEEMDAN）； 时间卷积网络（TCN）； 特征提取； 预测精度； 时间序列分析

中图分类号： TN911.23⁃34" " " " " " " " " " " " "文献标识码： A" " " " " " " " " " " "文章编号： 1004⁃373X（2025）02⁃0097⁃06

Research on short⁃term wind power forecasting based on CEEMDAN⁃TCN

LI Ao， RAN Huajun， LI Linwei， WANG Xinquan， GAO Yue

（College of Electrical Engineering and New Energy， China Three University， Yichang 443002， China）

Abstract： Wind power generation， as an important component of renewable energy， plays a crucial role in power system planning and daily operation. Therefore， accurate short⁃term wind power forecasting is crucial for the stable operation and optimized scheduling of electrical grids. In order to enhance the precision of short⁃term wind power forecasting， a method of short⁃term wind power forecasting based on complete ensemble empirical mode decomposition with adaptive noise （CEEMDAN） and temporal convolutional networks （TCN） is proposed. The CEEMDAN is used to decompose the initial wind power data， so as to obtain multiple several relatively stable sub⁃data sequences. The sub⁃data sequences are used as inputs for TCN， and the TCN model is used to conduct the feature extraction and power forecasting. All predicted values are aggregated to obtain the final power prediction value. The proposed method is verified by the real wind power data from a certain region in Ningxia， and compared with traditional prediction models. The results indicate that the proposed method has high prediction accuracy and can provide relevant references for short⁃term wind power forecasting and other related work.

Keywords： short⁃term wind power forecasting; complete ensemble empirical mode decomposition with adaptive noise; temporal convolutional network; feature extraction; prediction accuracy; time series analysis

0" 引" 言

风能作为一种重要的低碳、可再生能源，在能源行业中获得了广泛的应用[1]。然而，风力发电的高随机性和强波动性给风电并网造成了不利的影响[2]，因此提高风电功率预测的准确性对于电力系统稳定运行具有重要意义。

目前国内外常用的风电功率预测方法主要有物理法、统计法、人工智能法和组合模型法[3]。物理法通过建立风电场及外界环境与风电功率之间的物理模型进行预测[4]，但其受风电机组模型参数和外界环境影响较大，预测精度较低。统计法通过建立风速、风向等历史信息与功率之间的对应关系，实现对未来发电情况的预测，常见预测方法有移动平均法、自回归差分移动平均法[5]、卡尔曼滤波法[6]。统计法可以利用丰富的历史数据对功率的变化趋势进行有效捕捉，但其难以应对数据间复杂的非线性关系和突发事件。人工智能法通过机器学习算法进行预测，如支持向量机[7]、长短期记忆（Long Short Term Memory， LSTM）网络[8]等。随着风电功率预测领域的发展，单一模型的预测精准度明显不能满足当前风电并网要求，组合模型法逐渐被学者们运用到风电功率预测中。文献[9]利用小波分析法对风速的时间序列进行分解，并结合BP神经网络模型实现对未来功率的预测，提高了预测精度。但小波分解法在捕捉非线性和复杂的动态特性时存在一定的局限性。文献[10]通过经验模态分解（Empiricial Mode Decomposition， EMD）对历史风电功率数据进行分解，并利用径向基神经网络进行预测，但EMD可能会出现模态混叠现象，导致预测精度不准确。文献[11⁃12]通过集合经验模态分解（Ensemble Empiricial Mode Decomposition， EEMD）算法对风电功率历史数据进行分解，最后分别利用最小二乘支持向量机（Least Squares Support Vector Machine， LSSVM）和小波神经网络模型进行预测。但EEMD算法在处理信号时依然存在子序列模态混叠问题，且白噪声难以消除。文献[13]将改进的EEMD和最小绝对收缩选择算法与量子回归网络相结合进行功率预测，有效解决了模态混叠问题，但分解子序列中仍存在辅助噪声，影响了预测的精准度。

综上所述，为提高短期风电功率预测的准确性，本文提出一种基于自适应噪声完备集合经验模态分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise， CEEMDAN）和时间卷积网络（Temporal Convolutional Network， TCN）的短期风电功率预测方法。采用CEEMDAN将原始风电功率数据分解为多个相对平稳的子序列，以提高对原始数据信息的提取效果；然后将各个序列分别输入TCN模型进行特征提取和预测；最后将预测结果汇总，得到最终的预测结果。通过将本文所提出的预测方法与其他传统预测方法相比较，得出CEEMDAN⁃TCN模型具有更高的预测精度。

1" 模型原理

1.1" 自适应噪声的完备集合经验模态分解

基于自适应噪声完备集合经验模态分解（CEEMDAN）作为一种具有自适应特点的数据预处理算法，是基于EMD方法的改进。相较于EMD方法，CEEMDAN方法能够不断对可继续分解序列引入有限次的自适应高斯白噪声，然后再对引入白噪声后的序列进行EMD分解，从而有效解决EMD算法易出现波形混叠的问题，并降低重构误差，提高计算效率[13]。该算法将原始风电功率数据分解成一组本征模态函数（Intrinsic Mode Function， IMF）和残差分量（Residual， RES），分解所得的IMF代表了不同尺度上的变化特征[14]，能够很好地处理非线性和非平稳的风电功率数据，并且可以更好地捕捉风电功率数据的局部特性。其算法原理如下：定义[y（t）]为待分解信号，设[Ei（·）]为通过EMD分解后所得到的第[i]个IMF分量，[Ci（t）]是通过CEEMDAN分解所得到的第[i]个IMF，[vk]为满足标准正态分布的高斯白噪声信号，[k=1，2，…，N]为加入白噪声次数，[ε0]为白噪声的标准表，即噪声系数，[r]表示残差分量。

1） 将[N]组正负成对的高斯白噪声加入到待分解信号[y（t）]，得到新信号[y（t）+（-1）qε0vk（t）]，其中[q=1，2]。对新信号进行EMD分解，得到第一阶本征模态分量[C1]。

[E（y（t）+（-1）qε0vk（t））=Ck1（t）+rk] （1）

2） 对产生的[n]个IMF进行总体平均得到CEEMDAN的第1个IMF：

[C1（t）=1Nk=1NCk1（t）] （2）

3） 计算第1个残差[r1（t）]。

[r1（t）=y（t）-C1（t）] （3）

4） 在[r1（t）]中加入正负成对的高斯白噪声得到新信号，并对所得新信号进行EMD分解，得到模态分量[D1]，重复计算[N]次并进行平均，由此可以得到CEEMDAN的第2个IMF：

[C2（t）=1Nk=1NDk1（t）] （4）

5） 计算第2个残差[r2（t）]。

[r2（t）=r1（t）-C2（t）] （5）

6） 重复以上步骤，直到所获得的残差信号为单调信号且不能继续分解，算法结束。此时得到的IMF数量为[m]，则原始信号[y（t）]被分解为：

[y（t）=m=1MCm（t）+rm（t）] （6）

1.2" 时间卷积网络

时间卷积网络（Temporal Convolutional Network， TCN）是一种处理时间序列数据的深度学习模型，相比于LSTM，在参数效率方面因为TCN采用扩张卷积来增加感受野，使得TCN通常具有比LSTM更少的参数。计算效率方面，因TCN通过扩张卷积来捕捉长期依赖，避免了LSTM中的顺序依赖，使得TCN在大规模数据集上的训练更加有效。TCN主要由因果卷积、膨胀因果卷积和残差块三部分构成[15]。

1） 因果卷积。TCN在处理时间序列任务时，要求模型在预测未来值时不能使用未来的信息，即必须保持因果性，因此，TCN采用了一维全卷积网络和因果卷积。假设给定一个序列[X=（x1，x2，…，xt）]，则在[xt]处的因果卷积为：

[F∗Xt=k=1Kfk⋅xt-k+1] （7）

式中：[F=f1，f2，…，fK]为滤波器大小；[K]为滤波器长度；“[∗]”为提取特征信息的卷积操作；[fk]为第[k]个元素的卷积核。

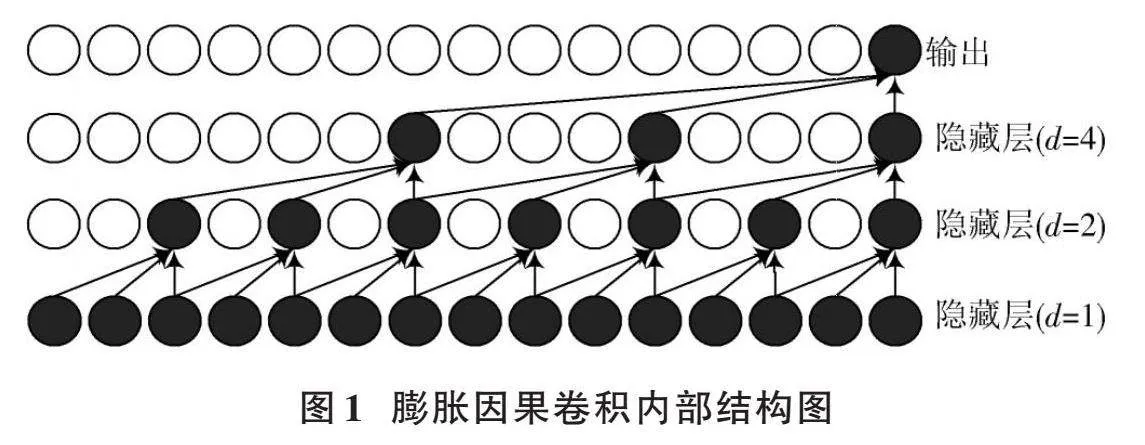
2） 膨胀因果卷积。如上述所知，单一的因果卷积操作依然存在传统卷积神经网络对时间的建模长度受限于卷积核大小的问题，特别是在获取较长时间序列的长期依赖关系时，会因需要堆叠的隐藏层层数增多而出现参数过多的问题。因此，TCN采用了膨胀因果卷积的方法来解决该问题，该卷积方法是在因果卷积映射的基础上增加一个控制卷积操作的参数——膨胀因子来增加感受野，其内部结构图如图1所示。假设给定一个序列[X=x1，x2，…，xt]，则在[xt]处的因果卷积为：

[Fd∗Xxt=k=1Kfkxt-K-kd] （8）

式中[d]为膨胀因子。

3） 残差块。为了解决引入膨胀因果卷积带来的梯度消失或爆炸问题[16]，在TCN的输出层引入残差块，其原理是将模型的输入[x]与输出[Fx]融合，实现跨层传播。TCN残差模块结构如图2所示，引入残差块使得网络不仅仅学习输入数据和输出数据之间的映射关系，还学习输入数据与输出数据之间的残差，最终得到TCN的输出[y]。

[y=Activationx+Fx] （9）

式中[Activation]为激活函数。

1.3" 长短期记忆网络

长短期记忆（LSTM）网络是由Hochreiter提出的一个循环神经网络的变体[17]。LSTM在RNN的基础上引入了控制信息输入的遗忘门、输入门、输出门三种门结构，其算法过程如下：

[ft=σWfht-1，xt+bf] （10）

[it=σWiht-1，xt+bi] （11）

[ot=σWoht-1，xt+bo] （12）

[ct=tanhWcht-1，xt+bc] （13）

[ct=ftct-1+itct] （14）

[ht=ottanhct] （15）

式中：[Wf]、[Wi]、[Wo]、[Wc]分别代表遗忘门、输入门、输出门、记忆单元的权值向量；[bf]、[bi]、[bo]、[bc]分别代表遗忘门、输入门、输出门、记忆单元的偏置向量。

2" 基于CEEMDAN⁃TCN的短期风电功率预测模型

2.1" CEEMDAN⁃TCN模型构建

CEEMDAN⁃TCN模型的结构如图3所示，计算步骤如下。

步骤1：通过CEEMDAN方法对原始风电功率数据进行预处理，以避免原始序列的非平稳性对分析模型产生的负面影响，将其分解为多个稳定的本征模态分量以及1个残差分量。

步骤2：对步骤1所得到的每个子序列进行归一化处理，使用滑动窗口方法对每个子序列建立TCN模型并进行预测，再使用优化算法来调整TCN模型的超参数。

步骤3：将经TCN模型预测后的每个IMF分量和残差分量相加，以得到原始信号的完整预测值。

2.2" 模型评价指标

为定量验证模型的预测效果，本文采用均方误差（Mean Square Error， MSE）、平均绝对误差（Mean Absolute Error， MAE）、均方根误差（Root Mean Square Error， RMSE）、决定系数（R2）对模型的预测精度进行评价。其中，MSE、MAE、RMSE主要用于衡量预测值和实际值之间的差异，其值越小，表明预测值与实际值之间的误差越小，模型预测准确度越高；R2用于评估模型拟合程度，范围为0～1，R2越接近于1，则表明模型预测值与实际值之间的拟合效果越好，预测精准度越高。MSE、MAE、RMSE以及R2的计算公式如下：

[MSE=1N′i=1N′yi-yi2] （16）

[MAE=1N′i=1N′yi-yi] （17）

[RMSE=1N′i=1N′yi-yi] （18）

[R2=1-i=1N′yi-yi2i=1N′yi-yi2] （19）

式中：[N′]为预测样本数量；[yi]为样本真实值；[yi]为样本预测值；[yi]为样本平均值。

3" 算例分析

3.1" CEEMDAN分解

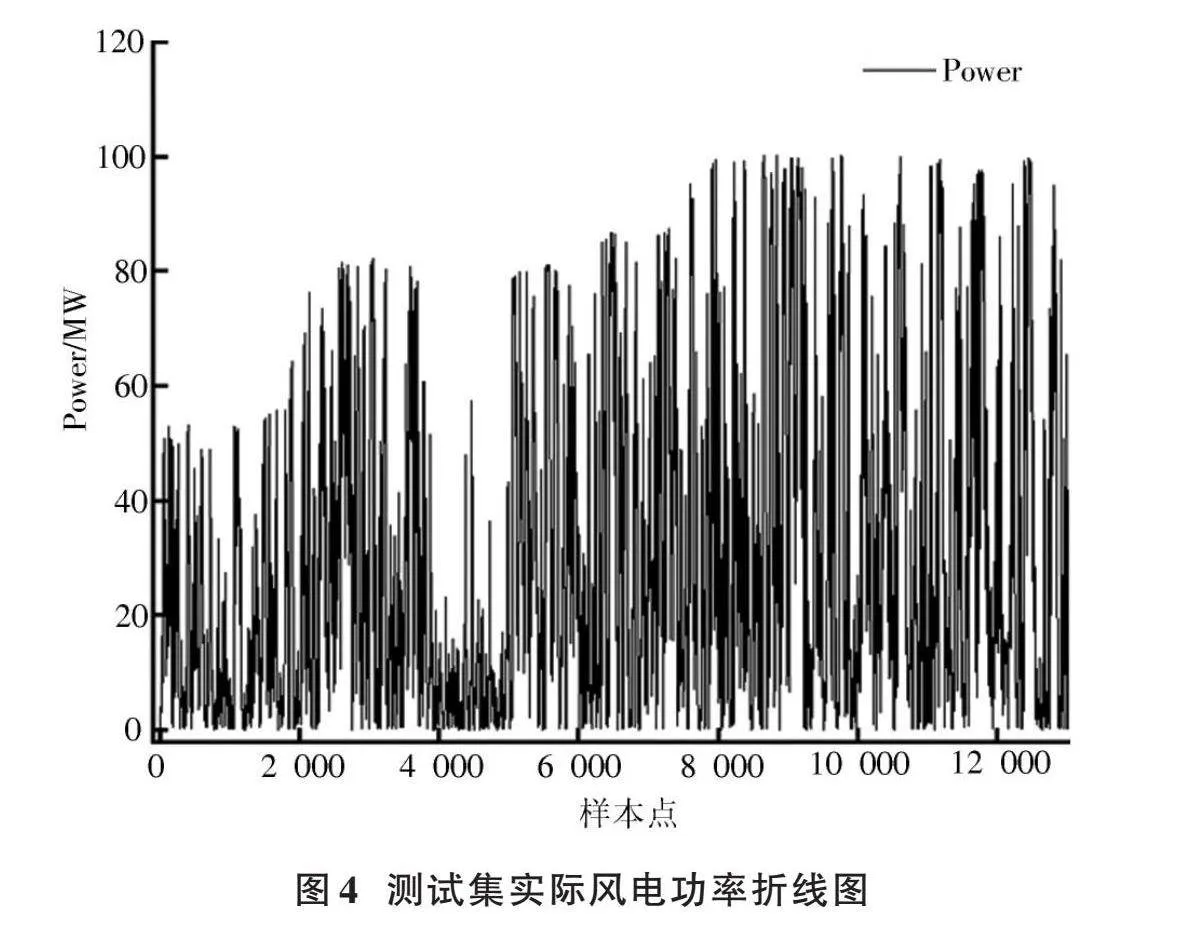
为验证本文所提出的CEEMDAN⁃TCN方法对风电功率预测的可行性，以宁夏某风电场为研究对象，采集时间跨度为2021⁃01⁃01T00：00—2021⁃06⁃01T23：45的风电功率数据，设定每15 min进行一次数据采样，对数据进行预处理后，删除风电功率为0 MW的数据，得出风电功率时间序列曲线，如图4所示，共计12 988组数据，其中训练集为10 182组，验证集为2 546组，测试集为260组。

选用CEEMDAN方法对处理后的风电功率序列进行分解，得到12个IMF分量和1个RES分量，分解结果如图5所示，明显可以看出风电功率数据经CEEMDAN方法分解后，所得出的子数据序列波逐渐趋于平缓。因此，CEEMDAN分解能够有效降低风电功率序列的非平稳性，更加有利于后续模型的处理工作。

3.2" TCN模型参数设置

为提高TCN模型的预测精度，本文采用控制变量，根据预测结果调整TCN模型参数，最终将TCN模型滤波器数量设定为64，卷积核大小设定为2，膨胀因子设定为1、2、4、8，模型优化算法采用Adam，初始学习率设定为0.001，迭代次数设定为100。对比模型LSTM参数与TCN模型参数设定相似，迭代次数也为100次。本文开发环境为Python 3.9，Tensorflow版本为2.12.0。

3.3" 对比分析

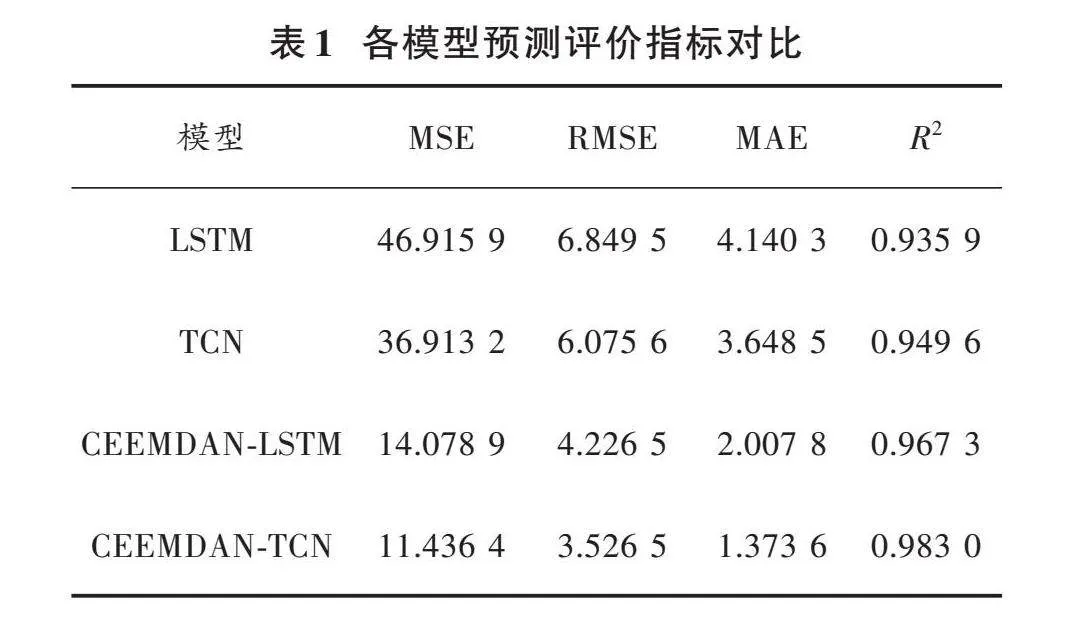
为了证实本文所提出的CEEMDAN⁃TCN组合模型对于风电功率预测的有效性与准确性，研究选用了TCN模型、LSTM模型以及结合CEEMDAN的LSTM模型（CEEMDAN⁃LSTM）3种预测模型作为对照组进行对比实验分析，采用MSE、RMSE、MAE、R2指标对4种模型的预测结果进行评价，结果如表1所示，预测值和真实值对比结果如图6所示。

由表1可知，4种模型均具有较好的预测效果，但与TCN、LSTM和CEEMDAN⁃LSTM三种模型相比，本文所提出的CEEMDAN⁃TCN模型的MSE、RMSE和MAE评价指标值明显更低，R2的值更接近于1，模型拟合效果更好，预测精度得到了明显的提升。其次，结合图6可知，TCN模型的预测效果优于LSTM模型，相较于LSTM模型，MSE降低了21.32%，RMSE降低了11.30%，MAE降低了11.88%，R2上升了1.46%，说明与LSTM模型相比，TCN模型具有更强大的特征提取和拟合能力，但是相比于另外两种组合模型，单一的TCN模型在峰值和低谷的预测能力明显欠佳，因此对于突发事件的预测会有较大偏差。

CEEMDAN⁃LSTM模型相较于单一的LSTM模型，预测效果明显提升，MSE、RMSE和MAE分别降低了69.99%、38.29%和51.50%，R2上升了3.36%，并且CEEMDAN⁃LSTM模型对于功率峰值的预测较好，但对于波谷的波动仍无法进行有效的预测。

而本文所提出的CEEMDAN⁃TCN模型相较于LSTM、TCN和CEEMDAN⁃LSTM三种模型，MSE分别减少了75.62%、69.02%、18.77%，RMSE分别减少了48.51%、41.96%、16.56%，MAE分别减少了66.82%、62.35%、31.59%，R2分别上升了5.03%、3.52%、1.62%。并且由预测值与真实值的对比图可知，CEEMDAN⁃TCN预测精度最高，对功率峰值和波谷方面的预测依然具有较好的预测效果，能够更加准确地预测突发事件。综上所述，本文所提方法在短期风电功率预测方面具有一定的优越性。

4" 结" 语

本文针对风电功率数据高随机性和强波动性导致预测精度不高的问题，将自适应噪声的完备集合经验模态分解和时间卷积网络结合，提出一种基于CEEMDAN⁃TCN的短期风电功率预测方法，通过实验分析得出以下结论。

1） 通过CEEMDAN将非线性、非平稳性的风电功率数据分解为较为稳定的子序列，降低了原始风电功率序列数据的不稳定性，从而有效提升了数据质量，使后续进行特征提取和预测的效果得到明显提高。

2） 通过对比TCN模型和LSTM模型的预测结果，得出TCN模型具有更强的特征提取和预测能力，但对于功率峰值和波谷的预测效果较差。

3） 在短期风电功率预测方面，本文所提出的CEEMDAN⁃TCN模型相较于LSTM、TCN、CEEMDAN⁃LSTM模型预测精度最高，预测效果最好，对功率峰值和波谷的预测也同样最准确，说明了该模型在短期风电功率预测方面的有效性。

注：本文通讯作者为李敖。

参考文献

[1] 周孝信，陈树勇，鲁宗相，等.能源转型中我国新一代电力系统的技术特征[J].中国电机工程学报，2018，38（7）：1893⁃1904.

[2] 程海花，寇宇，周琳，等.面向清洁能源消纳的流域型风光水多能互补基地协同优化调度模式与机制[J].电力自动化设备，2019，39（10）：61⁃70.

[3] 杨国华，祁鑫，贾睿，等.基于CEEMD⁃SE的CNNamp;LSTM⁃GRU短期风电功率预测[J].中国电力，2024，57（2）：55⁃61.

[4] 牛东晓，纪会争.风电功率物理预测模型引入误差量化分析方法[J].电力系统自动化，2020，44（8）：57⁃65.

[5] 丁藤，冯冬涵，林晓凡，等.基于修正后ARIMA⁃GARCH模型的超短期风速预测[J].电网技术，2017，41（6）：1808⁃1814.

[6] 秦磊，董海鹰，王润杰.基于卡尔曼滤波和模型预测控制的混合储能平抑风电功率波动策略[J].电网技术，2024，48（10）：4286⁃4297.

[7] HABIB A， ABBASSI R， ARISTIZÁBAL J A， et al. Forecasting model for wind power integrating least squares support vector machine， singular spectrum analysis， deep belief network， and locality‐sensitive hashing [J]. Wind energy， 2020， 23（2）： 235⁃257.

[8] 王炜，刘宏伟，陈永杰，等.基于LSTM循环神经网络的风力发电预测[J].可再生能源，2020，38（9）：1187⁃1191.

[9] 陶虎，文智江，吴晓锐.基于小波分析和改进BP神经网络的风电功率预测算法[J].广西电力，2022，45（2）：1⁃6.

[10] 王佶宣，邓斌，王江.基于经验模态分解与RBF神经网络的短期风功率预测[J].电力系统及其自动化学报，2020，32（11）：109⁃115.

[11] 王贺，胡志坚，陈珍，等.基于集合经验模态分解和小波神经网络的短期风功率组合预测[J].电工技术学报，2013，28（9）：137⁃144.

[12] LIANG Z T， LIANG J， ZHANG L， et al. Analysis of multi⁃scale chaotic characteristics of wind power based on Hilbert⁃Huang transform and Hurst analysis [J]. Applied energy， 2015， 159： 51⁃61.

[13] HE Y Y， WANG Y. Short⁃term wind power prediction based on EEMD⁃LASSO⁃QRNN model [J]. Applied soft computing， 2021， 105： 107288.

[14] 宿磊，沈煜，杨帆，等.融合CEEMDAN分解与敏感IMF精选的串联电弧故障检测[J].电子测量与仪器学报，2022，36（10）：173⁃180.

[15] GAO B， HUANG X， SHI J， et al. Hourly forecasting of solar irradiance based on CEEMDAN and multi⁃strategy CNN⁃LSTM neural networks [J]. Renewable energy， 2020， 162： 1665⁃1683.

[16] LIU Q， CHE X， BIE M. R⁃STAN： residual spatial⁃temporal attention network for action recognition [J]. IEEE access， 2019（7）： 82246⁃82255.

[17] PRASHANT K， ANANDA S H. Dilated convolutional neural network based model for bearing faults and broken rotor bar detection in squirrel cage induction motors [J]. Expert system application， 2022， 191： 116290.

[18] HU C J， ZHAO Y， JIANG H， et al. Prediction of ultra⁃short⁃term wind power based on CEEMDAN⁃LSTM⁃TCN [J]. Energy reports， 2022， 8： 483⁃492.