基于参数优化变分模态分解的信号降噪方法

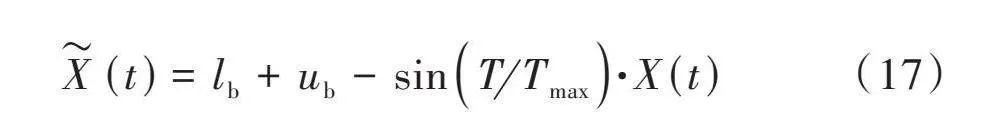
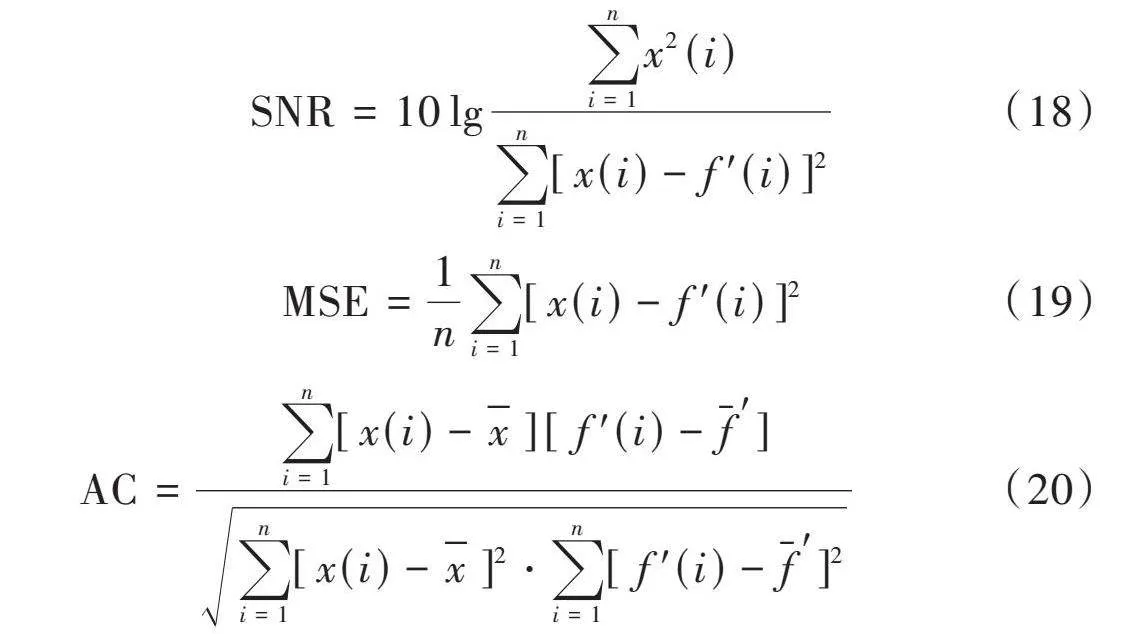
摘" 要： 针对心电信号中肌电干扰噪声难以去除的问题，提出一种基于参数优化变分模态分解（VMD）的信号降噪方法。通过设计动态边界策略和反向种群生成方式，对白鲸优化（BWO）算法进行改进；采用改进白鲸优化算法对VMD参数自适应寻优，确定分解层数K与惩罚因子α；对含噪心电信号进行分解，得到k个本征模态函数（IMF）分量，同时采用相关系数法进行有效模态和含噪模态识别；对噪声主导的模态分量采用小波阈值降噪，并重构信号主导模态与降噪后模态。对仿真信号与含真实肌电干扰的心电信号进行降噪处理，实验结果表明，所提方法去噪效果优于小波阈值去噪法、EMD法、EMD⁃小波阈值去噪法，真实含噪的心电信号经该方法去噪后自相关系数可达0.91以上。

关键词： 变分模态分解； 信号降噪； 参数优化； 改进白鲸优化算法； 心电信号； IMF分量； 小波阈值降噪； 肌电干扰

中图分类号： TN911.7⁃34" " " " " " " " " " " " " "文献标识码： A" " " " " " " " " " " 文章编号： 1004⁃373X（2025）02⁃0070⁃07

Method of signal denoising based on parameter⁃optimized VMD

HE Yujie1， 2， LI Xin’e1， 2， HE Jun1， 2

（1. State Key Laboratory of Dynamic Measurement Technology， North University of China， Taiyuan 030051， China;

2. School of Electrical and Control Engineering， North University of China， Taiyuan 030051， China）

Abstract： In allusion to the problem of difficult removal of electromyographic interference noise in electrocardiogram （ECG） signals， a method of signal denoising based on parameter⁃optimized variational mode decomposition （VMD） is proposed. The beluga whale optimization （BWO） algorithm is improved by designing the dynamic boundary strategy and inverse population generation. The improved BWO algorithm is used for the adaptive optimization of the VMD parameters to determine the number of decomposition layers K and the penalty factor α. The noise⁃containing ECG signal is decomposed to obtain k intrinsic mode function （IMF） components， and the correlation coefficient method is used to identify the effective modes and noise⁃containing modes. The noise⁃dominated modal components are noise⁃reduced by means of the wavelet thresholding， and the dominant modes and noise⁃reduced modes of the reconstructed signal are reconstructed. The simulation signals and ECG signals with real EMG interference are processed for the denoising. The experimental results show that the proposed method is superior to wavelet threshold denoising method， EMD method and EMD⁃wavelet threshold denoising method， and the autocorrelation coefficient of real ECG signals with noise can reach more than 0.91 after denoising.

Keywords： variational modal decomposition; signal denoising; parameter optimization; improved beluga optimization algorithm; ECG signal; IMF component; wavelet threshold denoising; electromyogrophic interference

0" 引" 言

心电信号（Electrocardiogram， ECG）是诊断人体心血管疾病最为重要的生理参数之一，对心电信号的处理和分析具有极其重要的实用价值[1]。然而心电信号是一种微弱、非线性、非平稳的生理信号，在采集过程中，易受到被测者肌肉收缩所产生的肌电噪声的干扰。肌电干扰信号频带较宽，频率[2]通常为5～500 Hz，极易与心电信号发生频谱混叠，因此成为心电信号去噪领域的难点问题。

心电信号肌电干扰的去除，目前常用的去噪方法有：小波阈值去噪法、经验模态分解（Empirical Mode Decomposition， EMD）、变分模态分解（Variational Mode Decomposition， VMD）等。

小波阈值去噪法具有计算速度快、信号保留完整等特点，得到了广泛应用[3]，但其易受小波基选取和阈值函数选取的影响。文献[4]针对小波阈值去噪中传统软、硬阈值的不足，提出了一种改进的阈值函数，并将其应用在心电信号的肌电干扰去除中。文献[5]提出了一种小波基的选择程序，在心电信号去噪过程中，同时保持信号峰值接近其全振幅，对信号峰值等特征点进行保留。

EMD可以将信号自适应地分解为若干本征模态函数（Intrinsic Mode Function， IMF）[6]。文献[7]采用EMD联合小波阈值去噪对心电信号中的噪声信号进行去除。文献[8]采用EMD结合各IMF分量的统计学特性进行心电信号去噪。但是EMD在信号分解过程中存在模态混叠，使得信号中特征频率与噪声的分离程度不足。

VMD将信号分解成不同频率占优的子信号，进而分析信号[9]，有效解决了模态混叠问题。利用VMD进行信号处理时，分解层数K和惩罚因子α的值需预先设定，且K与α的值对分解效果有很大影响。目前确定K与α的方法主要有三种：一是根据先验知识或中心频率观察法[10]，该方法需要多次尝试，效率较低且适应性较差；二是评价指标选取法[11]，根据信号特征建立合适的评价指标进行参数选取，但此方法选取出的K值不具有普遍性；三是优化算法选取法[12]，通过各类元启发式算法（如粒子群算法、鲸鱼优化算法）进行自适应寻优，得到相应参数。通过优化算法搜索得到VMD参数，通常需要大量的迭代计算，在实际应用过程中，如何提高优化算法的精度，避免陷入局部最优，是需要解决的问题。

针对以上问题，本文提出了一种基于参数优化变分模态分解的信号降噪方法。首先本文提出了一种改进白鲸优化（Improved Beluga Whale Optimization， IBWO）算法，实现对VMD中分解层数K与惩罚因子α自适应寻优。该算法设计了动态边界条件与反向种群生成方式，提高了IBWO的搜索能力，又避免陷入局部最优；基于最优K与α，对信号进行变分模态分解；采用相关系数法对各IMF分量进行判别，对噪声主导的IMF分量采用小波阈值去噪法处理；最后将所有分量重构，得到降噪后的信号。

1" 相关理论

1.1" 变分模态分解（VMD）

变分模态分解是一种借助Hilbert⁃Huang变换、频率混合等技术的信号分解方法，能够将输入信号分解为k个模态分量，每个分量都具有确定的中心频率和有限的带宽，具体原理如下。

每个模态的单边谱可以通过计算与待分解信号相关的模态的Hilbert变换来获取：

[δt+jπt·ukt] （1）

通过引入指数项来调整模态函数的中心频率，将每个模态的频谱转移至基带：

[δt+jπt·ukte-jωkt] （2）

变分模态分解可以被描述为一个带有约束条件的最优化问题，具体形式如下：

[minuk，ωkk∂tδt+jπt·ukte-jωkt22s.t." "kuk=f] （3）

为了寻求变分约束模型的最优解，引入了Lagrange乘数λ算子和二次惩罚函数项α，构建增广Lagrange函数：

[Luk，ωk，λ=αk∂tδt+jπt·ukte-jωkt22+ft-kukt22+λt，ft-kukt]

（4）

迭代后的最优解为：

[un+1k（ω）=f（ω）-i≠kun+1i（ω）+λn（ω）21+2α（ω-ωnk）2] （5）

[ωn+1k=0∞ωun+1kω2dω0∞un+1kω2dω] （6）

[λn+1ω=λnω+βfω-kun+1kω] （7）

1.2" 白鲸优化算法

白鲸优化算法（Beluga Whale Optimization，BWO）是由文献[13]提出的一种元启发式智能优化算法，该算法受白鲸捕食过程的启发而建立，具有全局勘探、局部开发和鲸落三个阶段。算法首先对白鲸位置进行初始化，由参数[Bf]决定算法执行勘探阶段还是开发阶段，[Bf]公式如下：

[Bf=B01-T2Tmax] （8）

式中：T为当前迭代次数；[Tmax]为最大迭代次数；[B0]为（0，1）的变化值。当[Bf]gt;0.5时执行勘探阶段，否则执行开发阶段。

全局勘探阶段位置更新按照j的奇偶性而有所不同，当j为偶数时，位置更新公式为：

[XT+1i，j=XTi，Pj+（XTr，P1-XTr，Pj）（1+r1）sin2πr2] （9）

式中：Pj是从d维中选择的随机数；r1和r2是（0，1）之间的随机数。当j为奇数时，式（9）中的正弦函数变为余弦函数。局部开发阶段位置更新公式为：

[XT+1i=r3XTbest-r4XTi+C1⋅LF⋅（XTr-XTi）] （10）

[C1=2r4（1-TTmax）] （11）

式中：[XTbest]是白鲸中的最佳位置；r3和r4是（0，1）的随机数；C1是测量Lévy飞行强度的随机跳跃强度；LF是Lévy飞行函数。

鲸鱼坠落阶段位置更新公式为：

[XT+1i=r5XTi-r6XTr+r7Xstep] （12）

式中：r5、r6、r7均为（0，1）的随机数；Xstep是白鲸坠落的步长。[Xstep]公式为：

[Xstep=（ub-lb）exp-C2TTmax] （13）

[C2=2Wf·n] （14）

[Wf=0.1-0.05TTmax] （15）

式中：C2是与白鲸坠落概率和种群规模有关的阶跃因子；ub和lb分别是变量的上下界；Wf为鲸鱼坠落概率。

2" 改进白鲸优化算法

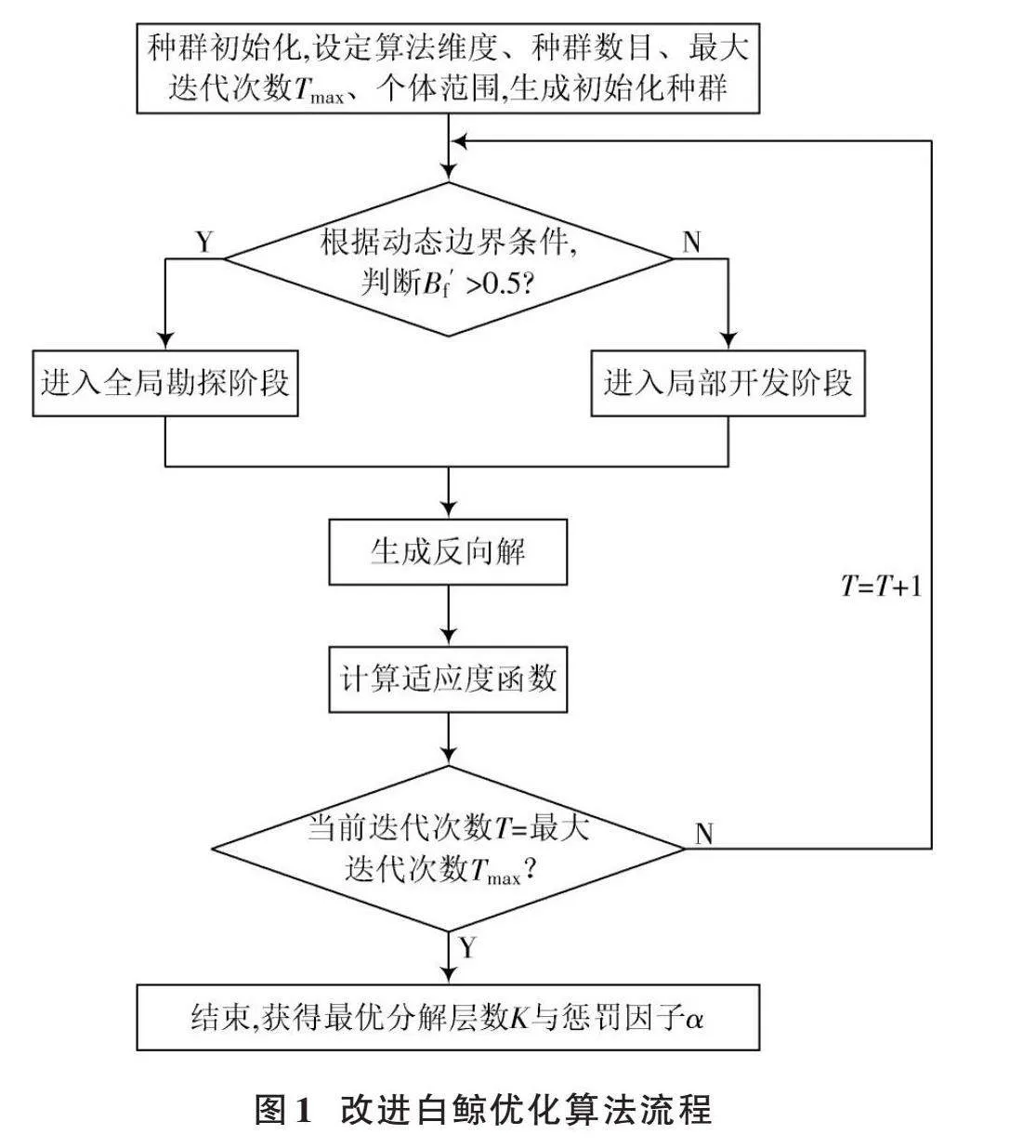
本文提出一种改进的白鲸优化（IBWO）算法，通过设计动态边界条件与反向种群生成方式对白鲸优化算法进行改进。IBWO算法流程如下。

1） 算法初始化。设定算法维度为2，分别对应分解层数K与惩罚因子α。根据信号特征设置种群个数、迭代次数和个体范围，并随机生成初始化种群。

2） 根据动态边界条件判断是执行勘探阶段还是开发阶段。本文引入余弦因子，将边界条件设置为式（16），将权重设为非线性递减形式，递减速度先快后慢，[B'f]大于0.5时执行勘探阶段，否则执行局部开发阶段。引入非线性动态边界条件，使得算法前期重点关注全局勘探，后期重点关注局部开发，更好地平衡勘探与开发阶段，有利于提高算法的精度，并防止算法出现早熟现象。

[B'f=B0⋅cosπT2Tmax] （16）

3） 生成反向种群。为防止算法陷入局部最优，在当前种群的基础上生成反向种群，同时考虑当前解和反向解，有利于算法跳出局部最优。在生成反向种群时，由于迭代前期种群质量较低，因此基于当前种群生成的反向种群质量也较低。基于此，在生成反向种群过程中引入动态权重因子，权重因子为正弦函数，如公式（17）所示。算法迭代初期权值较小，迭代后期权值较大，可以更好地引导反向解的生成，有助于算法跳出局部最优，提高算法精度。

[X（t）=lb+ub-sinTTmax·X（t）] （17）

4） 计算适应度函数。以信号的最小包络熵为适应度函数，进行适应度计算，最小包络熵值越小，说明分解效果越好。将当前解与步骤3）生成的反向解进行适应度排序，选择适应度最小的个体作为最优个体。

5） 判断是否到达最大迭代次数，若未到达则进行下一次迭代；若已到达最大迭代次数，则将最优个体的位置输出，即为分解层数K与惩罚因子α的值。

IBWO算法流程如图1所示。

3" 去噪方法及指标

3.1" 去噪方法

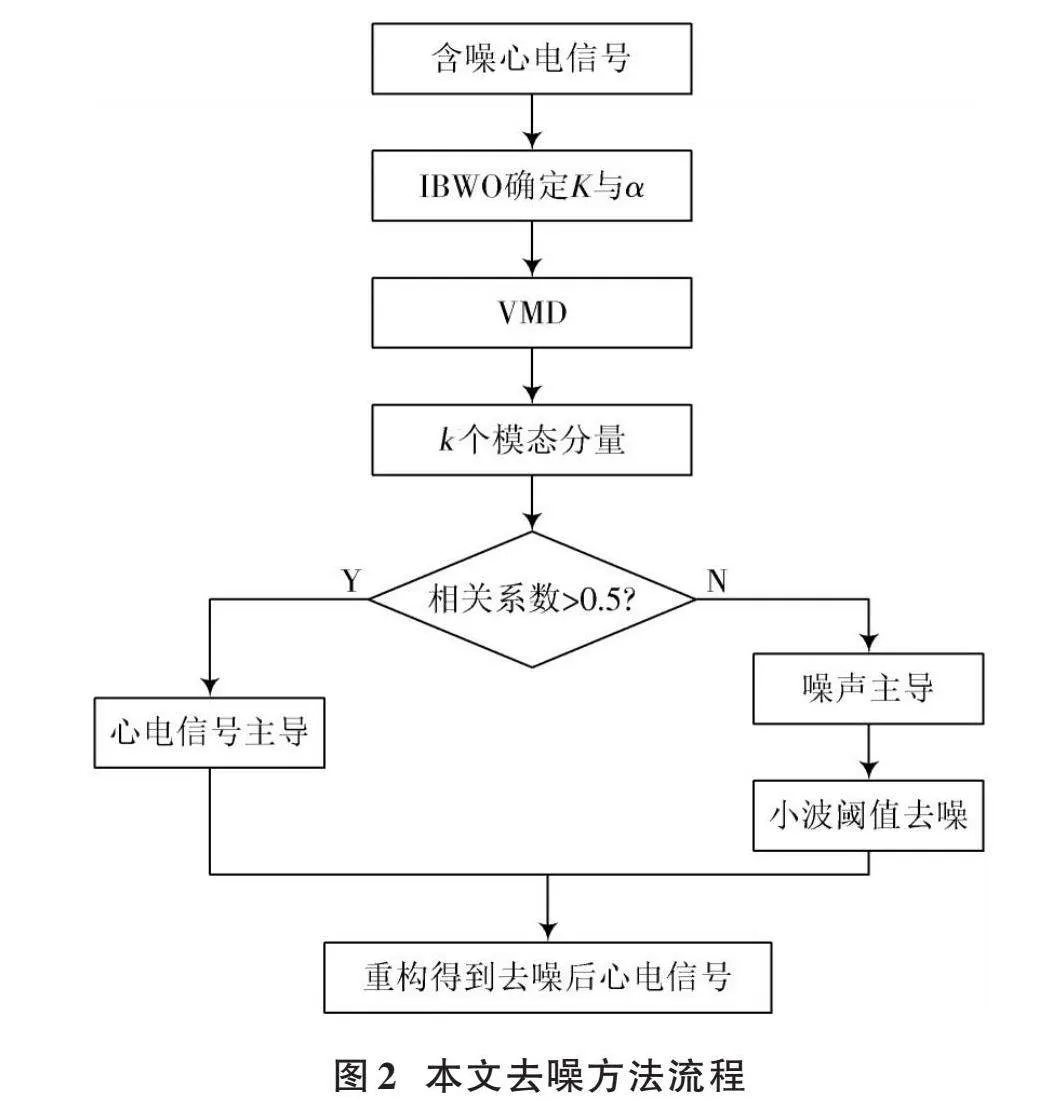
结合VMD的特点，本文采用IBWO确定VMD中的分解层数K和惩罚因子α，确定参数后对ECG进行VMD，对得到的每一个IMF分量计算其相关系数，相关系数大于0.5的信号认为由ECG主导，否则认为由噪声主导。利用小波阈值去噪对噪声主导的信号进行降噪处理，最后将所有IMF分量进行重构，得到降噪后的ECG。

IBWO⁃VMD参数优化的具体步骤如下。

1） 初始化IBWO参数。

2） 在规定的范围内随机生成初始化群体，初始化IBWO。

3） IBWO开始迭代，计算适应度函数，寻找最优的分解层数K和惩罚因子α。

4） 对含噪ECG进行K层VMD。

5） 对VMD得到的k个IMF分量进行相关系数的计算，相关系数大于0.5的IMF分量认为是ECG主导，否则认为是噪声主导的分量。

6） 对判断为噪声主导的IMF分量采用小波阈值去噪进行去噪处理。

7） 将由ECG主导的IMF分量和去噪后的噪声主导IMF分量进行重构，得到去噪后的ECG。

本文去噪方法流程如图2所示。

3.2" 评价指标

为了全面评估在ECG肌电干扰去噪中本文方法的有效性，使用了三个评价指标：信噪比（Signal to Noise Ratio， SNR）、均方误差（Mean Square Error， MSE）和自相关系数（Autocorrelation Coefficient， AC），用于判断去噪后信号与原始信号的相似程度。

[SNR=10lgi=1nx2（i）i=1n[x（i）-f'（i）]2] （18）

[MSE=1ni=1n[x（i）-f'（i）]2] （19）

[AC=i=1n[x（i）-x][f'（i）-f']i=1n[x（i）-x]2⋅i=1n[f'（i）-f']2] （20）

式中：[x（i）]代表无噪声的原始ECG；[f'（i）]代表经过去噪处理后的ECG。[SNR]越大，MSE越小，表示去噪后的信号与无噪声信号相似程度越高，去噪效果越好。AC越大，表明经过去噪后重构的ECG与原始ECG之间的偏差越小，去噪效果越好。

4" 仿真实验与实测验证

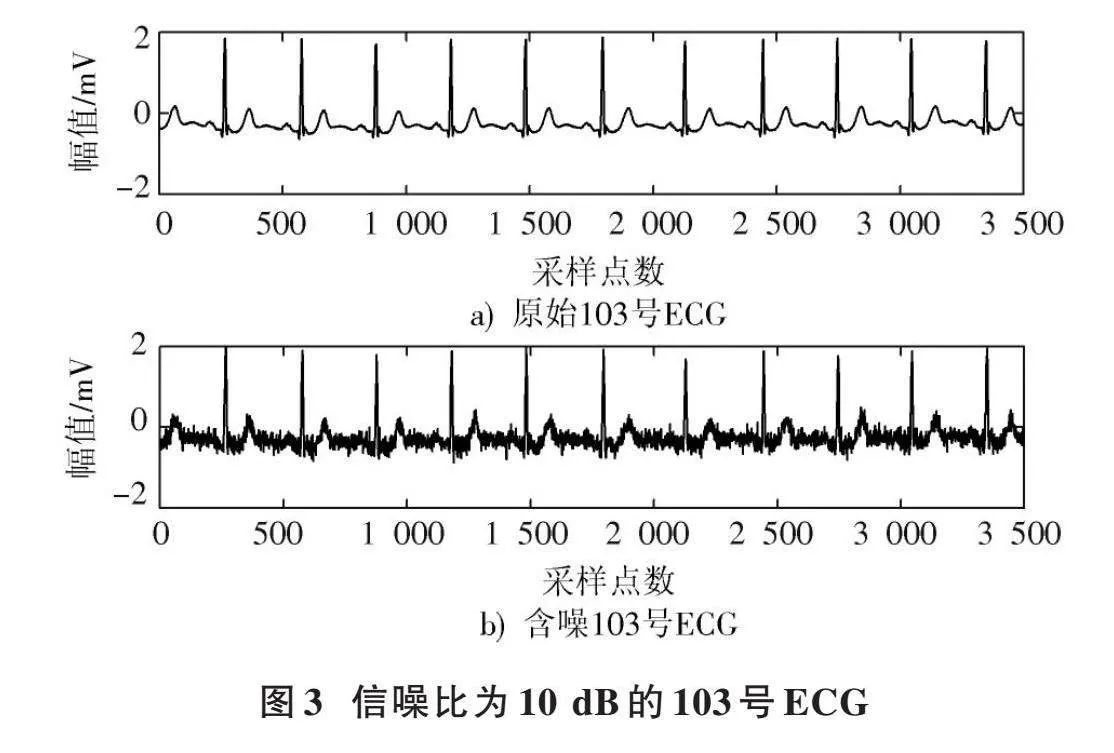
ECG的肌电干扰噪声可以看作一种有限带宽的高斯白噪声，先前的研究常常使用可控的高斯白噪声来模拟肌电干扰进行相关分析[14]。本文选择来自“MIT⁃BIH Arrhythmia Database”的103号ECG。将103号ECG叠加信噪比为10 dB的高斯白噪声，产生含噪103号ECG。分别采用小波阈值去噪法、EMD、EMD⁃小波阈值去噪法及本文方法对含噪的103号ECG进行去噪，并将处理结果进行对比分析。图3为信噪比为10 dB的103号ECG。

4.1" 仿真实验

将仿真103号ECG作为IBWO的输入来选取VMD参数，最终得到的最优参数为K=7，α =1 200。

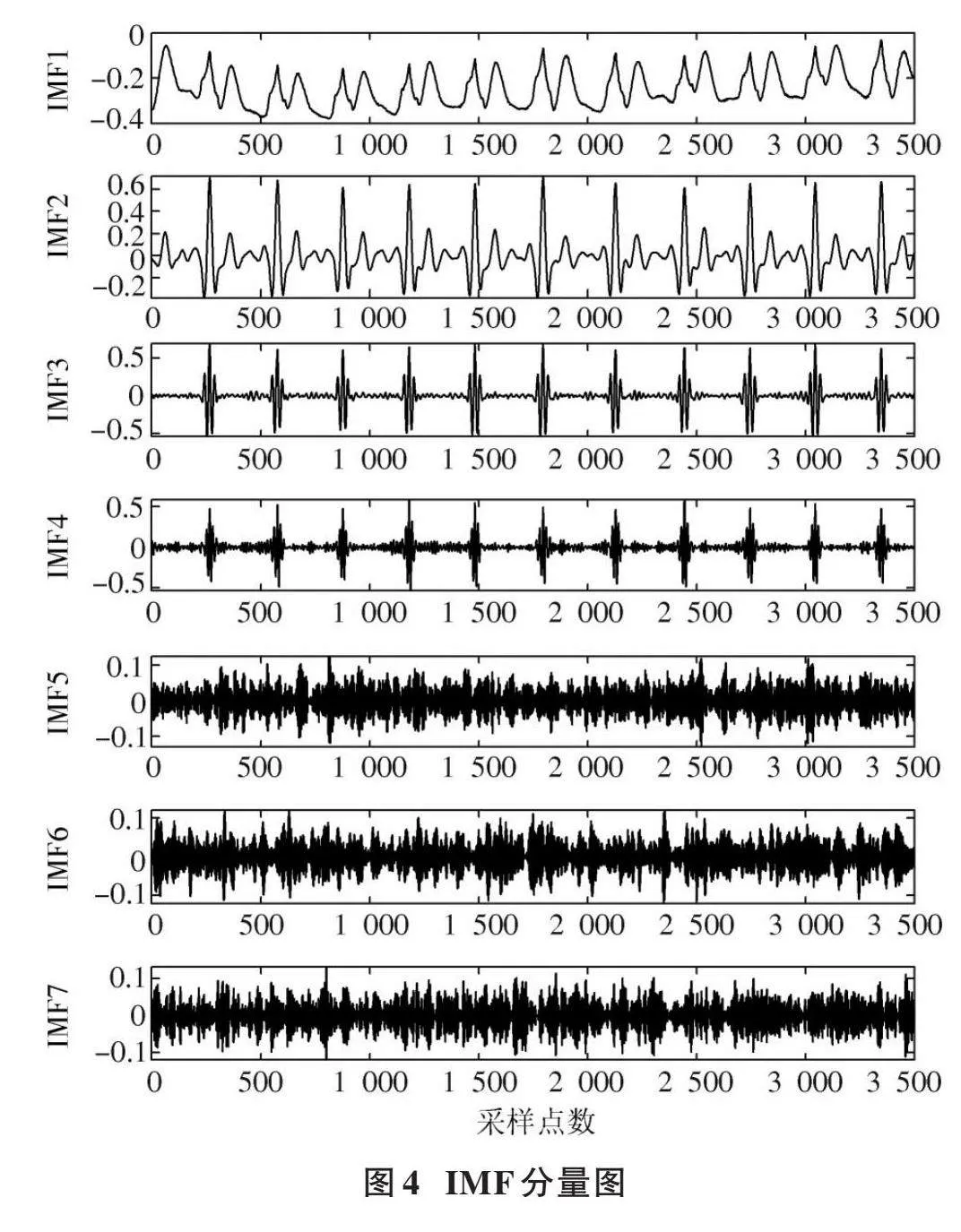
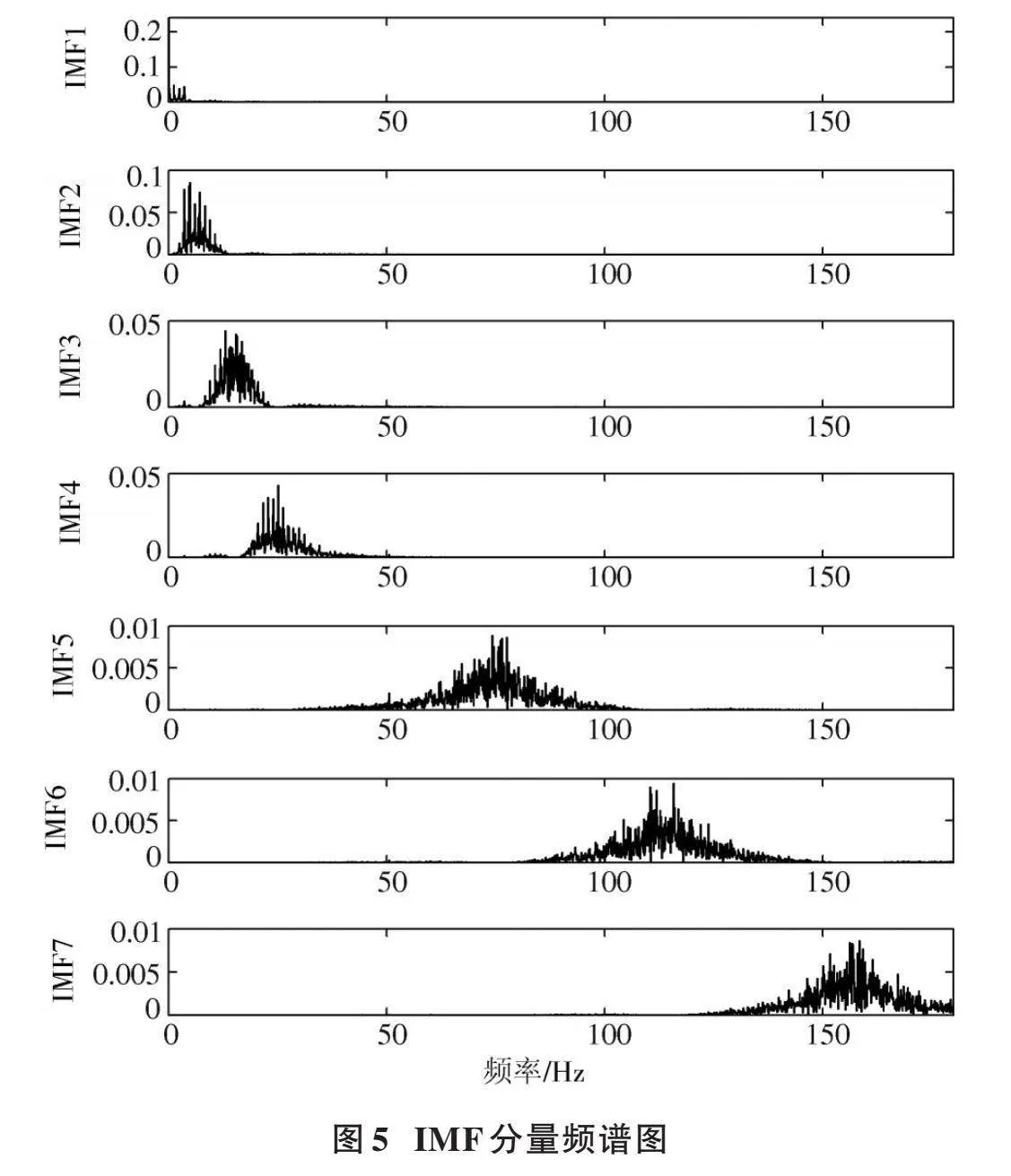
经过IBWO⁃VMD处理后，103号ECG被分解为7个IMF分量，如图4所示，各IMF分量的频谱如图5所示。

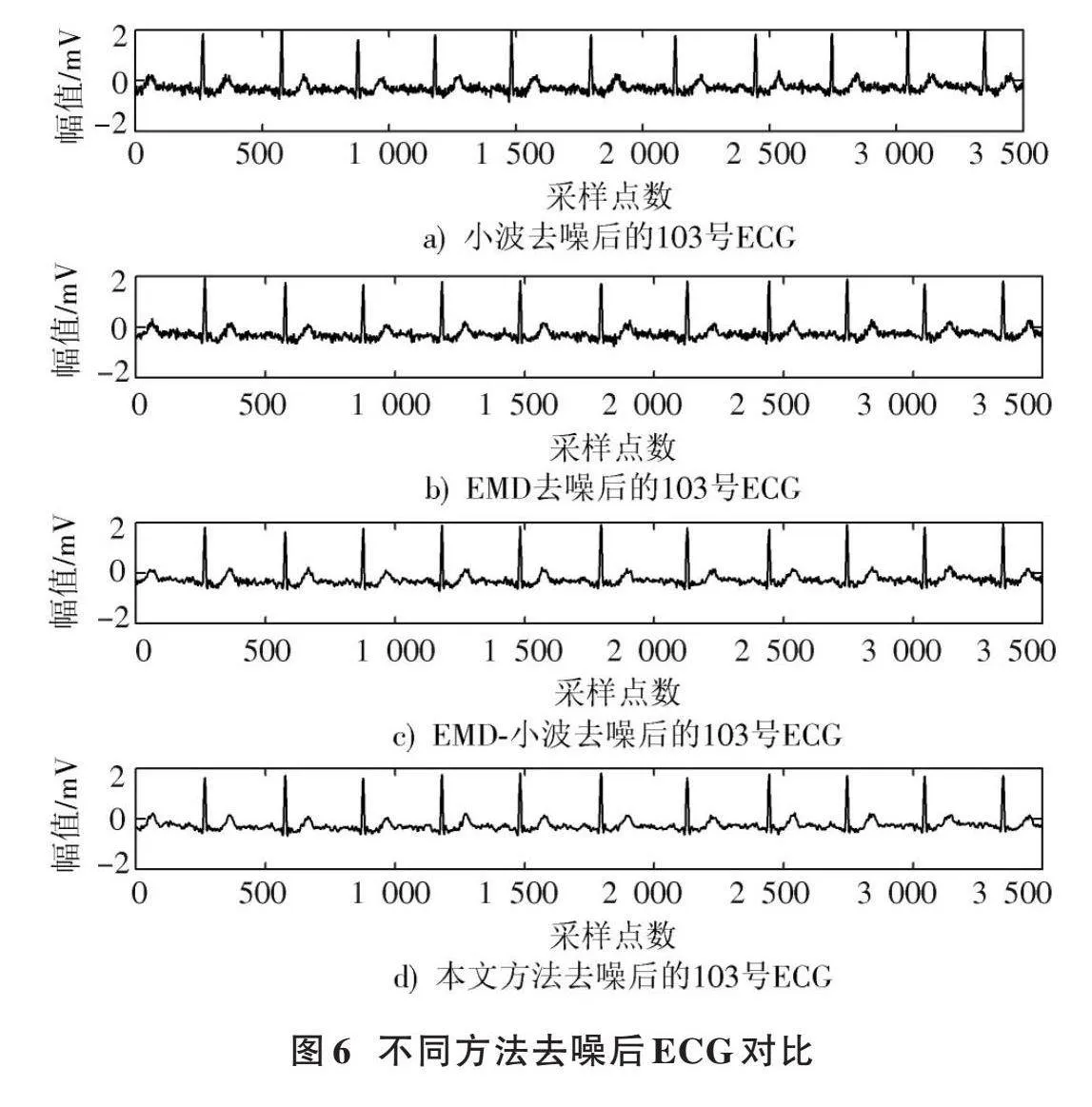
计算每个IMF分量与原始心电信号的相关系数，这7个IMF分量的相关系数依次为0.507 8、0.734 6、0.621 4、0.423 7、0.017 5、0.005 0、0.002 3。IMF1～IMF3分量的相关系数均大于0.5，而IMF4～IMF7分量的相关系数均小于0.5。因此，认为IMF1～IMF3由ECG主导，IMF4～IMF7由噪声信号主导。对噪声主导的IMF4～IMF7分量进行小波阈值去噪处理，将去噪后的IMF4～IMF7分量与ECG主导的IMF1～IMF3分量进行重构，即可得到去噪后的103号ECG。采用不同方法对信号进行去噪处理，各方法重构后的103号ECG见图6。

由图6可知：经本文方法去噪后，有效地去除了肌电干扰信号；相比其他去噪方法，本文方法去噪后的103号ECG较多地保留了原始ECG的信号特征，更好地对原始ECG进行了还原。

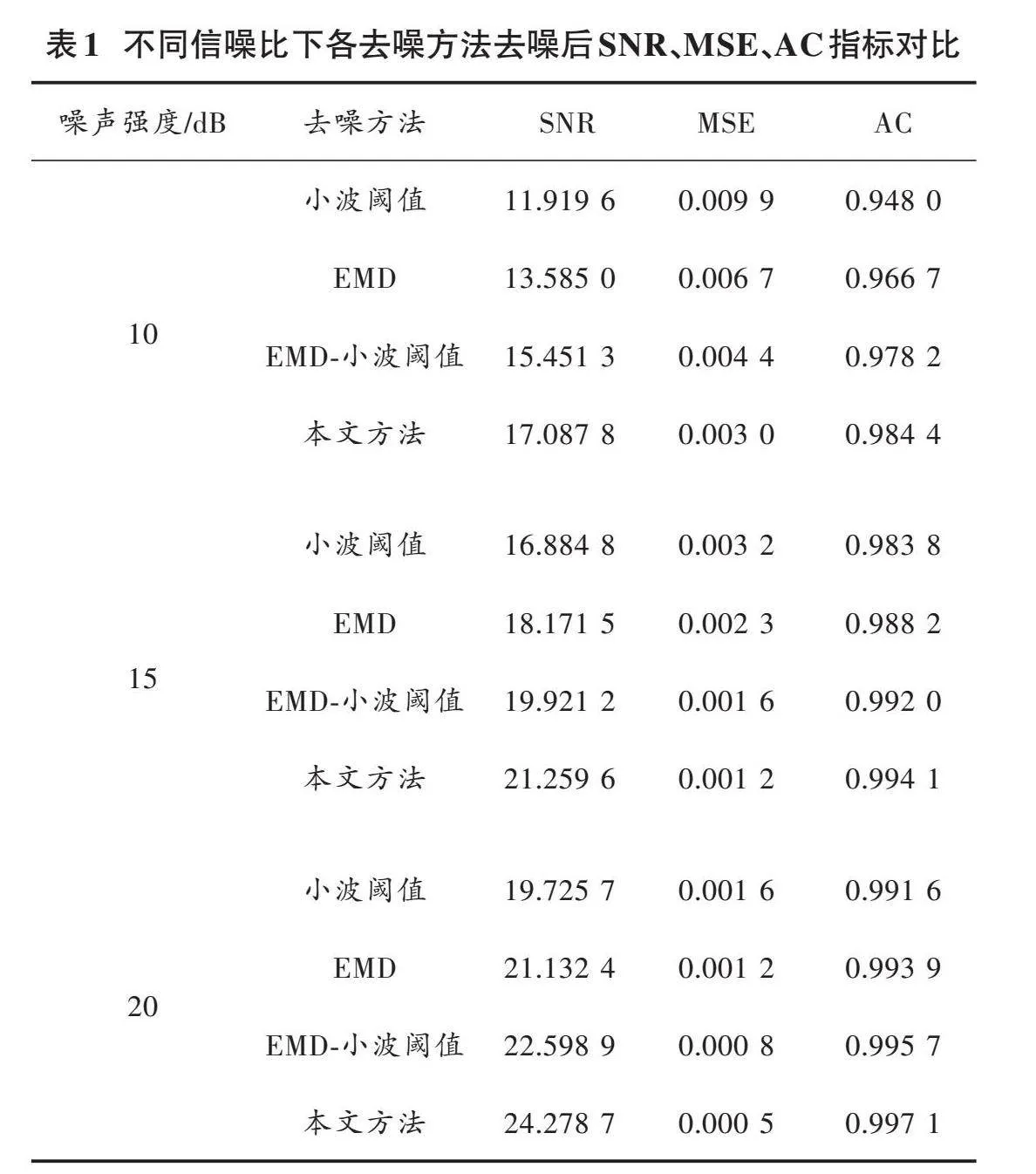
为进一步验证本文所提去噪算法的去噪能力，在103号ECG中再添15 dB、20 dB高斯白噪声进行分析验证，对不同信噪比的噪声分别采用小波阈值去噪、EMD、EMD⁃小波阈值去噪、本文方法进行验证与对比。不同信噪比下各去噪方法去噪后[SNR]、MSE、AC等比较指标如表1所示。

从表1可以看出，本文方法相较于其余三种去噪方法，拥有更大的SNR和AC，以及更小的MSE。表明经本文去噪方法重构的ECG与原始ECG相似度较高，证明了本文方案的可行性。

4.3" 实测ECG实验分析

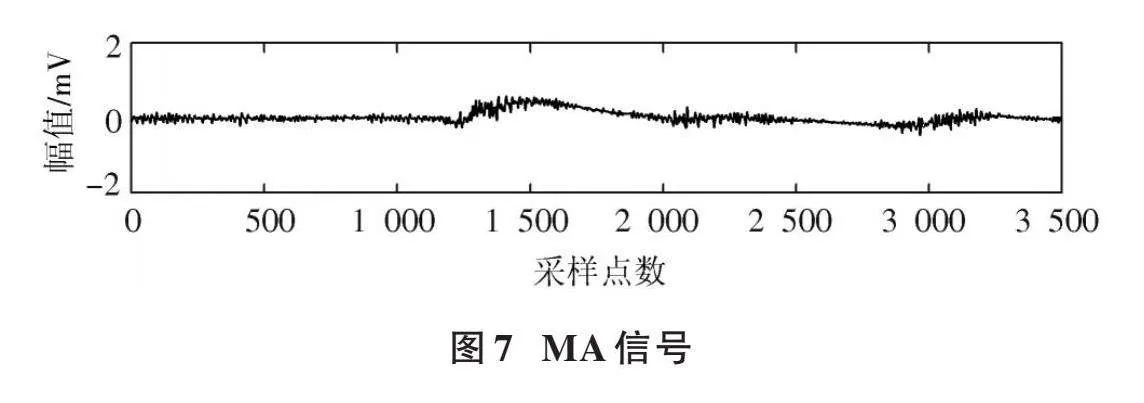
为了进一步验证本文方法在实际ECG上的去噪效果，选取“MIT⁃BIH Noise Stress Test Database”中的肌电干扰（MA信号）作为干扰信号进行去噪实验分析，将MA信号与ECG合成可得真实测量的含噪ECG。MA信号如图7所示。

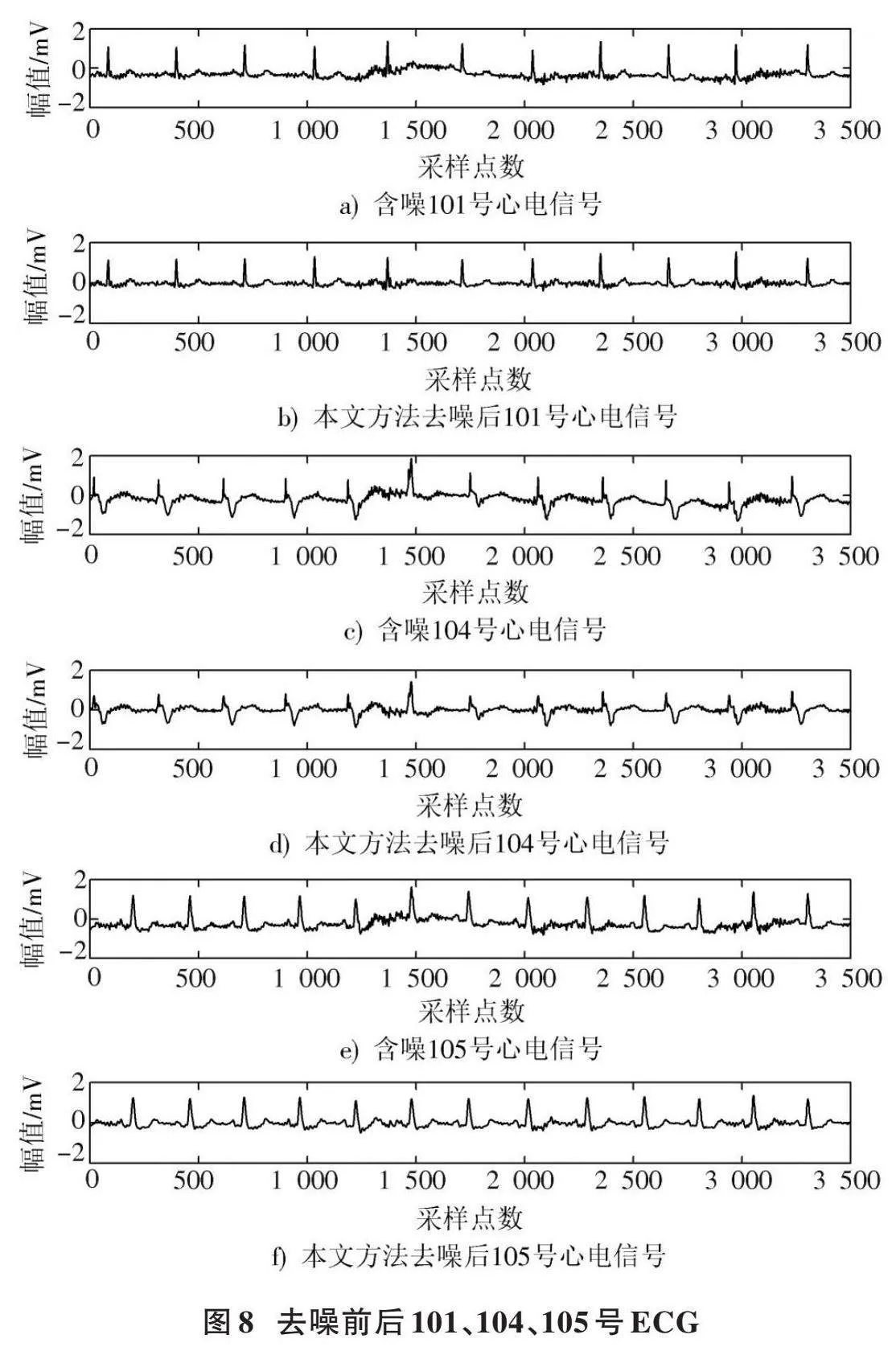
选取“MIT⁃BIH”心电数据库中正常ECG101号、105号和戴有起搏器患者的ECG104号，与MA信号结合形成真实测量的含肌电干扰的ECG信号，采用小波阈值去噪、EMD、EMD⁃小波阈值去噪、本文方法分别对含有MA的101号、104号、105号ECG进行去噪实验。含MA的101、104、105号ECG与本文方法重构后的101、104、105号ECG对比如图8所示。

由于原始ECG与MA均包含少量的基线漂移噪声，SNR与MSE评估的准确性受到严重影响，因此，在评估和验证实测ECG时，仅采用了去噪后的ECG与原始ECG之间的自相关系数（AC）进行评估。不同ECG去噪后ACF值如表2所示。

由表2可知，与其他去噪方法相比，采用本文提出的去噪方法得到的AC值最接近1，表明经本文方法去噪后得到的ECG与原始ECG相似度最高，更大程度地保留了原始ECG的信号特征。

5" 结" 论

本文针对心电信号中的肌电干扰去除问题，提出一种参数优化变分模态分解的信号去噪方法。为实现变分模态分解中分解层数K与惩罚因子α的自适应选取，提出了一种改进白鲸优化算法，通过设计动态边界条件和反向种群生成方式，提高了VMD参数自寻优的搜索能力；基于分解层数K与惩罚因子α对信号进行分解，利用相关系数筛选噪声主导模态，对噪声主导模态分量进行小波阈值去噪；将去噪后噪声分量与其余分量重构，实现信号去噪。

设计仿真与含真实肌电干扰的心电信号实验，将本文方法与EMD、小波阈值去噪、EMD⁃小波阈值去噪进行对比，采用信噪比、均方误差与自相关系数三个评价指标定量证明了本文方法的去噪效果优于其余三种方法。综上证明了本文方法在心电信号降噪中具有良好的降噪效果，是一种有效的去噪方法。

注：本文通讯作者为李新娥。

参考文献

[1] 陈倩蓉，梁永波，赵飞骏，等.基于心电⁃脉搏波的心血管疾病识别研究[J].中国医学物理学杂志，2019，36（2）：210⁃214.

[2] ASHISH K， HARSHIT T， VIRENDER K M， et al. Stationary wavelet transform based ECG signal denoising method [J]. ISA transactions， 2021， 144： 251⁃262.

[3] 徐晗昕，俞斌杰，柳丽，等.改进小波阈值函数在手部姿态获取中的应用[J].传感器与微系统，2023，42（11）：165⁃168.

[4] 杨承金，聂春燕，王慧宇，等.基于小波改进阈值的肌电干扰降噪研究与效果评估[J].电子测量技术，2021，44（22）：80⁃86.

[5] SINGH B N， TIWARI A K. Optimal selection of wavelet basis function applied to ECG signal denoising [J]. Digital signal processing， 2006， 16（3）： 275⁃287.

[6] 施佳朋，黄汉明，薛思敏，等.基于EMD⁃VMD⁃LSTM的地震信号分类研究[J].传感器与微系统，2021，40（6）：57⁃59.

[7] 朝乐蒙，梁莹，夏慧琳.基于经验模态分解联合小波阈值的自适应心电信号基线漂移噪声去除[C]//中国医学装备大会暨2021医学装备展览会论文汇编.苏州：《中国医学装备》杂志社，2021：108⁃114.

[8] 卢莉蓉，牛晓东，王鉴，等.基于EMD与IMF分量统计特性的ECG去噪[J].中国医学物理学杂志，2021，38（12）：1529⁃1534.

[9] 蔡改贫，李波波，赵鑫，等.基于自适应VMD⁃Hilbert的球磨机负荷参数预测[J].传感器与微系统，2023，42（9）：133⁃136.

[10] 卢莉蓉，王鉴，牛晓东.基于VMD和小波阈值的ECG肌电干扰去噪处理[J].传感技术学报，2020，33（6）：867⁃873.

[11] ZHANG M， JIANG Z， FENG K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump [J]. Mechanical systems and signal processing， 2017， 93： 460⁃493.

[12] 郁伟，李正权，邢松.改进WOA⁃VMD算法的心电信号去噪[J].中国医学物理学杂志，2023，40（9）：1143⁃1150.

[13] ZHONG C T， LI G， MENG Z. Beluga whale optimization： a novel nature⁃inspired metaheuristic algorithm [J]. Knowledge⁃based systems， 2022， 251： 109215.

[14] 杨承金，聂春燕，车敏诗，等.心电信号去噪效果的评估与分析[J].计算机工程与应用，2022，58（1）：300⁃312.

[15] 魏安凯，王娜，丁军航，等.基于优化SSA⁃VMD的滚动轴承故障信号降噪方法[J].电子设计工程，2024，32（16）：64⁃68.