几何世界的魅力

构成几何图形最基本的要素就是点，无数点排列组合就成了线。线又分为直线、射线、线段三种。直线没有端点，两端可以无限延长；射线有一个端点，另一端可以无限延长，我们平时看到的光束就是射线；线段有两个端点，我们可以测量其长度。点、线、面创造了我们的图形世界。

图形的分类

图形分为两种，分别为平面图形和立体图形。常见的平面图形有正方形、长方形、三角形、圆等。每种平面图形都有自己的特点，正方形的四条边长长度相等，长方形相对的两个长或宽长度相等，如果要组成一个三角形，则需要满足两边之和大于第三条边的条件。

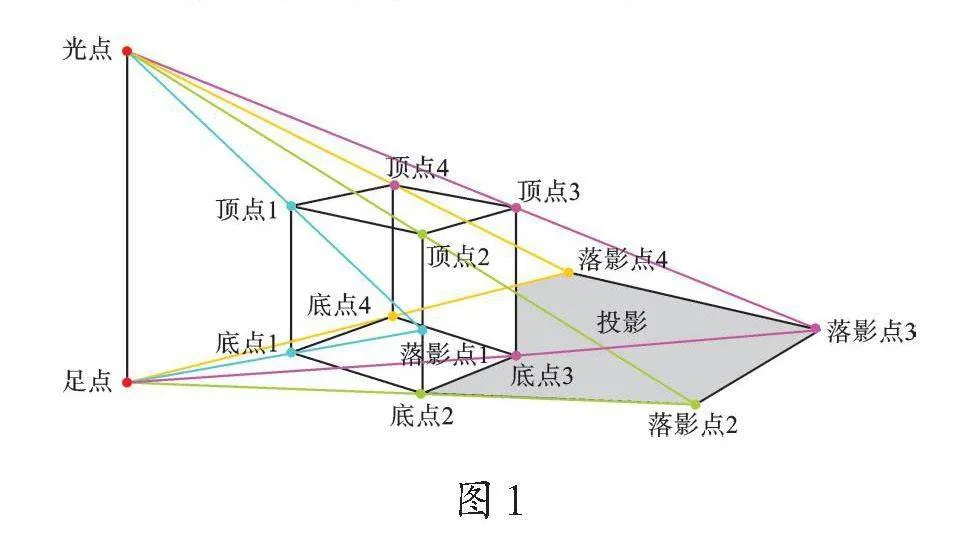
而立体图形就是将我们日常生活中看到的形状转移到了纸上。有趣的是，一束光照射在三维的立体图形上，其投影却成了二维的平面图形（如图1），这些图形又可以分为规则图形和不规则图形。

不规则图形的面积与体积计算

计算不规则图形的面积或体积，我们可以用切割或填补的方法。例如，我们在六年级常遇到的问题就可以用这一方法：一个长方体，如果高增加了3厘米就变成了一个正方体，这时表面积比原来增加了96平方厘米，问原来长方体的表面积是多少平方厘米，体积是多少立方厘米。

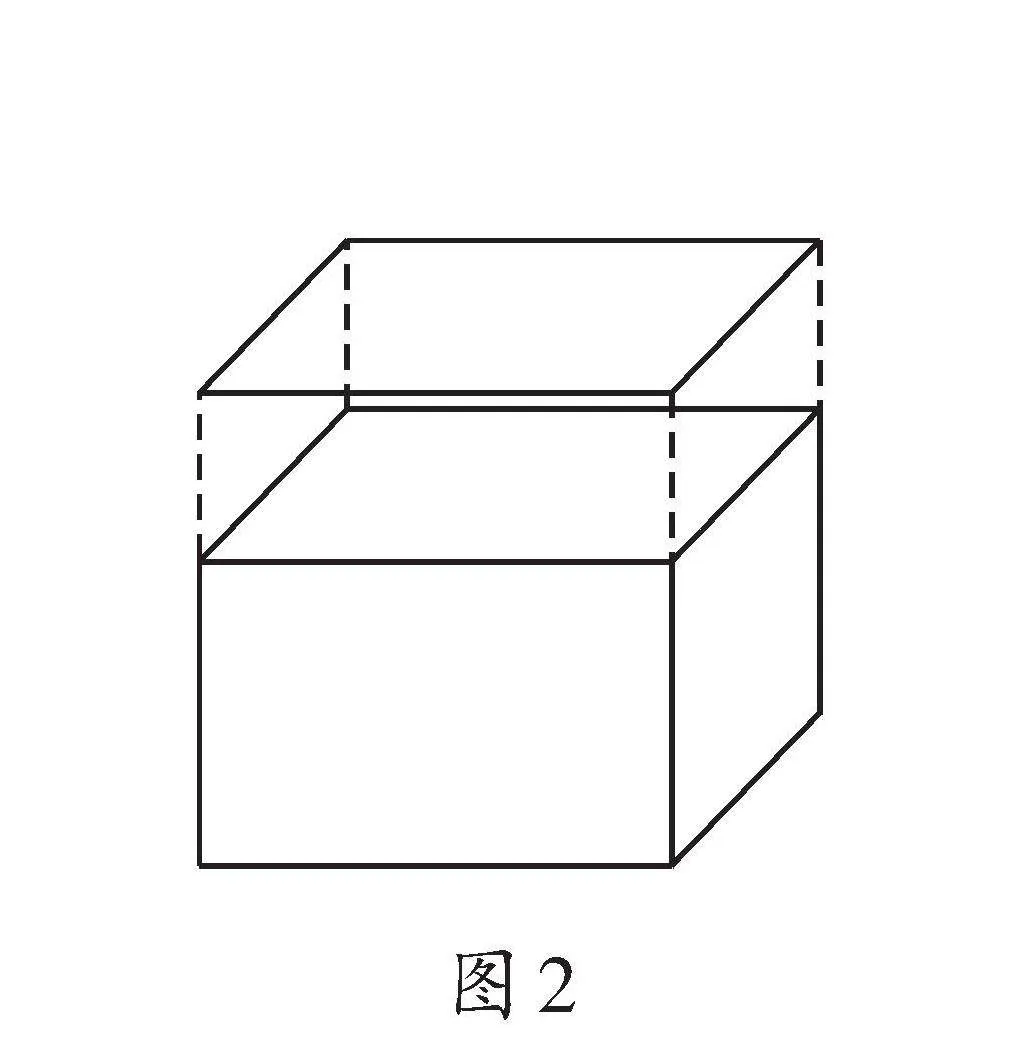
这时，我们可以绘制出图2，知道正方体六个面的面积相等，算出多出的一个面的面积为96÷4=24（平方厘米）。为什么除以4而不是除以5呢？因为上面的面，我们可以看成下面的长方体的顶面向上平移，所以除以4。由此得出一个面的面积是24平方厘米，再除以高增加的3厘米，可以得出正方体的边长为8厘米。我们知道正方体的六个面都是正方形，由此可以得出长方体的长和宽都为8厘米。而高未知，这时我们可以用正方体的边长减去增加的3厘米得出长方体的高为5厘米。现在我们知道了长方体的长、宽和高，那么长方体的表面积为两倍的长×宽加上四倍的长×高，得出结果为288平方厘米；而体积则为长×宽×高，得出结果为320立方厘米。

在我们的日常生活中，几何图形无处不在，它们构成了我们所居住的世界的基础。地球本身不是一个完美的球体，而是一个不规则的球体，这是几何学中的一个实例。数学家们在自然界中发现了许多引人入胜的模式和规律，这些发现不仅丰富了数学的内涵，也让我们能够用数学的视角来观察和理解周围的世界。

教师点评

小作者首先从构成几何图形的基本要素入手，为同学们介绍了几何图形的分类，又进一步建立数学模型，介绍了一种常用的求几何图形面积与体积的方法。小作者通过实例发现数学的美妙，体现出自身的创造力。几何图形千变万化，在各个领域均有广泛的应用，希望各位同学能像小作者一样感受到几何图形的魅力。

（指导教师：马宇歌）