一类非凸Bregman梯度法的线性收敛研究

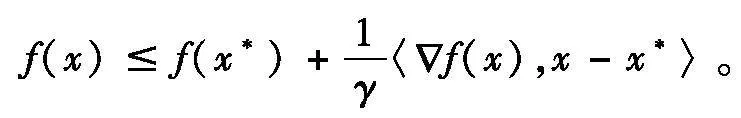
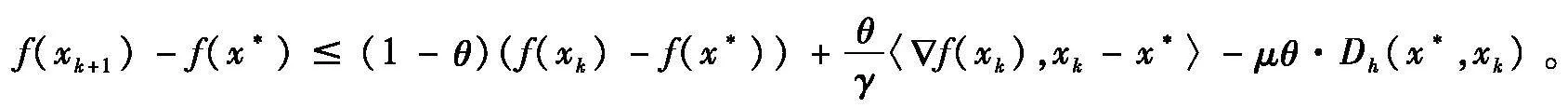
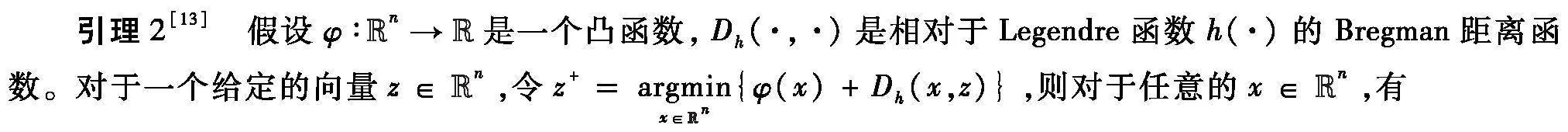
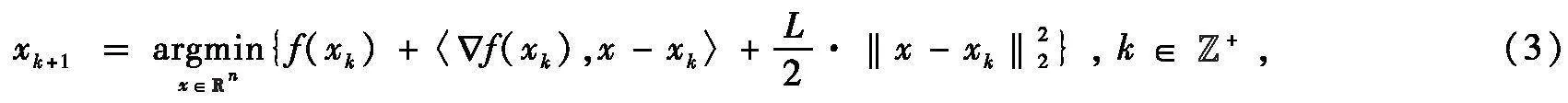
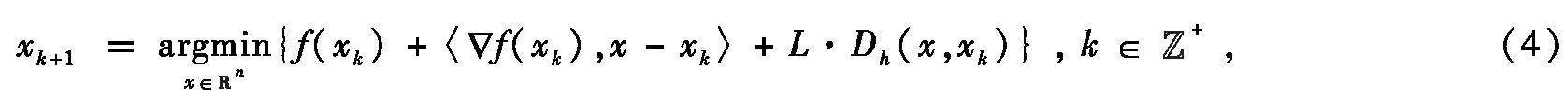
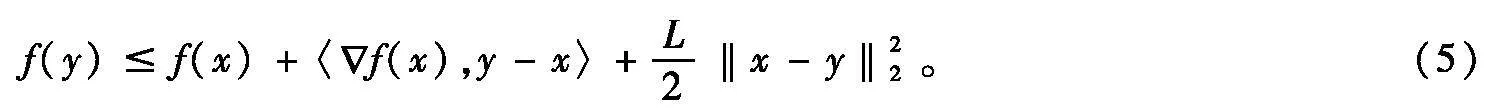
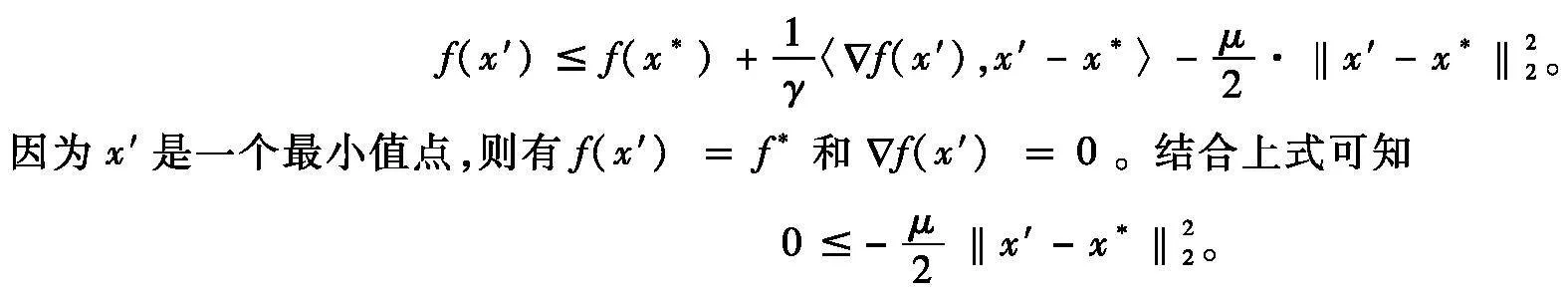
摘要：梯度下降算法是一类求解无约束优化问题的重要方法，其研究中光滑性的假设具有重要作用。Bregman梯度下降算法是对梯度下降算法的一种推广，本质上可以看作将经典的光滑性削弱成相对光滑性时自然产生的。文章研究了Bregman梯度下降算法求解相对强quasar-凸和相对光滑问题的线性收敛性，证明了当目标函数为相对强quasar-凸且相对光滑时，Bregman梯度下降算法产生的函数值序列具有线性收敛速度，同时，给出了迭代序列的收敛性。

关键词：相对光滑；强quasar-凸；相对强quasar-凸；Bregman梯度下降算法；线性收敛率

中图分类号：O224文献标志码：A文章编号：1673-5072（2025）01-0030-06

Linear Convergence of a Class of Non-convex Bregman Gradient Algorithm

Abstract：Gradient descent algorithm is an important method for solving unconstrained optimization problems，and the assumption of smoothness plays a crucial role in its research.Bregman gradient descent algorithm is" an extension of the gradient descent algorithm，and it can be essentially seen as a natural outgrowth when the classical smoothness is reduced to relative smoothness.This paper studies the linear convergence of Bregman gradient descent algorithm for solving relatively strongly quasar-convex and relatively smooth problems.It is proved that when the objective function is relatively strongly quasar-convex and relatively smooth，the sequence of function value produced by Bregman gradient descent algorithm has a linear convergence rate.Meanwhile，the convergence of iterative sequence is also given.

Keywords：relatively smooth;strongly quasar-convex;relatively strongly quasar-convex;Bregman gradient descent algorithm;linear convergence rate

本文考虑如下无约束优化问题

minx∈Rnf（x），（1）

式中，f ：Rn→R是一个可微函数。假设问题（1）的解集非空，并记为X*；其最优函数值用f*表示。求解问题（1）的方法有很多，当目标函数f为凸且L-光滑时，可利用经典梯度下降算法［1］进行求解，其迭代格式为

实际上，梯度下降算法（2）也可以看成去依次最小化f的二次逼近函数，即

式中，‖·‖2是欧式范数。算法（2）产生的迭代序列{xk}收敛到X*中一点，函数值序列{f（xk）}次线性收敛到f*［1］。当目标函数f为强凸且光滑时，可以得到算法（2）产生的函数值序列和迭代序列均具有线性收敛率［2］。因此，产生了如下疑问：如果将目标函数的凸性和光滑性至少削弱一个，能否得出与凸光滑函数类似的次线性收敛结论？如果将目标函数的强凸性和光滑性至少削弱一个，能否得出与强凸光滑函数类似的线性收敛结论？

首先，若将目标函数的凸性和光滑性至少削弱一个，能得出与凸光滑函数类似的次线性收敛结论。一方面，若将函数的凸性削弱为quasar-凸［3］，Guminov等［4］在2017年证明了在目标函数为quasar-凸且光滑时，梯度下降算法产生的函数值序列具有次线性收敛率。另一方面，若将函数的光滑性削弱为相对光滑性，类似光滑性导出梯度下降算法（3），相对光滑性的出现自然导出了Bregman梯度下降算法［5］（Nolips算法［6］或原始梯度算法［7］）：

式中，Dh（·，·）是由Legendre函数h（·）定义的Bregman距离函数。当目标函数为凸且相对光滑时，Bauschke等［6］得出算法（4）的收敛性和次线性收敛率；Lu等［7］得出算法（4）的次线性收敛率。实际上，若将目标函数的凸性和光滑性同时削弱，即当目标函数为quasar-凸且相对光滑时，算法（4）产生的函数值序列具有次线性收敛率。此外，若quasar-凸性参数γ1，还能得出迭代序列的收敛性。

另外，若将目标函数的强凸性和光滑性分别进行削弱时，也能得出与强凸光滑函数类似的线性收敛结论。一方面，若将强凸性削弱为强quasar-凸性，Bu和Mesbahi［8］得出当目标函数为强quasar-凸且光滑时，算法（2）产生的迭代序列和函数值序列均具有线性收敛率。另一方面，若将光滑性削弱为相对光滑性，Lu等［7］得出当目标函数为相对强凸且相对光滑时，算法（4）产生的函数值序列的线性收敛率。

综上所述，目前并没有关于将目标函数的强凸性和光滑性同时进行削弱时的线性收敛性方面的结果。因此，本文将探究当目标函数为相对强quasar-凸且相对光滑时，Bregman梯度下降算法的线性收敛性。

1预备知识

定义1［1］令Lgt;0，称可微函数f∶Rn→R是L-光滑的，如果对任意的x，y∈Rn，有

‖f（x）－f（y）‖2L·‖x－y‖2。

L-光滑条件可以得到下降引理：对于任意的x，y∈Rn，满足

尽管光滑性是优化中的一个重要性质，但在许多应用中，目标函数并不具有这样好的性质。2016年，Bauschke等［6］提出了Lipschitz-like凸性条件，该条件弱于光滑性但强于非光滑性，而后在2018年又被Lu等［7］独立地发现并将其重新命名为相对光滑条件。

下面将先回顾Legendre函数的定义。

给定一个Legendre函数h（·），则与h（·）相关的用作邻近测度的Bregman距离函数Dh（·，·）就被确定了［10］：

文献［7］给出如下相对光滑函数的例子。

quasar-凸性是一个重要的凸性推广条件。接下来，回顾一下quasar-凸性的定义。

定义5［3］假设x*是可微函数f ：Rn→R的一个最小值点。称f（·）关于点x*是γ-quasar-凸的，如果对于任意的x∈Rn，存在一个实数γgt;0使得

下面本文将给出2个quasar-凸函数的例子，可直接利用定义5进行证明。

与强凸函数类似，当μgt;0时，强quasar-凸函数也具有唯一的最优解。本文以引理的形式给出，并进行证明。

引理1如果函数f（·）关于点x*是（γ，μ）-强quasar-凸的且μgt;0，则它有唯一的最优解。

证明假设x′是函数f（·）的另一个最小值点。令不等式（6）中的x=x′，则有

该不等式成立当且仅当x′=x*，则与假设矛盾。

本质上，相对强quasar-凸函数的定义思想和相对光滑函数的定义思想一致，都是借助Bregman距离函数Dh（y，x）将函数推广到非欧几何空间。下面，根据Zhu和Guo［12］定义相对强凸函数的思想来类似地定义相对强quasar-凸函数。

定义7令h∶Rn→R∪{+}为Legendre函数，并假设x*是可微函数f ：Rn→R的一个最小值点。称f（·）在Rn上相对于h（·）关于点x*是（γ，μ）-强quasar-凸的，如果对于任意的x∈Rn，存在实数γgt;0，μ0使得

类似引理1，即（γ，μ）-强quasar-凸函数最优解唯一性的证明（μgt;0），－μ·Dh（x*，x′）0并不能说明x′=x*，因此，（γ，μ）-相对强quasar-凸函数不一定具有唯一的最优解。

2相对光滑相对强quasar-凸函数的线性收敛率

本节考虑问题（1），其中f（·）相对于Legendre函数h（·）是L-光滑的且相对于h（·）关于一个最小值点x*是（γ，μ）-强quasar-凸的函数（Lgt;μgt;0）。首先，分析函数值序列{f（xk）}和序列{Dh（x*，xk）}的线性收敛性。下面直接给出分析收敛性需要用到的一个关于Dh（·，·）的性质。

φ（x）+Dh（x，z）φ（z+）+Dh（z+，z）+Dh（x，z+）。

定理1假设f∶Rn→R在Rn上相对于Legendre函数h（·）是L-光滑的且相对于h（·）关于一个最小值点x*是（γ，μ）-强quasar-凸的函数，其中Lgt;μgt;0。令序列{xk}是由Bregman梯度下降算法（4）产生的迭代序列。则序列{f（xk）}线性收敛到f（x*），序列{Dh（x*，xk）}线性收敛到0。

证明由于f（·）相对于h（·）是L-光滑的，则对于任意的k∈Z+有

令上式中的x=x*，可得：

〈f（xk），xk－x*〉L·Dh（x*，xk）－L·Dh（x*，xk+1）+f（xk）－f（xk+1）。（11）

由于f（·）相对于h（·）关于x*是（γ，μ）-强quasar-凸的，即满足

取任意θ0，式（12）左右两边同时乘以θ，然后将得到的式子与式（10）相加，则

将上式与式（11）结合得到

整理上式得

因此，由上式递归得

3结语

参考文献：

［1］BECK A.First-order methods in optimization［M］.Philadelphia：SIAM，2017.

［2］NESTEROV Y.Introductory lectures on convex optimization：a basic course［M］.Boston：Kluwer Academic Publishers，2004.

［3］HARDT M，MA T，RECHT B.Gradient descent learns linear dynamical systems［J］.Journal of Machine Learning Research，2018，19（29）：1-44.

［4］GUMINOV S，GASNIKOV A，KURUZOV I.Accelerated methods for alpha-weakly-quasi-convex problems［J］.Computational Management Science，2023，20（1）：36.

［5］DRAGOMIR R A，TAYLOR A B，D’ASPREMONT A，et al.Optimal complexity and certification of Bregman first-order methods［J］.Mathematical Programming，2022，194：41-83.

［6］BAUSCHKE H H，BOLTE J，TEBOULLE M.A descent lemma beyond Lipschitz gradient continuity：first-order methods revisited and applications［J］.Mathematics of Operations Research，2017，42（2）：330-348.

［7］LU H H，FREUND R M，NESTEROV Y.Relatively smooth convex optimization by first-order methods，and applications［J］.SIAM Journal on Optimization，2018，28（1）：333-354.

［8］BU J J，MESBAHI M.A note on nesterov’s accelerated method in nonconvex optimization：a weak estimate sequence approach［Z/OL］.（2020-06-15）［2023-12-04］.https：//arxiv.org/abs/2006.08548.

［9］ROCKAFELLARR T.Convex analysis［M］.Princeton：Princeton University Press，1970.

［10］BREGMAN L M.The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming［J］.Ussr Computational Mathematics amp; Mathematical Physics，1967，7（3）：200-217.

［11］HINDER O，SIDFORD A，SOHONI N S.Near-optimal methods for minimizing star-convex function and beyond［J］.Conference on Learning Theory，2020：1042-1085.

［12］GUO K，ZHU C R.On the linear convergence of a Bregman proximal point algorithm［J］.Journal of Nonlinear and Variational Analysis，2022，6（2）：5-14.

［13］CHEN G，TEBOULLE M.Convergence analysis of a proximal-like minimization algorithm using Bregman functions［J］.SIAM Journal on Optimization，1993，3（3）：538-543.