基于k-center聚类和最近邻中心的公平数据汇总

摘要：公平数据汇总是指从每种数据类别中选择有代表性的子集，且满足公平性要求。在大数据时代，每种类别的数据都是海量的，因此公平数据汇总研究具有非常重要的现实意义。为了使公平数据汇总的数据点更具有代表性，提出了基于k-center聚类和最近邻中心的公平数据汇总算法。算法主要包括2个基本步骤：（1）通过k-center聚类，将k个簇中心作为当前汇总结果；（2）选择满足公平约束的原簇中心的最近邻点作为新簇中心。由于更新簇中心时选择的是原簇中心的最近邻点，因此相对随机选择的数据点，最近邻点更具有代表性，是除原始簇中心外的次优代表点。同时，寻找最近邻点作为新的簇中心能最大限度减少公平代价。在2个模拟数据集和6个UCI真实数据集上的对比实验结果表明，所提出的算法在近似因子和公平代价方面都优于对比算法，说明所提出的算法获得的数据汇总更具有代表性。

关键词：最近邻点；k-center聚类；数据汇总；公平约束

中图分类号：TP311.1文献标志码：A文章编号：1673-5072（2025）01-0095-09

Fair Data SummarizationBased on k-Center Clustering and Nearest Neighbor Center

Abstract：The fair data summarization refers to selecting representative subset from each data category and satisfying the fairness requirement.In the era of big data，each category may contain a large volume of data，so the research into fair data summarization is of great practical importance.To enhance the representativeness of data points in data summarization，we proposed a fair data summarization algorithm based on k-center clustering and nearest neighbor center.The algorithm mainly consists of two basic steps：（1）" K centers are taken as the current summarization result via" k-center clustering；（2） The nearest neighbors of the original cluster centers that satisfy the fairness constraints are selected as the new cluster centers.Because nearest neighbors are selected as new cluster centers，they are more representative compared to data points selected randomly，and they are also suboptimal representative points besides the original cluster centers.Moreover，selecting nearest neighbor points as new cluster centers can minimize the fairness cost.The comparison results on 2 simulated datasets and 6 real UCI datasets show that the proposed algorithm outperforms the compared algorithm in terms of approximation factors and fair cost，indicating that the data summarization obtained by the proposed algorithm is more representative.

Keywords：the nearest neighbor point；k-center clustering；data summarization；fairness constraint

随着互联网技术和信息技术的高速发展，生产和生活中产生的大量数据都已经实现了数字化存储和传播。海量的数据可以划分成不同的类别，每个类别同样也包含大量的数据。在检索某个类别数据时，检索者只希望获得该类别具有代表性的数据，为了获得不同类别数据具有代表性的数据点，数据汇总技术应运而生。数据汇总就是在大数据集里找到一个能够近似代表整个数据集的子集，可以将簇中心集看作数据的一个汇总。研究者主要基于现有的计算机技术来进行数据汇总，Hesabi等［1］总结了常被用于数据汇总的方法，如：聚类、采样、压缩和直方图等。然而，因为数据集本身存在偏差，从而导致数据汇总结果存在偏见［2］，在某些属性上没有体现公平性，例如，Ali等［3］发现在Facebook上85%的超市收银员招聘广告是针对女性，74%出租车司机的职位是针对黑人男性；Cowgill［4］发现，在自动招聘系统中，有着相同工作能力但毕业于非精英大学的人获得工作的机会减少了12%；Kay等［5］发现，在谷歌中搜索图片的关键词为“CEO”时，在搜索结果中，男性的比例远高于实际生活中的比例。为消除返回结果中的不公平性，研究者们在机器学习算法中引入了公平性概念［6］。到目前为止，算法公平性主要分为：反分类公平性（Anti-classifcation）［7］、个体公平性（Individual Fairness）和群体公平性（Group Fairness）［8］。目前应用最广泛的是群体公平性，它基于DI（Disparate Impact）理论［9］，即任何受保护组中的数据对象都不应受到决策系统结果的不利影响［10］。Chierichetti等［11］应用DI理论给出了公平定义，每个受保护组在每个簇中的比例应该接近在整个数据集中的比例。这里受保护组也称敏感属性组，若敏感属性是性别，则有男性组和女性组两个敏感属性组。基于该公平定义，研究者们提出或改进了一系列公平算法［12-17］。其中，Schmidt等［12］和Rsner等［13］将文献［11］的公平定义推广到了多于两个敏感属性组的聚类问题中。Bera等［18］也将文献［11］的公平定义进行了推广，只要在完成聚类的簇中敏感属性组所占比例在指定的上下界范围内就认为结果是公平的。

2018年，Celis等［19］在数据汇总中引入了公平性概念，通过在DDP（Determinantal Point Processes）［20］中嵌入敏感属性的分布概率来实现公平数据汇总。考虑到有时在输出结果中，敏感属性组的比例应该与输入数据集中的比例相同，但有时为了逆转人们的刻板印象（例如认为CEO等职位都为男性），又要求在输出结果中敏感属性组比例要相等。Celis等［19］整合了以上两种情况，定义了一种新的公平约束，从不同敏感属性组中选择指定数量的数据点作为输出结果。2019年，Kleindessner等［21］将文献［19］的公平定义推广到了k-center聚类算法中，将公平k-center聚类获得的簇中心集视为一个公平数据汇总，将为不同敏感属性组指定的汇总点数量作为公平约束。2022年，Angelidakis等［22］推广了文献［19］的公平约束，规定不同敏感属性组的汇总点数量必须在指定上下界范围内。

但是上述算法在实现公平约束时，是通过随机的方式选择数据点作为新的簇中心，这种方式使得k-center聚类结果不是最优解，造成新的簇中心代表性不强。文献［21］的算法虽然在数据汇总结果中实现了公平性，但是却提高了公平代价。针对该问题，本研究对文献［21］的算法进行改进，提出了基于k-center聚类和最近邻中心的公平数据汇总算法，其主要改进思想是在实现公平约束时，选择更具代表性的点作为簇中心，即选择原簇中心周围满足公平约束的最近邻点作为新簇中心，这比随机选择获得的簇中心更具有代表性，同时能最大限度减少为了实现公平约束时的公平代价。

1公平数据汇总算法

1.1k-center聚类

设S是有限的数据集，d∶S×S→R0是S上的距离度量，k∈Ζ+给定的参数是簇中心，本文用欧氏距离来度量两个数据点之间的距离，因此d满足三角不等式。k-center聚类的代价函数如下：

式中，C0表示预先指定的初始中心，集Ci表示簇中心，Kleindessner等［21］通过改进Gonzalez等［23］提出的2-近似算法来解决该将k-center聚类应用到数据汇总中，在某些应用场景中预先指定部分能出现在汇总结果中的问题，具体内容如算法1所示。

算法1k-center聚类算法。

1.2基于k-center聚类和最近邻中心的公平数据汇总

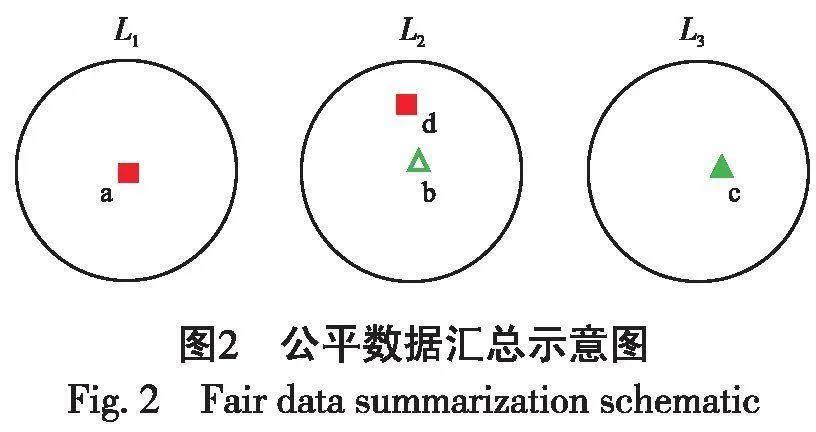
输出的簇中心集作为汇总点，而在公平数据汇总中要考虑敏感属性组之间的平衡，使得汇总结果是公平的，即输出的簇中心集在敏感属性上满足公平约束。图1和图2展示了两者之间的不同。假设本次公平数据汇总中规定2个敏感属性组的公平约束分别为2、1个。图1因为没有考虑敏感属性组，传统的数据汇总直接通过k-center聚类得到簇L1、L2、L3的簇中心分别是a、b、c。图2考虑到敏感属性组，在公平约束下得到的簇中心集合是a、d、c，其中d不是原来的簇中心。

k-center聚类是实现数据汇总的有效算法，该算法获得的簇中心都是簇内最具有代表性的点，但不一定满足公平性。在基于k-center聚类和最近邻中心的公平数据汇总中，为了满足公平性，在簇内选择数据点替换原来的簇中心时，满足公平约束条件的数据点可能不止一个。因为最近邻点是与簇中心点相似度最大或者距离最近的点，所以最近邻点是除簇中心外最能代表该簇的点。总之，为了满足公平性，选择簇中心的最近邻点替换簇中心，能够得到一个具有代表性的公平数据汇总。

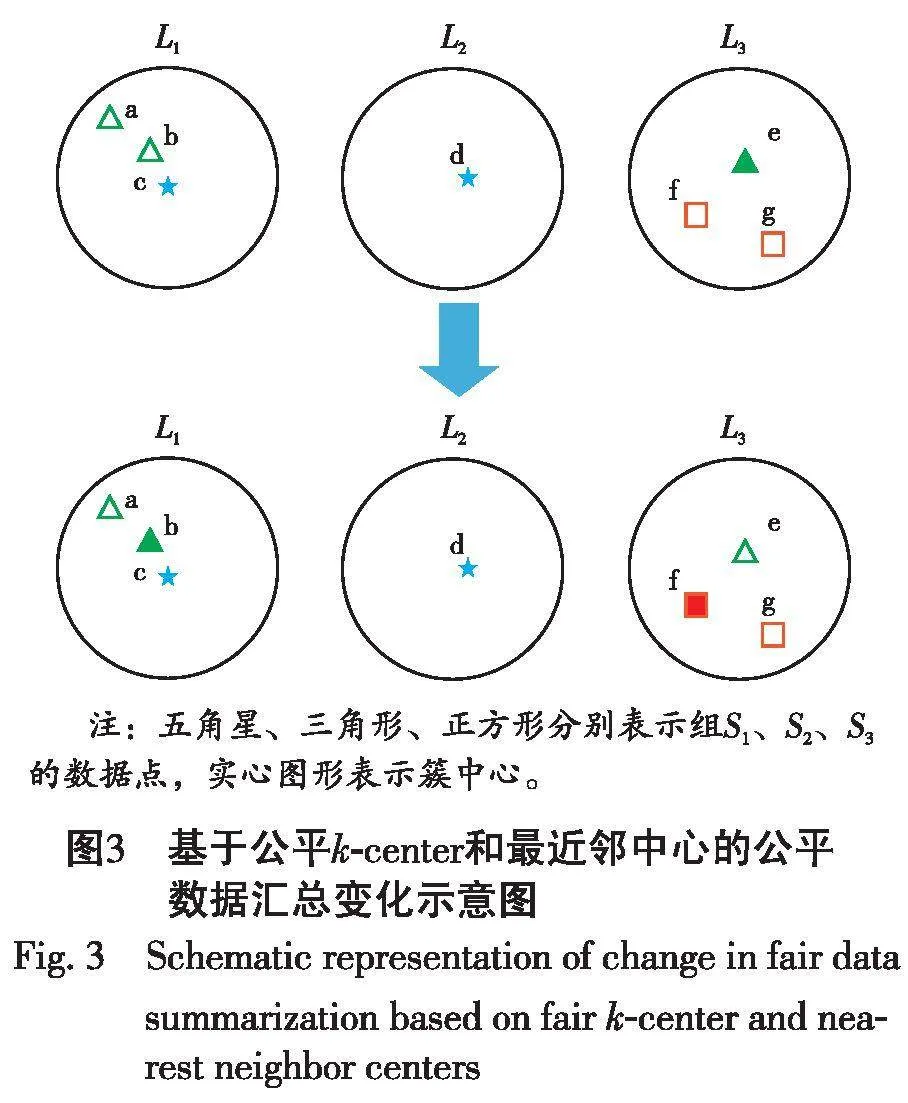
因此，利用最近邻来更新簇中心的主要思想可以概括为：运行算法1后，考虑仍然不满足公平约束的敏感组，其中一部分敏感组目前的簇中心数一定大于公平约束，一部分敏感组目前的簇中心数一定小于公平约束，这时就需要减少前者的簇中心数，增加后者的簇中心数。通过图3的方法，构造有向无权图G，找到图中簇中心数大于公平约束的敏感组到簇中心数小于公平约束的敏感组之间的最短路径，任选其中一条路径进行中

根据算法思想，最近邻中心算法的具体实现如算法2所示。

算法2最近邻中心算法。

S′中包含的敏感组数量少于m，对新数据集S′调用算法1，再调用算法2，每次调用都会减少S′中的敏感组数量，如此反复直到得到Γ为空，则完成整个数据集S的公平数据汇总操作。具体内容如算法3所示。

算法3基于k-center聚类和最近邻中心的公平数据汇总算法。

2实验与结果分析

2.1实验评价指标

为验证本文算法的有效性，分别在文献［21］设置的模拟数据集和UCI真实数据集上进行实验评估，并与文献［21］的算法进行比较。两个算法都设置相同的数据集和敏感属性组数量m，初始中心的个数|C0|，敏感属性组Si和对应的公平约束ki。

公平代价（Cost）是式（2）的收敛值。在满足公平约束的情况下，公平代价值越小，表示聚类效果越好，且选择的公平汇总点越具有代表性，反之，聚类效果越差，且公平汇总点代表性越差。近似因子（Approximation Factor）是式（2）收敛值与式（1）最优值的比值，其值大于等于1，越接近1表示收敛值越接近最优值，聚类效果好，且选择的公平汇总点越具有代表性。实验中能够计算得到模拟数据集的k-center聚类代价函数的最优解，所以选用近似因子衡量在模拟数据集上的数据汇总效果。而对于真实数据集，由于无法计算得到k-center聚类代价函数的最优解，因此采用公平代价衡量数据汇总效果。k-center聚类中，不同的初始点会导致最终聚类结果不一样，为了更完整地展示算法数据汇总性能，采用箱线图来展示，每组箱线图都包含了200次实验结果。为了表示方便，将本文的算法简称为NFK（Nearest Neighbor Fair k-center），文献［21］的算法简称为FK（Fair k-center）。

2.2模拟数据集上的近似因子对比

模拟数据集包括模拟数据集1和模拟数据集2。由于k-center聚类算法通过度量矩阵进行聚类，因此模拟数据集1通过ER随机图模型［24］模拟产生n个点的度量矩阵D以及每个点所属敏感属性组。度量矩阵中任意2个点之间的距离是0～100范围内均匀产生的随机数，点所属敏感属性组也是随机产生，即如果m个敏感属性组，那么对每个数据点随机产生1～m范围内的整数标记该点所属的组。

模拟数据集1只包含25个点，因此可以通过穷尽算法得到k-center聚类代价函数的最优值。实验中随机选择初始中心集C0，设置了不同m、|C0|、ki进行对比，进行了7组对比实验，具体设置为：

（1）m=2，|C0|=2，（k1，k2）=（2，2）；（2）m=2，|C0|=2，（k1，k2）=（4，2）；

（3）m=3，|C0|=2，（k1，k2，k3）=（2，2，2）；（4）m=3，|C0|=1，（k1，k2，k3）=（5，1，1）；

（5）m=4，|C0|=0，（k1，k2，k3，k4）=（2，2，2，2）；（6）m=4，|C0|=0，（k1，k2，k3，k4）=（3，3，1，1）；

（7）m=5，|C0|=0，（k1，k2，k3，k4，k5）=（2，2，2，1，1）。

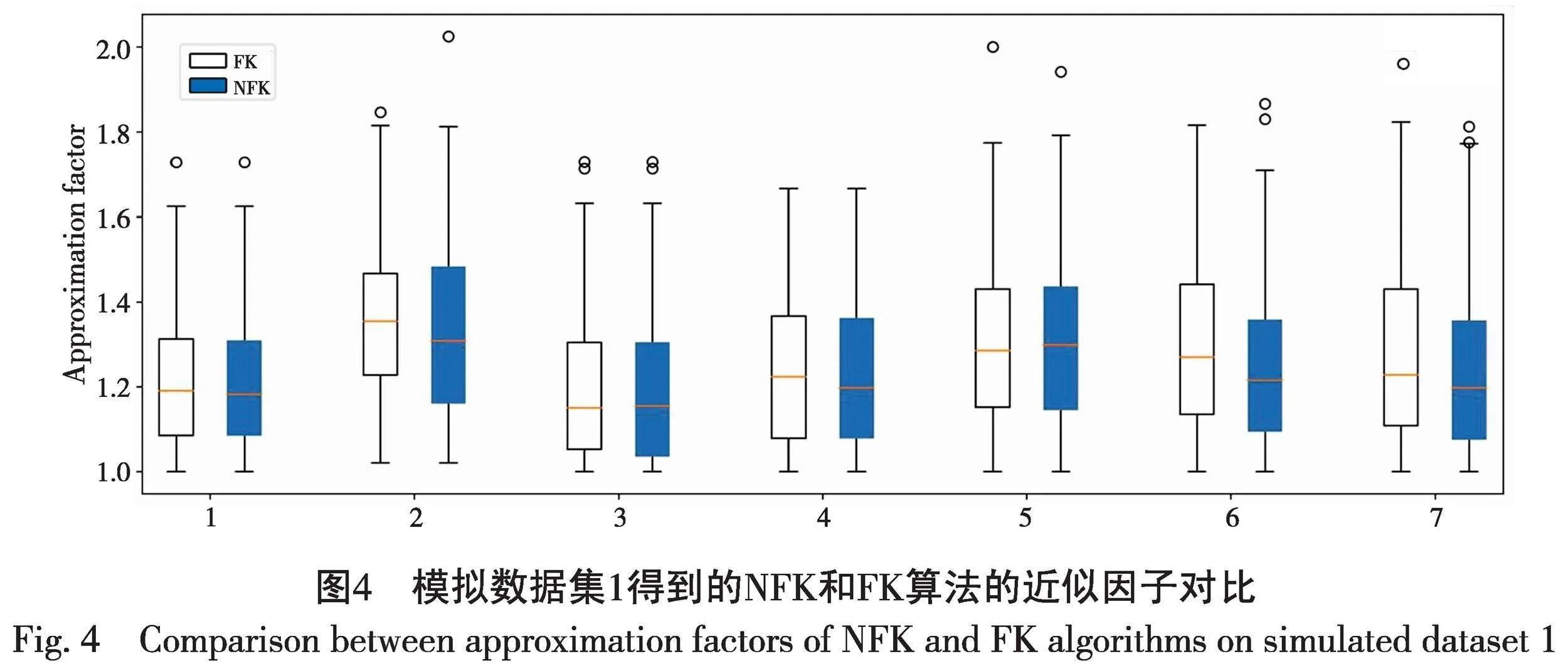
图4展示了NFK和FK算法在7组参数设置情况下的近似因子对比。从整体可以看出，两种算法得到的近似因子都比较低，极大值都小于2，中位数几乎都低于1.5，说明小数据集在满足公平约束的情况下，NFK算法和FK算法获得的公平数据汇总接近传统k-center聚类获得的最优数据汇总结果，说明两种算法选择的数据汇总点都比较接近聚类中心点，代表性比较强，两种算法在小数据集上都能找到较好的次优解。具体观察每组箱线图，第1组和3组中NFK和FK的极大值、中位数接近；第2组、4组、6组和7组表明NFK的中位数低于FK的中位数，但其中第2组和第4组中NFK和FK极大值接近，第6组和第7组NFK的极大值明显小于FK；第5组NFK的中位数、极大值略高于FK。这说明在小数据集上，NFK的数据汇总略好于FK，但不明显。

模拟数据集2包含10 100个点，属于大数据集，其产生方式为：首先指定100个簇中心点，（i，j）∈R2，i， j=0，…，9，在每个中心点周围0～0.5距离范围内均匀分布产生10 000个点，构成100个簇；然后将数据集中每个点随机分配给m个敏感属性组。实验时，随机选择第一个初始中心点作为初始中心集。由于每个簇中的点距离簇中心的最大距离为0.5，因此根据公式（1）可得k-center聚类代价函数的最优值为0.5。

图5展示了NFK和FK算法在不同m情况下的近似因子对比。从整体来看，将图4和图5的近似因子作比较，模拟数据集2实验得到近似因子比模拟数据集1的更大，其原因是随着数据量的增加，为了满足公平约束，越来越难以选择簇中心作为代表点，造成公平代价函数的值会增长很大。说明随着数据量的增加，获得有代表性的公平数据汇总越难。另外，从图5中可以看出，随着敏感属性组数量的增加，两种算法的近似因子都在非常缓慢增长，说明敏感属性组越多，获得有代表性的公平数据汇总也将越难。对比两种算法可以看出，NFK算法整体表现远远优于FK算法，NFK每一组的箱线图中极大值、上四分位数、中位数和下四分位数都明显低于FK，NFK算法的近似因子极大值不大于2.1，中位数近似于1.7，而FK算法中除第7组和15组外近似因子极大值都大于2.1，除第1组和2组外中位数近似于1.8。其原因在于NFK算法选择的公平汇总点比FK算法更接近k-center聚类的簇中心，从而获得更低的近似因子。说明在数据量更大时，NFK算法比FK算法更有优势，获得公平数据汇总点更具有代表性。

2.3真实数据集的公平代价对比

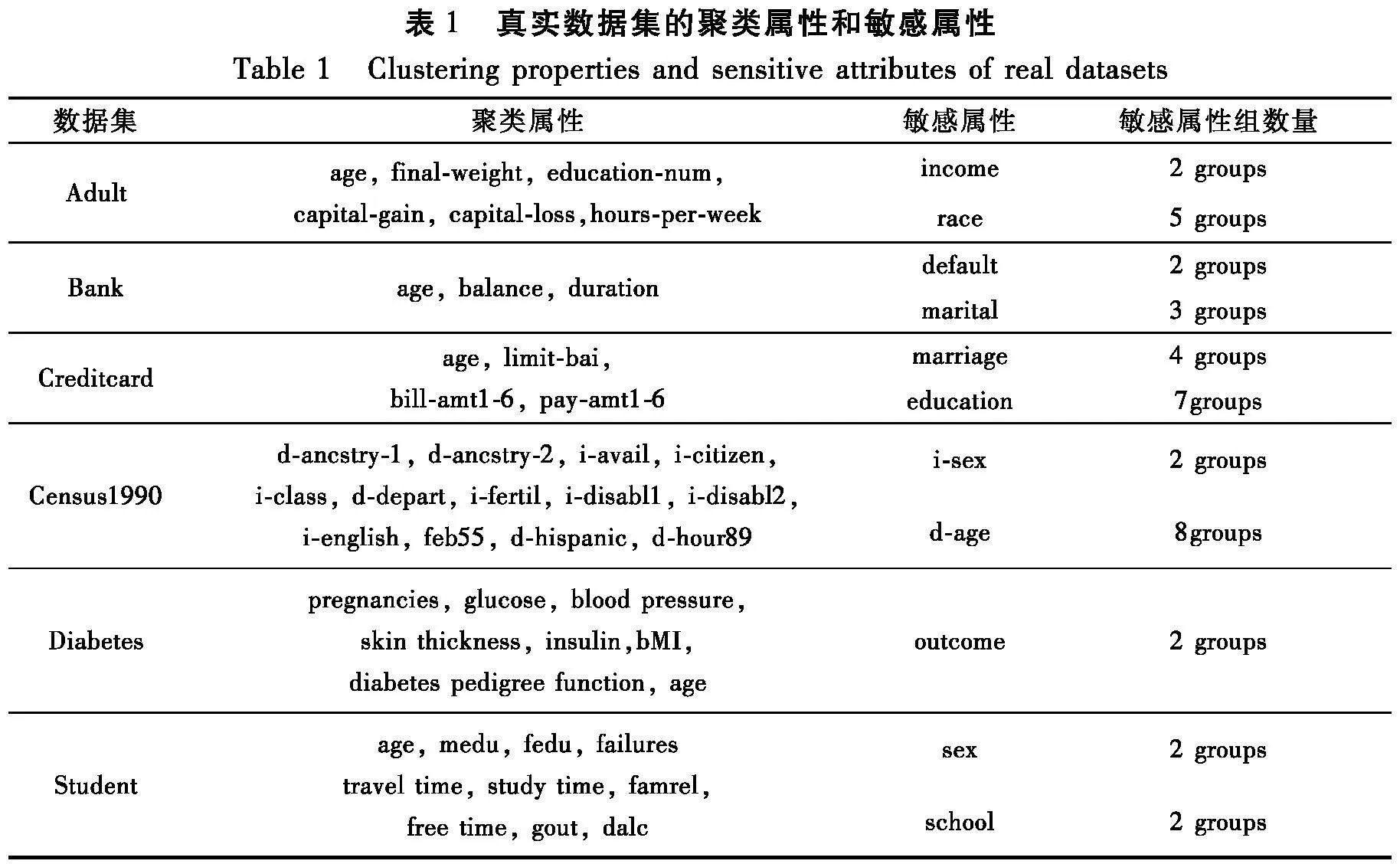
选取4个常被用于测试公平聚类算法的UCI真实数据集来测试本文算法。4个数据集分别是：（1）Adult数据集，包含25 000条1994年美国人口普查的相关数据；（2）Bank数据集，包含4000条葡萄牙某银行机构的电话营销活动相关数据；（3）Creditcard数据集，包含我国台湾省某信用卡30 000个持卡人的信息；（4）Census1990数据集，包含40 000条1990年美国人口普查的相关记录；（5） Diabetes数据集，包含768名皮马印第安人糖尿病数患者的信息，记录他们的血糖、血压、年龄、BMI和皮肤厚度等特征；（6） Student数据集，包含649条葡萄牙学生在中等教育阶段的成绩、人口统计、社会和学校相关属性。每个数据集的聚类属性和敏感属性如表1所示。

针对每个数据集进行4组实验，对每个真实数据集设置了不同的初始中心数|C0|和公平约束ki，i=1，…，m。

针对Adult数据集初始中心数|C0|都设置为100，其他参数设置分别为：（1）m=2，ki=50；（2）m=2，ki=170；（3）m=5，ki=20；（4）m=5，ki=140。

针对Bank数据集初始中心数|C0|都设置为10，其他参数设置分别为：（1）m=3，ki=10；（2）m=3，ki=70；（3）m=4，ki=10；（4）m=4，ki=70。

针对Creditcard数据集初始中心数|C0|都设置为100，其他参数设置分别为：（1）m=2，ki=20；（2）m=2，ki=170；（3）m=5，ki=30；（4）m=5，ki=110。

针对Census1990数据集初始中心数|C0|都设置为10，其他参数设置分别为：（1）m=2，ki=20；（2）m=2，ki=140；（3）m=8，ki=30；（4）m=8，ki=160。

针对Diabetes数据集初始中心数|C0|都设置为0，其他参数设置分别为：（1）m=2，ki=10；（2）m=2，ki=20；（3）m=2，ki=40；（4）m=2，ki=50。

针对Student数据集初始中心数|C0|都设置为0，其他参数设置分别为：（1）m=2，ki=10；（2）m=2，ki=20；（3）m=2，ki=15；（4）m=2，ki=30。

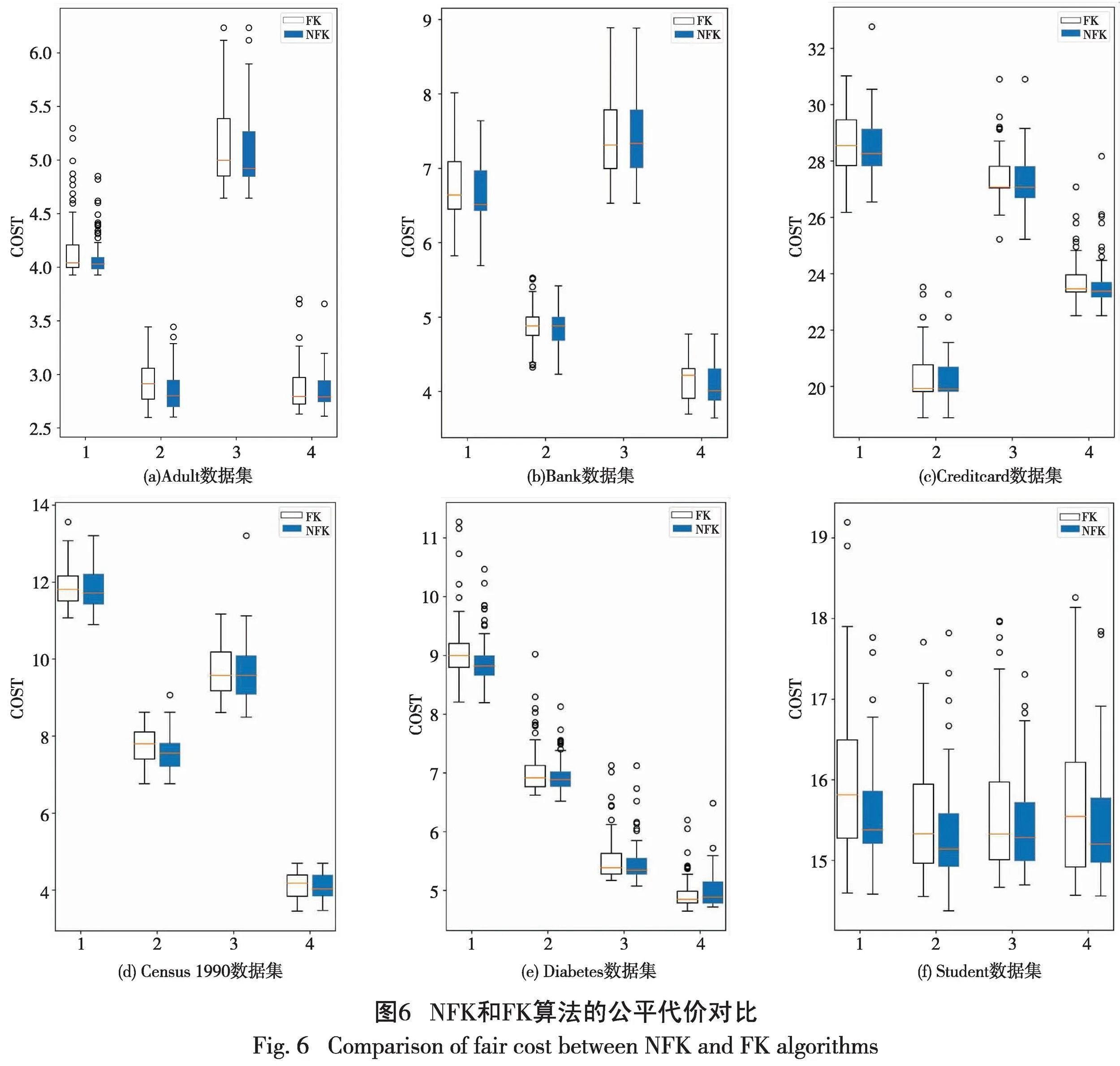
图6为NFK和FK算法在真实数据集上的公平代价对比。可以看出，无论在哪个数据集上，NFK算法的公平代价都优于FK算法。具体而言，NFK算法的箱线图盒体长度大多小于FK算法，说明NFK算法得到的实验结果波动程度比FK更小，NFK算法稳定性更强；NFK获得的每一组箱线图中的极大值、上四分位数、中位数大多数都低于FK，特别是在Adult、Bank和Student数据集上表现更明显，说明NFK选择的公平数据汇总点距离聚类中心近，更具有代表性。另外，两种算法在敏感属性组个相同的数情况下，每组选择的代表点数越多，其公平代价越小，这与公平代价计算公式1和2的意义是一致的。

3结束语

k-center聚类是实现公平数据汇总的有效算法，k-center聚类得到的簇中心集能够被视为原始数据集的一个汇总，是整个数据集具有代表性的子集。要获得公平的数据汇总，则需要替换部分簇中心，这将降低簇中心集汇总点的代表性。为解决该问题，本文提出了基于k-center聚类和最近邻中心的公平数据汇总算法，在更新策略中通过选择簇中心的最近邻点作为新簇中心，本算法能够为数据集生成一个更具代表性的公平数据汇总。在多个数据集的实验结果表明，NFK算法明显提高了公平数据汇总的代表性，有效降低了公平代价。由于NFK算法选择最近邻点比随机选择点需要耗费更多的计算时间，在进一步的研究中，如果数据集比较大时，可以考虑采用KD树搜索最近邻点从而提高计算速度。

参考文献：

［1］HESABI Z R，TARI Z，GOSCINSKI A，et al.Data summarization techniques for big data-a survey［M］//Handbook on Data Centers.Berlin，German：Springer，2015 （7）：1109-1152.

［2］MEHRABI N，MORSTATTER F，SAXENA N，et al.A survey on bias and fairness in machine learning［J］.ACM Computing Surveys，2021，54（6）：1-35.

［3］ALI M，SAPIEZYNSKI P，BOGEN M，et al.Discrimination through optimization：how Facebook’s Ad delivery can lead to biased outcomes［C］// Proceedings of the ACM on human-computer interaction.New York：ACM，2019：1-30.

［4］COWGILL B.Bias and productivity in humans and algorithms：theory and evidence from resume screening ［EB/OL］.（2020-03-21）［2023-07-03］.https：//api.semanticscholar.org/CorpusID：209431458.

［5］KAY M，MATUSZEK C，MUNSON S A.Unequal representation and gender stereotypes in image search results for occupations［C］// Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems.New York：ACM ，2015：3819-3828.

［6］DWORK C，HARDT M，PITASSI T，et al.Fairness through awareness［C］// Proceedings of the 3rd Innovations in Theoretical Computer Science Conference.Cambridge，Massachusetts：Association for Computing Machinery，2012：214-226.

［7］张贵红，邓克涛.社会化研究框架下算法公平性的实现策略研究［J］.科学学研究：2024，42（2）：248-255.

［8］TSAMADOS A，AGGARWAL N，COWLS J，et al.The ethics of algorithms：key problems and solutions［J］.Ethics，Governance，and Policies in Artificial Intelligence，2021（144）：97-123.

［9］FELDMAN M，FRIEDLER S A，MOELLER J，et al.Certifying and removing disparate impact［C］// Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York：ACM，2015：259-268.

［10］徐夏.公平聚类算法研究［D］.绵阳：西南科技大学，2022.

［11］CHIERICHETTI F，KUMAR R，LATTANZI S，et al.Fair clustering through fairlets ［C］// Proceedings of the 31st International Conference on Neural Information Processing Systems.Long Beach，California，USA：Curran Associates Inc.2017：5036-5044.

［12］SCHMIDT M，SCHWIEGELSHOHN C，SOHLER C.Fair coresets and streaming algorithms for fair k-means［C］// Approximation and Online Algorithms：17th International Workshop.Berlin，Germany：Springer，2020：232-251.

［13］RSNER C，SCHMIDT M.Privacy preserving clustering with constraints ［C］// 45th International Colloquium on Automata，Languages，and Programming （ICALP 2018）.Germany：Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik，2018：96：1-96：14.

［14］CHEN X，FAIN B，LYU L，et al.Proportionally fair clustering［C］// Proceedings of the 36th International Conference on Machine Learning.New York：Curran Associates，2019：1032-1041.

［15］AHMADIAN S，EPASTO A，KUMAR R，et al.Fair correlation clustering［C］// International Conference on Artificial Intelligence and Statistics.New York：PMLR，2020：4195-4205.

［16］JONES M，NGUYEN H，NGUYEN T.Fair k-centers via maximum matching［C］// Proceedings of the 37th International Conference on Machine Learning.New York：ACM，2020：4940-4949.

［17］徐夏，张晖，杨春明，等.公平谱聚类方法用于提高簇的公平性［J］.计算机科学，2023，50（2）：158-165.

［18］BERA S，CHAKRABARTY D，FLORES N，et al.Fair algorithms for clustering ［C］// Proceedings of the 33rd International Conference on Neural Information Processing Systems.New York：Curran Associates Inc，2019：4954-4965.

［19］CELIS E，KESWANI V，STRASZAK D，et al.Fair and diverse DPP-based data summarization［C］// International Conference on Machine Learning.New York：ACM，2018：716-725.

［20］KULESZA A，TASKAR B.k-DPPs：fixed-size determinantal point processes［C］// Proceedings of the 28th International Conference on Machine Learning （ICML-11）.New York：ACM，2011：1193-1200.

［21］KLEINDESSNER M，AWASTHI P，MORGENSTERN J.Fair k-center clustering for data summarization［C］ // Proceedings of the 36th International Conference on Machine Learning.New York：ACM，2019：3448-3457.

［22］ANGELIDAKIS H，KURPISZ A，SERING L，et al.Fair and Fast k-Center Clustering for Data summarization［C］// International Conference on Machine Learning.New York：ACM，2022：669-702.

［23］GONZALEZ T F.Clustering to minimize the maximum intercluster distance［J］.Theoretical Computer Science，1985，38：293-306.

［24］HASTIE T，TIBSHIRANI R，FRIEDMAN J H，et al.The elements of statistical learning：data mining，inference，and prediction［M］.New York：Springer，2009.