基于多参考点评价方法的高校研究生招生指标分配问题研究

摘要：近些年，基于多个单一教学和科研上的指标信息，各高校研究生院都在积极寻求构建合适的综合指标，解决当前高校面临的研究生招生指标合理分配问题。但是传统的加权求和方法，即计算弱综合指数，无法充分反映变量间的均衡性。为此，我们拟采用基于弱和强复合指标的多参考点评价方法来提高评估的客观性。其中，强综合指数是通过取合成指标的最小值而非加权求和来计算的，进一步将弱和强复合指标的混合加权和作为综合指标，既能考虑被评价者的平均得分，又能兼顾水平的均衡性。

关键词：弱综合指标；强综合指标；动态分配；MRP-WSCI方法

中图分类号：D9"文献标识码：Adoi：10.19311/j.cnki.16723198.2025.01.061

1"介绍

综合评价问题，诸如公司的绩效评价、高校的综合排名评价以及学生的综合素质评价等，是实际工作中常遇到的棘手问题。如何实现公平、合理的评价，一直是近年来研究的热点。这不仅关乎评价结果的准确性，更直接关系到各方利益的公平分配和社会秩序的和谐稳定。因此，研究如何构建科学、合理的综合评价体系，以及如何确保评价过程的公正性，具有重要的理论意义和实践价值。"本文重点探讨当前高校面临的研究生招生指标动态分配问题，本质上是高校研究生培养质量的评价问题。

王润东（2023）深入探讨了当前高校研究生招生指标分配模式的现状。他通过对相关指标进行权重赋予，并采用传统的加权平均计算方法，对弱综合指标进行计算，得出了指标分配的具体结果，并揭示了高校研究生招生指标分配方法的应然状态，为高校招生工作提供了理论支撑。陈一凡（2017）结合多所高校现行的研究生招生指标分配方案，深入剖析并总结出高校研究生招生指标分配的具体细则与问题。并对我国现存的研究生招生指标分配模型进行了分析与验证，总结出高校研究生招生指标分配所面临的困境及其原因。杨雁等（2009）在我国研究生招生指标分配领域，系统地梳理了现阶段的相关文献，基于深入研究，构建了一个两阶段的研究生招生指标体系。这一体系综合考量了上一年度招生工作，并结合当前的招生现状并适应不同高校和学科间的差异，建立了相应的研究生招生指标动态调整分配模型，确保招生工作更加公平、高效。针对高校研究生招生指标的分配问题，还有一些其他的参考文献可见文献。

但是，这些文献大多基于弱综合指数进行评价打分，只使用该指标不能体现出变量间的均衡性。为解决该问题，Ruiz等（2021）以及Ruiz和Gibari（2020）在提出了完全补偿即强综合指数的基础上，建议利用弱和强复合指标的多参考点评价方法（MRP-WSCI）来对感兴趣的问题进行综合性评价。文章第二部分简要回顾一下MRP-WSCI方法，第三部分将其应用到某高校研究生招生指标动态分配问题上，第四部分进行了简要总结。

2"MRP-WSCI方法概述

假设有J个单位需要评价，评价指标的个数为I个。xij表示单位j的指标i的评价值。假设我们使用层次分析法、主成分分析法等给出了权重μ1，μ2，…μn，各参考点强弱复合指标的构建步骤如下。

2.1"参考水平和共同尺度

对每一个指标i=1，…，I，假设决策者可以给出n个参考水平：q1i，q2i，…qni，它以某种方式定义了指标I的绩效水平（例如：非常差，差，一般，好，非常好），分别用q0i和qn+1i表示指标i可以取到的最小值和最大值。假设（n+2）维列向量qi=（q0i，q1i，…qni，qn+1i）T表示指标i的参考向量，给出参考水平后，将所有指标降至一个共同的尺度αt（t=0，…，n+1）（通常为由决策者或者分析师设置的默认值）。

2.2"成就函数

将每个指标xij转换成阈值αt（t=0，…，n+1）定义的尺度，定义如下的成就函数：

sij=si（xij，qi）=αt1+αtαt1qtiqt1i（xijqt1i），xij∈［qt1i，qti］，（t=1，…n+1）

其中，sij∈［αt1，αt］。

2.3"弱综合指标

允许单个指标之间进行补偿。即给定指标的不良表现可以通过另一个指标的良好表现来补偿。我们对权重μi进行归一化，使权重之和为1。即：

μwi=μi∑ik=1μk

利用归一化后的权重和成就函数，使用简单的加性加权聚合构造的弱复合指标：

WCIj=∑Ii=1μwisi（xij，qi）

2.4"强综合指标

强综合指标不允许任何补偿。使用不同的权值归一化，使最大的权值为1：

μsi=μimaxk=1，…，I{μk}

利用这些权重，修正后的成就标量化函数：

s-ij=si（xij，qi）=αt+（si（xij，qi）αt）μsi"si（xij，qi）∈［αt1，αt］"（t=1，…，n+1）

由此可得强综合指标：

SCIj=mini=1，…Isi-（xij，qi）

2.5"部分补偿

混合综合指标。可针对不同补偿程度构建中间（混合）复合指标（MCI）即：用λ表示补偿度，λ∈0，1

定义单位j对应的MCI为：MCIj=λWCIj+（1－λ）SCIj

其中，λ=0表示没有补偿（退化为强综合指标的值），λ=1表示完全补偿（退化为弱综合指标的值）

3"案例研究

我们收集了某高校研究生培养质量的部分数据，包括x1（各学院招生人数）、x2（研究生录取/计划率）、x3（学硕/专硕率）、x4（一志愿报录比）、x5（一志愿上线率）、x6（本校录取占比）、x7（研究生导师数）、x8（师生比）、x9（近三年优秀论文数）、x10（计划下达完成情况）。

3.1"相关权重的计算

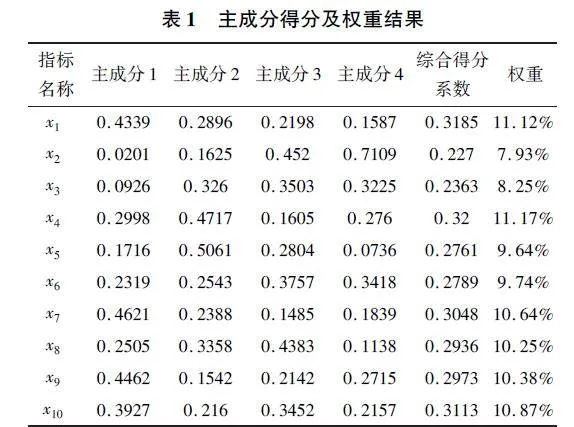
为了相对客观的给出权重，本文采用主成分分析法。首先对数据进行标准化处理，以消除量纲的影响，确保数据在同一水平线上。随后，进行主成分分析，得到解释的总方差、特征根、成分矩阵以及各指标对应的得分。相关结果见表1。

3.2"研究生数据MRP-WSCI综合指标

3.2.1"参考水平

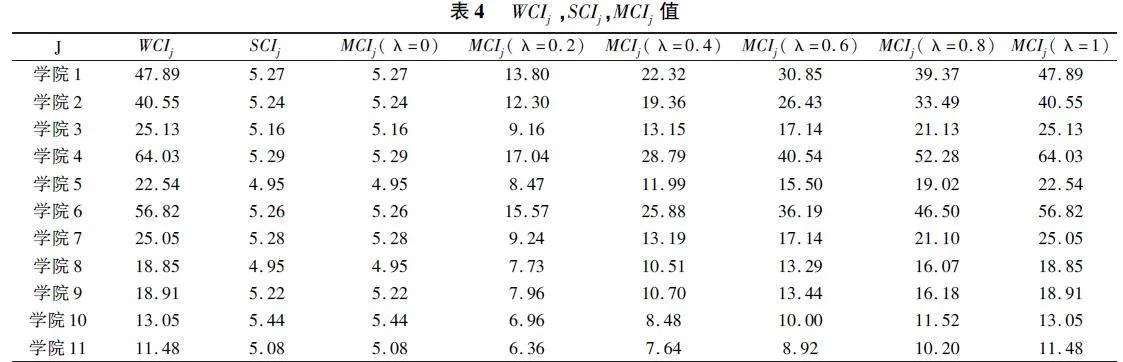
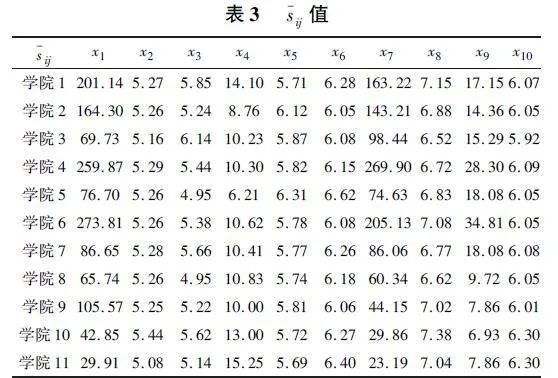
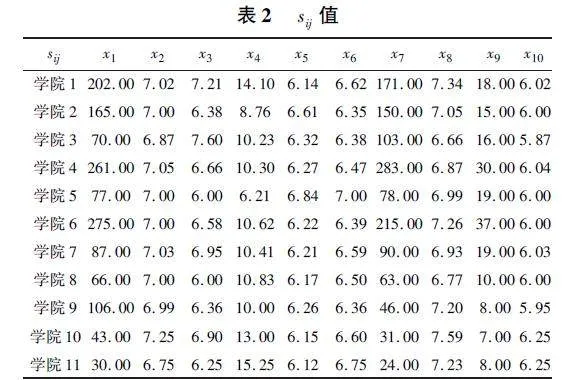
为了计算相关数据的WCI和SCI以及MCI，我们需要确定相关参考水平qi值以及αt值的对应值来定义相关的成就函数，采取的权重取自于主成分分析法最终得出的权重值，并以此来确定研究生10个指标的重要程度排序，统计出的指标排序后需要给出相应的qi值以及αt值，根据文献[8]和[9]，q的取值范围为[-6，6]（不包含0），α的取值范围为[1，10]。依据文献Ruiz等（2021）"[1]所提出的成就函数公式，初步计算出相应的sij见表2以及sij-见表3值，见下表2（其中J表示我高校的学院类别）：

3.2.2"强、弱综合指标

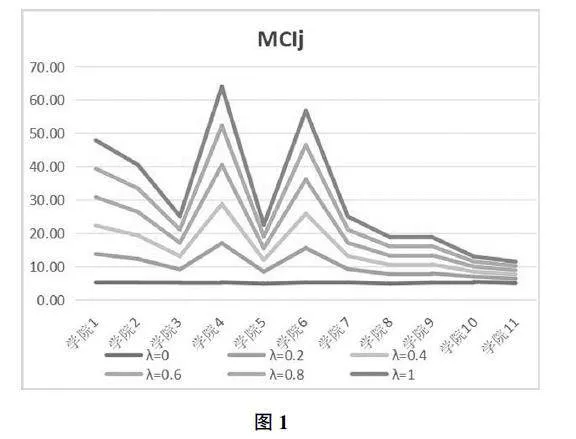
我们将主成分算出的权重带入P值以及α值，得到所有学院的WCI值。进一步，将权重标准化，再次带入P值以及α值得到所有学院的SCI值。最后，在不同的补偿程度（λ）下计算相应的MRP-WSCI综合指标系数。计算结果见表4。

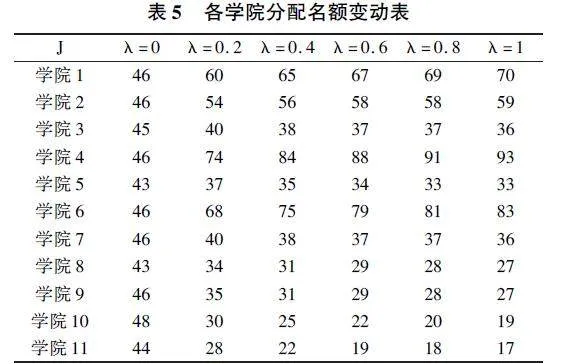
现在假定学校研究生招生办有500个名额需要进行动态分配，根据计算后的MRP-WSCI综合指标系数，对名额进行分配，结果见表5。通过表5，可以观察到随着补偿程度（λ）在（0，1）之间的变化，各个学院MRP-WSCI综合指标系数的等级是不同的，分配到的名额也会有所不同，且分配结果处于零补偿与完全补偿之间。此外，当λ在[0.6，0.8]时，可以观察到各学院的分配名额的变化较小，在没有先验信息、比如专家的建议的前提可以作为λ的适当取值范围。

4"总结

本文回顾了MRP-WSCI综合指标的计算方法，并利用其分析了某校研究生招生动态指标分配问题。结果显示，当λ在[0.6，0.8]时，各学院的分配名额的变化较小，在没有先验信息、比如专家的建议等的前提可以作为λ的适当取值范围。和只采用弱综合指数（λ=0）或者强综合指数（λ=1）两种极端情况相比，结果更加合理、公平。

参考文献

［1］王润东.高校硕士研究生招生指标分配制度改革研究[D].武汉理工大学，2023.

[2]陈一凡.高校内部研究生招生指标资源配置研究[D].华中农业大学，2018.

[3]杨雁，刘敏，李丹，等.基于学科建设和绩效考核的硕士研究生招生计划动态调整研究[J].黑龙江高教研究，2022，40（03）：8186.

[4]肖平，罗琼.质量视野下高校硕士研究生招生计划分配模型构建[J].教育教学论坛，2017，17：4142.

[5]王森林，樊传浩.研究生招生计划动态调整指标探析[J].文教资料，2021，（05）：12112273.

[6]张欣.面向“双一流”建设的研究生招生改革实践探讨——以华中农业大学园艺林学学院为例[J].大学教育，2022，（05）：249251.

[7]张勇强，徐寄尘，吴丹，等.高校硕士研究生招生计划动态调整探究——以成都理工大学为例[J].高教论坛，2022，（09）：101104.

[8]Francisco"Ruiz，Samira"El"Gibari，Jose"M.Cabello，Trinidad"Gomez，MRPWSCI：Multiple"Reference"Point"based"Weak"and"Strong"Composite"Indicators，Omega，2020，95（102060）：116.

[9]Francisco"Ruiz，Samira"El"Gibari，MRPPCI：A"Multiple"Reference"Point"Based"Partially"Compensatory"Composite"Indicator"for"Sustainability"Assessment.Sustainability，2021，13（1261）：119.