“整式的乘法”小试牛刀

一、选择题

1.下列选项中，从左到右的计算正确的是（ ）．

A. （2x）3=6x3 B. （ab）4=ab4

C.（2a5）2=4a25 D．（-m3）2=m6

2．若am=4，an=2，则a3m-3n的值为（ ）．

A．8 B．12 C．24 D．48

3．若（2x-4）0有意义，则x的取值范围是（ ）．

A．x≠0 B.x=2 C．x≠2 D.x=0

4．已知9x=m，277=n，则32x+3y等于（ ）．

A. 2m+3n B.mn C.m+n D.m2n3

5．已知a，b是常数，若化简（-2x+a） （x2+bx-3）的结果中不含x的二次项，则代数式-12a+24b-3的值为（ ）．

A．-3 B．2 C．3 D．4

二、填空题

6．计算：3x2y.（-2xy3）=______．

7．若单项式-6x2ym与1/3xn-1y3是同类项，则这两个单项式的积是_____．

8．若实数m，n满足2n-m+1=0，则4m÷16n=______．

9．若xx+1=1，则x的值为______．

10．已知（x-2） （x+m） =x2+3x-n，则m-n=______．

三、解答题

11．计算：

（1）-12024+（3-π）0-（-3）2；

（2）a·a3+（-2a2）3+a8÷a2.

12．已知2x-3y-2=0，求92÷（27y·3b3y）的值．

13.若a=255，b=344，c=533，试比较a，b，c的大小．

14．用“∪”和“∩”定义两种新运算：对于两个数a，b，规定a∪b=10a×10b，a∩b=10n÷10b.例如：3∪2=103×102=105，3∩2=103÷102=10.

（1）求211∪985的值；

（2）求2026∩2024的值：

（3）当x为何值时，x∪5的值与23∩17的值相等？

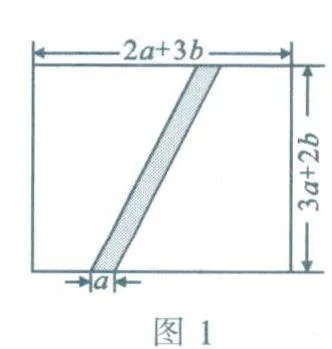
15．如图1，某小区有一块长为（2a+3b）m，宽为（3a+2b）m的长方形地块，物业公司计划先在该地块上修建一条平行四边形小路，然后将剩余部分进行绿化．已知小路的底边宽为am．

（1）用含a，b的式子表示绿化面积S．

（2）若a=2，b=4，求绿化的面积．

（参考答案在本期找）