“双碳”背景下城市轨道交通快慢车停站方案研究

摘 要：在“双碳”背景下，城市轨道交通将迎来绿色、低碳、高质量发展的重要机遇期。而随着客流在时空上分布的不均衡性越来越明显，站站停车的开行方案可能存在乘客出行时间长、企业运输能力浪费的问题。本文以快慢车运输组织模式为研究对象，考虑乘客出行成本，将快慢车的发车频率、快慢车的停站方案作为决策变量，综合考虑停车站数量、发车频率等约束条件，建立优化模型。以某条线验证模型的可行性，利用遗传算法求解最优停站方案，并得到优化效果。

关键词：双碳；客流；快慢车；停站方案；优化模型

中图分类号：U 29" " 文献标志码：A

随着城市轨道交通线网规模的不断扩张，其服务范围已经从市中心发展到郊区，为乘客带来了极大便利，同时，客流的时空分布不均衡性也越来越显著。城市轨道交通作为耗电量大、运行成本高的主要部门，充分利用线路条件，深度结合客流特征，合理分配运力资源，制定科学的列车停站方案，加快形成覆盖规划、设计、建造、运营、装备的城轨全生命周期，绿色低碳发展体系尤为必要，对城市轨道交通绿色发展具有重要的指导意义。

随着城市交通导致环境污染的情况加剧，越来越多的学者对城市交通的高碳排放问题进行研究。大力发展以轨道交通为主线的城市公共交通系统，国内外学者在低碳交通发展方面也已经取得了一定的学术成果。学者大多从客运组织、制动系统、供电系统等研究城市轨道交通的低碳发展。Aumnad Phdungsilp[1]主要研究城市交通，从公共交通入手研究低碳出行。刘浩博[2]从客运组织入手研究城市轨道交通碳排量。陈骞[3]从列车制动技术创新方面，研究城轨低碳发展战略。

1 问题描述

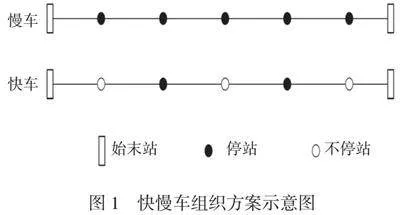
当客流分布不均衡时，可以采用快慢车的组织方案。如图1所示，快慢车方案一般情况开行两类列车，其中，慢车采用站站停车的方式，而快车可以在任意两站间直达，快车只需要停靠途中几个车站，这样缩短停站时间，从而缩短乘客的在车时间。乘客可以根据需要选择乘坐快车或慢车，既能满足乘客需要，又能提高运输效率。

因为快车并不是站站停车，缩短了某些车站的停站时间，所以逐步缩短与慢车的行车间隔，当快慢车的行车间隔接近最小行车间隔时，慢车需要在停车线上待避，快车越行慢车，从而快车在前，慢车在后，而后快慢车的行车间隔会逐渐变大。在城市轨道交通行车组织中，快慢车的运行速度接近，快车仅能通过节省部分车站的停站时间，并且慢车待避时会影响慢车的运行效率，因此本文只考虑同一方向上，快车越行一列慢车的简单越行情况，不考虑快车越行多列快车的复杂越行情况。

2 模型

2.1 基本假设

乘客均匀到达车站，并都能乘车，不存在滞留情况。

本文只考虑上行或者下行某个方向，另一个方向可以参照本方法重新计算。

本文只考虑高峰小时的停站方案，其他时间可以参照本方法重新计算。

慢车采用站站停车的方案，快车在某些车站停车，只考虑越行一次慢车。

快慢车的列车运行参数相同，包括各站停站时间、区间运行时分、定员等。

2.2 目标函数

城市轨道交通的服务对象是乘客，目标函数主要考虑乘客的利益，用乘客出行时间来表示乘客出行成本。当开行快慢车时，快车在某些车站不停站直接通过，此时有列车节省的停站时间，而在某些站快车不停站，会增加乘客的候车时间。如果乘客不能乘坐某种列车直达目的地，就会进行快慢车换乘，导致换乘时间增加。当快车越行慢车时，会增加越行时间，因此，乘客出行主要考虑列车节省的停站时间、乘客增加的候车时间、乘客增加的换乘时间和列车越行增加的时间。当乘客出行节省时间最大时，乘客出行成本最低，节省时间的计算过程如公式（1）所示。

maxT总=T1-T2-T3-T4 " " " " " " " " " " " " " " （1）

式中：T总为乘客出行节省的总时间，s；T1为列车节省的停站时间，s；T2为乘客增加的候车时间，s；T3为乘客增加的换乘时间，s；T4为由于列车越行增加的时间，s。

当考虑开行快慢车时，可以将每个OD客流的出行模式划分为4种情况。1）起点站和终点站都是快车站。2）起点站和终点站都是慢车站。3）起点站为慢车站、终点站为快车站。4）起点站为快车站、终点站为慢车站。

当起点和终点都是快车站时，乘客既可以乘坐快车，也可以乘坐慢车，不需要换乘。

当乘坐快车时涉及列车节省的停站时间、乘客增加的候车时间。其计算过程如公式（2）、公式（3）所示。

（2）

T21=Qij （tkh-th） " （3）

式中：T11 、T21分别为第一种情况时列车节省的停站时间、乘客增加的候车时间，s；Qij 为该小时从第i车站上车到第j车站下车的客流量；i，j，m 为车站索引，某条线路共N个车站，i，j，m∈{1，2...N} ；tm为m站列车停站时间（含启停附加时间），s；tkh为单个乘客快车的平均候车时间，s；th为站站停方案下单个乘客的平均候车时间，s。

当乘坐慢车时不涉及列车节省的停站时间，但是会有乘客增加的候车时间，计算过程如公式（4）所示。

T21=Qij （tmh-th）" " " " " " " " " " " " " " " " " （4）

式中：tmh为单个乘客慢车的平均候车时间，s。

当起点站和终点站都是慢车站时，乘客从起点到终点之间不经过或只经过一个快车站，乘客只能乘坐慢车直达终点。列车节省的停站时间、乘客增加的候车时间的计算过程如公式（5）、公式（6）所示。

T12 =0" " " " " " " " " " " " " " " "（5）

T22=Qij （tmh-th） （6）

式中：T12、T22分别为第二种情况时列车节省的停站时间、乘客增加的候车时间，s。

乘客从起点到终点之间经过两个及以上快车站，乘客在第一个快车站p换乘快车，再在最后一个快车站q换乘慢车，过程可用公式（7）、公式（8）表示。

（7）

T32=Qij（tmhk+tkhm） " " " " " " " " " " " " " " " （8）

式中：p，q为车站索引，某条线路共N个车站，p，q∈{1，2...N}；T32为第二种情况时乘客增加的换乘时间，s；tmhk为单个乘客慢车平均换乘快车的时间，s；tkhm为单个乘客快车平均换乘慢车的时间，s。

当起点站为慢车站，终点站为快车站时，乘客先乘坐慢车，到距离起点站最近的快车站p站换乘慢车。乘客先从i站乘坐慢车到p站，再从p站乘坐快车到j站。其过程可用公式（9）～公式（12）表示。

（9）

（10）

T23=Qij （tmh-th）" " " " " " " " " " " " " " " " "（11）

T33=Qij tmhk " " " " " " " " " " " " " " " " " （12）

式中：T13、T23、T33分别为第三种情况时列车节省的停站时间、乘客增加的候车时间、乘客增加的换乘时间，s。

当乘客先乘坐慢车到达快车站时，不涉及列车节省的停站时间，没有换乘，但是会有乘客增加的候车时间。

当起点站为快车站，终点站为慢车站时，P为距离起点站最近的慢车站。乘客先从i站乘坐快车到P站，再从P站乘坐慢车到j站。其过程可以用公式（13）～公式（16）表示。

（13）

（14）

T24=Qij （tkh-th） " " " " " " " " " " " " " " " " （15）

T34=Qij tkhm " " " " " " " " " " " nbsp; " " " " "（16）

式中：T14、T24、T34分别为第四种情况时列车节省的停站时间、乘客增加的候车时间、乘客增加的换乘时间，s。

综上4种情况，当起点和终点都是快车站时，涉及列车节省的停站时间、乘客增加的候车时间和越行时间；当起点和终点都是慢车站时，涉及乘客增加的候车时间和越行时间；当起点是快车站终点是慢车站，或者起点是慢车站终点是快车站时，涉及列车节省的停站时间、乘客增加的候车时间、乘客增加的换乘时间和越行时间。计算过程如公式（17）～公式（20）所示。

T1=xixjT11+（1-xi）（1-xj）T12+（1-xi）xjT13+xi（1-xj）T14

（17）

T2=xixjT21+（1-xi）（1-xj）T22+（1-xi）xjT23+xi（1-xj）T24

（18）

T3=（1-xi）（1-xj）T32+（1-xi）xjT33+xi（1-xj）T34" "（19）

T4=∑tyz " " " " " " " " " " " " " " " " " （20）

式中：tyz为单个列车越行慢车增加的时间，s。

2.3 约束条件

2.3.1 0-1约束

Xm、bm服从0-1约束，如公式（21）、公式（22）所示。

（21）

（22）

式中：bm为0，1变量，m站可以越行时为1，否则为0。

2.3.2 列车开行频率约束

系统设计远期最大能力应符合行车密度不小于30对/h[4]。如公式（23）所示。

F=F1+F2≤30 " " " " " " " " " " " " " " " " " "（23）

式中：F为快慢车的列车开行频率之和，列/h；F1、F2为快慢车的列车开行频率，列/h。

在营运时段，当列车正常运行时，最大运行间隔不应大于10 min。当列车行车间隔小于10 min时，可以用发车间隔的一半来表示整体客流的平均候车时间[5]，也就是乘客的候车时间不宜大于5min。则单个乘客的平均候车时间的计算过程如公式（24）所示。

（24）

单个乘客快车的平均候车时间及单个乘客慢车平均换乘快车时间的计算过程如公式（25）所示。

（25）

单个乘客慢车的平均候车时间及单个乘客快车平均换乘慢车时间的计算过程如公式（26）所示。

（26）

快慢车发车频率整数约束及快慢车发车频率成比例约束的计算过程如公式（27）所示。

（27）

2.3.3 停站约束

快车在两个端点站、换乘站必须停车，最多为站站停车，可以用公式（28）表示。

（28）

2.3.4 越行时间约束

当列车在快车站越行时，tyz取10s，否则取0。如公式（29）所示。

（29）

3 案例分析

3.1 基本参数

某地铁某线路自东向西共26个车站，线路如图2所示，由站线图可以看出，该线路未设置三线配线与四线配线的标准越行站，但在中间站中，第四、六、十三个车站的停车线设备可以满足慢车避让，快车越行慢车的条件。

列车在车站的停站时间主要分为开关门时间（取20s）和乘客的上下车时间（每位乘客0.6s）。需要综合考虑乘客上下车时间、开关门时间和启停附加时间，则各个车站tm的取值如下。tm={60，50，50，50，50，60，50，50，60，55，55，55，55，55，50，55，50，50，50，60，50，50，50，50，50，60}，部分区段客流分布图如图3所示。该地铁采用A型车6节编组，根据客流OD数据，计算得出F=8。

3.2 结果分析

将相关参数数据带入模型，利用遗传算法求解[6]。计算结果为：F1=2，F2=6。快车的停站车站为第{1，6，7，9，10，11，12，14，16，17，18，20，26}个车站。在此快慢车组合运行的方案下，平均每名乘坐城市轨道交通的乘客可以节省19.19s的出行时间。

4 结论

本文以最小化乘客出行时间为目标函数，以快慢车停车站数量、停站次数、上线列车总数等条件为约束，建立快慢车模式下的列车开行方案优化模型。将某地铁OD客流分布表及相关参数输入模型，得出最节省乘客出行时间的快慢车开行比例与快车停站方案，从而计算乘客出行时间节省，验证了模型的可行性与正确性，有利于促进城市轨道交通低碳发展。

参考文献

[1]AUMNAD PHDUNGSILP.Integrated energy and carbon modeling with a decision support system：Policy scenarios for low-carbon city development in Bangkok[J].Energy Policy，2010，2（38）：4808-4817.

[2]刘浩博.城市轨道交通对客运碳排放影响研究[D].大连：东北财经大学，2022.

[3]陈骞，张翔，薛江，等.电机械制动—“双碳”下的列车制动技术创新[J].现代城市轨道交通，2022（8）：93-97.

[4]北京市规划委员会.地铁设计规范：GB 50157-2013[S].北京：中国建筑工业出版社，2013.

[5]常秀娟，安飞，国冬梅，等.石家庄地铁1号线列车开行方案优化[J].交通节能与环保，2023，19（5）：270-274.

[6]张仲才.城轨列车车底运用优化研究[J].中国新技术新产品，2024（4）：111-113.

作者简介：杨素丽（1976-），女，河北石家庄人，就职于石家庄第五十三中学，中学一级教师，班主任。

高静（1986-），女，河北省秦皇岛人，就职于河北省秦皇岛市青龙满族自治县第二中学，中小学一级教师。

通信作者：常秀娟（1989—），女，河北保定人，硕士研究生，讲师，研究方向为交通运输工程。

电子邮箱：anf007@foxmail.com。

基金项目：河北轨道运输职业技术学院2024年度储备库课题“‘双碳’背景下城市轨道交通车底运用优化研究”（项目编号：GDKYZ2024105）。