烟囱定向爆破的动力学分析

摘 要：烟囱定向爆破对高大烟囱拆除具有重要意义。为了提升烟囱定性爆破过程的安全性，本文提出了一种动力学分析方法，由此构建了动力学分析过程和模型，模型中拉应力、压应力、剪切力、垂直支撑力等核心参数的计算，与烟囱倾倒过程中的倾角、中性轴后移角度建立了量化的关系。结果显示，倾角越大，烟囱倾倒的角加速度、角速度都越大。这种动力学方法给出了烟囱倾倒过程的量化分析结果，可以提升烟囱定向爆破的安全性。

关键词：皮带机械；皮带轮；旋压加工；锻压加工；有限元仿真

中图分类号： TU 746 文献标志码：A

在现代化城市中，因为生产需要和居民生活供暖需求等方面的原因，存在相当数量的高大烟囱。这些烟囱的绝对高度高，经过长期使用后就面临较大的安全隐患，必须予以妥善拆除[1]。高大烟囱的拆除一般有机械拆除法和人工拆除法。机械拆除法工作作业困难较大，人工拆除法则可能给操作人员带来较大的威胁和人身伤害[2]。因此，爆破法逐渐成为取代机械拆除法和人工拆除法的新方法。通过爆破完成高大烟囱的拆除任务，安全性、效率更高，并且成本低、性价比好。虽然爆破拆除具有许多优点，但也面临很大的安全隐患，这种压力主要来自烟囱周围环境的复杂性和爆破过程中的不确定性[3]。如果能有效地控制爆破过程，就能更全面地解决问题，包括爆破点位、爆破方向、爆破强度。为了能够按照预定的方向倾倒，就需要深入了解爆破过程的动力学特征，这也成为本文研究的切入点。

1 烟囱爆破中的失稳倾倒过程分析

在爆破拆除过程中，烟囱要从原有结构状态完成倒塌直到在水平地面平覆，才能完成整个爆破过程。炸药爆破导致部分结构断裂、断裂结构失去稳定性，再至逐步倾斜、倒塌和跌落。从技术的角度来看，这个称为烟囱的失稳倾倒，其整个过程一共包括4个环节：第一个环节，炸药爆炸在烟囱原有结构上形成爆破切口；第二个环节，中性轴形成并且位置逐渐向后移动；第三个环节，断裂的部分结构发生定轴旋转；第四个环节，断裂的部分结构塌落直至与地面接触并达成稳态。

从第一个环节来看，当爆破切口形成以后，烟囱对顶上部分的原有支撑结构大部分被破坏，只保留残余的支撑部分。这一部分的连接面积缩小，从而导致无法提供有效的支撑力，无法达成对顶上部分结构重力的平衡效果。从瞬时状态来看，爆破瞬间炸药的冲击力会使顶上部分有一个极为短暂的向上作用，但其后的时间内顶上部分的重力将全部集中作用在残余的支撑部分。这时进入第二个环节，烟囱原有的内部结构应力都需要重新调整，顶上部分在逐渐倾倒的过程中形成了中性轴，中性轴可以作为顶上部分倾倒的旋转轴，但这个中性轴的位置不是固定的，而是不断向后移动的。因此，第二个环节和第三个环节是不存在特别明显的界限的，中性轴在后移、顶上部分也在向下倾倒旋转。进入第四个环节后，残余的支撑部分进一步断裂，导致顶上部分从烟囱原有结构上彻底解体，并在重力的作用下开始跌落。

为了便于描述烟囱爆破过程中的失稳倾倒机理，给出说明，如图1所示。

图1为烟囱失稳倾倒的一个平面分析图，整个烟囱在爆破面上被划分为3个不同的区域，随着顶上部分不断倾倒，中性轴也不断向后移动。

爆破拆除预期效果的实现取决于爆破切口形成后，顶上部分的倾倒趋势所造成的应力是否会超出残余支撑部分的抵抗能力。因此，这里的应力分析是关键。残余支撑部分会同时受到拉应力和压应力的作用效果，如公式（1）、公式（2）所示。

（1）

式中：σF为烟囱顶上部分在倾倒过程中给残余支撑部分的拉应力；M为烟囱顶上部分在倾倒过程中所受到的倾覆力矩；m为烟囱顶上部分的质量；g为重力加速度；r为残余支撑部分的内部半径；A为残余支撑部分的横截面积；e为残余支撑部分的偏心距距离；I为残余支撑部分所受到的惯性矩。

（2）

式中：σD为烟囱顶上部分在倾倒过程中给残余支撑部分的压应力；M为烟囱顶上部分在倾倒过程中所受到的倾覆力矩；m为烟囱顶上部分的质量；g为重力加速度；β为残余支撑部分对应圆心角大小的一半；r为残余支撑部分的内部半径；A为残余支撑部分的横截面积；e为残余支撑部分的偏心距距离；I为残余支撑部分所受到的惯性矩。

2 烟囱爆破中的定向倾倒动力学分析

前面的工作分析了烟囱爆破过程中的失稳机理，并详细阐述了4个环节的状态。接下来，对烟囱爆破过程中的定向倾倒进行进一步的动力学分析。在整个烟囱的爆破过程中，爆破界面的顶上部分是否发生倾倒以及怎样倾倒是决定爆破成败的关键。在这一过程中，顶上部分还会伴随发生整体下坐、倾倒旋转过程中断裂、断裂后前冲或断裂后后坐等现象。

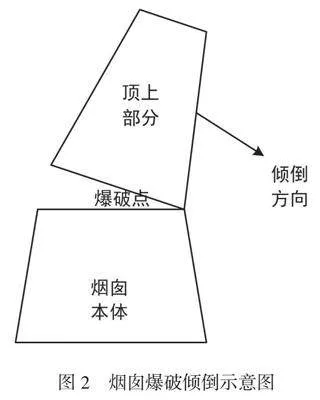
一旦顶上部分的倾倒趋势形成，那么必将以拉力、压力、剪切力等形式破坏顶上部分和烟囱本体的残余接触。残余接触部分一般会从外壁开始出现断裂，对由钢筋混凝土材料制成的烟囱来说，钢筋先会在顶上部分倾倒过程中被拔出拉脱，然后成型的混凝土被破坏。这一过程的示意图如图2所示。

在烟囱爆破倾倒过程中，顶上部分和烟囱本体的残余支撑所受到的剪切力如公式（3）所示。

（3）

式中：FQ为顶上部分和本体的残余支撑所受到的剪切力；θ为顶上部分脱离烟囱本体发生倾倒的旋转角度；θ0为顶上部分脱离烟囱本体即将发生倾倒的初始角度；m为烟囱顶上部分的质量；l为残余接触界面的中性轴到顶上部分中心的距离；ε为顶上部分脱离烟囱本体发生倾倒的加速度；H为脱离烟囱本体的顶上部分的高度；R为烟囱顶上部分的外径；K为烟囱顶上部分的外径的变化率；ω为顶上部分脱离烟囱本体发生倾倒的角速度；ω0为顶上部分脱离烟囱本体发生倾倒的初始角速度。

在烟囱爆破倾倒过程中，顶上部分和烟囱本体的残余支撑所受到的垂直支撑力如公式（4）所示。

FV=mg+[mlε+ω0H（2R-KH）][tanθcos（θ0+θ）-sin（θ0+θ）]-mlω2[tanθsin（θ0+θ）+cos（θ0+θ）] " " "（4）

式中：FV为顶上部分和烟囱本体的残余支撑所受到的垂直支撑力；θ为顶上部分脱离烟囱本体发生倾倒的旋转角度；θ0为顶上部分脱离烟囱本体即将发生倾倒的初始角度；m为烟囱顶上部分的质量；l为残余接触界面的中性轴到顶上部分中心的距离；ε为顶上部分脱离烟囱本体发生倾倒的的加速度；H为脱离烟囱本体的顶上部分的高度；R为烟囱顶上部分的外径；K为烟囱顶上部分的外径的变化率；ω为顶上部分脱离烟囱本体发生倾倒的角速度；ω0为顶上部分脱离烟囱本体发生倾倒的初始角速度。

3 烟囱定向爆破动力学试验分析结果

在前面的工作中，对烟囱定向爆破过程中失稳倾倒的4个环节进行了阐述并分析了其动力学机理。为了提升烟囱定性爆破过程的安全性，本文提出了一种动力学分析方法。在这一方法中，烟囱定向爆破的失稳过程被划分为4个环节，进而对烟囱倾倒过程中的拉应力、压应力、剪切力、垂直支撑力进行力学建模。在接下来的工作中，将通过试验对烟囱定向爆破过程中的动力学特性进行验证。

在试验过程中，选取了2个实际的爆破案例，第一个案例中的烟囱高度为180m，第二个案例中的烟囱高度为210m。2个案例中的烟囱均为钢筋混凝土结构，混凝土材料的密度为3000kg/m3。试验环境中取自然风速，风速大小为2.0m/s。第一组试验先考察烟囱定向爆破倾倒的角度和中性轴后移过程中的角度变化关系，结果如图3所示。按照公式（3）和公式（4）计算倾角，而公式（3）和公式（4）的部分参数计算需要使用公式（1）和公式（2）。为了便于说明数据产生的过程，以烟囱倾角为θ=0.48°为输入，计算中性轴后移角度。

此时，各参数的值如下：烟囱倾角θ为0.48°，即将发生倾倒的初始角度θ0=44.52°，烟囱脱离本体的高度H=80m，烟囱顶上部分的外径R=2m，顶上部分脱离烟囱本体发生倾倒的加速度ε=0.03m/s2，重力加速度g=9.8m/s2，烟囱顶上部分的外径的变化率K=0.03，顶上部分脱离烟囱本体发生倾倒的初始角速度ω0=0.05rad/s，顶上部分脱离烟囱本体发生倾倒的角速度ω=0.11rad/s，表示顶上部分和烟囱本体的残余支撑所受到的垂直支撑力FV=6012N，根据公式（1）和公式（2）得到，烟囱顶上部分的质量m=40000kg，将上述数据代入公式（4），可以计算出中性轴到顶上部分中心的距离l=90m，又因为烟囱高度为180m，所以可以计算中性轴后移角度为60°。

由此可知，当横坐标烟囱倾角θ为0.48°时，纵坐标中性轴后移角度为60°。

按照同样的方法可以得到图中曲线上各组对应数据，从而绘制出曲线结果，如图3所示。

在烟囱定向爆破的过程中，烟囱顶上部分的倾斜角度越大，中性轴后移的角度变化越小。2个高度的烟囱都表现出了这个共同的特征。但相对来说，烟囱高度越高，这种方向的关系越剧烈；烟囱高度越低，这种方向的关系越舒缓。

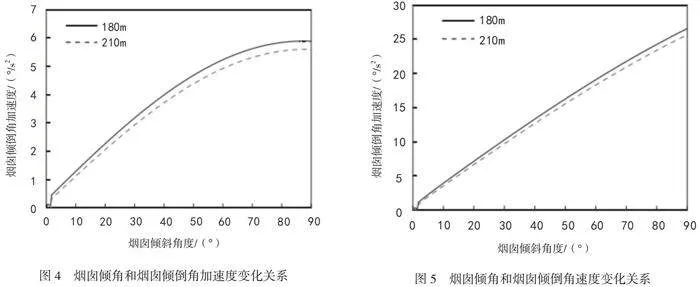
第二组试验考察烟囱定向爆破倾倒的角度和烟囱倾倒的角加速度变化关系，结果如图4所示。

由图4可知，在烟囱倾倒过程中，倾角越大，烟囱倾倒的角加速度越快。在起初阶段，烟囱倾角和烟囱倾倒角加速度变化关系接近线性变化。其后，二者的关系接近水平直线。这一组试验结果也表明，烟囱高度的差异对二者关系变化曲线影响不大，只有幅度上的微小减弱。

第三组试验考察烟囱定向爆破倾倒的角度和烟囱倾倒的角速度变化关系，结果如图5所示。

由图5可知，在烟囱倾倒过程中，烟囱倾角和烟囱倾倒角速度变化关系始终接近于线性变化。烟囱倾角越大，烟囱倾倒角速度越快，并且这种关系不受烟囱高度差异的太大影响。

综上所述，在试验过程中，选取180m和210m的2个烟囱爆破案例作为试验对象，对烟囱倾角-中性轴后移角度、烟囱倾角-烟囱倾倒角加速度、烟囱倾角-烟囱倾倒角速度3组曲线进行试验验证和试验过程分析。综合3组试验的分析可以看出，烟囱倾角越大，中性轴后移的角度会越小，而烟囱倾倒角速度和角加速度会越来越快。可见，运用动力学的分析方法可以得到几个关键参数的量化分析结果，可以对烟囱爆破过程的安全性进行预判。

4 结语

从4个环节对烟囱定向爆破过程中的失稳倾倒进行分析：第一个环节，炸药爆炸在烟囱原有结构上形成爆破切口；第二个环节，中性轴形成并且位置逐渐向后移动；第三个环节，断裂的部分结构发生定轴旋转；第四个环节，断裂的部分结构塌落直至与地面接触并达成稳态。基于此，构建了烟囱定向爆破的多参数动力学分析模型，从而对2个实际的定向爆破案例进行动力学分析。试验结果得到的3组曲线变化证实了可以通过动力学分析有效地控制烟囱定向爆破过程，从而提升爆破过程的安全性。

参考文献

[1]费鸿禄，段宝福.风载对筒形高耸建筑物定向爆破倾倒过程影响的研究[J].爆炸与冲击，2023，20（1）：92-96.

[2]郑炳旭，魏晓林，陈庆寿.钢筋混凝土高烟囱爆破切口支撑部破坏观测研究[J].岩石力学与工程学报，2021，25（2）：3513-3517.

[3]褚怀保，徐鹏飞，叶红宇，等.钢筋混凝土烟囱爆破拆除倒塌与受力过程研究[J].振动与冲击，2022，34（22）：183-186.