基于预测案例的马尔科夫链教学方法研究

摘 要：马尔科夫链由于其对过去、现在、未来状态关系的物理内涵，是实际工程经常运用的数学概念，多用于对未来状态的预测，广泛应用于态势估计、模型构建、趋势预测等方面中。在高校随机过程课程安排中，针对马尔科夫链的教学内容公式化，学生理解较浅，不利于工程实践能力培养。该文重点采用案例教学法，以飞机目标跟踪预测实际工程案例为主线，马尔科夫链物理内涵实现的课程内容为辅线，结合生活中诸多案例讲授本节课程的教学重点及其应用，激发学生对随机过程课程的探索兴趣，锻炼学生自主思考能力。课程强调理论与实践相结合体系，提升学生运用课程内容解决实际问题的能力，并根据马尔科夫链的物理内涵，启发学生保持对未来积极向上、努力拼搏的精神。

关键词：马尔科夫链；随机过程；案例教学法；目标跟踪预测案例；课程思政

中图分类号：G642 文献标志码：A 文章编号：2096-000X（2024）35-0023-06

Abstract： Markov chains， due to their physical implications regarding the relationships between past， present， and future states， are concepts frequently applied in practical engineering， primarily for future predition. They are widely used in situation estimation， model construction， trend forecasting， and other areas. In the course design for stochastic processes at universities， the teaching content on Markov chains is too formulaic for students to develop a deep understanding and hindering the cultivation of engineering practice skills. This paper focuses on the case-based teaching method， using an engineering example of aircraft target tracking and prediction as the main thread， supplemented by cases from daily life， to explain the concept and physical significance of Markov chains. This approach emphasizes the mathematical content and their applications， encouraging students to think and explore engineering problems independently. The course integrates theory with practice to enhance students' ability to solve real-world problems using theoretical content. Additionally， based on the physical implications of Markov chains， students are guided to maintain a positive and proactive outlook on life， striving for success in the future.

Keywords： Markov chain; stochastic process; case-based teaching method; target tracking prediction case; course moral education

随机过程理论作为一门应用数学学科，由于在工程实践中广泛应用，是当前高校必选专业课程之一，具有专业性强、内容抽象深奥、概念知识繁多等特点[1]，在传统“灌输式”教学方式中，教师授课“重讲，轻应用”，导致学生缺失理论与实际应用相联系能力，众多学生反映这门课程教学体验单一、内容深奥难懂等问题[2]，难以实现提升学生数学理论实际应用、概念公理深层次理解的课程教学目标[3]。

马尔科夫链是随机过程理论课程中马尔科夫过程这一章节的基石，既具备马尔科夫过程的物理特性与内涵，形式上相对简单，在课程内容体系架构上，又是马尔科夫过程的基石，学生的有效理解有利于课程循序渐进、由浅入深[4]。同时，马尔科夫过程，包括马尔科夫链，具有基于过去状态对未来状态判定的物理含义[4]，在实际生活、科研工程中对未来状态的预测有着广泛的应用与影响[5-7]，是本门课程理论应用于实际一重大实现，在当前科研环境中依旧基于马尔科夫理论进行相关研究，因此马尔科夫链的学习是学生体会数学知识在生活、工程问题中灵活应用的关键节点，引导学生理解领悟马尔科夫链内容内涵具有较高的教学价值。

在实际教学过程中，课程本身具有强烈的数学色彩，使得普遍教学方法倾向于围绕数学推导进行严谨分析。数学分析环节必不可少，但过于依仗数学分析的传统教学方式下，学生容易对课程内容产生抵触心理，而且不利于锻炼学生自发思考、实际应用的能力，导致教学成效甚微。近年来，为激发学生学习积极性，许多教师将新式教学方法引入课堂，如比照推演法[8-10]、案例法[2-3，10]、思政法[2，10]等，在课程讲授过程中穿插使用，提升了学生对课程的接受程度。针对随机过程数学严谨性与应用性较强的课程，不能降低对数学逻辑推导的比重，同时应该灵活运用多种教学方式，通过让学生从实际工程中发现问题，利用理论知识进行分析，最终回到现实中寻找解决方案。

本文以马尔科夫链课程的教学为研究对象，采用进一步演化的案例教学法，将飞机目标跟踪预测这一复杂工程案例[5-7]贯穿课程主线，结合比照推演和思想政治引导等教学手段，力求在理论与实践结合的基础上深化教学效果。通过穿插比赛、天气等具有实际参照意义的小案例辅助讲解，逐步引导学生在动态思考中深入理解马尔科夫链的核心概念和基础理论，提高其分析和解决现实问题的能力。在教学设计上，教学方式强调从实际问题出发，通过理论框架的逐步渗透，学生不仅能掌握马尔科夫链的数学基础与推演方法，还能应用这些理论工具于复杂的工程场景中进行预测与优化。与此同时，教学过程中融入思政教育，利于帮助学生形成科学的世界观、人生观和价值观，引导他们在知识学习和应用过程中树立积极的社会责任感和职业操守。此种教学模式为高校教师提供了具有创新性和实践性的教学参考，对于提高学生的理论素养和实践能力，具有广泛的借鉴意义。

一 教学内容

（一） 目标跟踪预测案例与马尔科夫链的联系

目标跟踪预测是实际应用马尔科夫链的工程任务之一，是我国维护国家安全、领土完整的重要手段。以飞机目标为例，为及时阻止可疑目标进入我国领空，需要在侦查捕获该目标位置、速度等状态信息时，预测其未来状态，从而进行拦截[9]。这一目标跟踪预测任务就包含三类信息，以目标捕获的时刻为当前时刻，捕获前为过去状态信息，需要预测的是未来状态信息[7]。为保证预测结果尽量准确，一般采用通过提取较多过去状态信息进行趋势、规律分析，提高预测准确率；而实际上由于目标可能存在来源不明的情况，过去状态信息不足，可以通过马尔科夫链这一数学概念，明确“目标未来时刻位置只与当前时刻位置有关，而与过去时刻状态无关”的物理内涵从而解决位置预测的问题。

在本节课程内容全部讲授完毕时，重新回顾目标跟踪预测案例，将马尔科夫链应用到目标运动状态预测中，对未来某时刻目标位置预测关联简化到只与最近一次跟踪所得目标信息有关，降低模型复杂度，构建目标状态模型。最终对比实际轨迹与预测轨迹结果，差异较小，以实际案例阐述了马尔科夫链在预测问题上的应用，类推其他工程应用实际预测问题。

（二） 重难点分析

1 重点内容

1）转移概率的概念：围绕由当前状态去预测未来状态的核心问题，在引入马尔科夫链之后，理解未来状态的预测可以通过马尔科夫链降维，具体是如何进行预测的呢？基于足球比赛结果预测、天气预测案例，理解基本（一步）转移概率，到k步转移概率，k步转移矩阵的概念；明确条件概率在转移概率中应用的内涵，明晰步数与状态对应关系。基本转移概率即为已知最近一次的状态，预测下一次的状态；类推到k步转移概率，即为已知最近一次的状态，预测k次后的状态。这里的“次”就是步数，通常指均匀采样的时刻；状态是随机序列状态空间中的一种可能。而将k步转移概率以状态空间到状态空间的形式排列，即形成高维的k步转移矩阵。

2）切普曼-柯尔莫戈罗夫方程及其推导过程：基于转移概率的概念，基本转移概率与k步转移概率存在步数上的差异。基本转移概率只有一步，忽略步数与条件概率的表达方式相同，获取统计结论较为容易；而需要转移k步时，迭代次数增多，难以获取准确的统计结果。引导学生思考如何获取k步转移概率，增加中间过渡态，推导得出k步转移概率可以将步数分为两组乘积求和的形式，从而得到切普曼-柯尔莫戈罗夫方程。

3）齐次马尔科夫链的概念：在熟悉了马尔科夫链、转移概率、切普曼-柯尔莫戈罗夫方程的数学公式后，引入齐次性的概念，一般情况下转移概率是与当前时刻、状态相关的条件概率，齐次性的加持使之简化为与当前时刻无关的条件概率，具有平稳转移概率的特性。由于转移概率不受初始时刻约束，齐次k步转移概率与齐次k步转移矩阵均可应用切普曼-柯尔莫戈罗夫方程简化为基本转移概率与基本转移矩阵的幂函数形式，指数为步数k。结合天气预测案例，齐次性可以大大简化问题难度，将k步预测降维为一步预测。虽然齐次马尔科夫链具有预测问题简化的能力，但要注意这里的齐次性，即转移概率与时刻无关的前提条件。

2 难点内容

马尔科夫链的概念是由目标跟踪预测工程实例引出的，对于不熟悉马尔科夫性的学生来说，是全新的数学概念，通过目标跟踪预测案例思考如何用目标当前状态科学合理预测目标未来状态的问题，引入概念，明确马尔科夫性是只考虑最近一次结果预测未来结果的特性，并非纯粹无记忆性，也具有无后效性的特征。用数学方式表示过去、现在与未来的对应时刻与状态后，结合条件概率的定义，得出马尔科夫链的数学公式，其物理内涵是在离散的时间序列中，定义离散的状态，未来状态只与现在时刻状态有关，与过去状态无关。

马尔科夫链的数学公式中等式两侧均为转移概率，过去、现在、未来对应到时刻，状态为状态空间中的一项，转移概率是一个时刻到未来一个时刻状态转移的条件概率。为计算时刻相差多个采样数后转移概率，即k步转移概率，分为两次进行转移，推导出切普曼-柯尔莫戈罗夫方程，将k步转移概率分解为两次较低维度转移。引入齐次性后，就可以降为基本转移概率的幂。从数学计算角度说明了对未来状态预测所需的当前状态参量，以及所需的计算方法，作为完整的马尔科夫链课程内容讲述，以问题引入由果溯因，回答如何预测未来状态的问题。

二 关键教学环节设计

（一） 目标跟踪预测案例主线设计

将目标跟踪预测案例作为课程主线，从解决工程问题的角度引入核心课程内容，引导学生思考，激发学生学习兴趣，提升学生工程应用能力，促使学生自发思考探索，达成课程学习最终目标。

主线设计主要体现在两方面：首先由目标跟踪预测案例引入，抛出未来状态预测的解决方法，进入课程教学内容；在课程内容的重难点随着问题逐步解决渐渐明确叙述后，重新审视目标跟踪预测问题，运用课程内容，直接给出解决方案，说明其可行性。这样是以先倒序阐述，后正序说明的方式，梳理目标跟踪预测案例解决思路，便于学生理解。

1 预测案例引入

在课程的开始，引入预测类问题，如未来的天气、股价，自动驾驶中的行为预测、输入法推测接续的词语等等[8]。在诸多的预测应用实例中，选择科工关键的目标跟踪预测案例进行具体介绍，以飞行目标为例，需要关注三个层面的问题：①目标从何处来？在目标被探测之前，这些信息是未知的。②目标的当前状态怎样？目标被探测到之后，可以获取位置、速度等信息。③目标下步去哪？也就是最重要的预测类问题，即雷达能否用当前状态的有限信息，求解目标跟踪预测的问题。

通过具体案例的分析引发学生对未来状态预测问题的思考，怎样才能由目标当前状态预测目标未来状态呢？从而引入马尔科夫链这一解决途径，进入课程内容叙述。

2 预测案例应用

在对以上教学重点与难点内容完成讲授后，未来状态预测问题由马尔科夫链降维到计算参数量较低的转移概率，证明切普曼-柯尔莫戈罗夫方程得出多步转移概率计算方式，引入齐次性降低计算难度，到此未来状态问题从马尔科夫链的方向得到完全的解决方案。重新思考课程开始的目标跟踪预测案例，明确马尔科夫链在目标跟踪状态建模的作用，实现理论基础在实际工程中的应用。

假设目标做一维匀速直线运动，目标初始位置为x0，目标速度为？淄，根据牛顿运动方程，目标的位置处于x=x0+？淄·t。假设对目标运动情况进行离散采样（时间间隔为T），则目标在不同时刻的位置可由下式迭代计算得到[8]

式中位置x的下标为时刻。在当前案例中，可以认为每次采样目标运动状态相互独立，且第k+1时刻目标的位置xk+1可仅有由k时刻目标位置xk、速度？淄以及采样间隔T决定，故此过程可以看作是马尔科夫链，可只考虑最近一次采样目标状态对未来状态预测的影响。由此，通过牛顿运动方程x=x0+？淄·t建立目标离散状态模型xk+1=xk+？淄·T。

将目标运动状态以Xk=[xk，？淄k]T表示，也就是系统状态；离散状态模型可建模为Xk+1=F·Ｘk，实际中考虑运动过程噪声可建立运动目标模型为Xk+1=F·Ｘk+Wk，其中F=1 T0 1为状态参数矩阵，Wk=Wk ，xWk ，？淄为服从高斯分布的过程噪声。在实际应用中目标状态通常延伸到三维空间，此时目标运动状态可构建为Xk=xk，？淄x，yk，？淄y，zk，？淄zT，F，Wk维度相应上升。估计F，Wk即可预测得到Xk+1未来状态。

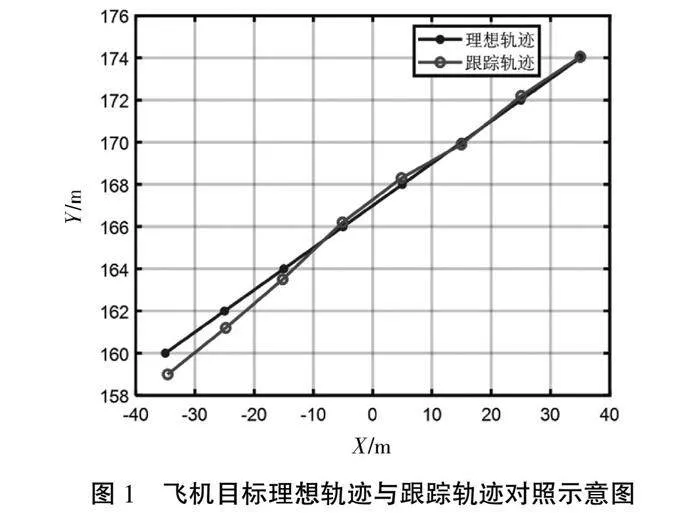
实际上由于估计总会出现误差，工程中常常使用卡尔曼滤波进行状态与误差的反馈迭代与更新，使预测结果更为准确。图1是依据马尔科夫链构建的目标运动状态模型经过卡尔曼滤波后得到的理想轨迹，以及实测飞机目标跟踪轨迹的示意图，可以发现轨迹预测准确度较高。随着转移步数的增多，误差也有所增大，因此根据当前状态可较准确预测到的未来状态也是有限的，鼓励同学们自发探索如何进一步提高模型构建可预测能力。

图1 飞机目标理想轨迹与跟踪轨迹对照示意图

总体来说，目标下一时刻的位置和状态只与当前时刻的位置和状态有关，受过去时刻状态影响较小，体现了马尔科夫链无后效性的特征。

（二） 马尔科夫链教学内容辅线设计

通过主线目标跟踪预测案例提出的问题，一层一层抽丝剥茧，分析已知量与未知量，逐步将复杂问题简单化。以提出问题，分析问题，解决问题，再提出新的问题的方式，站在学生的思考逻辑中进行教学讲授。根据本课的教学重点与难点，通过下述问题引入课程关键内容：

①如何根据目标当前状态预测目标未来状态？引入马尔科夫链，分析马尔科夫特性，给出马尔科夫链数学定义，降低未来状态预测维度。②根据马尔科夫链数学公式，引入转移概率。转移概率是如何定义的？与哪些参数有关？转移概率是特殊的条件概率，与已知状态的时刻、未知状态时刻和状态空间的项有关。③k步转移概率如何获取？引入状态转移过渡时刻，将k步分为两次转移实现，即可将k步转移概率降维到步数更少的转移概率计算中，得到数学公式复杂的切普曼-柯尔莫戈罗夫方程。④若假设同一采样率下随机过程的转移概率不受时刻影响，即齐次性条件下，k步转移概率如何获取？引入齐次性，更新切普曼-柯尔莫戈罗夫方程，得到齐次性马尔科夫链定义，由k步降维为一步的幂函数。

通过环环相扣的问题引导，教学思路利于学生理解并接受逻辑性、数学性较强的课程内容，形成思路闭环，明确课程内容框架。

1 马尔科夫链

由目标跟踪预测案例引入，预先告知学生马尔科夫链是该预测问题的解决方案。在讲述具体数学公式前，先让学生理解什么是马尔科夫，以两支队伍足球比赛结果预测为例，随机过程根据记忆特性可以分为三类：①纯粹随机过程：不考虑两支球队的过去表现进行预测。②马尔科夫过程：只考虑两支球队最近一次比赛的成绩进行预测。③非马氏过程：考虑两支球队过去的诸多成绩，或者全部成绩，进行预测。

为准确描述马尔科夫过程在过去、现在、未来状态关系，具体说明马尔科夫链的定义：马尔科夫链是状态和时间均为离散值的马尔科夫过程[2]。设存在随机序列{Xn，n∈N+}，其状态空间S={a1，a2，…，an}，对所有的n∈N+，有：

其定义的主要两个部分为状态a■和时间n，描述了状态随时间变化的规律。可以看出，若将时间n-1设为现在，n设为未来，n-2，n-3，…，1设为过去，则上式描述的含义为：系统的现在状态已知，那么系统未来的状态与过去的状态无关，只与现在状态有关。这就是马尔科夫链的特性——无后效性。

由定义即可看出马尔科夫链的特性，然而对于初次接触马尔科夫过程的学生来说，理解只局限于其数学公式。观察马尔科夫链表达式，为进行未来状态的预测，对条件概率降维简化，得到的条件概率叫作转移概率，为明晰转移概率的物理概念，进入下一步的课程学习。

2 转移概率

将转移概率的定义具体分析为下式

式中：i，j∈S，表示系统从m时刻到n时刻，共经过n-m的时间后，状态由i转换成j的概率。S为状态空间，X为序列，a为对应的状态。m时刻的状态i可以理解为当前状态是已知条件，因此转移概率的本质为条件概率，具有如下的性质：

pij（m，n）≥0

从m时刻开始，若只转移一步，状态由i转换成j，即基本（一步）转移概率定义如下：

从m时刻开始，若转移k步，状态由i转换成j，即k步转移概率定义如下：

考虑到整个状态空间的转移概率，即可得到k步转移矩阵定义如下：

转移概率可用来描述马尔科夫链不同时刻不同状态之间的转移特性，为辅助学生理解，以天气预测案例为例进行补充说明。

在这个例子中，我们将天气可能性，即状态空间中的项限制为3种，雨天、雪天、晴天；我们研究的对象是在一段时间内每一天的天气，因此这段时间内的天气就形成了随机序列，以1天为采样间隔。假设明天的天气只和今天的天气有关，和昨天及昨天之前都无关，天气状态序列就形成了一个马尔科夫链，体现了“化繁为简”的降维思想，将n个时刻的n维问题变成2个时刻的2维问题。定义雨天、雪天、晴天之间的转移概率，从而形成一步转移概率矩阵：

定义矩阵的行表示当前状态，列表示未来状态，从上到下、从左至右分别为雨天、雪天、晴天状态。

若已知今天下雪的概率为0.3，那么明天晴天的概率即可通过0.3×0.1=0.03获得。通过天气预测案例，加深学生对转移概率的理解。

3 切普曼-柯尔莫戈罗夫方程

从统计学角度来说，基本转移概率已知，获取较容易，但k步转移概率由于复杂度较高，应如何求解呢？以天气预测为例，如果想知道后天、大后天、未来一周的可能天气概率，又该如何计算呢？

由上述推导可得出切普曼-柯尔莫戈罗夫方程：

该方程针对马尔科夫链，给出其k步转移概率计算方式，即用两部分转移概率的乘积求和计算k步转移概率，可逐步分解到一步转移概率进行计算。

4 齐次马尔科夫链

学习了切普曼-柯尔莫戈罗夫方程后，虽然可以计算k步转移概率，但是在k比较大的情况下，即使使用二分法也要乘积求和多次，计算起来较困难。故引入齐次的概念，简化计算。

“齐次”的含义是系统的转移概率与时间无关，即具有平稳转移概率。与时间无关，则齐次马尔科夫链的定义简化如下：

在此基础上，可以根据其一步转移概率写出转移概率矩阵：

同样地，在齐次前提下，转移概率矩阵也与时刻无关。

在此基础上引入齐次马尔可夫链满足的切普曼-柯尔莫戈罗夫方程：

上式表示齐次马尔科夫链可由一步转移概率确定k步转移概率，即可知齐次马尔科夫链的初始分布和转移概率即可确定其有限维分布。

再次回顾天气预测案例。已知雨天、雪天、晴天之间的转移概率，第一天下雪，则第五天是晴天的概率是多少？根据齐次马尔科夫链和一步转移概率定义，求解未来任意一天的气象状态可以由迭代运算分步实现，已知一步转移概率可完全确定k步转移概率，即引出切普曼-柯尔莫戈罗夫方程：

由上式可求得气象预测问题的五步转移概率：

。

即可知第一天下雪概率0.3，则今天下雪，第五天是晴天的概率为0.294 5，则第五天为晴天的概率是0.3×0.294 5=0.088 35。天气预测案例生动形象地加深了学生对新概念和定理的理解，并通过利用新概念解决问题，形成“学以致用”的良性循环，进一步梳理巩固马尔科夫链的教学逻辑链。

（三） 马尔科夫链反映出的课程思政

马尔科夫链的本质是未来状态仅由当前状态决定，不受过去状态影响，是一种有限记忆性，无后效性。工程上经常应用马尔科夫链进行降维操作，简化或者说弱化过去状态对未来状态的影响，利用有限的信息进行预测。马尔科夫链的物理内涵正如陶渊明所作《归去来兮辞》中的一句话，“悟已往之不谏，知来者之可追”，过去的错误已经不可挽回，但未来的事还值得去追寻。过去的状态已经发生了，但马尔科夫链告诉我们，把握当下的状态，才是对未来状态的最好影响，不要拘泥于遥远过去，请放眼充满可能性的未来。

三 结束语

为培养学生应用课程理论知识解决工程实际问题的能力，加深学生对课程知识的理解，本文介绍了以预测类案例为引导的马尔科夫链教学方案，课程教学以目标跟踪预测问题为主线，结合球赛预测、天气预测等小案例，将马尔科夫链教学重点与难点按照倒序的方式，以学生思考问题的思路逐步剖析并阐述概念与内涵，巧妙地将数学公式与推导和预测案例融合在一起，加深学生对理论知识的思考，培养学生善于分析问题、解决问题的理论应用能力。在此基础上，针对目标跟踪预测案例，讨论目标跟踪建模中的马尔科夫特性，明确马尔科夫链在此类预测案例中的应用方法，引导学生对马尔科夫特性的深层次思考，培养健康向上、积极进取的拼搏观、价值观。

本文设计的教学方案在帮助学生熟练掌握马尔科夫特性的同时，也是一种教学方案的革新，提升工程案例在课程讲解中的比重，将课程内容与案例有效结合，有利于提升学生对课堂内容的掌握程度，提高学生研习的积极性与主动性，锻炼学生思维，有效实现学生能力培养。

参考文献：

[1] 杨炼.高校数学类课程案例式实验教学方法研究[J].教育进展，2023（5）：2468-2473.

[2] 杨威，曾虹程，门志荣，等.各态历经性的案例教学法研究[J].高教学刊，2024（22）：7-11，15.

[3] 江滢.从“案例举例”到案例教学——案例教学法在我国法学实践教学中的应用与完善[J].科教文汇，2024（15）：101-104.

[4] 周荫清.随机过程理论[M].北京：电子工业出版社，2006.

[5] 郭军，朱凡，刘远飞.基于马尔科夫链预测的多无人机协同搜索控制[J].弹箭与制导学报，２００７（５）：３１５-318.

[6] 王泽天，高岭，高全力.基于改进马尔科夫链的移动轨迹预测方法[J].西安工程大学学报，２０２０，３４（２）：９７-102

[7] 白晓兰，张振朋，周文全，等．基于采样隐马尔可夫模型的移动机器人路径规划[J].组合机床与自动化加工技术，２０２３（７）：５０－５６．

[8] 陈建华，李海燕，张榆锋，等.《随机过程》精品课程建设与教学改革探索[J].中国科技信息，２０１０（１８）：２８３－284.

[9] 熊丹，吴传菊.工科研究生随机过程课程教学改革研究[J].高师理科学刊，２０１５，３５（１）：６７－70.

[10] 徐华平.比照推演式教学方法在工科“随机过程理论”课的应用[J].高教论坛，２０１１（１１）：４１－４３.