基于t-SNE 特征降维和K 近邻的分类算法

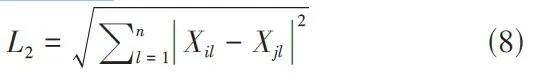
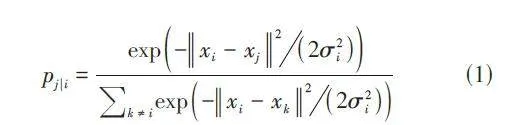
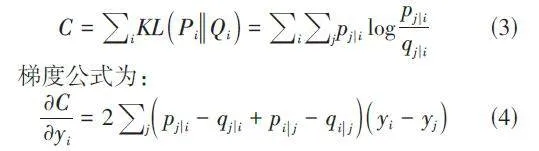
摘要：针对使用机器学习和深度学习算法进行分类、识别任务时容易出现维度灾难的问题，本文提出了一种基于t-SNE特征降维与K近邻的分类算法。首先，分别使用主成分分析法（PCA）和t-SNE算法对特征数据进行降维，然后利用K近邻算法进行分类预测。在手写数字数据集和鸢尾花数据集上进行了实验。实验结果表明，本文提出的基于t-SNE特征降维与K近邻的分类算法在手写数字数据集上的准确率达到98%，比PCA算法高出约20%；在鸢尾花数据集上的准确率为97%。此外，该算法即使在维度降低幅度较大的情况下，仍能保持较高的分类准确率，同时维度降得越低，算法所需时间越少，且对不同数据集展现出较强的适应性。

关键词：数据降维；分类算法；K近邻；聚类算法

中图分类号：TP391文献标识码：A

文章编号：1009-3044（2024）34-0011-03开放科学（资源服务）标识码（OSID）：

0引言

随着数据时代的到来，数据量不断增长，数据的维度也越来越高。数据维度增加意味着信息量更大，为决策提供了更多依据。然而，高维数据的处理需要消耗大量计算资源，计算时间显著增加，同时冗余数据和噪声信息可能影响实验结果，导致准确率降低和可用性较差的情况，甚至引发“维度灾难”[1]。对此，采用降维算法获取数据的本质特征，可以缩短计算时间并提高后续算法的准确率。

数据降维的核心在于提取数据内在的本质特征，从而减少冗余信息和噪声对结果的负面影响，提高算法的准确性和效率。常见的降维算法包括低方差滤波[2]、高相关滤波[3]、主成分分析（PCA）[4-9]、线性判别分析（LDA）[10-14]等。

其中，主成分分析（PCA）是一种应用广泛的降维方法，在医学、航空、光谱等领域均有重要应用。例如，谢凡等人[4]利用主成分分析、聚类方法以及BP神经网络对湍流MILD燃烧初始着火过程进行了研究；杨文锋等人[5]基于PCA和SVM研究了飞机蒙皮激光分层除漆过程中的LIBS在线监测问题；王磊等人[6]通过PCA实现DME信号的特征增强，并结合卷积神经网络有效检测DME信号；张楠等人[7]采用PCA-BP模型准确预测了脑卒中患者行走时髋、膝、踝关节的力矩。

此外，LDA降维技术应用也十分广泛。例如，刘佳悦等人[10]利用LDA降维和BP神经网络对手写数字进行识别；荀鹏等人[11]采用LDA-KNN分类模型实现了岩体的非线性分级预测；靳文哲等人[12]改进了LDA算法以提升织物图像的分类准确率；彭灿华等人[13]将LDA主题模型与曲波阈值和ICEEMDAN方法结合，对数据库中的数据进行降噪处理以提高挖掘效率。

上述研究大多是针对某一特定数据集设计的分类方法，在不同类型的数据集上不一定具有良好的适用性。因此，本文提出了一种通用的分类算法。算法首先使用t-SNE算法进行特征降维，然后结合K近邻（KNN）算法完成分类任务。本文采用手写数字数据集和鸢尾花数据集进行实验，通过对比多组PCA降维算法实验结果，验证该通用分类算法的效果和适用性。

1基本原理

1.1t-SNE算法

t-SNE（t-distributedstochasticneighborembed⁃ding）降维算法是一种非线性降维的机器学习算法，能够在降低向量维度的同时很好地捕捉原始数据的复杂流形结构[15]。其主要思想是将高维空间中的数据点通过概率分布反映点与点之间的相似度，并通过优化低维数据分布的方式来尽量保持高维空间中数据的邻域结构。

具体来说，t-SNE首先将高维欧几里得距离转换为条件概率，用来表达两点之间的相似度。给定高维空间中的数据点x1，x2，…，xn，以xi为中心构建方差为σi的高斯分布，并计算数据点xj关于xi的邻域概率pj|i。当点xj靠近xi时，其邻域概率pj|i较大；反之，当xj离xi很远时，其邻域概率pj|i则较小。定义如下：

在低维空间中，也使用条件概率来定义距离，高维数据点xi、xj映射到低维空间后对应yi、yj，则yj是yi邻域的条件概率qj|i为：

然后利用低维的条件概率分布Qi去拟合高维的条件概率分布Pi，采用Kullback-Leibler（K-L）散度来衡量两者之间的一致程度，从而确定低维分布与高维分布的相似性，最终通过最小化K-L散度实现降维。其目标函数定义为：

1.2K近邻算法

K近邻算法（K-NearestNeighbor，KNN）是一种经典的有监督学习方法，常用于解决分类问题。其原理是：在输入待分类数据时，将该数据的每个特征与训练集中样本数据的对应特征进行比较，随后选择训练集中前K个最相似的数据点，并根据这K个数据中出现次数最多的分类标签，确定待分类数据的类别。

在该研究中，首先采用t-SNE算法对数据集进行降维。然后，对降维后保留的特征构建特征矩阵。假设训练集中包含n个图像，则由这些图像构成的特征矩阵可表示为：

在（5）式中，Xn×l矩阵也称为特征空间X，n代表训练集中图像的个数，l表示特征的维度。当输入待分类的数据时，首先进行特征降维，即选择与训练集降维后的相同特征进行保留。并构成特征向量为：

Xj=（X"j1，Xj2，…，Xjl）（6）

则待分类数据与训练集中样本的距离定义为：

在（7）式中，当p=1时，称为曼哈顿距离；当p=2时，称为欧式距离，即：

2实验测试与结果分析

分别采用手写数字数据集、鸢尾花（iris）数据集进行实验。

2.1手写数字数据集

手写数字数据集包含1934个图像，涵盖数字0至9，每个数字约有200个样本。图像的尺寸为32像素×32像素，因此每个样本包含1024个特征变量。

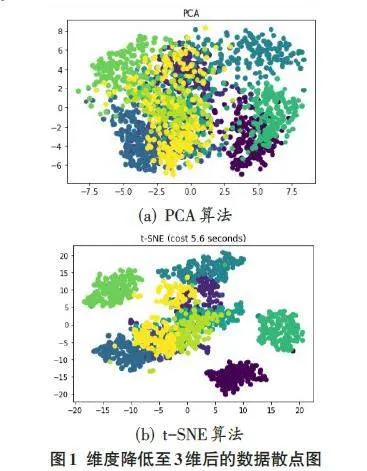
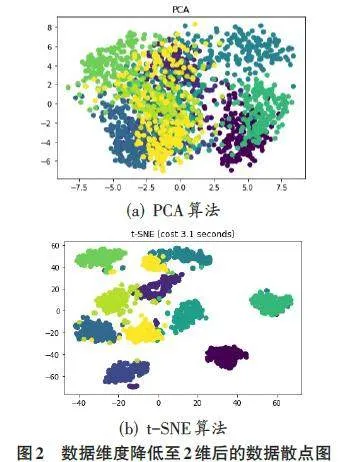
首先，分别采用主成分分析方法（PCA）和t-SNE算法对手写数字数据进行降维，其中PCA将数据降至3维，t-SNE将数据降至2维，降维结果如图1和图2所示。

由图1和图2可以看出，无论是将数据降至3维还是降至2维，使用PCA算法时数据分布较为集中，可分性较差；而使用t-SNE算法时，数据的可分性较高，且数据分布约形成10个簇，表明t-SNE算法的降维效果更优。此外，使用t-SNE算法将数据降至3维时所需时间为5.6秒，而降至2维时所需时间为3.1秒，这说明t-SNE算法在降维至更低维度时，计算所需时间更少。

接下来，将降维后的数据划分为训练集和测试集，采用KNN算法进行分类预测，并计算识别的准确率，结果如表1所示。

由表1可以看出，在手写数字数据集中，使用t-SNE算法降维后再结合KNN算法进行分类，分类准确率均在98%以上，比PCA算法高出约20%。此外，在降维至更低维度时，t-SNE算法的分类准确率下降较小，能够更好地保证数据分类的准确性。

2.2鸢尾花数据集

鸢尾花数据集共有150个样本，包含5个变量，其中4个为特征变量，分别是花萼长度（cm）、花萼宽度（cm）、花瓣长度（cm）和花瓣宽度（cm）；另1个为目标分类变量，表示花的类别。目标变量对应鸢尾属下的三个亚属，分别为山鸢尾（Iris-setosa）、变色鸢尾（Irisversicolor）和维吉尼亚鸢尾（Iris-virginica）。

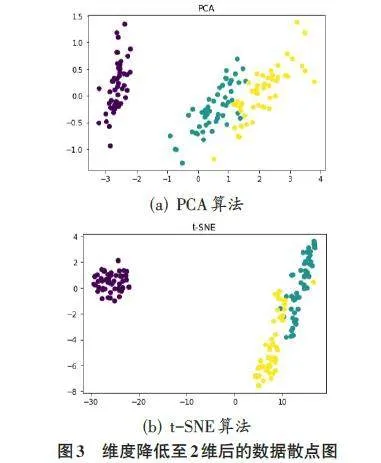
首先，分别采用主成分分析方法（PCA）和t-SNE算法对鸢尾花数据进行降维至2维，降维结果如图3所示。

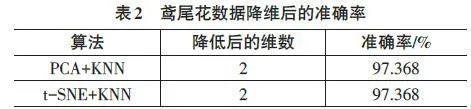
将降维后的数据划分为训练集和测试集，采用KNN算法进行分类预测，并计算分类识别的准确率，结果如表2所示。

由图3和表2的结果可以看出，在鸢尾花数据集中，两种算法降维后的数据点均具有较好的可分性，数据点集中为3类样本，且彼此较为独立。分类准确率均在97%以上，表明两种算法在鸢尾花数据集上均表现出较好的适应性。

3结束语

本文主要研究了基于t-SNE特征降维和K近邻的分类算法，分别采用PCA算法和t-SNE算法对特征数据进行降维，并对降维后的数据利用KNN算法进行分类预测。为了验证算法的适应性，分别在手写数字数据集和鸢尾花数据集上进行了实验。

实验结果表明，在手写数字数据集中，使用t-SNE算法降维后，数据的可分性较高，降维效果较好，分类准确率达到98%以上，比PCA算法高出约20%。此外，随着维度的降低，本算法在保证分类准确率的同时，还能显著缩短程序运行时间。在鸢尾花数据集中，两种算法的分类效果均较好，分类准确率均在97%以上。

综上所述，本文提出的基于t-SNE特征降维和K近邻的分类算法能够在降维幅度较大的情况下，仍保持较高的分类准确率，并且随着维度的降低，算法运行时间进一步缩短。此外，该算法对不同类型的数据集均表现出较高的适应性。

参考文献：

[1]褚治广，张兴，张青云，等.改进成分分析的差分隐私高维数据发布方法[J].计算机应用与软件，2023，40（10）：337-344.

[2]乔铭宇，陈旻杰，张琳那.基于低方差滤波算法的改进降维算法[J].现代计算机，2021，27（20）：56-59.

[3]王旭.基于高相关滤波算法的PSO-LSTM连铸坯质量预测模型[J].冶金与材料，2021，13（4）：5-7.

[4]谢凡，鲁昊，张翰林，等.基于主成分分析、聚类和BP神经网络的湍流MILD燃烧初始着火过程的分析[J].燃烧科学与技术，2023，29（6）：685-692.

[5]杨文锋，林德惠，曹宇，等.基于PCA-SVM的飞机蒙皮激光分层除漆LIBS在线监测研究[J].光谱学与光谱分析，2023，43（12）：3891-3898.

[6]王磊，张劲，叶秋炫.LDACS系统基于循环谱和残差神经网络的频谱感知方法[J].系统工程与电子技术，2024，46（9）：3231-3238.

[7]张楠，孟庆华，鲍春雨，等.脑卒中患者运动过程中动力学特征的智能预测[J].医用生物力学，2024，39（3）：489-496.

[8]赵淑欢，葛佳琦，梁晓林，等.改进加权投票的PCA-Net多特征融合SSFR[J].计算机仿真，2023，40（4）：223-230.

[9]彭艺，冯小虎，贾树泽，等.基于PCA-DNMFSC的卫星异常检测方法研究[J].计算机仿真，2023，40（1）：48-52，142.

[10]刘佳悦.基于LDA降维和BP神经网络的手写数字识别[J].信息与电脑（理论版），2023，35（14）：187-189，193.

[11]荀鹏，李娟，魏玉峰，等.坝肩岩体质量LDA-KNN分类模型[J].成都理工大学学报（自然科学版），2024，51（2）：281-290，302.

[12]靳文哲，吕文涛，郭庆，等.基于改进3E-LDA的织物图像分类算法[J].现代纺织技术，2024，32（6）：89-96.

[13]彭灿华，韦晓敏.基于LDA主题模型的多数据库主题词挖掘算法[J].计算机仿真，2023，40（8）：483-487.

[14]王静，王艳丽，孙士保，等.基于非平衡数据的LDA-BPNN信用评分模型[J].计算机仿真，2023，40（2）：303-308，414.

[15]边荣正，张鉴，周亮，等.面向复杂多流形高维数据的t-SNE降维方法[J].计算机辅助设计与图形学学报，2021，33（11）：1746-1754.

【通联编辑：唐一东】

基金项目：2021年度广东省重点建设学科科研能力提升项目（2021ZDJS120）；广东省普通高校类科研项目（2021KTSCX269）