袁家庄节制闸不同参数对水闸底板弯矩的影响

摘 要：水闸底板的受力情况会影响泄水建筑物的稳定性，本文以袁家庄节制闸工程的水闸底板为研究对象，建立有限元模型，分析在不同因素影响下的弯矩变化规律，并建立多元非线性回归模型，对其弯矩进行预测，得出结论：底板厚度会对底板地基的应力分布造成一定的影响，从而导致不同底板厚度的底板中心弯矩具有一定的差异性。当底板厚度较小时，改变底板厚度对底板中心弯矩的影响较大，随着底板厚度增加，底板中心弯矩受其底板厚度的影响较小。

关键词：水闸底板；弯矩；多元非线性回归

中图分类号：TV 65" " 文献标志码：A

水闸底板的受力情况会影响泄水建筑物的稳定性，目前，许多专家针对水闸底板的受力特性进行研究。

于正洋等[1]以某防洪水闸为研究对象，建立数值分析模型，分析在不同工况下的应力变化规律，并对其安全性进行评估。张宇等[2]基于有限单元法，对某软土地基水闸受力特性进行分析，研究土、水闸底板间的相互作用情况。明华军等[3]以某水电站水闸底板为研究对象，采用弹性地基梁法对其底板的受力情况进行分析，并研究不同参数对其底板内力的影响规律。陈敏等[4]以某水利枢纽为研究背景，采用计算机仿真方法，对其水闸底板的应力变化及位移规律进行分析，并根据研究结果，对该过程进行相关优化。张枝阳等[5]以某水闸底板为研究对象，采用有限单元法，分析不同工况下的沉降及应力变化规律，为相关工程提供参考。

1 工程概况

本研究以袁家庄节制闸工程为研究背景，本工程是一座集城区供水、农田灌溉、改善水环境、防洪蓄水于一体的综合性中型水利工程，闸址以上控制流域面积为648km2。水闸按20年一遇洪水设计，50年一遇洪水校核，闸门高4m，有效挡水高度为3.5m，闸前一次可拦蓄水量为105万m³，正常蓄水位为22.9m，设计洪水位为24.76m，相应泄量为886m³/s，校核水位为25.37m，相应泄量为1120m³/s。

2 研究方法

水闸底板的受力情况会影响泄水建筑物的稳定性，本研究以大坝泄水建筑物的水闸底板为研究对象，建立有限元模型，分析不同因素影响下的弯矩变化规律，数值模拟方案见表1。

3 水闸参数对底板弯矩的影响

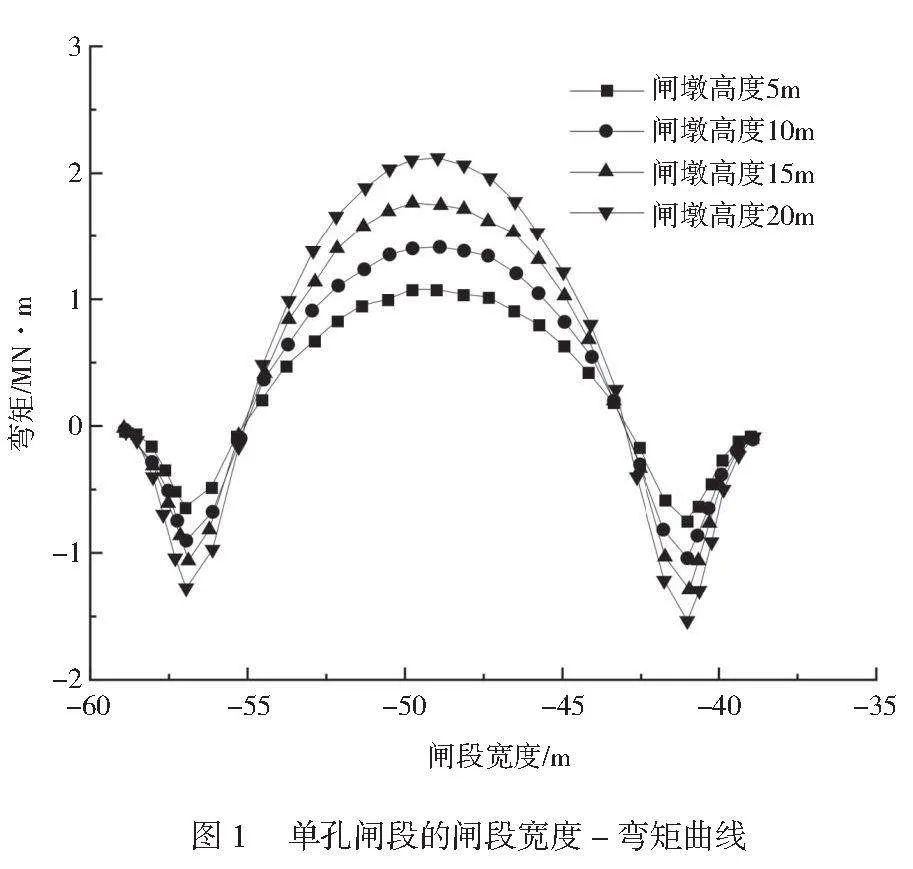
为分析水闸底板的受力规律，分别分析单孔、双孔闸板的弯矩分布情况，单孔闸段的闸段宽度（x）-弯矩曲线如图1所示。由图可知，当闸段宽度为-50 m时，其弯矩有最大值，说明位于水闸底板中部的弯矩值最大。不同闸墩高度的闸段宽度（x）-弯矩曲线变化趋势具有一致性，但是其弯矩值具有一定的差异性，当闸段宽度为-50 m（即水闸底板中部）时，闸墩高度与其所受的弯矩呈正相关关系，随着闸墩高度增加，其弯矩逐渐增加，其中，当闸墩高度为20 m时，其最大弯矩可达2.05 MN‧m。当位于水闸底板中部时，不同闸墩高度下的弯矩差异较大，当位于水闸底板边缘时，不同闸墩高度下的弯矩差异较小，说明当靠近底板中部时，闸墩高度对其弯矩的影响较大。

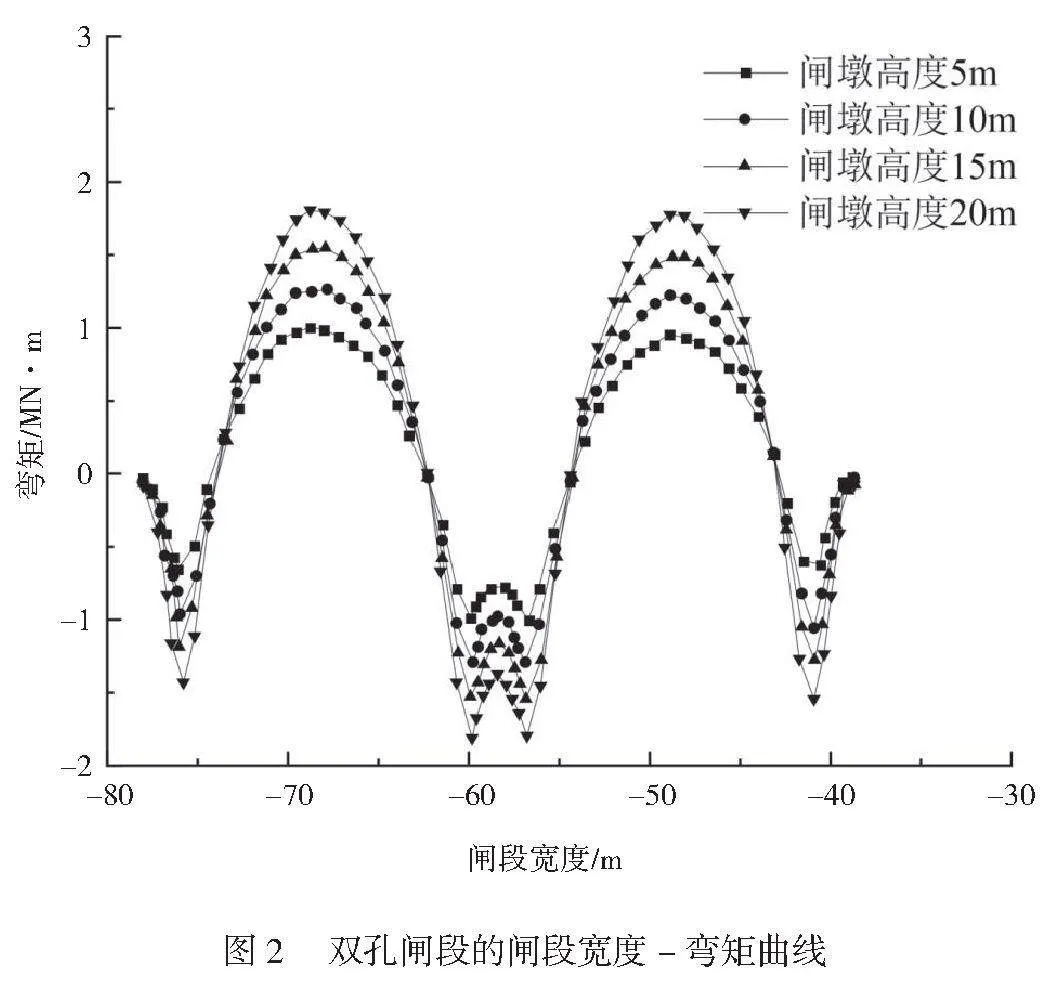
双孔闸段的闸段宽度（x）-弯矩曲线如图2所示。由图2可知，不同闸墩高度的弯矩变化趋势一致，其曲线近似双拱型，说明水闸底板的孔洞会影响其弯矩分布规律。双孔闸段的最大正弯矩与单孔闸段的差距较小，而其间的负弯矩差距较大，其最大负弯矩差值为0.74 MN‧m，说明当水闸底板为双孔时，其下部受拉的力学特性与单孔闸段差距较小，其受力差异主要体现在其底板上部受拉。随着闸墩高度增加，其弯矩逐渐增加，其中，当闸墩高度为20 m时，其最大弯矩可达到1.97MN‧m。

为分析底板厚度对水闸底板弯矩的影响，绘制底板厚度-弯矩曲线，如图3所示。由图3可知，底板厚度与底板中心弯矩间呈正相关关系，其所受弯矩随底板厚度增加而增加，底板厚度对底板地基的应力分布会造成一定的影响，因此导致不同底板厚度的底板中心弯矩具有一定的差异性。当底板厚度较小时，改变底板厚度对底板中心弯矩的影响较大，随着底板厚度增加，底板中心弯矩受其底板厚度的影响较小。

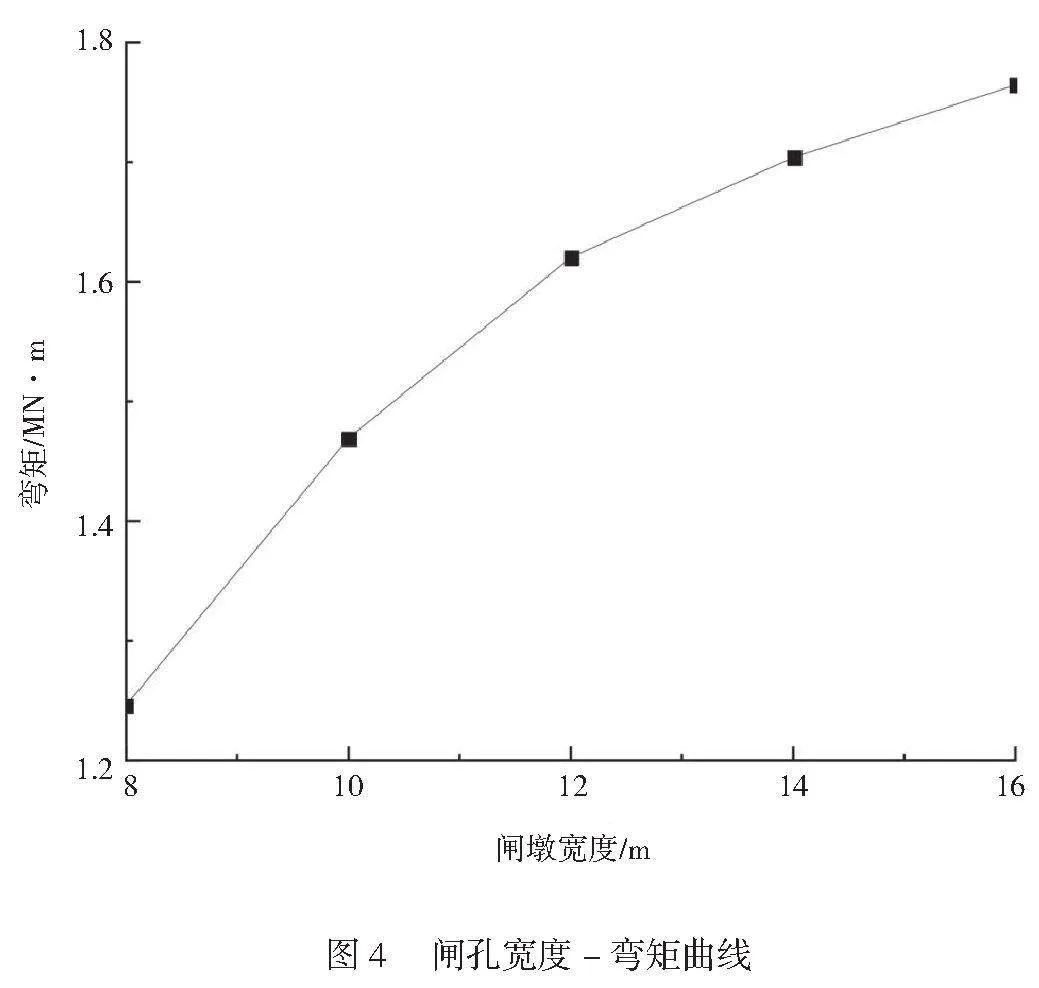
为分析闸孔宽度对水闸底板弯矩的影响，绘制其闸孔宽度-弯矩曲线，如图4所示。由图4可知，随着闸孔宽度增加，水闸底板的中心弯矩逐渐增加，当闸孔宽度较小时，底板中心弯矩的增长趋势较为显著，随着闸孔宽度增加，其增长趋势逐渐趋于平缓，当闸孔宽度发生改变时，水闸底板的尺寸也会随之变化，在底板尺寸与闸板宽度的影响下，水闸底板的中心弯矩逐渐增加。对比底板厚度对底板中心弯矩的影响可知，当改变底板厚度时，水闸底板中心最大弯矩为2.24 MN‧m，增量为1.74 MN‧m。当改变闸孔宽度时，水闸底板中心最大弯矩为1.76 MN‧m，增量为0.53 MN‧m，说明闸孔宽度对水闸底板中心弯矩的影响小于底板厚度。

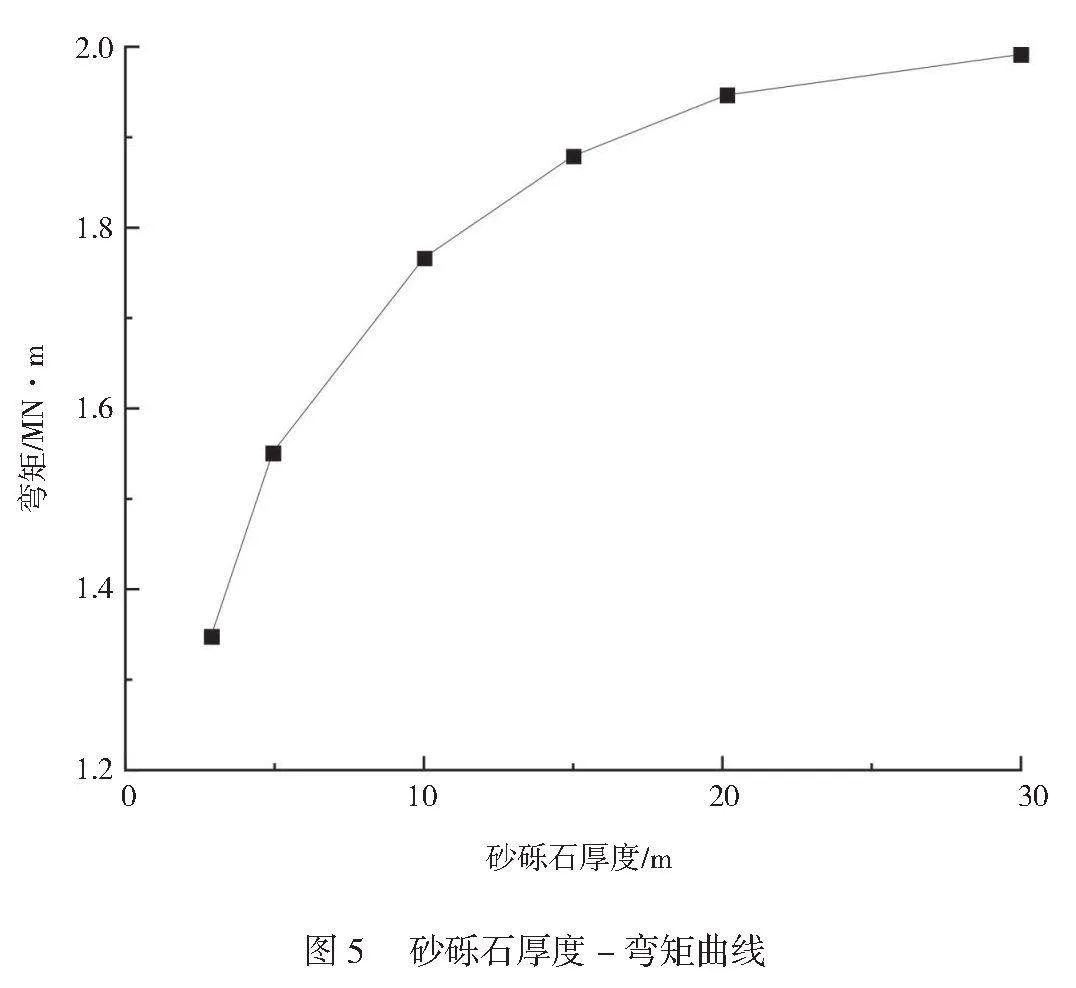
为分析砂砾石厚度对水闸底板弯矩的影响，绘制其砂砾石厚度-弯矩曲线，如图5所示。由图5可知，砂砾石厚度与水闸底板中心弯矩呈正相关关系，随着砂砾石厚度增加，水闸底板中心弯矩逐渐增加，当砂砾石厚度大于10 m时，其弯矩变化曲线变化趋势逐渐趋于平缓，说明当砂砾石基础较浅时，其对水闸底板弯矩的影响较大，随着基础深度增加，砂砾石厚度对底板弯矩的影响并不明显。当砂砾石厚度为30 m时，有最大底板中心弯矩，其值为1.98 MN‧m，增量为0.67 MN‧m，说明砂砾石厚度对水闸底板中心弯矩的影响程度大于闸孔宽度，小于底板厚度。

为分析闸墩高度对水闸底板弯矩的影响，绘制闸墩高度-弯矩曲线，如图6所示。

由图6可知，闸墩高度-弯矩曲线与上述参数的弯矩变化曲线具有一定的差异性，其水闸底板弯矩与其闸墩高度间呈线性正相关关系，说明随着闸墩高度变化，水闸中心弯矩的变化趋势较为平稳。当闸墩高度为20 m时，底板中心弯矩最大值为1.78 MN‧m，增量为0.76 MN‧m，对比上述参数可得，底板厚度对水闸底板中心弯矩的影响最大，其次为闸墩高度，再次为砂砾石厚度，闸孔宽度对底板中心弯矩的影响最小。

经过分析可得，底板厚度（x1）、闸墩高度（x2）、闸孔宽度（x3）以及砂砾石厚度（x4）对水闸底板的中心弯矩间存在相关关系，为分析以上因素对底板中心弯矩的影响，建立其多元非线性模型，如公式（1）所示。

y=k[x1ax2b（x3-c）x4d]" " " " " " " " " " " " " " " " " "（1）

式中：y为底板中心弯矩，MN‧m；a、b、c、d、k分别为回归参数。

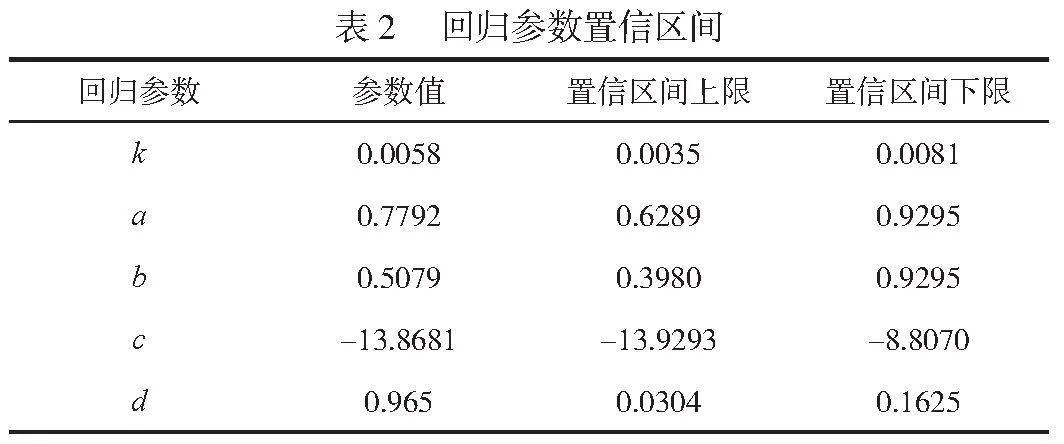
选取45组数据进行拟合，得出水闸底板中心弯矩模型，如公式（2）所示。该模型的回归参数置信区间见表2。

y=0.0058x10.7792x20.5079（x3+13.8681）x40.0965nbsp; " （2）

由表2可知，水闸底板中心弯矩的预测模型的置信曲线范围较小，说明以上参数均对底板弯矩有一定影响，对其进行回归分析，计算得出该模型的均方误差为0.0192，说明采用该模型预测的误差较小。

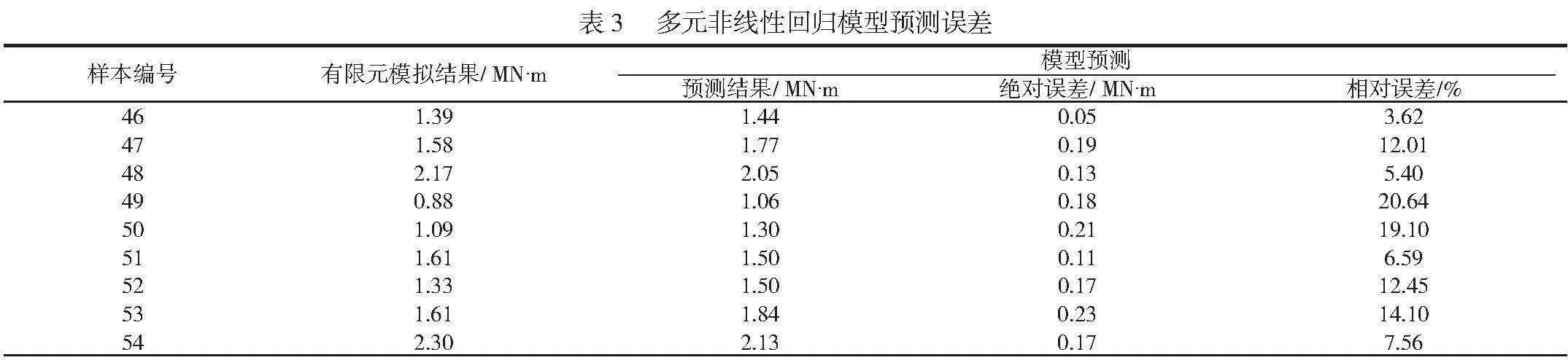
选取9组样本作为预测样本，将有限元模拟结果与预测结果进行对比，得出预测误差，以上9组样本的样本值与预测值的绝对误差与相对误差见表3。由表3可知，采用有限元模拟与模型预测得出的弯矩值差距较小，其中，样本46的误差最小，相对误差为3.62 %，样本49的误差最大，相对误差为20.64 %，9组样本的平均相对误差为9.1 %，说明采用多元非线性回归模型对水闸底板的弯矩值进行预测的准确率较高，可满足实际工程中的精度要求。

4 结论

本文依托袁家庄节制闸工程，通过数值模拟软件建立三维模型，以水闸底板弯矩为指标，对其进行敏感性分析，并结合多元非线性回归模型进行预测，得出以下结论。1）当闸段宽度为-50 m（即水闸底板中部）时，闸墩高度与其所受的弯矩呈正相关关系，随着闸墩高度增加，其弯矩逐渐增加。2）当底板厚度较小时，改变底板厚度对底板中心弯矩的影响较大，随着底板厚度增加，底板中心弯矩受其底板厚度的影响较小。

参考文献

[1]于正洋，苏静波，黄绍磊，等.基于三维有限元的异型底板水闸整体稳定性分析[J].河南科学，2022，40（2）：192-199.

[2]张宇，李同春，齐慧君.软土地基水闸底板有限元分析的桩基模拟方法[J].水利水电技术，2020，51（6）：65-71.

[3]明华军，张立勇，黄黎冰，等.基于弹性地基梁法的水闸底板内力影响因素分析[J].江西水利科技，2008（3）：161-163，167.

[4]陈敏，庄梦如，王明东，等.水利-交通联合枢纽工程中水闸底板设计优化分析研究[J].水利科学与寒区工程，2022，5（3）：19-23.

[5]张枝阳，程井，陈浩，等.软土地基上超长底板节制闸沉降及应力分析[J].三峡大学学报（自然科学版），2016，38（6）：31-34.