基于差分进化优化的随机森林产能预测

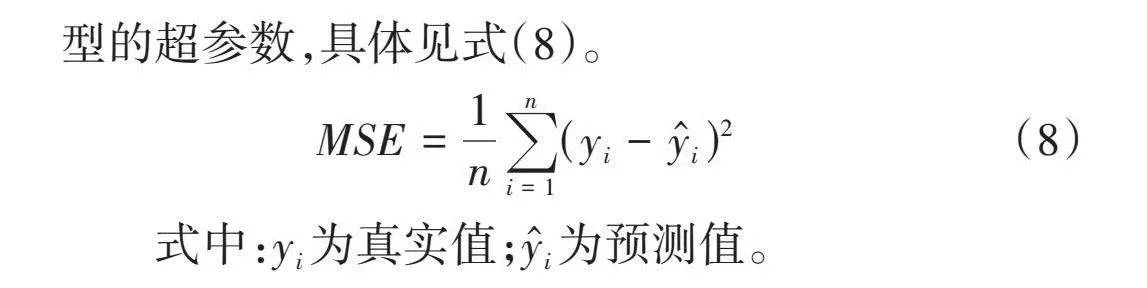
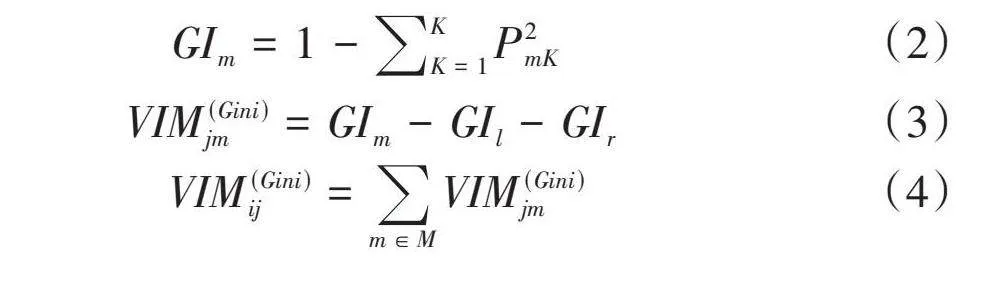
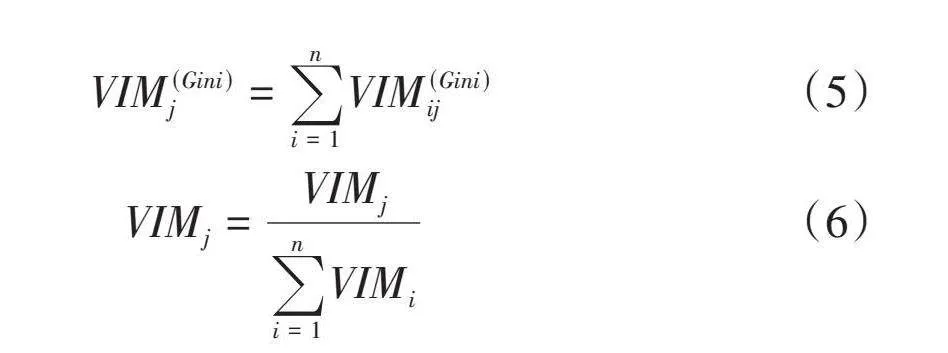
摘 要：【目的】为了解决传统的油藏产能预测方法存在考虑因素少、耗时长、计算过程复杂、在复杂地质条件下预测精度低等问题，有必要对基于差分进化优化的随机森林产能预测方法进行研究。【方法】采用机器学习的方法，建立基于差分进化算法优化的随机森林产能预测模型。以某油藏为例，根据油田实际开发情况，从地质、开发和工程等方面选择对产能影响比较大的6个因素，采用Person相关系数法分析各个影响因素之间的线性相关性，运用随机森林算法计算各个因素对产能的影响程度并进行主控因素分析。【结果】研究结果表明，孔隙度和含油饱和度之间的正相关性最强；对产能影响的程度从高到低分别为生产压差、射孔段厚度、渗透率、初始含油饱和度、油层有效厚度、孔隙度。支持向量机、多元线性回归、基于网格搜索优化的随机森林等方法中，采用基于差分进化优化的随机森林方法的预测精度最高。【结论】研究成果为复杂油藏产能预测提供了新的思路。

关键词：机器学习；产能预测；随机森林；差分进化

中图分类号：TE358.5 文献标志码：A 文章编号：1003-5168（2024）21-0032-06

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.21.007

Productivity Prediction Based on Random Forest Optimized by

Differential Evolution

MAO Jing CHEN Zhongxu LIU Jiayuan ZHAO Xing

（Tazhong Oil and Gas Management Department of Tarim Oilfield， Kuerle 841000， China）

Abstract： [Purposes] In order to solve the problems of traditional reservoir productivity prediction methods， such as less consideration， long time consuming， complicated calculation process， low prediction accuracy under complex geological conditions， it is necessary to study the random forest productivity prediction method based on random forest optimized by differential evolution. [Methods] This paper adopted machine learning approach and proposed a method of productivity prediction based on random forest optimized by differential evolution. A reservoir was selected as the example. According to the actual development situation of the oilfield， six factors which have greater impacts on productivity were selected from aspects of geology， development， and engineering. Person correlation coefficient method was used to calculate the linear correlation among influencing factors while random forest algorithm was applied to calculate the influence degree of each factor on productivity and analyze the main controlling factors.[Findings] The results showed that the positive linear correlation between porosity and initial oil saturation was the strongest. The degree of influence on productivity from high to low was producing pressure differential， perforation thickness， permeability， initial oil saturation， effective oil layer thickness and porosity. Compared with support vector machine， multiple linear regression and random forest optimized by grid search， random forest optimized by differential evolution has highest prediction accuracy.[Conclusions] This paper provided other theoretical method for predicting the productivity of complex reservoir.

Keywords： machine learning; productivity prediction; random forest; differential evolution

0 引言

油田产能的预测对整个油田开发至关重要，是各种方案的设计和调整的基础和依据，准确的产能预测不仅能够实现油田的高效合理开发，而且能够为将来新钻井进行合理的经济评估。传统的油藏产能预测方法对油气藏资料的全面性要求高。在建立数学模型时，复杂的公式推导计算量大、耗时长［1-2］，而且很难将各方面影响因素全部有效地结合在一起［3-5］。近年来，随着人工智能的迅猛发展，机器学习方法在油气田各领域得到了广泛应用，如岩性识别［6-9］、产能分析和预测［10-12］、压裂改造预测［13］、结垢预测［14］、沥青质沉积预测［15］、剩余油分布预测和注采参数优化［16-17］等。

在产能预测方面，机器学习方法可以对开发情况比较复杂的非常规油气藏进行有效、高精度的预测。常用的主要方法有核岭回归、多元线性回归［18］、支持向量机、随机森林、随机蕨、决策树、神经网络［19］等。林霞等［20］采用3种机器学习方法来预测油的产量，但是并没有综合考虑实际影响产能的地质、工程、开发等因素，只是简单地进行数据驱动。宋宣毅等［21］针对低渗油藏，采用随机森林方法对产能影响因素进行主控因素分析，并采用灰狼算法优化支持向量机来预测油井的初期产能，并与网格搜索优化的支持向量机、多元线性回归等方法进行了对比，该方法预测结果平均相对误差较小且提高了算法的计算效率，但因其样本数量过少，导致验证集整体拟合程度不高。机器学习算法虽然可以快速深入地挖掘影响因素与预测目标之间的联系，但算法中大量的参数如何进行合理的设置和调节仍是难题。目前，常用的方法将预测模型和优化算法结合在一起，然而由于优化算法本身的特性，不同的优化算法适用于不同的模型，因此合理选择优化算法也异常重要。针对上述问题，本研究提出一种结合差分进化优化算法的随机森林产能预测模型，采用该方法对随机森林的参数进行了优化，可有效解决其陷入局部最优的问题，大大提高了产能预测的准确率，缩短了计算时间。

1 影响产能的因素分析

研究单井产能影响因素对于单井乃至整个油藏的开发和调整具有重要意义。通过对影响产能的因素重要性进行程度评估，可以更好地帮助评估识别出影响因素对产能贡献的程度，进而从众多因素中分析出主控因素。对单井产能主控因素的分析，可以为老井接下来的开发进行合理有效的调整，最大程度提高单井产量，同时也为新井的钻探提供科学依据，以实现油田的高效益开发。

1.1 区块概况

某油藏全区面积为2.432 km2，总体南西—北东向展布，目的层储层物性好，共3层，均属于高孔高渗储层。其中目的层1储层平均孔隙度为26.23%，平均渗透率为500.13 mD。目的层2较目的层1储层物性好，平均孔隙度为29.56%，平均渗透率为700.58 mD。目的层3平均孔隙度为26.84%，平均渗透率为1 000.43 mD。油藏以注水开发方式为主，见水速度快。油藏岩石类型及岩性为组合发育有砾岩、砂砾岩、砂岩、粉砂岩、泥岩等岩石类型。

1.2 影响因素确定

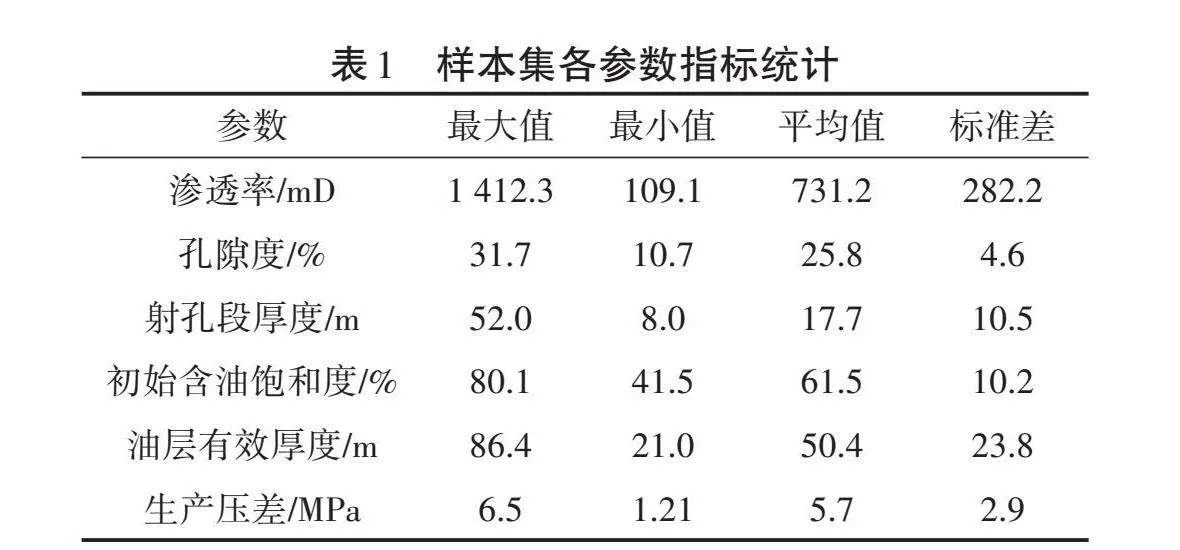
影响单井产能的因素众多，主要分为地质、开发、工程等3方面：①地质方面，如初始含油饱和度、孔隙度、油层渗透率、油层有效厚度等；②开发方面，如地层的压力系统、井网系统、井间连通情况等；③工程方面，如射孔工艺、压裂施工参数等。本研究以某砂岩油田为例，根据该油田实际生产开发情况，地质方面选择渗透率、孔隙度、初始含油饱和度、油层有效厚度等4个影响因素；开发方面由于该油田以衰竭式和注水开发方式为主，影响产能大小的主要因素为地层的压力系统，因此选择生产压差作为影响因素；工程方面考虑到未对该井进行压裂增产等措施，故选择有效射孔厚度作为影响因素。统计该油田45口生产井开井一年的平均日产油量，并选取了以上6个影响单井产量的因素作为特征值，建立了模型的样本集。通过上述方法对样本集数据进行处理，处理数据结果见表1，将样本集的80%作为训练集，20%作为验证集。

1.3 影响因素重要性分析

不同影响因素之间相互干扰情况以及对产能的敏感性各不相同。首先采用Person相关系数法分析两个不同因素之间的线性相关性，相关系数的变化范围为［-1，1］，正数代表正相关，即两个变量向相同的方向变化，其中一个变量增加，另一个

变量也增加；负相关则与正相关相反；0代表两个变量之间无线性相关性。相关系数的计算见式（1）。

[ρX1，X2=cov（X1，X2）δX1δX2] （1）

式中：cov为协方差；[δ]为标准差。

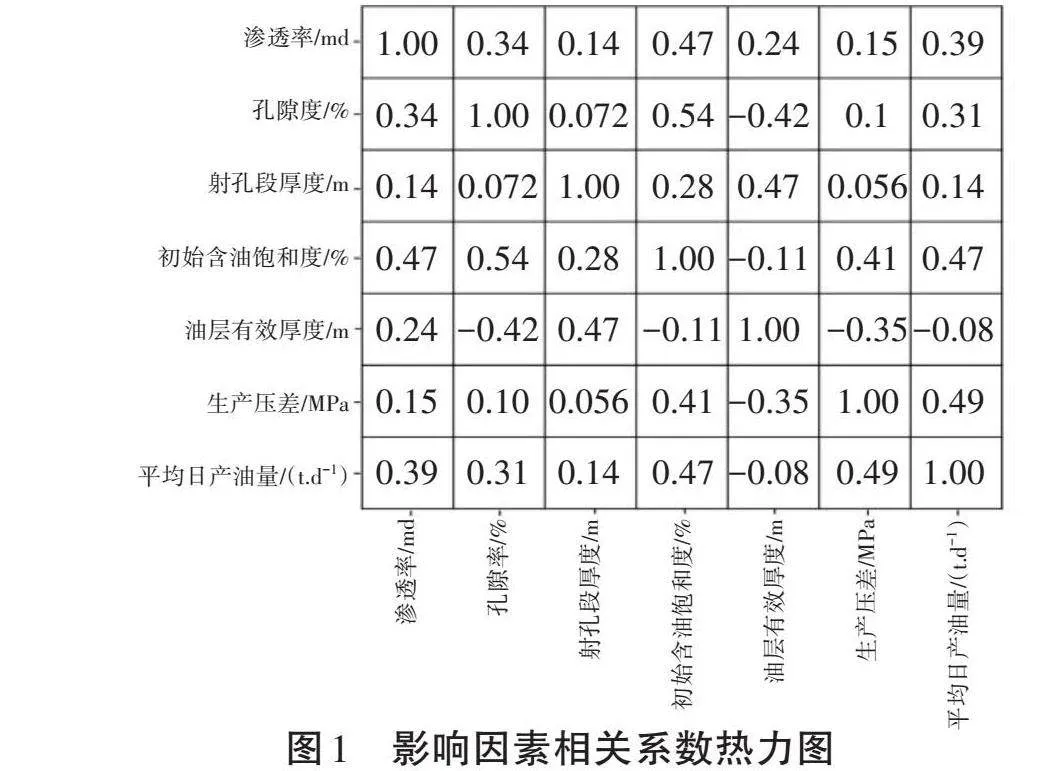
利用上述方法计算6个影响因素每两个之间以及各个影响因素与产量之间的相关系数，并将其绘成相关系数热力图如图1所示。由图1可知，不同影响因素之间，孔隙度和含油饱和度之间的正相关性最强，相关系数为0.54，因此二者对于原始地质储量的影响较大。油层有效厚度和孔隙度之间的负相关性最强，相关系数为-0.42。而在不同影响因素和产能之间，其相关性都比较弱，均低于0.5。由此可以推断，不同影响因素与产能之间不是简单的线性关系，且不是由某一个影响因素起决定性作用，是由所有因素共同作用。

因此，本研究采用随机森林算法具体计算每一个影响因素对产能的重要程度，并进行主控因素分析。其原理是评价每个特征在随机森林每一棵决策树上所做贡献的大小。贡献值的大小通常采用基尼指数GI作为评价指标来衡量，变量的重要性评分使用VIM来表示，随机森林中树的个数为n。影响因素重要程度的计算过程见式（2）至式（6）。

[GIm=1-K=1KP2mK] （2）

[VIM（Gini）jm=GIm-GIl-GIr] （3）

[VIM（Gini）ij=m∈MVIM（Gini）jm] （4）

[VIM（Gini）j=i=1nVIM（Gini）ij] （5）

[VIMj=VIMji=1nVIMi] （6）

以上式中：K为特征的类别；[Pmk]为节点m中类别K所占的比例；[VIM（Gini）jm]为节点m前后基尼指数的变化量；GIl、GIr分别为m节点分支后两个新节点的基尼指数；[VIM（Gini）ij]为特征Xj在第i棵决策树的重要程度；VIMj为Xj所有决策树的重要程度之和。根据上述原理，得到各个影响因素对产能的重要程度，见表2。

对以上结果进行分析可以得出，主控因素分别为生产压差、射孔段厚度、渗透率和初始含油饱和度，4个参数的各重要程度皆超过15%。因此对于老井而言，要控制好生产压差，避免生产压差过小，采油能力下降；对于新井而言，要打在初始含油饱和度比较高、渗透率比较大的区域，同时尽量增加射孔段数，投产后要及时控制好井底流压，从而最大程度地提高产油量，提高经济效益。

2 预测模型建立

2.1 随机森林回归原理

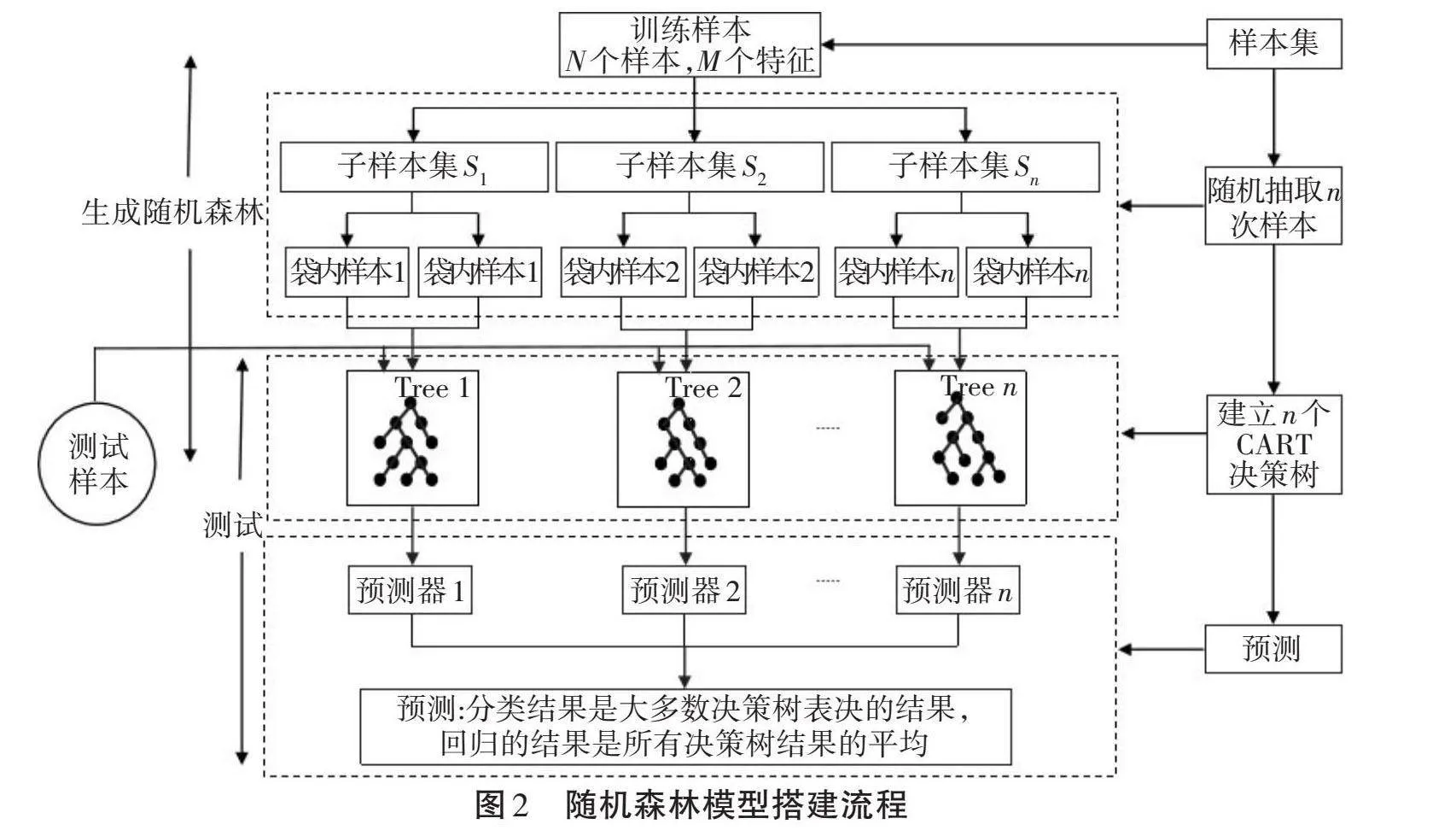
随机森林模型为基于Bagging算法的一种集成学习方法，由多个决策树集成而来。其既可以用来对数据进行分类，也可以用来回归，回归的结果为随机森林中每一棵决策树回归结果的平均值。其回归模型搭建流程如下。

①在大小为N的初始数据样本库中，以随机有放回的方式重复m次抽样，每次抽样得到n个数据，构建新的样本子集[S1，S2，S3，…，Sn]。

②将每个子样本集训练成一棵决策树，从所有特征中随机选择Q个，选出最优的节点进行分裂，从而将一个节点分裂为左右两个子节点。循环上述过程直至达到设定的终止条件，则停止分裂。

③对于分类问题，输出的结果是多数决策树表决的结果；对于回归问题，输出的结果是所有决策树预测结果的平均。具体的随机森林机器学习模型搭建的流程如图2所示。

2.2 建立DE-RF模型

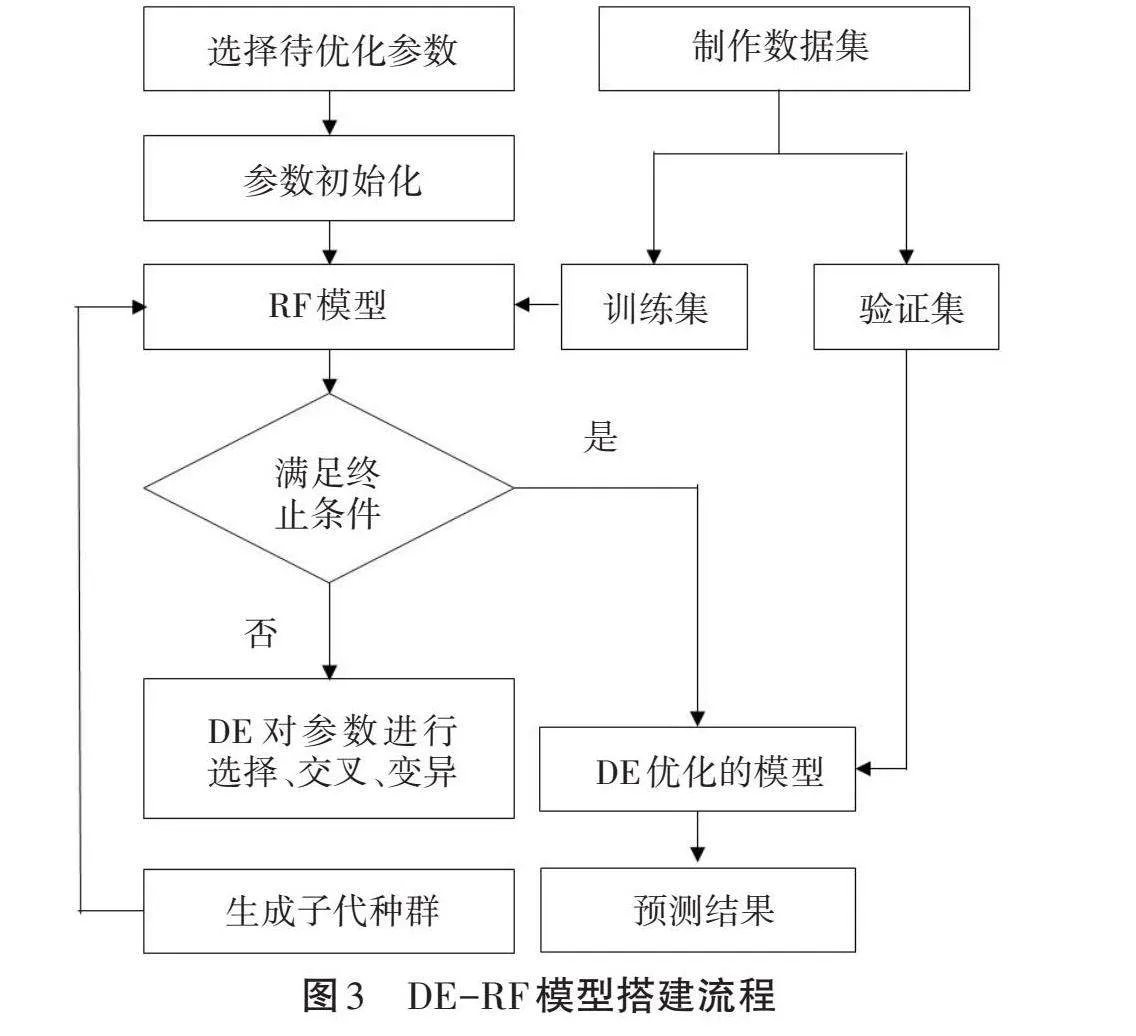
差分进化算法是在遗传算法及其他进化思想的基础上提出的。该算法可以有效降低操作和计算的复杂性，其专有的记忆能力可以根据目前的动态搜索情况，实现调整搜索的目的，具有极强的收敛能力和稳健性，且不用借助问题的特征信息，经常用于求解多维空间中整体最优解，故用来优化随机森林模型中的重要参数，从而建立一种新的基于差分进化优化模型超参数的随机森林回归模型（DE-RF）。该模型不仅解决了人为设置模型超参数速度慢和精度的问题，而且为随机森林模型与其他各种算法的融合提供了新的思路。DE-RF模型的产能预测详细流程如下。

①收集各类数据样本，前80%的数据为训练集，剩下20%的数据为验证集，对数据进行归一化以消除各数据由于数量级不一致对模型训练带来的影响，处理结果见式（7）。

[X'i=xi−xminxmax−xmin] （7）

式中：[xmin]为数据最小值；[xmax]为数据最大值。

②从模型中选择影响较大的5个参数分别为树的个数n、树的深度d、最大特征个数f、内部节点再划分所需的最少样本数s、叶子节点最小样本数l。然后，将选定的5个参数设为差分进化优化的变量，并确定其取值范围，对这些参数进行基于差分进化迭代（初始化、变异、交叉和选择），并将得到的参数取值代入随机森林模型，采用预测数据与实际数据的均方误差（MSE）作为目标函数并使其最小化。在达到迭代终止条件后输出MSE最小值情况下5个参数的取值作为用于产能预测随机森林模型的超参数，具体见式（8）。

[MSE=1ni=1n（yi-yi）2] （8）

式中：[yi]为真实值；[yi]为预测值。

按照上述步骤，DE-RF模型搭建流程如图3所示。

3 模型实例应用

以统计的45口生产井为例，将其中36口生产井作为训练集，9口生产井作为验证集，使用差分进化算法对随机森林模型中的树的个数n、最大特征值f、最大深度d、叶子节点最小样本数l、内部节点再划分所需的最少样本数s等5个参数进行优化。将差分进化算法中的缩放因子设为0.8，交叉概率设为0.2，迭代次数设为150，随机森林状态参数设为8。按照上述流程，最终得到基于差分进化优化的随机森林产能预测模型，优化的参数见表3。

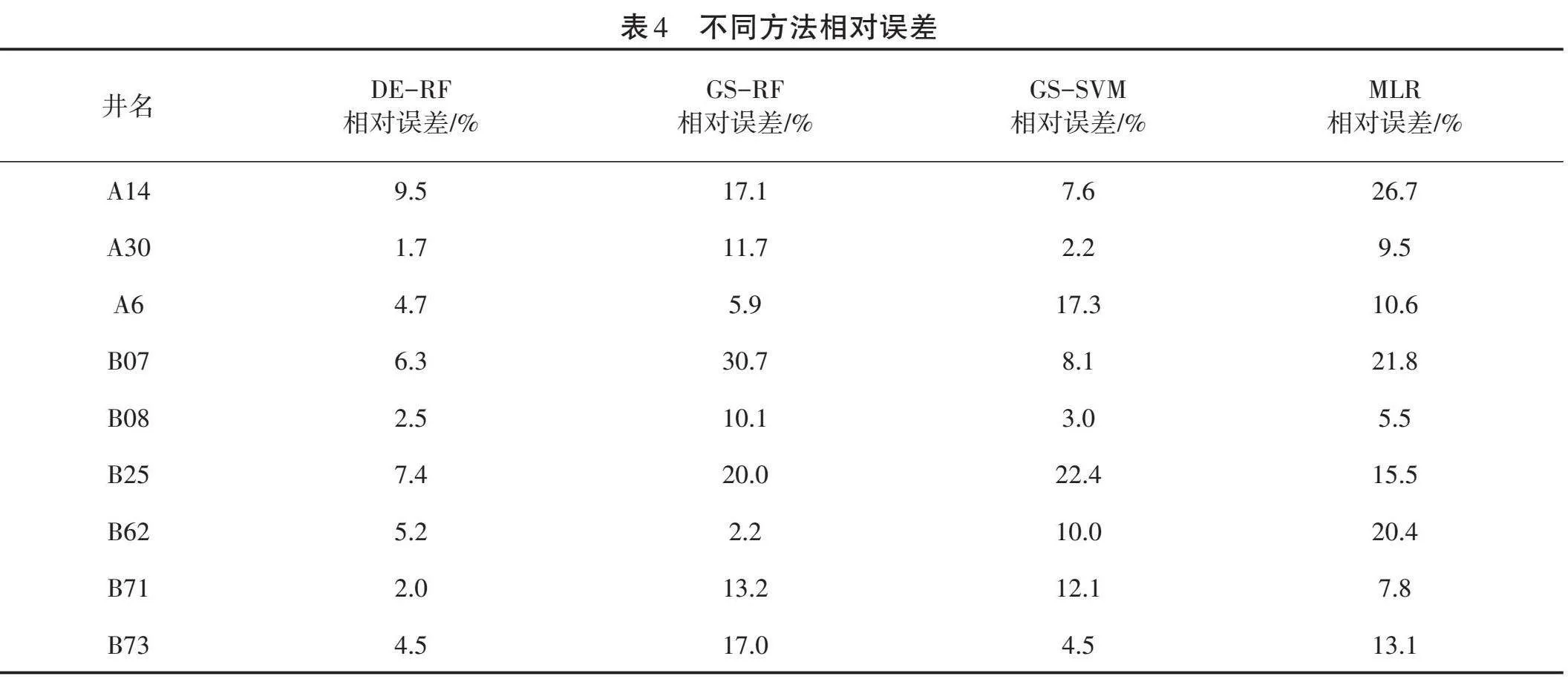
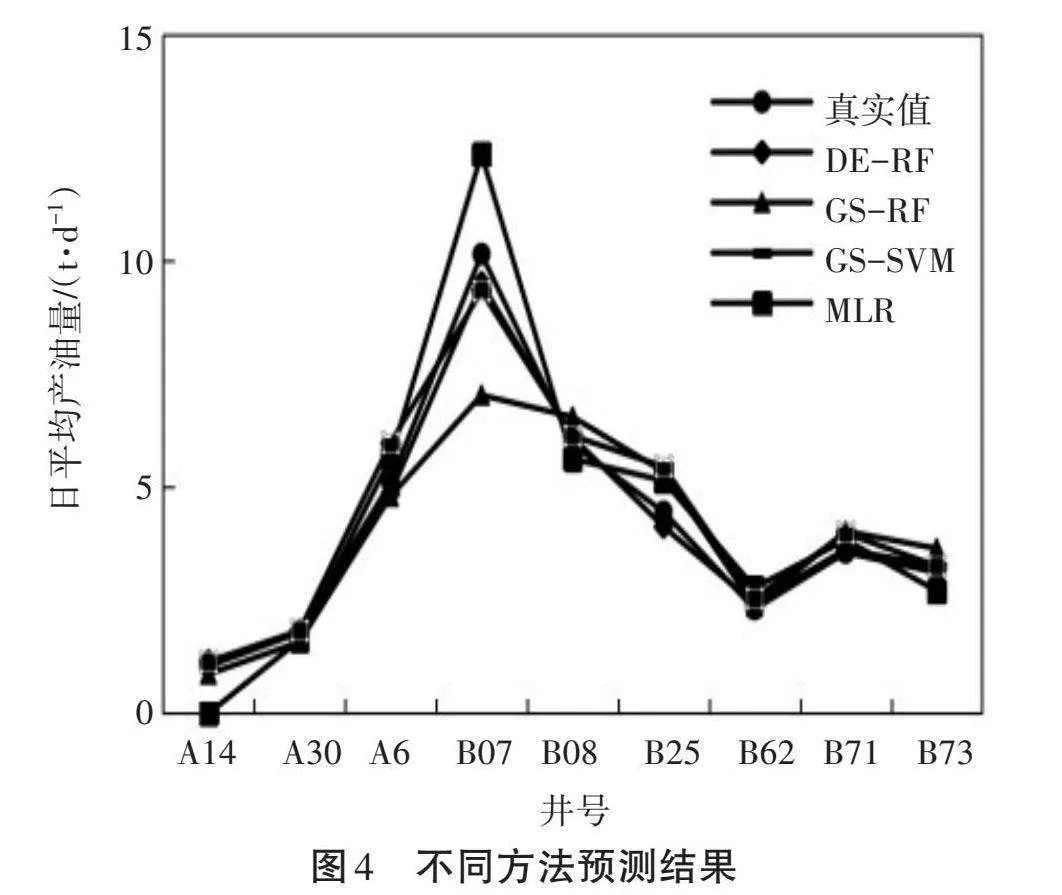
与此同时，本研究还采用基于网格搜索优化的随机森林模型（GS-RF）、基于网格搜索优化的支持向量机（GS-SVM）、多元线性回归（MLR）等3种方法进行了预测。不同方法预测验证集的结果如图4所示，相对误差见表4。

由表4可知，基于差分进化优化的随机森林模型，其验证集的预测结果相对误差均低于10%，模型的精度较高；基于网格搜索优化的随机森林模型只有两口井的相对误差小于10%，B07井的相对误差甚至超过了30%，平均误差为14.2%，误差较大的原因是采用网格搜索容易陷入局部优化；基于网格搜索优化的支持向量机模型的准确率不超过90%，这是由于支持向量机的计算量比较大，求解的是关于二次规划的问题，虽然经过了网格搜索优化，但适应性还是不高；多元线性回归方法的平均误差为14.54%。

4 结论

①采用随机森林方法对影响产能的6个因素进行重要程度分析得出，重要程度从大到小分别是生产压差、射孔段厚度、渗透率、初始含油饱和度、油层有效厚度、孔隙度。主控因素为生产压差、射孔段厚度、渗透率、初始含油饱和度，主控因素影响程度之和为93%。

②不同影响因素之间，孔隙度和含油饱和度之间的正相关性最强；不同影响因素与产能之间不是简单的线性关系，也不存在某一个起决定性作用的影响因素，产能是由所有因素共同作用的。

③ 基于差分进化优化随机森林模型将优化和预测结合一起，相较于其他模型，该模型的误差更小。本研究为油气田的产能预测提供了新的思路，具有重要意义。

参考文献：

［1］张意超，陈民锋，屈丹，等.X油田特低渗透油藏井网加密效果预测方法［J］.岩性油气藏， 2020， 32（1）：144-151.

［2］李金池，胡明毅，李忠诚，等.基于三维地质建模的复杂断块致密气藏产能预测［J］.断块油气田，2020，27（1）：69-73.

［3］熊健，邱桃，郭平，等.非线性渗流下低渗气藏压裂井产能评价［J］.石油钻探技术，2012，40（3）：92-96e93c355bdb30e7e5db0cfb6e7bf7aece.

［4］周德华，葛家理.应用等值渗流阻力法建立面积井网水平井产能方程［J］.石油实验地质，2004（6）：594-596.

［5］祝志敏，党勇杰，谢飞，等.分支水平井产能计算研究［J］.石油地质与工程， 2012，26（3）：82-84，119.

［6］JOBE T D， VITAL-BRAZIL E， KHAIT M. Geological feature prediction using image-based machine learning［J］. Petrophysics– The SPWLA Journal of Formation Evaluation and Reservoir Description， 2018， 59（6）：750-760.

［7］SILVA A A， LIMA NETO I A， MISSAGIA R M， et al. Artificial neural networks to support petrographic classification of carbonate-siliciclastic rocks using wellogs and textural information［J］.Journal of Applied Geophysic，2015，117：118-125.

［8］武中原，张欣，张春雷，等. 基于LSTM循环神经网络的岩性识别方法［J］.岩性油气藏，2021，33（3）：120-128.

［9］孙予舒，黄芸，梁婷，等.基于XGBoost算法的复杂碳酸盐岩岩性测井识别［J］.岩性油气藏， 2020， 32（4）：98-106.

［10］杨志成，刘月田，陈方园.改进的聚类法在水平井产能预测中的应用［J］.石油地质与工程，2009，23（5）：60-63.

［11］马文礼，李治平，高闯，等.页岩气井初期产能主控因素“Pearson-MIC”分析方法［J］.中国科技论文， 2018， 13（15）：1765-1771.

［12］钟仪华，张志银，朱海双.特高含水期油田产量预测新方法［J］.断块油气田，2011， 18（5）：641-644.

［13］纪磊，李菊花，肖佳林.随机森林算法在页岩气田多段压裂改造中的应用［J］.大庆石油地质与开发，2020， 39（6）：168-174.

［14］程翊珊，李治平，许龙飞，等 预测油层无机积垢的BP神经网络方法［J］.大庆石油地质与开发， 2021， 40（3）：84-93.

［15］吴君达，李治平，孙妍，等.基于最小二乘支持向量机的二氧化碳驱油沥青质沉积对储层伤害的动态分析［J］.科学技术与工程，2020， 20（24）：9856-9863.

［16］吴君达，李治平，孙妍，等. 基于神经网络的剩余油分布预测及注采参数优化［J］.油气地质与采收率，2020， 27（4）：85-93.

［17］王链，张亮，赖枫鹏，等.基于替代模型的油藏注采参数多目标优化设计［J］.科学技术与工程， 2019，19（26）：178-185.

［18］高明星.多元回归法预测低渗透油藏压后产能研究［J］.石化技术， 2019， 26（10）：371-372.

［19］王洪亮，穆龙新，时付更，等.基于循环神经网络的油田特高含水期产量预测方法［J］.石油勘探与开发，2020，47（5）：1009-1015.

［20］林霞，武博宇，王洪亮，等.基于机器学习的油田产量预测的方法比较［J］.信息系统工程，2019（8）：120-122.

［21］宋宣毅，刘月田，马晶，等.基于灰狼算法优化的支持向量机产能预测［J］.岩性油气藏，2020，32（2）：134-140.