用户型缆桥交换机中塑料卡扣的仿真分析与结构优化

摘 要：本文对用户型缆桥交换机的卡扣尺寸优化进行了仿真模拟研究。通过ANSYS Workbench建立计算模型，采用正交试验法，主要分析了卡钩厚度、卡钩长度、卡钩宽度、导入角、拆卸角、顶部厚度和配合深度共7个关键尺寸对2种评价指标的影响规律和主次关系。结果表明，卡钩长度、配合深度、导入角和拆卸角对装入力和拆卸力的影响较显著，其优化尺寸分别为7mm、25°、55°和0.8mm。基于对应力分布和受力分析的比较，和原卡扣相比，优化后卡扣的装入力和拆卸力更符合设计要求。

关键词：悬臂卡扣；有限元；正交试验；结构优化

中图分类号：TH 131 " " " " " " " " 文献标志码：A

用户型缆桥交换机为广电同轴网的主流设备[1]，产线有装配简易、维修员有拆卸方便的需求。如果卡扣偏紧，拆装力就会过大，会出现生产和维修不便、卡扣断裂等现象；如果卡扣偏松，运输和跌落时就容易脱钩。因此，在量产中确保卡扣的拆装合适、可靠已成为业内结构设计的关键技术之一。

在卡扣结构优化方面，柏秋阳等[2]为优化汽车内饰塑料卡扣配合，总结了孔径、厚度参数对连接性能的影响规律。雷恒等[3]对车门卡扣做了仿真分析，探讨了卡扣材料、瓣厚和角度对连接性能的影响。然而，不同外壳尺寸因素的数量和因素间主次关系各不相同，因此需要具体问题具体分析。

本文针对用户型缆桥交换机的卡扣，以最大装入力和最大拆卸力为评价指标，研究了卡钩厚度、卡钩长度、卡钩宽度、导入角、拆卸角、顶部厚度和配合深度对评价指标的影响和主次关系，优化了卡扣尺寸，为同行产品的开发提供了设计依据和应用参考。

1 分析模型

1.1 几何建模与关键参数

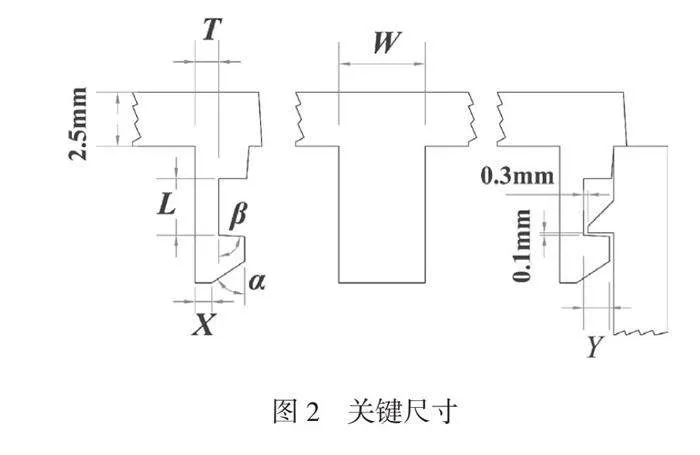
卡扣模型如图1所示，其外壳上盖与底壳通过箭头所示的8个卡扣实现装配。由于距离卡扣较远的壳体对计算结果影响较小且计算机资源有限，因此取单组卡扣为研究对象。取卡钩厚度T、卡钩长度L、卡钩宽度W、导入角α、拆卸角β、顶部厚度X和配合深度Y进行分析，关键尺寸如图2所示。

1.2 网格划分与边界条件

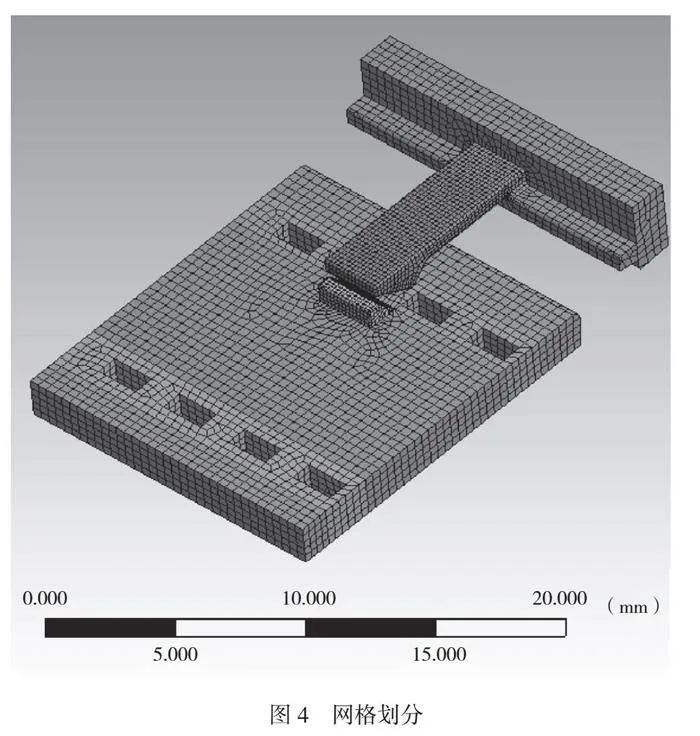
外壳上盖和底壳的材料为ABS塑料，取弹性模量2519MPa，泊松比0.39[4]。载荷与约束如图3所示，在卡扣母端上施加固定约束，在公端上施加位移约束。网格划分如图4所示，划分网格时，整体选用六面体网格，卡扣接触区域的加密单元为0.3mm，其余区域单元为1mm。计算域的网格数共17896个，节点70676个。为避免计算在棱边处不收敛，未注倒角取半径0.15mm。

分别将卡扣母端和公端设为接触面和目标面，接触类型为摩擦接触。鉴于两端材质相同，将Behavior（行为）设为Symmetric（对称）。选增强拉格朗日算法，开启Adjust to Touch（调整至接触），消除网格在接触初期的穿透。因为是面与面接触，所以高斯点探测法在积分点上计算的应力应变更准确，选On Gauss Point（在高斯点）。更新接触刚度，设为Each Iteration，Aggressive（每步迭代都强制更新）。

设定整个仿真时间为10s，前5s完成卡扣装入，后5a完成卡扣脱钩。开启子步设置，初始子步数选择200，最小子步数选择10，最大子步数为10000。求解器类型选用直接法（Direct），开启大变形选项。

1.3 评价指标

为了研究方便，将卡扣沿装配方向下行直到止位的过程中，所需的最大装入力定义为F1；将卡扣沿拆开方向上行直至脱钩的过程中，所需的最大拆卸力定义为F2。参考业内对卡扣拆装力的取值[4-5]，本文认为上盖和底壳配合的装入力范围宜为F1=24N～28N，拆卸力范围宜为F2=28N～32N。均分到8组卡扣，每组卡扣装入力为3N～3.5N，拆卸力为3.5N～4N。为便于评估效果，定义装配力评价指标P1=|F1-3.25|，拆卸力评价指标P2=|F2-3.75|。可见，评价指标P1和P2越小，装入力和拆卸力越接近预期目标。

2 结构优化

2.1 优化方法

单因素试验法和正交试验法[6]是卡扣结构优化的常见方法，前者侧重观察单因素的变化对评价指标的影响；后者侧重在因素较多、主次不明的情况下，通过少量试验掌握各因素、各水平间的内在关系。本文针对上述7个关键尺寸，将2种研究方法相结合，通过3个步骤进行分析。1）用正交试验法筛选出4个主要因素[6]。2）用单因素试验法，分析4个主要因素对评价指标的影响规律，缩小取值区间。3）用正交试验法，取四因素三水平进行分析。

2.2 七因素二水平研究

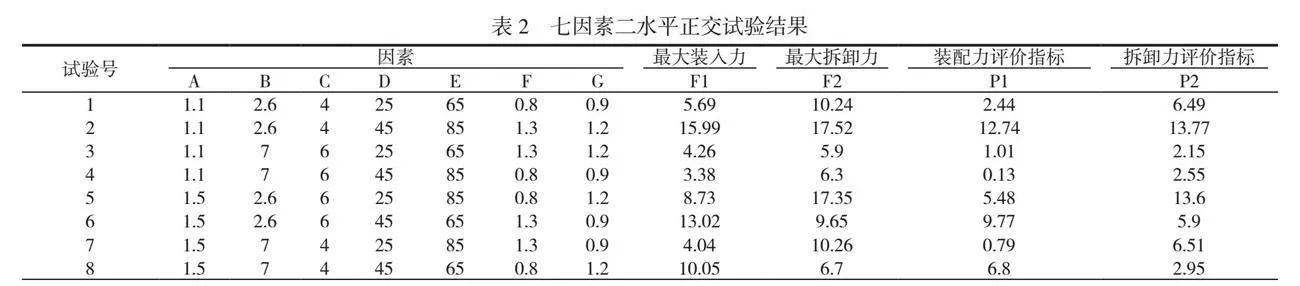
针对卡钩厚度T、卡钩长度L、卡钩宽度W、导入角α、拆卸角β、顶部厚度X和配合深度Y，将P1和P2分别作为装入力和拆卸力的评价指标，选用正交试验表L8（27）。因素水平设置见表1。

对表1方案进行仿真分析，结果见表2。对表2进行极差分析，结果见表3、表4。

在表3中，K1为某一个因素下，第一个水平的最大装入力F1之和；K2为第二个水平的最大装入力F1之和。同理可知，K3为某一个因素下，第一个水平的最大拆卸力F1之和；K4为第二个水平的最大拆卸力F1之和。对于每个水平对评价指标的影响强弱，可比较K值大小，K值越小，表示其对应的水平越接近设计目标。极差R1为K1和K2中较大值和较小值的差，同理，极差R2为K3和K4中较大值和较小值的差，该值越大，表示这个因素对评价指标的影响越大。

如果以装配力评价指标P1为准，可得7个因素对评价指标的影响从大到小依次为B、D、G、F、A、C、E。

如果以拆卸力评价指标P2为准，这7个因素对评价指标的影响从大到小依次为B、E、G、C、A、D、F。

由于因素D（导入角α）对装入过程影响较大，而因素E（拆卸角β）对脱钩过程影响较大。因此综合考虑后，决定4个主要因素为卡钩长度L、配合深度Y、导入角α和拆卸角β。

2.3 单因素分析

对某个单因素模型，随着一个主因素变化，其余3个主因素均为定值，取值见表4。

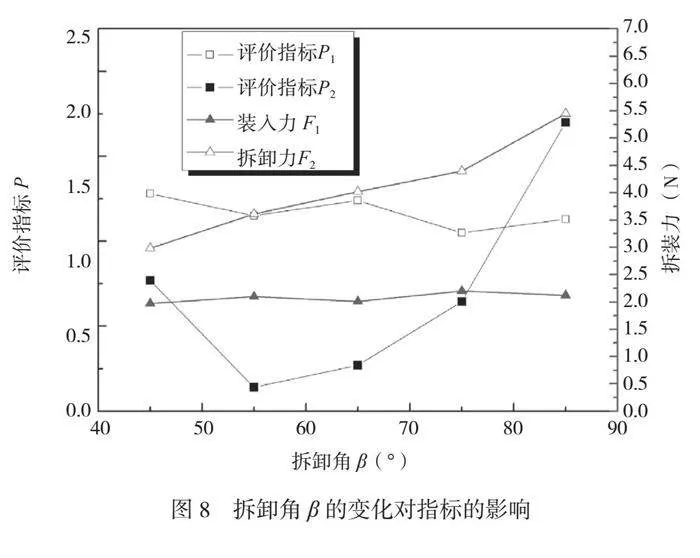
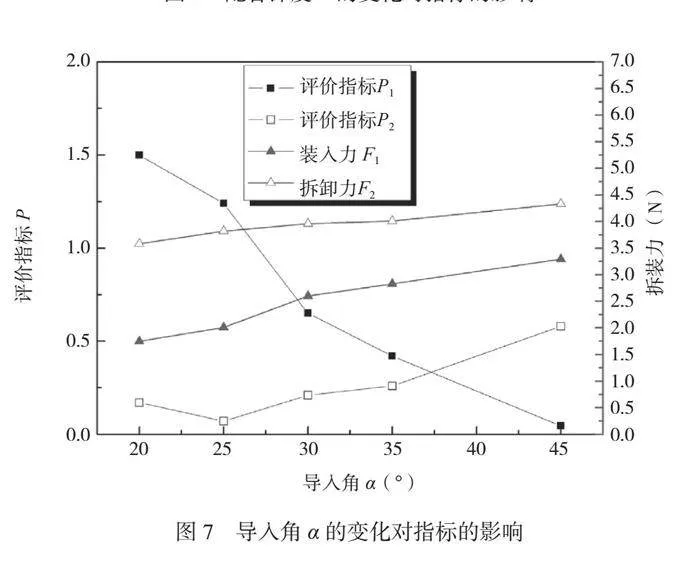
卡钩长度L、配合深度Y、导入角α和拆卸角β4个因素对2种评价指标的影响分别如图5～图8所示。

由图5可知，当卡钩长度L增大，最大装入力F1和最大拆卸力F2均逐渐递减。原因是卡钩长度越长，垂直于卡钩面上使卡扣偏斜的最大偏斜力越大，而最大拆装力和最大偏斜力存在正比关系[6]。评价指标P1和P2均呈先降、后升的趋势，因此卡钩长度在极小值点5mm～7mm。

由图6可知，随着配合深度Y增大，卡钩上最大偏斜力递增，导致最大拆装力也递增，于是最大装入力F1和最大拆卸力F2均呈上升趋势。根据评价指标P1，0.8mm为较优解。根据评价指标P2，该值随配合深度Y增加而递减，1.3mm为较优解。综合考虑，配合深度Y取0.8mm～1.3mm。

由图7可知，随着导入角α从20°增至45°，最大装入力F1从1.75N增至3.3N，可见导入角越大，最大装入力也随之增大。原因是导入角越大，垂直于卡钩面上使卡扣偏斜的最大偏斜力越大，最大装入力与之成正比[7]，因此呈递增趋势。而最大拆卸力F2较平缓，为3.58N～4.33N，可见导入角对其影响效果较小。再观察评价指标P1和P2，虽然最大装入力F1在45°时更接近设计目标，但最大拆卸力F2在25°时更优。因此，综合考虑，导入角α取25°～45°。

由图8可知，随着拆卸角β从45°增至85°，最大拆卸力F2逐渐递增。原因是拆卸角越大，卡钩上的最大偏斜力递增，最大拆卸力也随之呈递增趋势。而最大装入力F1变化不显著，为1.97N～2.2N，可见拆卸角对其影响较小。综合考虑评价指标P1和P2，拆卸角β取55°～75°。

2.4 四因素三水平正交试验

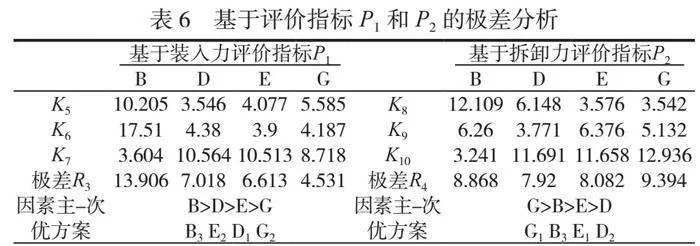
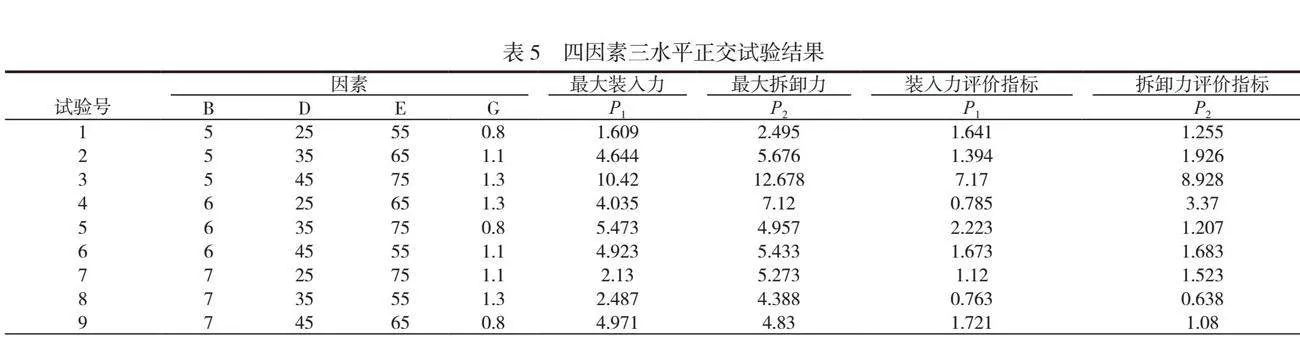
针对卡钩长度L、导入角α、拆卸角β和配合深度Y，选正交试验表L9（34）。次要因素为卡钩厚度T=1.1mm，卡钩宽度W=4mm，端面厚度X=0.8mm。四因素三水平正交试验结果和极差分析见表5、表6。

对于因素B（卡钩长度L），林杨明[7]总结了卡钩长度宜取5～10倍壁厚，因此本例取7mm。

对于因素D（导入角α），林杨明[7]总结了导入角宜取25°～35°。本研究中，导入角α主要影响装入过程，因此以指标因素P1结果为先，取25°。

对于因素E（拆卸角β），一般在30°～60°适宜正常脱钩[7]。在本文中，拆卸角β主要影响脱钩过程，因此以指标因素P2结果为先，取55°。

因素G（配合深度Y）在脱钩过程中为第一影响因素，而在装入过程中它只是第四影响因素，因此以指标因素P2结果为先，取0.8mm。

3 改良前/后的仿真对比

3.1 临界状态云图

在卡扣的装入和拆卸过程中，最大装入力和最大拆卸力这2个瞬间为关键的临界状态。观察原卡扣和优化后的卡扣在同一临界状态下的应力分布、最大装入力和最大拆卸力，以检验优化效果。

对于ABS的力学性能，林微等根据ABS材料在不同温度下的屈服强度和断裂伸长率的变化趋势，取屈服强度为49.94MPa，安全系数n为1.5[8]，根据[σ]=σe/n，得许用应力[σ]为33.3MPa。

在原卡扣的装入过程中，当装入力达到最大值19.45N时，卡钩上的应力云图如图9所示。此时，卡钩根部应力较集中，大多处于47.91MPa～54.75MPa，局部最大应力值为68.44MPa，大于许用应力33.3MPa，不满足设计目标。

在原卡扣的拆卸过程中，当拆卸力达到最大值12.99N时，卡钩上的应力云图如图10所示。此时，卡钩根部应力较集中，为99.34MPa～113.53MPa，最大应力值为141.91MPa，远超屈服强度49.94MPa，卡钩将断裂。应力最大值在卡钩根部边缘某一点的现象源于原卡钩根部为直角，未做圆角过渡，因此该处应力值骤增。

在新卡扣的装入过程中，当装入力达到最大值3.148N时，卡钩上的应力云图如图11所示。此时，应力最大值为31.5MPa，与原卡扣相比降低了54%，并小于许用应力33.3MPa，满足设计要求。此外，由于卡钩根部做了半径为0.5mm的圆角过渡，因此应力均匀分布在曲面上，与原卡扣集中于部分棱边和棱角相比，可靠性更高。

在新卡扣的拆卸过程中，当拆卸力达到最大值4.064N时，卡钩上的应力云图如图12所示。此时应力最大值为28.43MPa，与原卡扣相比降低了80%，并小于许用应力33.3MPa。此时，由于卡钩根部做了半径为0.5mm的圆角过渡，因此该处最大应力分布比原卡扣均匀，避免了原卡扣应力集中于一点的现象。可见在后续改模时，根部做适当的圆角过渡很有必要。

3.2 力与时间曲线对比

在原卡扣和新卡扣从装入拆卸的过程中，装入力、拆卸力随时间变化的曲线如图13所示。可见两者在先装入、后拆卸的10s内，卡扣上须施加的装入力和拆卸力呈现先增、后减的趋势。原卡扣上的最大装入力和最大拆卸力分别为-19.452N和12.986N，偏离预期目标较多。而优化后新卡扣上的最大装入力和最大拆卸力分别为-3.147N和4.062N，更贴近上文制定的拆装力标准F1和F2，可实现设计目标。

3.3 原卡扣设计缺陷及失效原因

经过上述研究，可知原卡扣失效的原因如下。1）原卡钩长度仅为2.6mm，而料厚为1.1mm，两者比值仅为2.36，偏离了林杨明[7]关于卡钩长度宜取料厚的5～7倍的结论，因此当卡钩发生相同形变时，原卡扣比新卡扣产生的偏斜力更大，拆装力也相应增大，导致拆装费劲。2）原卡钩拆卸角为90°，导致拆卸时根部应力超过材料的屈服强度，因此维修时常有卡钩断裂。3）原卡钩的顶部厚度X设计为1.3mm，超过了卡钩的厚度1.1mm，与林杨明[7]关于卡钩顶部厚度应小于卡钩厚度的结论不符，导致装入过程受阻较大，因此生产时常出现装配不顺畅的现象。

4 结论

本文对用户型缆桥交换机的卡扣尺寸优化进行了仿真研究，主要分析了7个关键尺寸对2种评价指标的影响规律和主次关系。所得结论如下。1）在卡钩装入过程中，影响程度从大到小依次是卡扣长度L、导入角α、拆卸角β和配合深度Y。在卡钩拆卸过程中，影响程度从大到小依次是配合深度Y、卡钩长度L、拆卸角β和导入角α。2）本款用户型缆桥交换机的卡钩优尺寸为卡钩厚度T=4mm、卡钩长度L=7mm、卡钩宽度W=4mm、导入角α=25°、拆卸角β=55°、顶部厚度X=0.8mm和配合深度Y=0.8mm。比较优化前、后，最大装入力和最大拆卸力均得到了改善，实现了预期目标。

参考文献

[1]茹伟光，王正军，倪晨鸣.C-HPAV在NGB接入网中的应用[J].电视技术，2013，37（20）：34-37.

[2]柏秋阳，王辉，郝旭飞，等.汽车内饰塑料卡扣配合结构设计研究[J].塑料工业，2015，43（9）：50-53，56.

[3]雷恒，郭鹏程，林启权，等.卡扣设计参数对连接性能的影响分析[J].机械设计与研究，2018，34（6）：163-167.

[4]纪海慧.Ansys Workbench在卡扣装配分析中的应用[J].现代制造工程，2008（8）：48-49，131.

[5]吴礼红，马腾，姚思捷，等.墙壁开关按钮卡扣的扣合量对脱扣力的影响研究[J].日用电器，2022（6）：74-78.

[6]于海华.悬臂钩卡扣装配有限元分析及优化设计[D].南京：南京理工大学，2009.

[7]林杨明.塑料制品悬臂卡扣连接件设计方法的研究[D].哈尔滨：哈尔滨工业大学，2009.

[8]单辉祖.材料力学（I）[M].北京：高等教育出版社，2006.