火电厂热能动力设备轴承同步伺服控制方法

摘 要：为增强轴承的旋转位置和速度控制精度，本文研究火电厂热能动力设备轴承同步伺服控制方法。对采集的异常数据进行预处理，得出谱峭度最大值，运用滤波器进行降噪处理。采用时域分析方法提取振动信号特征参数。设计轴承转动的同步控制系统，将轴承转子各自由度为控制目标。引入神经元，提升控制系统的自适应性，运用PID控制器进行控制。通过阻尼系数反映超调的抑制程度，修正阻尼函数，实现控制器的伺服控制。试验结果表明，使用该方法进行精确控制仅需0.06s，轴承转速为28r/min以内，结果符合预期，取得了良好的控制效果。

关键词：火电厂；热能动力设备；轴承；伺服控制

中图分类号：TM 383 " " " " " 文献标志码：A

轴承同步伺服控制是火电厂热能动力设备中的重要技术，通过精确的轴承同步伺服控制，可以减少设备运行过程中的能量损失，提高设备的运行效率，有助于降低能源消耗，提高火电厂的发电效率，还有助于减少设备故障和维修成本，提高设备的可靠性和稳定性。采用先进的轴承控制算法和技术，需要实时监测设备的运行状态并进行调整，以提高控制的实时性。因此，火电厂热能动力设备轴承同步伺服控制方法具有能提高设备运行效率、增强设备稳定性、适应性强和实时性好等优点，对提高火电厂的发电效率和降低能源消耗具有重要意义。

目前，传统的控制方法对不同工况和不同设备型号的适应性较差，需要针对不同的设备进行参数调整和优化，增加了维护和调试的难度[1]，因此本文研究了火电厂热能动力设备轴承同步伺服控制方法。

1 轴承同步伺服控制

1.1 火电厂热能动力设备轴承异常特征提取

使用振动传感器采集轴承振动信号数据，采样率设置为10kHz。根据采集的火电厂热能动力设备轴承信号数据提取异常特征进行同步伺服控制。利用谱分析法对采集的异常数据进行预处理[2]。运用谱峭来提升谱分析的频率分辨率，从而提升异常信号的识别效果。对非平稳过程分解，所得谱峭度信号的表达式如公式（1）所示。

y（t）=∫ej2πtH（t，f）dx （1）

式中：H（t，f）为原始信号；y（t）为时间t时的复包络；e为白噪声。

通常平稳高斯过程中的谱峭度为0，通过设计滤波器来增加信号中的冲击成分，对频率分辨率进行控制。带通滤波器如公式（2）所示。

（2）

式中：H（t）为滤波信号；f0为中心频率；Q为品质因数，决定了滤波器的带宽。

在给定的频率范围内，通过遍历中心频率f0和品质因数Q，计算每个组合下的谱峭度值，进而找到使谱峭度最大的中心频率和品质因数。根据找到的每个频段下的谱峭度值绘制一个二维彩色图像。颜色的明暗表示当前频段下的谱峭度值，可直观地观察到谱峭度的分布。将找到的最优中心频率和品质因数作为滤波器的参数，对原始信号进行滤波处理。处理后的信号所含的噪声成分更少，从而达到了降噪的目的。

运用时域分析的方法对振动信号进行时域波形分析，获得振动信号中的有用信息[3]，有效值特征的均值计算方法如公式（3）所示。

（3）

式中：N为分布特性的数值统计量；xi为脉冲因子。

通过特征计算公式进行特征参数提取，对于不同信号，需要灵活调整参数来获得差异化更大的特征参数。同时，当轴承故障时，会出现信号缺失的问题，将轴承正常工况下的数据作为输入数据，向轴承异常信号进行映射，加入轴承异常时的特性，能够补充完成信号特征，获得更真实的异常信号。以上过程应用频域插值法实现，具体过程如下。

使用傅里叶变换方法将时域信号转换到频域，生成频谱图，表示振动信号在不同频率上的能量分布。在频域上可观察到频谱的峰值、波峰和波谷等特征。通过分析正常工况下的频谱特征，确定信号的主要频率成分和幅值范围。再根据正常工况下的频谱特征确定信号缺失部分的频域数据，并进行线性插值处理，根据缺失数据点周围已有数据的频谱特征进行插值计算。

假设需要补充的缺失数据点位于频谱上2个已知频率点间，并且这2个频率点具有已知能量值，分别为f1和f2。设缺失数据点位于这2个频率点间的相对位置为L（范围为0～1），可以采用线性插值的方法计算缺失数据点的频谱能量，如公式（4）所示。

Emissing=E1+L（E2-E1） （4）

式中：Emissing为需要补充的缺失数据点的频域能量值，E1、E2分别为已知频率点处的能量值。

公式（4）表示在2个已知频率点的能量值间，根据其线性关系和根据位置比例L进行插值。通过线性插值对缺失数据点进行估计和补充，保持频域特征的连续性和一致性。

将插值后的频域数据进行反变换，转换回时域。这样，缺失部分的信号数据恢复为完整的异常信号。

上述过程将轴承正常工况下的数据作为输入数据并向轴承异常信号进行映射，通过加入轴承异常时的特性，对信号进行了补充和修复，获得了更真实的异常信号。

1.2 轴承转动模糊整定伺服控制

设计轴承转动的模糊整定伺服控制系统[4]。设定n维非线性动态系统，定义系统状态变量的函数为ψ（c，t），根据控制目标要求进行选择。对于多个控制输出的系统，需要定义n+1个宏变量。运用同步控制系统进行目标控制前，需要在有限时间内从初始状态开始收敛，使流形趋向被控系统的平衡点。用动态方程描述流形收敛的过程，如公式（5）所示。

Tψ+ψ=0 （5）

式中：T为设计参数；ψ为系统的流形。

由于宏变量是状态变量的函数，因此对函数进行求导可以得到控制量解。在控制过程中，系统将从初始状态趋近流形ψ=0，并一直保此状态。由此可提升控制系统的稳定性，使系统能在流形收敛过程中找到平衡点。

对于轴承转子系统，通常使用动力学方程来描述其动态行为。转子的运动状态由位移、速度和加速度等参数决定，并通过公式（6）来建立系统的数学模型。

（6）

式中：M为转子的质量；D为阻尼系数；K为刚度系数；x为转子的位移；F为外部激励力；x'为x的导数，表示速度；x\"为x的二阶导数，表示加速度。

公式（6）描述了转子受外部激励力和阻尼作用下的动态响应，确定了系统的动态行为。

控制目标为转子位移、速度或加速度的精确跟踪，从而提高了系统稳定性，控制目标计算方法如公式（7）所示。

（7）

式中：xd、xd'和xd\"分别表示期望的位移、速度和加速度。

为了实现这些控制目标，需要设定相应的性能指标，本文设计为误差的二次范数，如公式（8）所示。

（8）

式中：ex=x-xd；ex'=x'-x'd；ex\"=x\"-x\"d。

误差的二次范数可衡量系统跟踪期望轨迹的能力。通过优化误差的二次范数，可进行更精确的跟踪和控制。

在本文设计的轴承转动同步控制系统中，需要减少控制过程中产生的超调，使伺服系统能够稳定工作[5]。当系统输出值接近目标值时，需要控制回路开环，抑制反向超调，增加伺服系统的阻尼量，达到合理控制的目的。本文引入神经元来提升控制系统的自适应性，优化误差的二次范数e，运用PID控制器进行生成并获得控制信号，如公式（9）所示。

e（t）=ke（t）+Df [e（t+1）] （9）

式中：f [e（t+1）]为阻尼含糊。

通过运用阻尼系数来反映超调的抑制程度。当系统发生反向超调现象时，其特征关系应通过映射至单输出的模糊控制器来进行调整与优化。设定允许误差为3Q，输入变量论域，其集为I={x，y，z}。分析输出论域与输入论域的符号是否相异[6]。存在异常时，产生反向超调V。其中V越大，表示抑制程度就越大。当3Q超过设定阈值时，减少阻尼系数并提高控制信号的增益。采用模糊加权法进行去模糊化。设定m（n）为超调数量，对阻尼函数进行修正可以实现控制器的伺服控制[7]，其修正过程如公式（10）所示。

（10）

式中：β为修正系数。

当β＞1时，需要通过α×β来增加阻尼量，从而防止超调量继续增加；当β＜1时，需要加入补偿系数，使e（t）=0，释放多余能量。

运用控制器对系统的动态特性进行控制，确保轴承参数在设定范围内，以完成多模态控制。其中主轴转动调控系统的负载能够为设备进行关节轴承提供摩擦力矩，其所受负载的转矩如公式（11）所示。

R=Ffl （11）

式中：f为轴承相对运动状态；l为关节轴承时的主轴轴线距离；F为摩擦动力系数。

通过速度反馈可以增加系统的阻尼，从而能更准确地反映超调量[8]。在轴承铆接过程中，运用传感器检测主轴载荷，当输出载荷达到设定载荷R时，保持设定载荷的极限下压量并进行保压，完成轴承转动模糊整定伺服控制。

2 试验测试与分析

2.1 搭建试验环境

搭建火电厂热能动力设备轴承伺服控制的总体仿真模型，以确定伺服控制参数。在仿真条件下，采用的热能动力设备参数见表1。

在试验平台中，通过调试设备和传感器等分析轴承的转动状态，使用CIT程序来提取轴承特征频率。在数据采集过程中使用的采集卡的分辨率为25bit，最大电压采集范围为-4V～4V，激励电流为3A，动态范围为101dB。同时，在硬件参数方面，使用一个带有数据采集功能的振动传感器进行数据采集。该传感器具有高精度和高采样率，采样频率为10kHz，传感灵敏度为15.8mV/m·s2，最大传感加速度为100m·s2，谐振频率为7500Hz，激光转速测量范围为15000r/min。使用一个IIR低通滤波器，该滤波器的阶数为8，截止频率设置为500Hz。轴承转子转速范围为1000r/min～2000r/min。为了满足轴承同步伺服控制分析需求，将lab作为数据采集软件以实时采集变化的轴承数据。由于通道使用一个时钟会给结果带来偏差，因此需要使用DSQ来进行同步测量。安装激光转速器，设定合理的采样频率，并及时调整试验位置。

为了验证轴承转动同步控制方法的效果，本文设计了一个试验环境。神经网络学习率为0.01，遗忘因子为0.001，PID控制器比例系数为0.8，积分系数为0.5，微分系数为0.2，阻尼系数为0.7。整个试验环境设置完善且精确，确保试验数据的准确性和试验结果的可靠性。

2.2 结果与分析

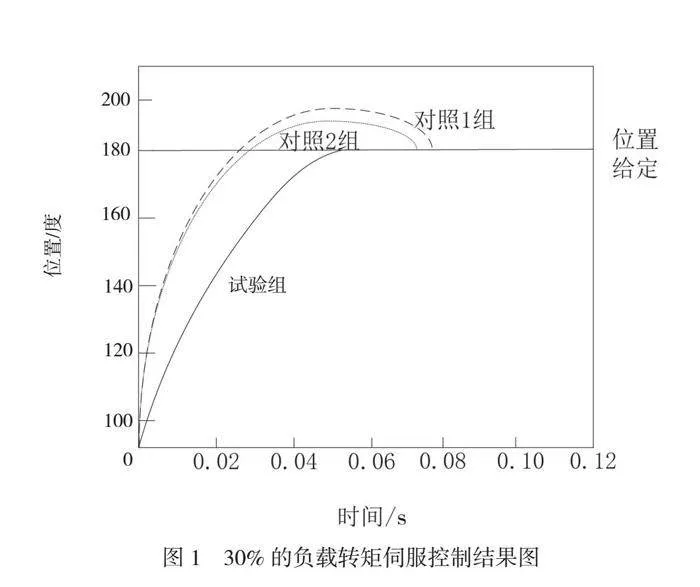
在仿真环境中，在负载转矩为30%的情况下设置3个小组。使用本文方法的小组为试验组，使用传统方法的2个小组为对照1～2组，对负反馈后的伺服控制效果进行分析，所得结果如图1所示。

由图1可知，2个对照组的轴承转矩位置控制存在超调，增加了系统对非连续位置给定的超调，响应速度变慢，无法合理调节伺服电机的转速和输出扭矩，存在稳态误差。而试验组在0.06s达到了给定位置，对轴承的旋转位置进行了精确控制，说明运用本文伺服控制方法能够在不同的负载转矩条件下合理调整位置的超调，当负载转矩较小时增大超调，反之则调小，从而减少稳态误差的产生，更精确地进行系统伺服控制。

为了验证本文控制方法的跟踪特性，需要对轴承的旋转速度进行测试。结合不同的工况，设置10组测试，所得结果见表2。

由表1结果可知，10组测试的轴承转速均在28r·min-1以内，结果符合预期。说明运用本文控制方法能够精准控制轴承的旋转位置和速度，实现高精度的设备运行。通过实时监测轴承的旋转状态并调整伺服电机的转速和输出扭矩，可有效减少设备运行过程中的振动和噪声，提高设备的稳定性，取得良好的控制效果。

综上所述，运用本文轴承同步伺服控制方法，可以根据不同的工况进行自适应调整，具有较强的适应性，原因是本文的轴承同步伺服控制方法综合运用了振动信号特征参数分析、神经元提升控制、PID控制和阻尼函数修正等方法，使控制方法具备较强的自适应性、控制精度和超调抑制能力，能够满足不同工况下的轴承转动控制需求，并提高系统的稳定性和可信度。该方法可广泛应用于各种设备，减少设备运行过程中的能量损失和浪费，达到节能环保的目的，并提高火电厂热能动力设备的运行效率，取得良好的控制效果。

3 结语

本文从火电厂热能动力设备入手，研究了轴承伺服控制等有关问题，探究了火电厂热能动力设备轴承同步伺服控制方法。通过确定轴承同步伺服控制的目标，并根据设备的工作原理和结构特点，建立轴承同步伺服控制数学模型。进而实时监测设备的运行状态，根据控制算法进行相应调整和控制。

参考文献

[1]段卓琳，蒋雨菲，杨金波，等.一种同步伺服控制系统电磁兼容总体优化设计方法[J].微特电机，2023，51（6）：40-44.

[2]黄依婷，沈建新，王云冲，等.基于递推最小二乘法观测器的永磁同步伺服电机变参数滑模控制[J].中国电机工程学报，2022，42（18）：6835-6846.

[3]谭华军.双三相永磁同步电机位置伺服系统前馈反馈复合控制[D].镇江：江苏大学，2021.

[4]王旭，蒋奇.基于改进遗传算法的故障电液伺服系统控制方法研究[J].机床与液压，2022，50（4）：167-172.

[5]李浩东，李长兵.永磁同步伺服系统摩擦力和扰动补偿方法研究[J].电机与控制应用，2022，49（1）：22-27.

[6]闵为.气动伺服系统自适应控制方法研究[J].液压与气动，2010（9）：11-13.

[7]郭子冉，杨明.应用于电机轴承和不对中复合故障的RNN诊断方法[J].南京航空航天大学学报，2022，54（增刊1）：87-93.

[8]魏东辉，汪霭廷，计京鸿，等.永磁直线同步电机自适应模糊分数阶滑模精密运动控制[J].吉林大学学报（工学版），2021，51（6）：2295-2303.