基于优化神经网络的二自由度机械臂轨迹跟踪

摘 要：针对二自由度机械臂的轨迹跟踪问题，本文提出基于改进微分进化优化神经网络的二自由度机械臂轨迹跟踪方法。分析其动力学方程，从周期性振动、瞬态响应和稳定运动状态3个角度探讨了二自由度机械臂的动态行为表现形式，将轨迹跟踪转化为求解二自由度机械臂非线性微分方程。采用约束处理机制改进基本微分进化算法，利用多层感知器（Multilayer Perceptron，MLP）结构的神经网络跟踪二自由度机械臂轨迹。测试结果表明，跟踪误差始终保持在0.010 m以内，最大值为0.010 m，最小值为0.003 m，与对照组相比具有明显优势。

关键词：改进微分进化；优化神经网络；二自由度机械臂；轨迹跟踪；动力学方程；动态行为表现形式；约束处理机制；MLP结构

中图分类号：G 254 " " " " " 文献标志码：A

二自由度机械臂是一种有2个旋转关节的机器人，运行特性独特，其运动学模型相对简单，由于关节旋转，其运动学方程是非线性的[1]，对机器人进行精确控制和轨迹跟踪的难度较高，因此，要完成特定的轨迹（即机器人末端执行器的路径和速度），须对二自由度机械臂进行精确的轨迹规划。为了进行精确的轨迹跟踪，需要高精度的控制器。在实际应用中，除了机械臂自身的因素外，还要考虑环境因素的影响，须结合优化算法、先进的控制策略和传感器技术，对二自由度机械臂进行精确控制和轨迹跟踪，还须不断调整和优化控制策略，以适应各种复杂的工作环境，满足不同的任务需求。李东民等 [2]提出以模糊滑模反步控制为基础的机械臂轨迹跟踪方法， 卢紫超等[3]提出以干扰观测器为基础的机械臂轨迹跟踪方法，它们都在一定程度上提高了跟踪精度，但是在二自由度机械臂方面存在局限性。

为此，本文提出基于改进微分进化优化神经网络的二自由度机械臂轨迹跟踪研究，在对比环境下分析本文设计的轨迹跟踪方法的性能。

1 二自由度机械臂轨迹跟踪方法设计

1.1 二自由度机械臂动力学模型构建

二自由度机械臂是1个试验装置，其构造简单、成本低，作为被控对象，它是一个不稳定、多变量、非线性并且强耦合的多输入、多输出系统。二自由度机械臂“不稳定”的特性说明在没有外部干预的情况下，机械臂无法维持其状态，而是会随时间产生变化。“多变量”和“非线性”特性说明机械臂运动受到多个因素综合影响，这些影响之间的关系并非简单线性关系。“强耦合”说明机械臂的各个部分之间联系联系紧密。1个关节运动可能会影响另一个关节运动，甚至可能显著影响整个机械臂的运动轨迹。这种耦合性要求控制系统能够全面考虑各个部分之间的相互作用，做出合理的控制决策。从动力学角度进行分析，二自由度机械臂主要由2个连杆组成，每个连杆对应一个转动关节[4]。由于关节旋转，因此机械臂在运动过程中会受到动力学效应影响，例如科里奥利力和离心力，这些力会干扰机械臂的运动，影响其精确控制和轨迹跟踪。由于每个关节都会受到其旋转范围的限制，因此这会影响机械臂的整体运动范围和轨迹跟踪。在实际操作中，须保证机械臂的关节角在允许的范围内。在此基础上，本文利用非线性微分方程分析二自由度机械臂的动态行为表现，主要为关节角度的变化。非线性微分方程是一个包括未知函数及其导数的方程，导数的值取决于函数自身的值。非线性微分方程可以说明二自由度机械臂关节角度的变化率与关节角度以及其他参数有统计学意义。求解这个非线性微分方程，可以得到关节角度随时间的变化关系。

结合实际需求，这些变化是周期性的振动，也是瞬态的响应，还是稳定的运动状态[5]。具体表现取决于初始条件、驱动力矩和阻尼等因素。结合上述分析，根据牛顿第二定律和转动惯量，二自由度机械臂的动力学方程如公式（1）所示。

τ=M（θ）d2θ/dt2+C（θ，dθ/dt）dθ/dt+ G（θ） （1）

式中：τ为关节驱动力矩；M（θ）为二自由度机械臂连杆的质量矩阵，其元素为各连杆的转动惯量；C（θ，dθ/dt）为科里奥利矩阵，其元素为各连杆的科里奥利力矩；dt为机械臂在t时间内进行动态运动的加速度向量；G（θ）为机械臂连杆θ的重力向量，其元素为各连杆所受的重力矩；t为时间。按照上述方式，利用二阶非线性微分方程，描述机械臂在关节驱动力矩作用下的动态行为。将驱动力矩作为输入，能够精确地描述机械臂在动态运动过程中的加速度和速度变化。求解这个二阶非线性微分方程，可以得到机械臂在给定驱动力矩作用下的运动轨迹。利用这个轨迹，进一步设计控制策略，精确跟踪机械臂的轨迹。控制策略的目标是调整驱动力矩，使机械臂的实际轨迹与期望轨迹尽可能接近。

结合上文构建的二自由度机械臂动力学模型，本文对二自由度机械臂的动态行为表现形式的划分结果见表1。

结合表1的分析结果，更准确地预测和控制机械臂的动态行为轨迹，在后续研究中，可以使用合适的方法来求解非线性微分方程，并考虑各种实际因素，例如摩擦力、弹性力和空气阻力。摩擦力会阻碍机械臂运动，产生阻力，使机械臂运动变缓，速度和加速度变慢。弹性力主要来自关节和连杆的弹性。当机械臂运动时，关节和连杆会发生弹性变形，从而产生弹性力。弹性力可能会改变机械臂的运动轨迹，使其偏离理想轨迹。空气阻力与机械臂的形状、速度和运动方向有统计学意义。当机械臂在空气中运动时，会受到空气阻力影响，空气阻力可能会使机械臂的运动轨迹发生偏离，当高速运动时，这种偏离会更明显。综合分析这些因素可能会对机械臂实际运动轨迹带来的影响，最大程度地保证跟踪结果的可靠性和精准性。

1.2 基于改进微分进化优化神经网络的二自由度机械臂轨迹跟踪

结合第1.1节对二自由度机械臂动力学模型的构建结果以及对二自由度机械臂的动态行为表现形式的分析结果，当对其轨迹进行跟踪时，本文在充分考虑摩擦力、弹性力和空气阻力因素作用强度的基础上，利用改进微分进化优化神经网络求解二自由度机械臂非线性微分方程。微分进化是一种全局优化算法，利用种群搜索的方式寻找最优解。为了提高搜索效率和精度，改进微分进化算法，增加了多样性的保持机制、自适应调整交叉和变异算子的参数等。

微分进化算法（Differential Evolution Algorithm，DE）是一种基于群体的随机优化算法，本文主要利用其解决实际参数优化问题。引入约束处理机制改进基本微分进化算法，保证搜索过程不偏离可行解区域，提高算法的实用性和可靠性，如公式（2）所示。

∆d=u（γ）q " " " " " " " （2）

式中：∆d为对神经网络中神经元参数的调整幅度；u（γ）为机械臂对应的矩阵关系；γ为关节空间中的各关节转动的角度；q为当前关节的状态向量。结合神经网络与微分进化算法，利用神经网络求解非线性微分方程。神经网络是一种强大的非线性映射工具，能够逼近任何非线性函数。采用多层感知器作为神经网络的结构，输入层包括关节角度和时间等信息，输出层为控制信号。训练神经网络能够找到最佳的权重和阈值，使神经网络的输出尽可能地接近期望轨迹。

这样的改进措施使改进的微分进化算法能够更好地处理复杂、非线性、高维度和大规模的二自由度机械臂非线性微分方程求解问题。

在此基础上，利用优化后的神经网络求解二自由度机械臂的非线性微分方程并确定其轨迹，具体操作步骤如下。

步骤一：明确求解的问题是一个二自由度机械臂的运动轨迹问题。目标是找到满足给定初始条件和边界条件的机械臂轨迹。

步骤二：收集历史数据，包括不同时刻的关节角度、关节速度、关节加速度和驱动力矩等。

步骤三：设计合适的神经网络结构。由于跟踪机械臂为二自由度结构形式，涉及2个连杆和2个关节角度的分析，因此，本文采用多层感知器（Multilayer Perceptron，MLP）结构。其中，输入层的节点数应与输入特征的数量相匹配。使用改进的微分进化算法对神经网络进行优化，不断调整神经网络的参数，逐渐逼近最优解，即最佳的控制信号序列。二自由度机械臂输入层包括关节角度（θ1、θ2）和时间t，因此，输入层节点数为3。

根据经验或试验来确定隐藏层的节点数。增加隐藏层节点数可以提高模型的复杂性和拟合能力，也可能导致过拟合。本文设置隐藏层主要为Sigmoid激活函数，如公式（3）所示。

（3）

式中：f（t）为激活函数；p、pi分别为目标二自由度机械臂状态特征与输入特征。

输出层的节点数应与问题的目标数量相匹配。在本文研究中，步骤一已经明确了目标是二自由度机械臂的运动轨迹，预测关节加速度或角度变化率，因此输出层节点数为1或2。

步骤四：使用收集的数据训练神经网络。本文使用梯度下降法，不断迭代更新网络的偏置，神经网络能够学习非线性微分方程的解，如公式（4）所示。

（4）

式中：G（t）为非线性微分方程的解；e为神经网路的偏置；τ（θ，t）为二自由度机械臂连杆θ在t时间内运动的动力学方程；[τ，τ（θ，t）]为二自由度机械臂连杆动力学方程的集合。步骤五：在神经网络训练完成并验证有效的前提下，使用其跟踪二自由度机械臂的轨迹。输入初始条件（例如初始关节角度和速度），神经网络将输出预测的关节角度变化，形成轨迹。

基于改进微分进化优化神经网络的二自由度机械臂轨迹跟踪方法具有许多优点。首先，它能够处理复杂的非线性问题，在机械臂的运动控制过程中，由于机械臂的动力学特性和外部环境的复杂性，经常需要面对各种非线性的挑战。改进微分进化优化神经网络的非线性映射能力十分强大，能够精确地模拟和预测这些非线性关系，从而显著提高轨迹跟踪的精度和稳定性。其次，它结合了神经网络的非线性映射能力和微分进化算法的全局搜索能力，形成了一种优势互补的组合。神经网络具有强大的学习和逼近能力，微分进化算法擅长在复杂的搜索空间中寻找全局最优解。结合这2种技术，该方法能够在轨迹跟踪过程中自动调整和优化控制参数，以适应不同的工作环境，满足不同的任务需求。最后，基于改进微分进化优化神经网络的二自由度机械臂轨迹跟踪方法具有强大的泛化能力，它可以应用于其他类型的机器人系统，无论是多自由度机械臂、移动机器人还是无人机等复杂系统，该方法都能够提供有效的解决方案，进行高精度的轨迹跟踪和控制，具有广泛的应用前景。

2 测试与分析

2.1 测试准备

本文以Kinova超轻型机器人系列中最新、最紧凑的成员——Gen3 lite作为测试对象。Gen3 lite机械臂各关节集成了的无刷直流电机，结构紧凑。每个关节都可以独立控制，用户能够选择工具和语言，适用于多种应用场景和环境。作为一款专业级机器人臂，其可以执行光操纵任务，能够在功能强大的Kinova＆Kortex开放式API软件上运行，与其他设备协作进行无缝共享编程。以此为基础，当对Gen3 lite二自由度机械臂轨迹进行跟踪测试时，分别设置文献[2]提出的以模糊滑模反步控制为基础的机械臂轨迹跟踪方法、文献[3]提出的以干扰观测器为基础的机械臂轨迹跟踪方法以及本文提出的基于改进微分进化优化神经网络的二自由度机械臂轨迹跟踪方法，在相同环境下进行对比测试。

2.2 测试结果与分析

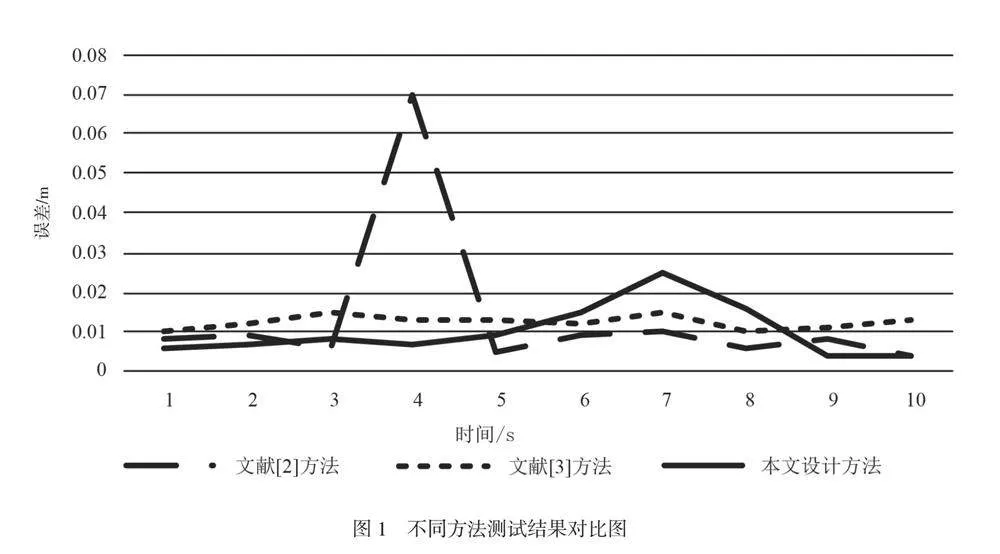
在上述测试环境中，分别采用3种方法对连续10 s内Gen3 lite二自由度机械臂轨迹进行跟踪，并统计具体跟踪误差，测试结果如图1所示。

从图1可以看出，3种不同轨迹的跟踪方法对应的误差情况出现了明显差异。使用文献[2]方法，整体跟踪误差波动较为明显，在测试过程中，时间误差基本控制在0.010 m以内，最大误差达到0.025 m，在接近停止移动阶段（测试时间的9 s～10 s），对应的跟踪误差稳定在0.005 m以内，说明该方法的收敛性存在进一步提升的空间。使用文献[3]方法，虽然整体跟踪误差相对稳定[6]，未出现较为突出的误差，但是对应的误差为0.010 m～0.015 m，说明该方法的跟踪精度存在进一步优化的空间[7]。使用本文方法，不仅未出现较为突出的误差，而且整体跟踪误差始终lt;0.010 m，最大值为0.010 m，最小值为0.003 m，与对照组相比优势明显。根据上述测试结果可以得出结论，本文提出的基于改进微分进化优化神经网络的二自由度机械臂轨迹跟踪方法可以进行精准跟踪，实际应用价值很高。

3 结语

随着工业4.0时代到来和智能制造技术的发展，工业制造领域对机械臂的轨迹跟踪精度和响应速度要求越来越高。为了满足这些需求，必须不断研究和改进轨迹跟踪技术。本文提出基于改进微分进化优化神经网络的二自由度机械臂轨迹跟踪方法，精准跟踪二自由度机械臂轨迹。在工业自动化生产线上，机械臂能够更精确地完成各种任务，提高效率。对一些高精度、高要求的制造任务来说，例如电子器件装配、药品生产等，机械臂能够提高轨迹跟踪精度，提升产品质量。轨迹跟踪技术涉及多个领域，包括机器人学、控制理论和计算机视觉等，本文研究能够推动机器人技术发展，促进相关学科交叉融合。

参考文献

[1]刘城焱，胡健，姚建勇，等.强化学习驱动下的柔性机械臂双时间尺度组合控制[J].控制理论与应用，2023，12（19）：1-11.

[2]李东民，王通，杜浩，等.基于模糊滑模反步控制的自动装卸钻杆机械臂轨迹跟踪研究[J].南京理工大学学报，2023，47（5）：619-628.

[3]卢紫超，李通，孙泽文，等.基于干扰观测器的机械臂广义模型预测轨迹跟踪控制[J].测控技术， 2023，42（9）：81-87.

[4]杨晓航，赵智远，李云涛，等.基于可操作度优化的冗余机械臂逆运动学求解方法[J].机械工程学报，2023，10（18）：1-12.

[5]王策，杨升，张磊，等.基于指数增益迭代学习的机械臂二阶滑模控制方法[J].化工自动化及仪表， 2023，50（5）：644-651.

[6]崔孟豪，姬会福，惠延波，等.基于RBF神经网络的七自由度凿岩台车钻臂运动学研究[J].机电工程，2022（9）：39.

[7]马宏达，邓义斌，郭强波.基于遗传算法的二自由度波浪能装置阵列优化[J].太阳能学报，2022（6）：43.