地铁列车收发车及检修计划优化方法研究

摘 要：本文意在解决地铁运营过程中的收发车和检修计划优化问题，提出了基于蚁群算法的地铁列车收发车与检修计划优化算法设计。采用0～1整数规划与决策变量的方式描述地铁列车的收发车与检修计划的关键决策因素，以车辆维护成本最低和利用效率均衡为优化目标、运营需求和检修需求为约束条件建立优化模型，利用蚁群算法对模型进行求解。现场应用测试表明本优化算法可以提高地铁列车的利用率并降低维护成本，具有一定的实际意义。

关键词：城市轨道交通；检修计划；蚁群算法；0～1整数规划模型

中图分类号：U 29" " " 文献标志码：A

地铁是城市轨道交通系统的重要组成部分。地铁运营单位根据运营时刻表与设备修程的要求，编制并实施收发车计划与检修计划，为市民提供高效、安全的运输服务。在计划实施过程中，收发车计划与检修计划间会相互影响，不同的收发车计划会使列车行驶里程发生变化，随列车行驶里程变化而触发的检修工作则会影响列车运用状态，进而影响执行收发车计划[1]。这种影响增加了计划编制的复杂程度。目前，人工编排计划已经不能满足现场使用，需要一种智能化手段实现收发车与检修计划的自动排程与优化，进而达到提升运营效率、降低运营成本的目的。为此本文提出一种基于蚁群算法的地铁列车收发车与检修计划优化算法设计。

1 收发车与检修计划优化算法设计

1.1 问题描述

地铁线路的运营时刻表规定了每天所有运营任务的出发/结束时间、区间运行时间、沿途各站的到站/出站时间等信息，是地铁进行运营工作的指令性文件。地铁列车的每日收发车计划可以看作是列车运用部门根据列车的当日状况，对当日运营时刻表中的运营任务分配适用车辆的集合。

地铁列车每日执行运营任务，行驶里程逐渐增加。当任意列车的行驶里程达到检修修程中规定的条件时，该列车就要进行检修工作。检修计划可以看作范围时间内所有列车检修工作的集合[2]。

实际运营中，车辆的行驶里程很难恰巧等于修程规定的检修间隔，因此对地铁运营企业来说，合理安排收发车计划，使列车尽可能在接近修程极限的情况下进行检修[3]，可有效避免过度检修，降低运营成本。

上述分析问题可以描述为给定列车运营规则、列车修程规则，输入列车数量、行驶里程和可用状态等参数的集合，输出指定时间范围内的地铁列车收发车与检修计划。问题的优化目标为减少列车的检修次数。约束条件包括每日运营任务必须全部执行、任意列车同一时刻只能执行一个运营任务、运营任务分为工作日和假日2类、列车按修程进行检修（不可欠修）以及同时检修的数量不能超过车辆基地的能力。

1.2 目标函数的建立

在实际运营中，检修任务的成本基本等于该任务的人工成本，检修过程中的零件消耗则按照故障维修计算，因此时间范围内的电动客车维护成本可表示为所有检修任务的总人工时，由此可得维护成本最低目标函数如公式（1）所示。

（1）

式中：M={m|m=1，2，3…Nm}为列车集合，m为列车序号，Nm为列车总数；D={d|d=1，2，3…Nd}为编制计划时间集合，d为日期的相对序号，Nd为计划总天数；S={s|s=0，1，2，3…}为检修修程的集合，s为检修项的编号；Bmds为0～1决策变量，表示当m号车在d日执行修程s时，Bmds=1，否则为0；Cs为s号检修作业的工时花费。

为避免运营任务分配过于集中，部分列车长期没有运营任务，停放过久，进而造成蓄电池亏损等问题，因此需要保证所有列车均有一定的出动比例，可看作所有列车既不执行运营任务，也不执行检修任务的状态的总时长最小，其目标函数如公式（2）所示。

（2）

式中：Q={q|q=0，1，2，3…Nq}为运营任务的集合，q为运营任务的序号，Nq为运营任务的总数量；Amdq为0～1决策变量，表示当m号车在d日执行q号任务时，Amdq=1，否则为0；Cd为一天内的运营时长。

将公式（1）、公式（2）2个优化目标函数进行整合并建立优化目标函数，如公式（3）所示。

minZ=α·Z1+β·Z2 （3）

式中：α、β分别为列车检修成本和均衡运用情况的权值，该数值为经验值，由列车历史数据分析产生。

1.3 约束条件的建立

每天的运营任务要区分平日与假日，并保证所有任务均被地铁列车执行，基于此建立运营时刻表使用约束，如公式（4）所示。

（4）

式中：δdq为0～1决策变量，运营任务q在d日被执行时，δdq=1，否则为0。

根据一个运营任务只能由一列电动客车承担的要求建立运营列车唯一性约束，如公式（5）所示。

（5）

根据任意列车同一时刻只能进行一项检修工作的要求建立检修工作唯一约束，如公式（6）所示。

（6）

实际运营中有早、晚高峰的需求，存在当天早高峰回库列车继续执行晚高峰任务的情况。假设列车m在d日执行运营任务q1的结束时间早于运营任务q2的开始时间，则列车m在q日执行q1、q2共2个运营任务，基于此建立运营任务调度约束，如公式（7）所示。

（7）

式中：Tqstar和Tqend分别为运营任务q的开始、结束时间。

由于存在早、晚高峰，因此存在同一天的早高峰回库列车继续进行检修的情况。假设列车m在d日执行运营任务q，q的结束时间早于检修任务s的开始时间，则列车m在d日执行运营任务q和检修任务s，基于此建立检修任务调度约束，如公式（8）所示。

（8）

式中：Tsstar'为检修任务s的开始时间。

根据车辆基地内每天同时进行的检修作业不能超过车辆基地最大检修能力的要求建立车辆基地能力约束，如公式（9）所示。

（9）

式中：Nc为车辆基地同时进行检修作业的最大数量。

列车执行多次运营任务后，其累计行驶里程逐渐接近修程规定的检修周期，当累计行驶里程无法满足可执行任意运营任务时，必须安排检修作业。计算列车当日行驶里程与前一次检修作业行驶里程的差值，将修程规定的检修周期与差值相减，所得结果如小于所有未来待执行的运营任务里程，可以安排该车辆进行检修。所建立的修程规则约束如公式（10）所示。

（lmd-lmds）+lqquest≤lsservice；m∈M，d∈D，q∈D，s∈S

（10）

式中：lsservice为第s号修程项规定的检修里程；lqquest为第q号运营任务的行驶里程；变量lmd为m号车在d日的行驶里程；变量lmds为m号车在d日进行s号检修作业时的行驶里程。

列车日常运营中常见“因故障扣车”等临时任务，可以将这些临时任务看作用时1d、检修周期无穷大的虚拟检修任务，长时间的临时任务可以拆解为多个用时1d的虚拟任务。所建立的临时任务约束如公式（11）所示。

Bmds=θmd；m∈M，d∈D，s∈S0 （11）

式中：θmd为0～1决策变量，当列车m在d日执行临时任务时，θmd=1，否则为0。

列车检修成本和均衡运用情况的权值α和β的约束条件如公式（12）所示。

α+β=1 （12）

1.4 基于蚁群算法的目标函数最优解求解

通过数学模型可以判断本节问题是一个以时间、顺序为二维特征且约束条件复杂的整数线性规划问题[4]，该类问题可以使用蚁群算法求解，其具体流程如图1所示。1）初始化迭代次数、蚁群数量、信息素浓度和信息素挥发率；初始化列车集合、日期集合、修程集合、任务集合和临时任务集合；初始化列车行驶里程和检修里程。2）迭代次数M=M+1。3）开始第K=K+1次（蚂蚁）搜索过程。4）筛选可用任务集合，顺序选取可用任务执行搜索计算，集合为空则跳转第11步。5）判断d日的列车m是否存在临时任务，跳转第11步，否则继续执行。6）筛选d日任务集合，如检索结果为空，跳转第9步，否则继续执行。7）判断检修约束，检索任务集合的所有元素，判断列车执行任务后是否超过检修周期，超出则该任务在d日任务集合中不可用。8）再次筛选d日可用的任务集合，如为空，判断列车执行检修任务，跳转第10步，否则根据选择规则选取列车。选取后该列车在当日可用列车集合中不可用。9）更新列车行驶里程，判断当日运营任务是否都已分配，未分配则跳转第4步，都分配则跳转第12步。10）获取当前检修承载能力，承载能力已满，则列车m闲置1d。11）根据修程合集、行驶里程、检修里程以及回库时间判断列车待执行检修修程s，更新检修里程，跳转第4步。12）判断d=D，如不等于则跳转第3步，如等于则表示本次（蚂蚁）的搜索计算完成。13）获取本代计算次数（蚂蚁）是否等于预设蚁群数量，不等于则跳转第2步。14）检索本代所有搜索结果（计算路径），带入各计算变量、常量，对模型目标函数进行求解，筛选本代最优解结果并更新信息素。15）判断迭代次数结束条件，未结束则跳转第1步。16）输出最优解，转制输出图形化的收发车与检修计划，算法结束。

2 算例分析和现场测试

为验证上述模型和算法的有效性，本文基于现场实例进行实证研究并收集现场数据，见表1～表3。

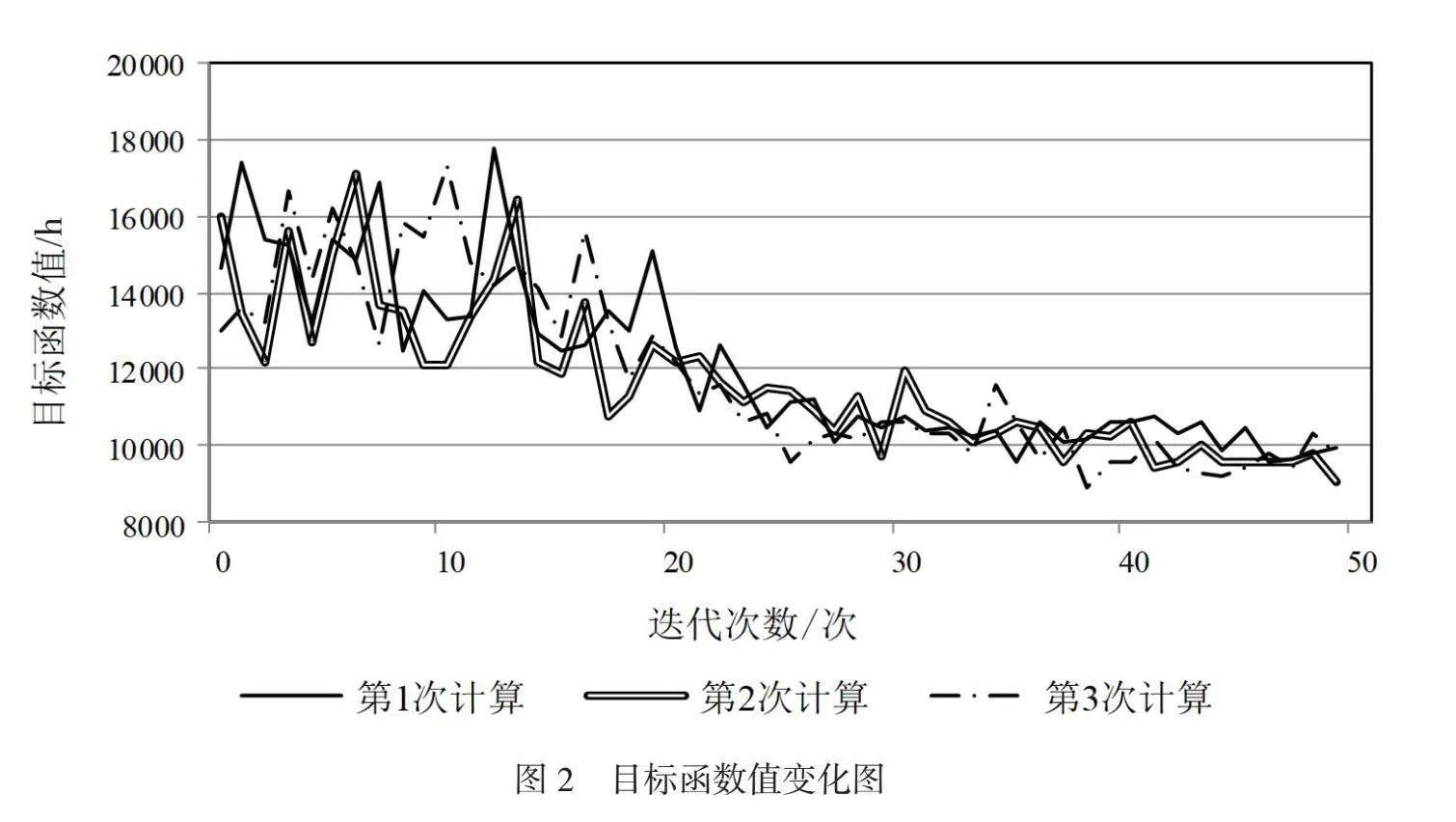
设置蚁群算法参数：蚁群迭代次数N=50，蚁群个体数量K=20，信息素浓度为1.0，信息素挥发速度为0.3。对算法执行3次，计算过程中的目标函数值变化情况如图2所示。

由图2可以看出，3次计算均发生优化目标值逐步下降，并随迭代次数增加而收敛的现象，表明蚁群算法对收发车和检修计划的求解优化有效。

算法生成的计划与历史同期检修数据比较见表4。由算法生成的计划可以满足运营任务的需求，检修任务S1、S2比历史同期减少8次和6次，以每次检修成本0.3万元和0.5万元计算，共计可节约检修成本5.2万元。

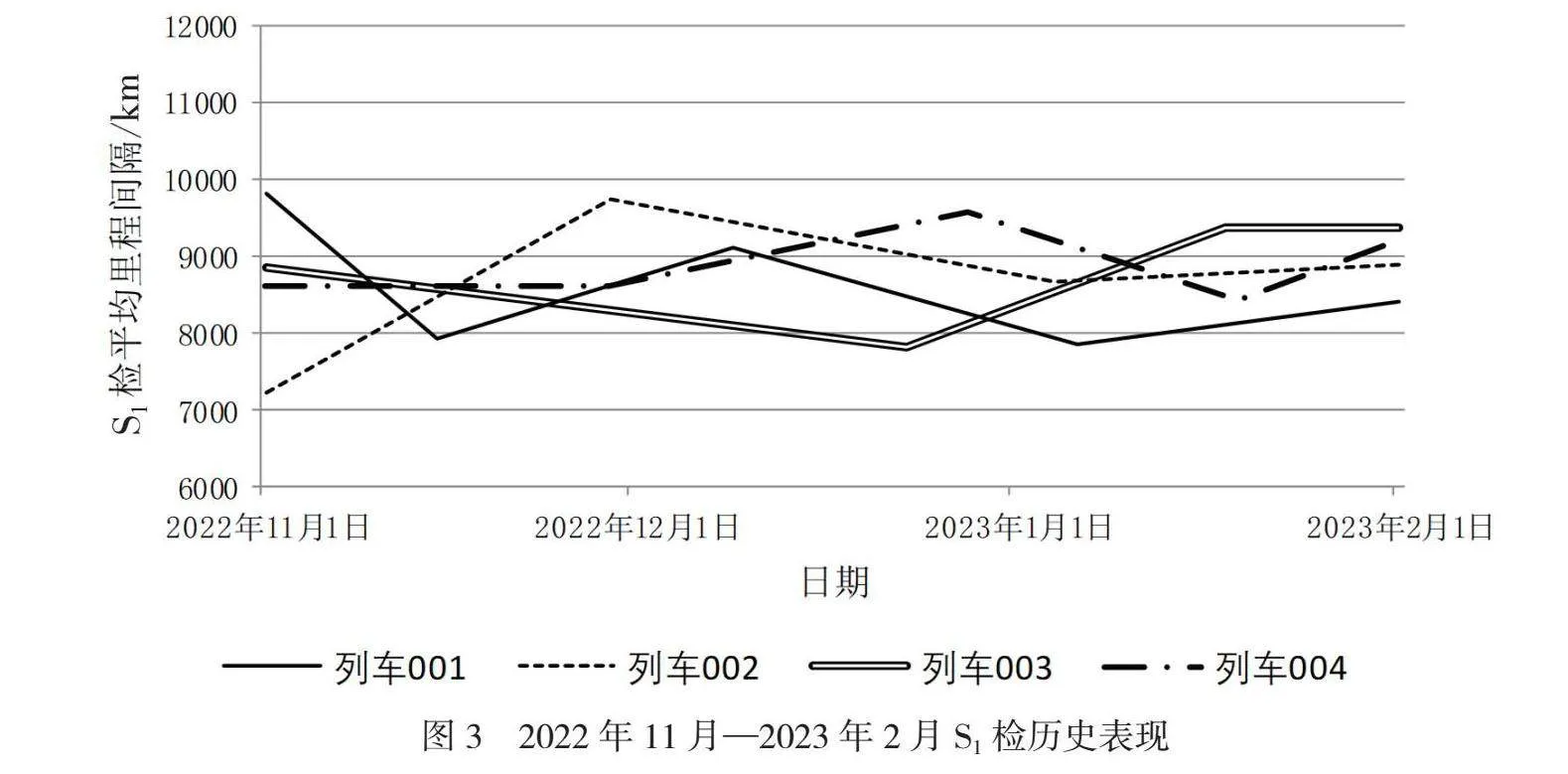
自2023年11月1日起使用算法生成收发车与检修计划进行现场测试。截至2024年2月1日，以S1检为例进行追踪，比较其测试期间表现和历史同期表现，如图3、图4所示。可以看出优化算法使用后，列车的检修间隔更稳定且表现比历史同期有所提高，S1检平均检修间隔由8827km提升至9583km。在运营总里程不变的前提下，提升平均检修间隔等同于减少检修次数，降低检修成本。

3 结论

本文基于地铁列车在日常运营中的实际使用情况，提出了收发车和检修计划优化问题，完成了数学模型搭建，设计了求解算法，并带入现场实际数据进行求解分析与现场测试。结果表明，本文提出的方法有效，是解决地铁列车运营计划排程与优化问题的可行方案之一，具有一定的实际意义与参考价值。

参考文献

[1]邓飞飞.浅述现代化城轨客车的维护与保养技术[J].科学与信息化，2017（21）：86-88.

[2]王家喜.动车所检修作业计划优化方法研究[D].北京：北京交通大学，2018.

[3]王忠凯，史天运，张惟皎，等.动车组运用计划和检修计划一体化编制模型及算法[J].中国铁道科学，2012（3）：102-108.

[4]杨舰.基于蚁群算法的分布式微电网控制方法研究[D].保定：华北电力大学（保定），2018.