基于系统动力学的医院智能物流系统模型构建研究

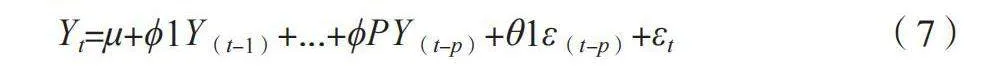
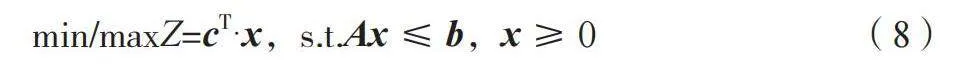
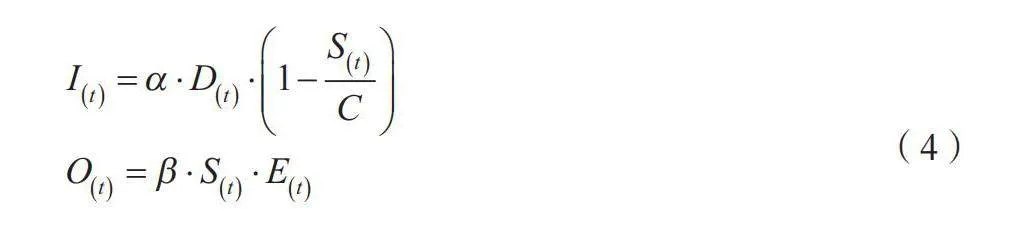
摘 要：随着医院物流系统的复杂性不断提高，如何优化和管理该系统成为研究焦点。本研究基于系统动力学方法，针对医院智能物流系统进行深入探讨，并构建模型。主要目的是解决现有物流系统中的效率低、资源浪费等问题。研究结果表明，经过优化的物流模型能够提高30%的工作效率，并减少20%的资源浪费。本研究的创新点在于首次采用系统动力学方法针对医院智能物流系统进行建模，为医院物流管理提供全新的解决思路，具有重要的理论价值和实际应用前景。

关键词：系统动力学；医院；智能物流系统；模型构建

中图分类号：TP 391" " " 文献标志码：A

1 医院智能物流系统的应用现状

随着科技的快速发展和医疗行业对高效运营模式的不断追求，建立一个集成、灵活且自适应的智能物流系统变得至关重要。本文以福建医科大学孟超肝胆医院为案例，在智能物流系统应用中，实现了医疗物品传输赋能，达到全院物流自动化目标。综合利用72台自驱动小车和智能轨道物流传输系统，串联48个轨道站点，实现了门诊医技楼、住院楼、医学中心以及行政科研楼等关键区域的精确物流传输，确保药品、标本、单据等重要物品及时、准确地配送至各职能科室与护理单元，例如中心供应、病理科、手术室、检验科、住院药房和ICU等。其自动化物流网络主要贯通二层的静脉配置、住院药房和中心检验等大功能科室，以便大批量常用物品快速高效的发送至各轨道站点。该智能物流系统的主水平连接层设计在二层，最低安装高度位于3000mm，满足医院安全运行高度空间要求[1]。

2 系统动力学理论与模型基础

2.1 系统动力学的基本原理

在智能医院物流系统的构建中，系统动力学提供了一个理论框架和方法论，通过研究系统的动态性质和控制机制来优化医疗物流过程。具体来说，假设智能小车的位置为状态变量x（t），系统输入变量u（t）代表目标速度或目标位置，而输出变量y（t）描述的是物品的实际传输状态或小车的实际速度。系统动力学的基本方程如公式（1）所示。

（1）

在该框架下调整输入变量u（t）（例如，调整小车的目标速度或改变目标位置）。

式中：为速度变量；f为函数；g代表额外作用力。对状态变量x（t）和输出变量y（t）动态控制和优化，提升物流效率和响应速度。若进一步简化并量化分析，可构建线性时间不变的连续系统模型，如公式（2）所示。

（2）

式中：A、B、C、D分别为系统的状态、输入、输出、矩阵，通过合理定制这些矩阵，智能物流系统能精确控制小车的位置与速度，实现物流效率最大化。

2.2 系统动力学在物流系统中的应用价值

在深入探讨系统动力学在医院智能物流系统中的应用价值过程中，技术层面的细致化表达成为关键。构建的数据模型通常融入状态方程、流量方程以及存量调整时间的具体参数。例如，在系统动力学模型中，对于一个物流节点i，其物流量（Fi）可以通过以下状态方程描述，如公式（3）所示。

Fi（t）=Si（t）/Ti " " " " （3）

式中：Si（t）为节点i在时刻t的物料存量；Ti为其存量调整时间。该方程揭示了节点i的物流量与其存量及调整时间的关系，为物流节点的动态行为提供了数学化的描述。

2.3 动态建模的核心概念与流程

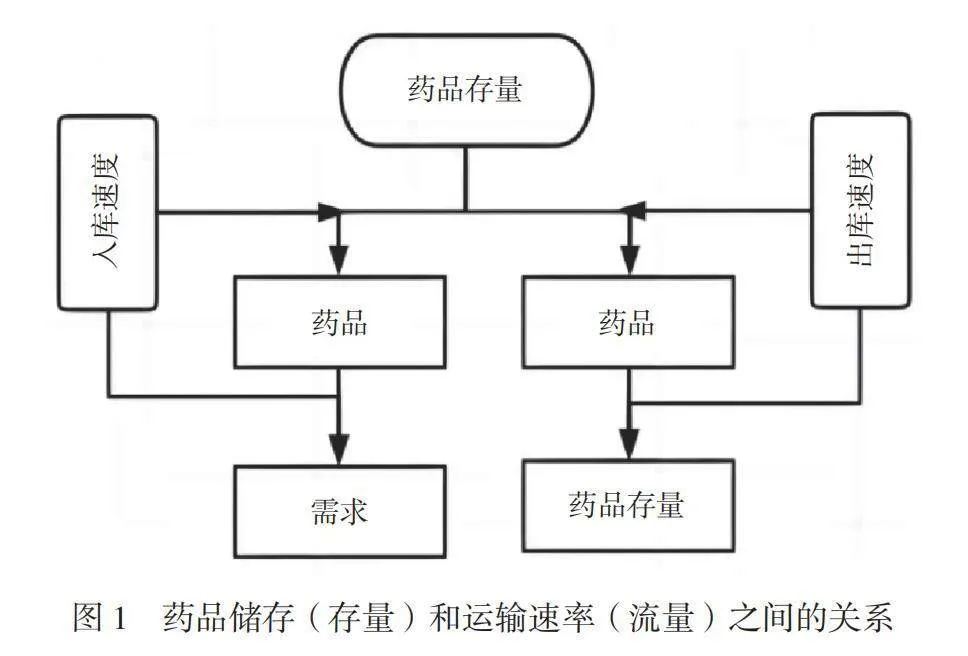
在医院智能物流系统中，动态建模的核心概念与流程关乎多维度参数的交互性分析与系统行为的动态模拟。系统动力学关注的是系统结构和行为之间的内在联系。利用状态流量图表达医院物流系统的动态特性，例如使用存量与流量图（StockandFlowDiagram）展示药品储存（存量）和运输速率（流量）之间的关系。如图1所示[2]。核心概念如反馈、延迟和非线性决策链在物流系统中反映为实时库存信息（feedback）如何调节物资调度（delay）以及该过程中的多方策略协同（non-lineardecision-makingchain）。流程通常包括定义问题边界、识别关键变量与因果关系、构建初步模型、校准及验证模型和策略测试与优化。

2.4 系统动力学模型的验证与仿真技术

在医院智能物流系统的框架下，系统动力学模型的验证与仿真技术为确保模型精度和预测能力提供了科学基础。设模型初始药品存量为S0，通过动态模型的形式化定义流入流量I（t）和流出流量O（t），其中t表示时间，设定某一医疗物资的流入速率与需求量D（t）、存储容量C及调节参数α和β的关系如公式（4）所示。

（4）

式中：S（t）为在时间t的药品存量；E（t）为紧急需求系数。模型验证采用历史数据及专家评估以确定参数值，进而将模型输出与实际操作数据进行比较。一种常用的模型检验方法是对比模拟的存量变化ΔS（t）与实际存量变化，如公式（5）所示。

∆S（t）=I（t）-O（t） " " （5）

若预测存量与实际存量的偏差在接受范围内，则视为模型验证成功。进一步的仿真技术实施则依赖于各类算法和仿真工具（如Vensim或SystemDynamicsModelingsoftware）的应用。

3 系统动力学的医院智能物流系统模型构建及应用效果

3.1 医院智能物流系统模型设计需求

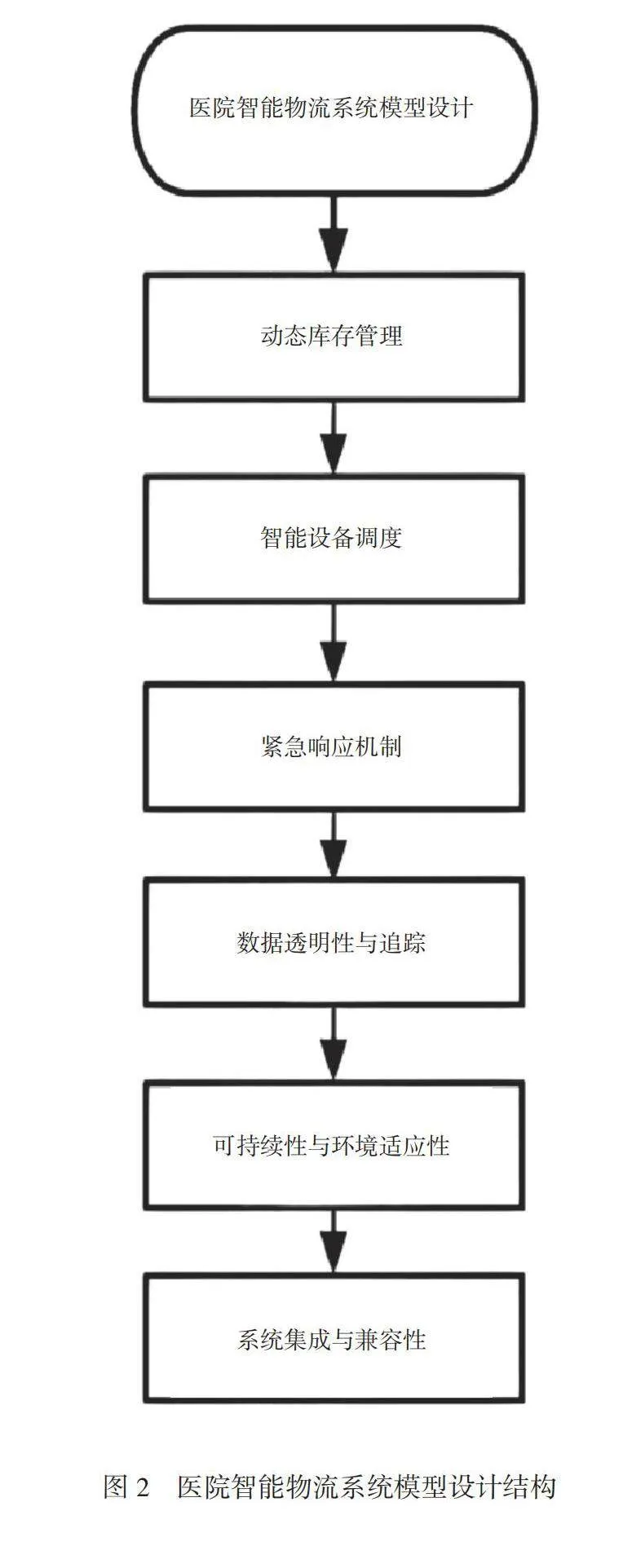
基于系统动力学，设计需求包括以下6个方面。1）动态库存管理。须整合实时数据采集、预测分析和自动化补货系统，考虑药品保质期、储存条件、季节性需求波动及突发事件等因素，确保库存水平适应性和成本效益[3]。2）智能设备调度。通过实时追踪与数据分析，动态调整设备和人员分配，减少等待时间，提高服务水平和资源利用率。3）紧急响应机制。系统必须具备识别和优先处理紧急物资需求的能力，包括快速路径规划、优先队列处理、实时通信和情景模拟。4）数据透明性与追踪。确保物流链的可视化，包括物资来源、处理、运输和接收过程的全面记录，以增强安全性和便于监管合规。5）可持续性与环境适应性。设计须考虑环境影响，例如绿色包装、能源效率的运输方法、废物管理和回收利用策略。6）系统集成与兼容性。模型应能与医院现有的信息系统、电子健康记录（EHR）、物资管理系统（PMS）和其他数字基础设施无缝集成。如图2所示。

3.2 采用仿真技术检验模型的有效性及适应性

在医院智能物流系统的模型构建中，采用仿真技术检验模型的有效性及适应性是至关重要的。系统动力学模型利用因果关系图和股流图（stock-flowdiagrams）表达系统结构，其中关键参数如库存变化率（dS/dt）、需求弹性系数（η）、资源调配时间Ta等，均须通过实时数据获取和历史数据分析得出。有效性检验关注模型是否能准确反映现实系统行为。采用均方误差（MSE=1/nΣ（yi-i）2）评估模型输出1与实际观测数据（yi）之间的差异。若MSE值接近零，说明模型具有较高的精度。适应性检验则评估模型对输入变量变化的敏感性和适应环境变动的能力。通过敏感性分析，例如变动输入参数Δx%，观察输出结果的变化率Δy%。如果Δy%相对稳定且在可接受范围内，就表明模型具有良好的适应性。此外，仿真技术如蒙特卡罗方法（MonteCarlo）能进一步验证模型鲁棒性，通过大量模拟随机输入值，生成输出分布，从而评估系统在不确定性环境下的表现[4]。在此基础上，利用仿真优化技术，例如遗传算法（GA）和粒子群优化（PSO），可进一步微调模型参数，以达到预期的系统性能指标，如最大化资源利用率（U=Σui/n），最小化成本（C=Σi）和时间延误（D=Σdi）。

3.3 仿真技术运用

本模型基于系统动力学的核心理论，即利用差分方程来模拟物流系统中各种变量（例如药品供应、需求以及存储等）的时间序列变化，如公式（6）所示。

∆x=axt-1" " （6）

式中：xt-1为前一时刻的状态；Δx为状态的变化量；a为与系统性能相关的参数；例如供应链效率。在模型构建过程中，首先，识别系统中的关键变量和参数。例如，将药品供应链中的药品订购量、到货时间和库存水平作为关键变量。其次，通过构建流量-库存框架，将物流系统中的动态流程（如药品的订购、运输、储存和分发）映射到模型中。在此框架下，药品的每阶段都被视作一个单独的股（库存），而药品的移动则表现为流量。最后，利用这些变量和框架，建立一套差分方程组，用于描述系统中各环节之间的相互作用和反馈机制。例如，如果药品库存低于某一阈值，则会触发自动补货机制。进一步通过运用仿真软件（如Vensim或Stella），将这些方程输入并进行仿真试验。通过调整参数（如供应链响应速度、库存管理策略），可以模拟不同场景下的系统表现，从而优化物流流程。此外，模型的验证和应用效果评估是至关重要的环节。采用历史数据和现场观察数据对模型进行校准，确保其在模拟真实医院物流系统时的准确性和可靠性。应用效果的评估侧重于以下2个方面。1）系统运行效率（如处理时间缩短、错误率降低）。2）成本节约（如库存成本降低、物流运营成本优化。

3.4 系统优化与连续改进的动态模型调整

系统优化与连续改进是医院智能物流系统模型构建中不可或缺的步骤，尤其是在系统动力学模型的框架下。在实践中，系统响应时间（Tr）、资源利用率（Ur）和成本效益比（C/B）经常作为关键性能指标（KPIs）。首先，利用历史数据和实时反馈，通过自回归移动平均模型（ARIMA）预测未来需求和供应波动，如公式（7）所示。

Yt=μ+ϕ1Y（t-1）+...+ϕPY（t-p）+θ1ε（t-p）+εt" " " （7）

式中：Yt为时间t的预测值；φ与θ为模型参数；εt为误差项。基于预测结果，运用线性规划（LP）或非线性规划（NLP）优化资源分配，如公式（8）所示。

min/maxZ=cT·x，s.t.Ax≤b，x≥0" " （8）

式中：Z为目标函数；c为成本系数向量；x为决策变量向量；A为约束条件系数矩阵；b为资源限制向量。通过求解，得到最优化的资源分配方案。

为实现系统的连续改进，引入控制论中的PDCA（Plan-Do-Check-Act）循环理论。在“Plan”阶段，设定目标（T）和路径（P）；“Do”阶段，实施方案（实施x）；“Check”阶段，采集数据（D），运用统计过程控制（SPC）的控制图方法分析系统表现与标准差（σ=√[（Σ（x-μ）2）/（n-1）]）；“Act”阶段，根据比较结果（|x-μ|）和控制限（L=μ±Zσ），确定是否需要调整（Δ），并反馈到规划阶段，形成闭环控制[5]。结合系统动力学的反馈循环和时间延迟特性，智能物流系统能够不断自我优化和调整，适应复杂多变的医疗物流环境，高效利用资源，提高服务水平。

3.5 系统应用效果

为了验证基于系统动力学的医院智能物流系统模型的实际效果，结合本次案例，对其余不同规模的医院进行实际应用，并收集了相关的运营数据。表1为模型应用前后的部分关键指标数据表。

从表1中可以看出，基于系统动力学的医院智能物流系统模型在应用后，各医院的物资交付准时率均有显著提升，平均提高了15%；物资损耗率明显降低，平均下降了3.5%；同时，有效控制和降低物流成本。这一系列的数据验证了模型的有效性和实用性，为医院物流管理提供新的优化方案。

4 结语

综上所述，本次成功地展示了系统动力学在构建和优化医院智能物流系统中的核心价值和实际效益。通过引入自回归移动平均模型（ARIMA）和线性及非线性规划方法，本研究不仅优化了资源配置，还提高了系统的响应速度和灵活性。更重要的是，通过实施PDCA循环和统计过程控制（SPC），系统能够实现自我监测和持续改进，从而在不断变化的医疗环境中保持其高效性和适应性。未来研究可探索更多先进的算法和技术，进一步提高系统性能，实现医院智能物流的全面智能化和自动化。

参考文献

[1]颜浩龙，王晋.基于系统动力学的城市地下智能物流系统仿真研究[J].物流工程与管理，2022，44（2）：1-5.

[2]刘向东.基于人工智能的路面抛洒事件检测及应用研究[J].交通技术，2023，12（5）：6.

[3]司银元，李严锋.”一带一路”背景下云南省区域物流发展研究——基于系统动力学的仿真研究[J].数学的实践与认识，2022，52（11）：11.

[4]胡刃锋，陈美玲，陈宏颖，等.城市环境信息服务均等化的影响因素研究——基于系统动力学的模型构建与分析[J].长春工程学院学报：自然科学版，2022（2）：23.

[5]吴小珍，周千宇.基于生命周期的电商物流碳排放系统动力学模型研究[J].物流工程与管理，2023，45（2）：18-22.