盾构施工土体参数全局灵敏度分析

摘 要：为准确研究地铁盾构施工引发地面沉降土体参数灵敏度，考虑地下水影响，以比奥固结理论为基础，考虑土体参数随有效应力的动态变化关系，建立地铁盾构施工引发地面沉降三维流固全耦合模型，以某地铁盾构隧道区间段为例，通过对比实测地面沉降量和计算沉降量验证模型的可靠性，在本次数值模拟计算的参数灵敏度分析中，采用生态模型中全局灵敏度分析法的Morris法。结果表明：地铁盾构施工引发的土体变形对变形模量、内摩擦角和重度最敏感，变形模量、内摩擦角和重度3个参数的灵敏度线性效应明显。

关键词：地面沉降；全局灵敏度分析；Morris法；盾构施工；比奥固结

中图分类号：U 455" " " " 文献标志码：A

要准确获取地铁盾构施工引发的地面沉降相关土体参数灵敏度，地面沉降计算模型及参数灵敏度计算方法的选取极为重要。

在地铁盾构施工引发地面沉降研究方面，以往的研究通常不考虑地下水影响，以简化模拟，同时考虑土体相关参数在整个模拟过程中均为定值。在实际研究的过程中，可以发现，地下水位变化对盾构施工引发地面沉降有很大影响[1]。

在参数灵敏度计算方面，由于局部灵敏度法并未考虑多参数变化下模型计算结果的变化，因此精度相对较低。全局灵敏度分析是在不同参数同时变化的基础上计算得出，采用这种方法计算得到的参数灵敏度更贴近实际情况，更客观[2]。

本文以比奥固结理论为基础，考虑土体相关参数随有效应力的动态变化关系，以西南某地铁盾构隧道区间为例，建立地铁盾构施工引发地面沉降三维流固全耦合模型[3]。采用全局灵敏度分析法中的Morris法对盾构隧道开挖层土体参数灵敏度进行了研究。

1 研究区概况

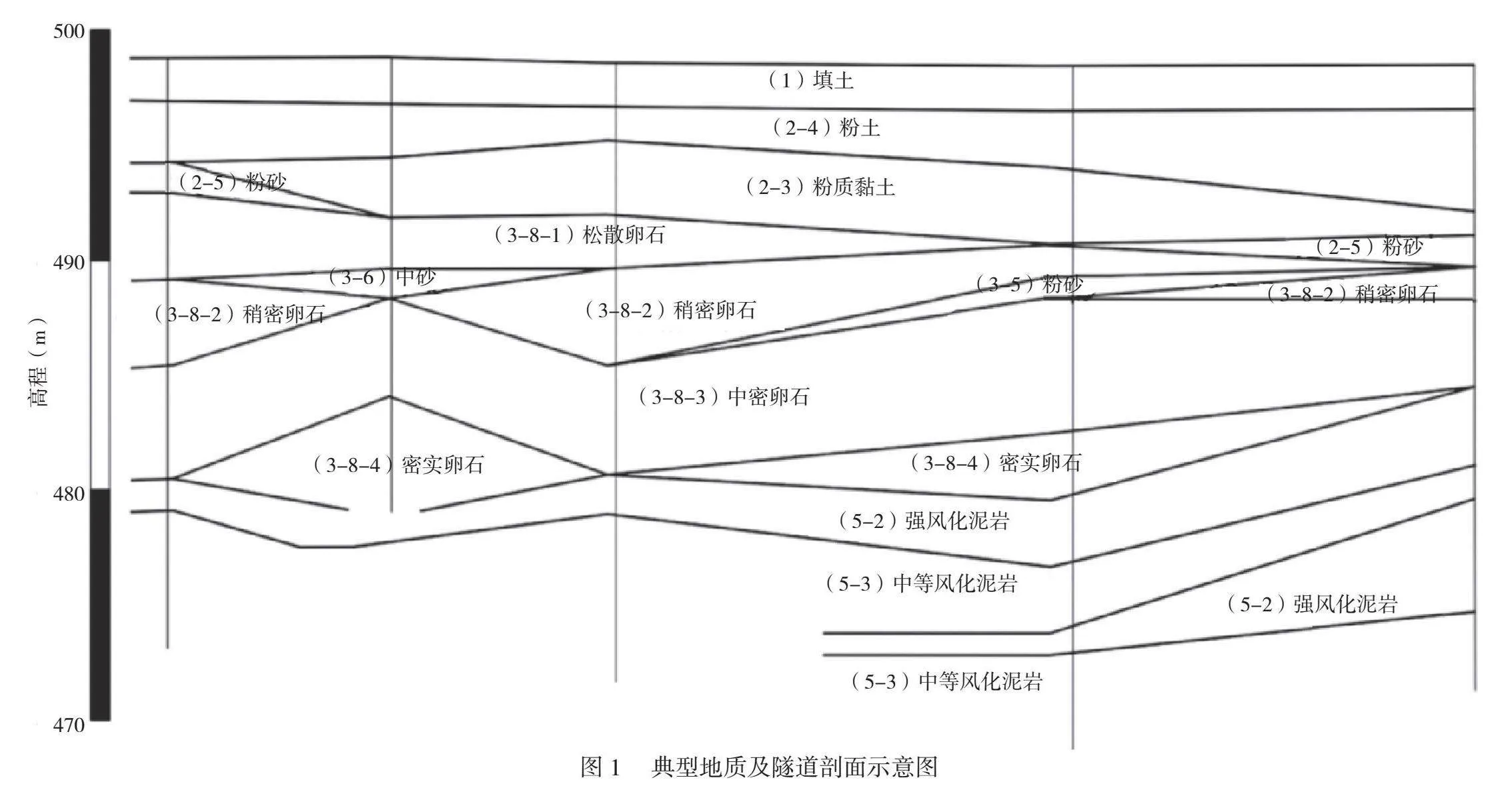
该盾构隧道位于西南地区，全线纵向长度约1384.50m。地面高程497.74～499.86m，盾构隧道区间顶埋深11～17m，底埋深16.5～23m。选取该区间段234m盾构隧道作为研究对象，典型地层剖面如图1所示。

2 概念模型

本次研究模型长度234m，宽（即y方向长度）80m，模型底板取-41m。模型共6层，盾构隧道施工位于4层。详勘报告中地下水位埋深8.1～8.5m，本次研究取初始地下水位埋深8.3m。初始应力取土体自重应力。模型四周边界考虑盾构推进速度较快概化为定水头边界，将模型底作为隔水边界。模型四周设置为水平约束，模型底部设置为固定约束，地表设置为自由边界。模型三维剖分图如图2所示。盾构施工过程中一些单元模拟，包括管片单元、浆体单元、盾构单元、盾尾空隙单元、土体单元、开挖面卸荷单元等，对本次研究的准确性非常重要，盾构施工模拟过程中涉及的单元如图3所示。在本次研究中，将盾构施工开挖单元视为“空气单元”，模量取极小值。对折减后的开挖面卸荷单元变形模量进行计算，以此来表示盾构隧道开挖导致开挖层土体卸荷情况。

衬砌管片结构采用C50钢筋混凝土，弹性模量为36GPa，折减系数为0.8，因此取28.6GPa，泊松比取0.17，密度为2300kg/m³，本次研究认为衬砌管片不透水，具体参数见表1。

3 数学模型

3.1 比奥固结理论

比奥在1941年首次提出比奥固结理论，假定土体为饱和土体，其土骨架变形为线弹性、微小变形，土体中发地下水渗流符合达西定律，且认为地下水不可压缩，为真三维固结理论，三维比奥固结方程如公式（1）所示[4]。

（1）

式中：Δ2为拉普拉斯算子，；G为剪切模量；wx、wy、wz为3个方向上的位移分量；v 为泊松比；u为孔隙水压力；kx、ky、kz为3个方向上的渗透系数；W为源汇项； γ为土的重度；γw为水的重度。

3.2 比奥固结有限元方程

采用伽辽金加权余量法离散方程，考虑到土体的非线性特性，取∆t时间内的位移增量来代替位移，将公式（1）离散成增量形式，如公式（2）所示[5]。

（2）

式中：∆δ为结点位移增量；为固体刚度矩阵；K为渗透流量矩阵；K'为应力—渗流耦合项矩阵；∆Q为流量增量矩阵；B为自由面的积分矩阵；R为等效节点荷载；Rt为t时刻已经发生的位移所平衡了的那部分荷载。

3.3 参数的动态变化模型

3.3.1 孔隙度与渗透系数的非线性

根据Kozeny-Carman公式和土力学中孔隙度的定义推导可得孔隙度n和渗透系数k的动态表达式[6]如公式（3）、公式（4）所示。

（3）

（4）

式中：n0为初始孔隙度；k0为初始渗透系数；εv为体应变，。

3.3.2 土体参数的非线性

采用邓肯—张非线性模型，将土体的本构关系推广到非线性，本构关系{Δσ}=[D]{Δε}中矩阵[D]的弹性常数E、v不再视为常量，而是随着应力状态改变而改变[7]，其切线弹性模量和切线泊松比的计算过程如公式（5）、公式（6）所示。

（5）

（6）

式中：Rf为破坏比；c为黏滞力；ϕ为内摩擦角；σ1为第一主应力；σ3为第三主应力；n为弹性模量与固结压力曲线的斜率；α、G为土体常规三轴压缩试验结果所绘曲线截距；F为土体试验参数；pa为大气压强。

3.4 Morris全局灵敏度分析原理

本次研究采用生态模型中经常使用的Morris全局灵敏度分析法进行分析，假定k个参数中每个参数取样点有p个，每个参数分别在对应的p个取样点上取值，可获得向量X={X1，X2，...，Xk}，构造m×k（m=k+1）阶矩阵B，如公式（7）所示。

（7）

式中：矩阵中每列为1个参数，数字1为参数取值已改变，数字0为参数为原值，即第一行为模型参数初始向量。假定相邻两行分别为第i-1行和i行，可以看出这两行只有一个参数的取值不同，令其变化为∆x，可计算出相应的模型输出结果yi-1和yi，参照局部灵敏度计算法，定义参数相对灵敏度Si'来表征位移对参数的敏感性，如公式（8）所示。

（8）

若随机生成r组初始参数向量，则可计算出k个参数r个相对灵敏度，参数i的相对灵敏度的均值di与标准差，σi如公式（9）、公式（10）所示。

（9）

（10）

参数均值大小与参数灵敏度大小相关，均值越大，参数灵敏度越高，而标准差则表示参数非线性作用大小或与其他参数间相互作用程度。标准差越大，则该参数非线性效应越明显，或者说该参数与其他参数相互作用程度越强，反之亦然[8]。

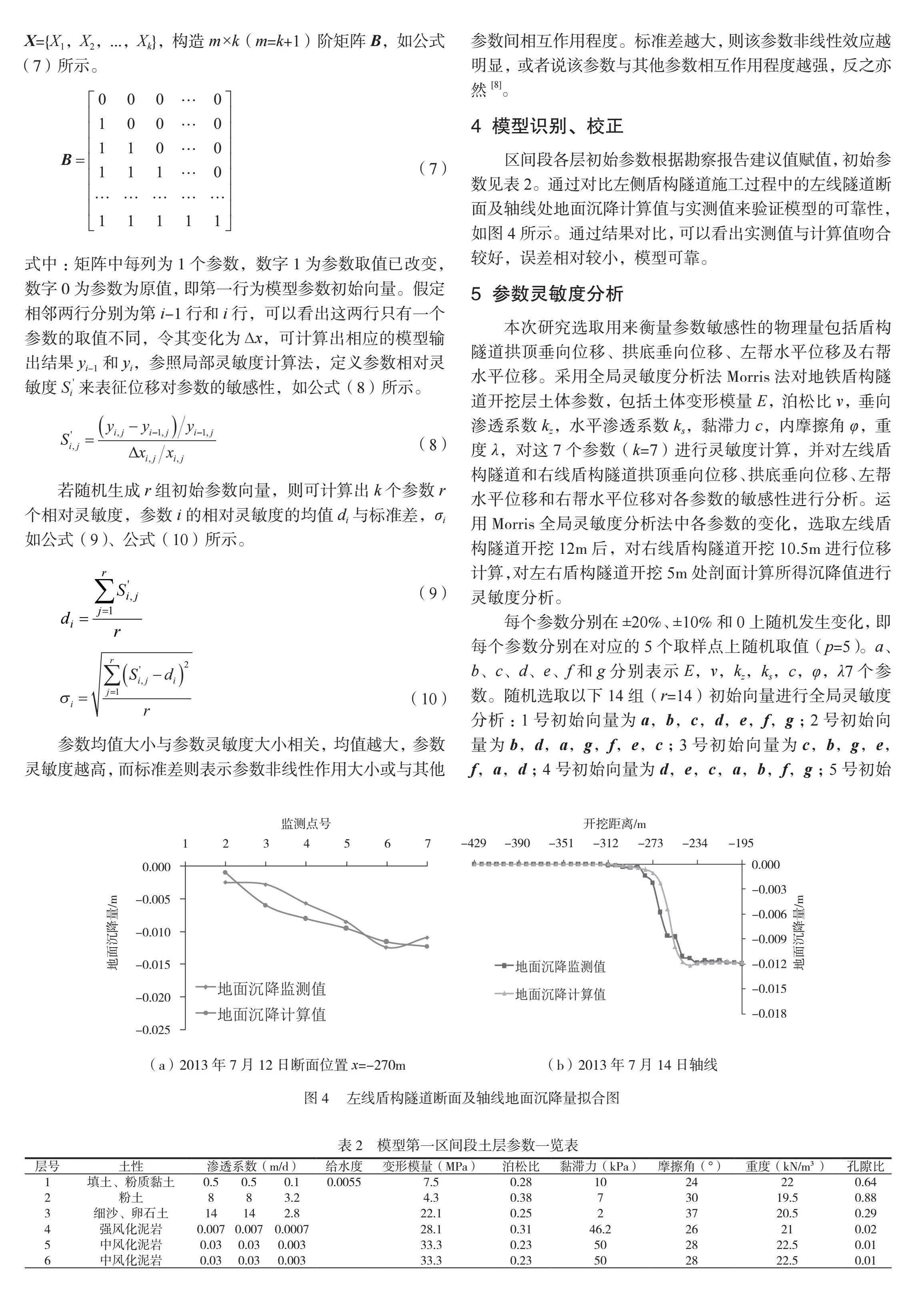
4 模型识别、校正

区间段各层初始参数根据勘察报告建议值赋值，初始参数见表2。通过对比左侧盾构隧道施工过程中的左线隧道断面及轴线处地面沉降计算值与实测值来验证模型的可靠性，如图4所示。通过结果对比，可以看出实测值与计算值吻合较好，误差相对较小，模型可靠。

5 参数灵敏度分析

本次研究选取用来衡量参数敏感性的物理量包括盾构隧道拱顶垂向位移、拱底垂向位移、左帮水平位移及右帮水平位移。采用全局灵敏度分析法Morris法对地铁盾构隧道开挖层土体参数，包括土体变形模量E，泊松比v，垂向渗透系数kz，水平渗透系数ks，黏滞力c，内摩擦角φ，重度λ，对这7个参数（k=7）进行灵敏度计算，并对左线盾构隧道和右线盾构隧道拱顶垂向位移、拱底垂向位移、左帮水平位移和右帮水平位移对各参数的敏感性进行分析。运用Morris全局灵敏度分析法中各参数的变化，选取左线盾构隧道开挖12m后，对右线盾构隧道开挖10.5m进行位移计算，对左右盾构隧道开挖5m处剖面计算所得沉降值进行灵敏度分析。

每个参数分别在±20%、±10%和0上随机发生变化，即每个参数分别在对应的5个取样点上随机取值（p=5）。a、b、c、d、e、f和g分别表示E，v，kz，ks，c，φ，λ7个参数。随机选取以下14组（r=14）初始向量进行全局灵敏度分析：1号初始向量为a，b，c，d，e，f，g；2号初始向量为b，d，a，g，f，e，c；3号初始向量为c，b，g，e，f，a，d；4号初始向量为d，e，c，a，b，f，g；5号初始向量为e，a，c，d，f，g，b；6号初始向量为f，a，d，c，e，b，g；7号初始向量为g，d，c，e，a，f，b；8号初始向量为a，d，e，c，g，b，f；9号初始向量为b，g，c，f，a，e，d；10号初始向量为c，g，e，f，d，a，b；11号初始向量为d，a，e，g，b，c，f；12号初始向量为e，c，f，a，b，g，d；13号初始向量为f，d，a，c，b，e，g；14号初始向量为g，c，f，a，d，b，e。计算所得灵敏度均取其绝对值。

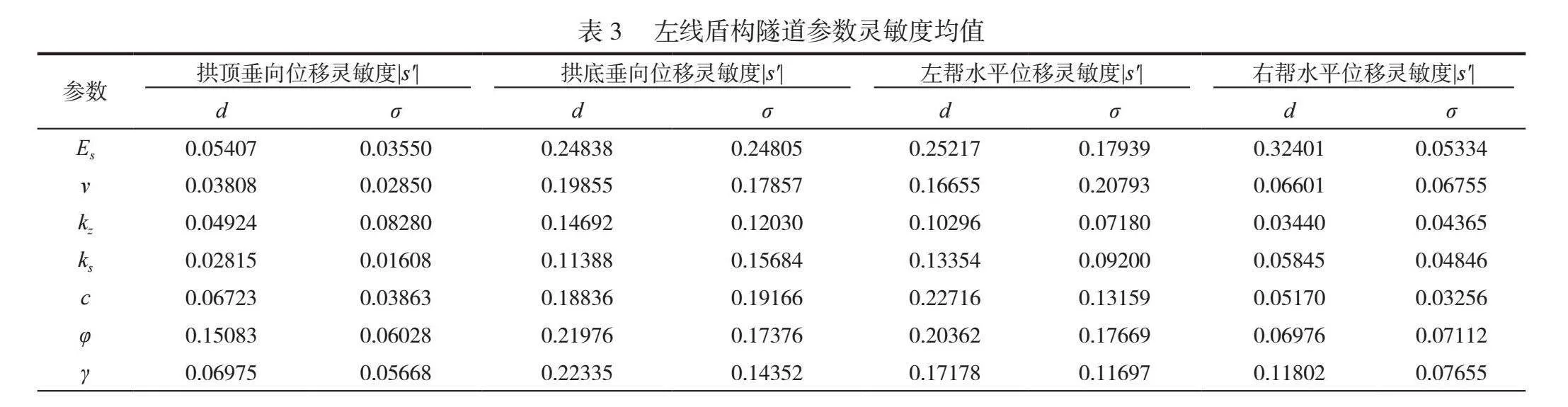
采用Morris法计算得到的各参数灵敏度均值见表3，由计算结果可知，对垂向位移及水平位移影响均较大的参数主要为变形模量、内摩擦角和重度，可以看出，土体变形对变形模量、内摩擦角和重度最敏感。

采用Morris法计算得到的各参数结果分析见表4。通过计算，由计算结果可知，对垂向位移来说，变形模量、内摩擦角和重度的灵敏度标准差较大；对水平位移来说，变形模量、内摩擦角、重度和泊松比的灵敏度标准差较大。而灵敏度标准差表示该参数的非线性作用大小或与其他参数之间相互作用的程度，与其他参数之间的作用程度主要是指在其他参数随机变化基础上，该参数若发生变化则会对模型计算结果有影响。如果标准差越小，就表示该参数非线性效应不明显或者与其他参数相互作用的程度越弱，即在其他参数随机变化的基础上，该参数若发生变化则对模型计算结果影响较小，反之亦然。由计算结果可以看出，对垂向位移来说，变形模量、内摩擦角、重度这3个参数的线性效应较为明显，与其他参数作用程度相对较强。对水平位移来说，变形模量、内摩擦角、重度和泊松比这4个参数的线性效应较为明显，与其他参数作用程度相对较强。综合考虑对垂向位移及水平位移的影响，变形模量、内摩擦角、重度的线性效应明显，与其他参数作用程度较强。

6 结论

通过研究，得出以下结论。1）本次研究所建立的考虑地下水影响的地铁盾构施工引发地面沉降三维流固全耦合模型，引入了土体水力学参数和土力学参数随有效应力的动态变化，更切合实际地刻画了土体中的应力应变关系，即随着土体应力应变的变化，提高了模型的可靠性，具有较强的理论意义和实用价值。2）通过使用全局灵敏度分析法中的Morris法对盾构隧道开挖层土体参数进行参数敏感性分析，得到开挖层参数中变形模量、内摩擦角和重度灵敏度最大，综合考虑对垂向位移及水平向位移的影响程度，变形模量、内摩擦角和重度灵敏度线性效应较为明显，与其他参数相互作用程度较强，即在其他参数随机变化的基础上，该参数若发生变化则会对模型计算结果带来较大影响。

参考文献

[1]贺少辉，张淑朝，李承辉，等.砂卵石地层高水压条件下盾构掘进喷涌控制研究[J].岩土工程学报，2017，39 （9）：1583-1590.

[2]徐成华，谈金忠，骆祖江，等.地铁盾构施工引发地面沉降三维流固全耦合数值模拟预测[J].南京大学学报（自然科学），2019，55（3）：409-419.

[3]骆祖江，李会中，付延玲.第四纪松散沉积层地下水渗流与地面沉降控制数值模拟[M].北京：科学出版社，2009.

[4]金玮泽，骆祖江，陈兴贤，等.地下水渗流与地面沉降耦合模拟[J].地球科学（中国地质大学学报），2014，39（5）：611-619.

[5]冉启全，李士伦.流固耦合油藏数值模拟中物性参数动态模型研究[J].石油勘探与开发，1997（3）：61-65，100.

[6]田杰，刘先贵，尚根华.基于流固耦合理论的套损力学机理分析[J].水动力学研究与进展（A辑），2005（2）：221-225.

[7]罗刚，张建民.邓肯-张模型和沈珠江双屈服面模型的改进[J].岩土力学，2004（6）：887-890.

[8]陈卓，骆祖江.比奥固结全耦合模型参数灵敏度分析[J].南昌大学学报（工科版），2017，39（4）：354-360，379.