城轨列车车底运用优化研究

摘 要：针对城市轨道交通车辆运用不均衡的问题，本文以单条城市轨道交通线路的车底接续方案为决策变量，已知车次计划及相关设备设施参数，在考虑车次接续次数要求、前后节点接续车底相同、不允许车底空驶运行、节点接续时空约束以及回段整备时间约束的基础上，构建车底运用计划优化模型，使车底数量、接续时间、车底均衡性差距的综合目标最小。利用蚁群算法对某条地铁线路进行求解，结果表明应用模型能得到多目标最小的车底运用计划。

关键词：不均衡；车底；优化模型

中图分类号：U 29" " 文献标志码：A

根据中国城市轨道交通协会统计，截至2023年9月30日，中国内地共有58个城市开通不同制式城轨运营线路308条，运营总里程为10841.59km，总体规模和建设速度都居世界第一。2022年全国城轨交通累计配属车辆为10425列，比去年增加767列，增长7.94%。但在实际运营过程中，配属车辆过剩、车辆运用不均衡问题比较突出，给各运营公司带来巨大的资金压力、“检修延时”或“检修提前”等问题。车底运用计划决定了车辆数量和使用效率，对城市轨道交通的正常运营具有重要作用，其编制质量对城轨运营的经济效益和服务质量有重大影响。

较多学者研究列车开行计划或时刻表，较少学者研究车底运用计划[1-2]。国内学者多在动车组运用研究的基础上将车底运用问题转换为TSP问题、商品流问题或路径选择问题，将车次任务接续转化为时空接续网络图[3]。而国外学者对车辆调度问题研究较多，通常将车辆调度问题转化为多商品网络流问题，并设计了多种算法进行求解[4-5]。

1 车底运用问题描述

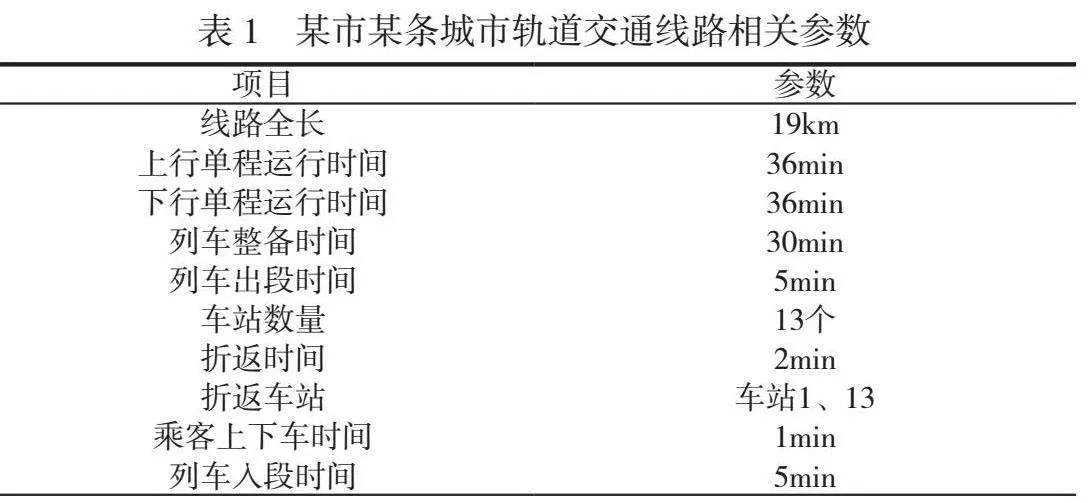
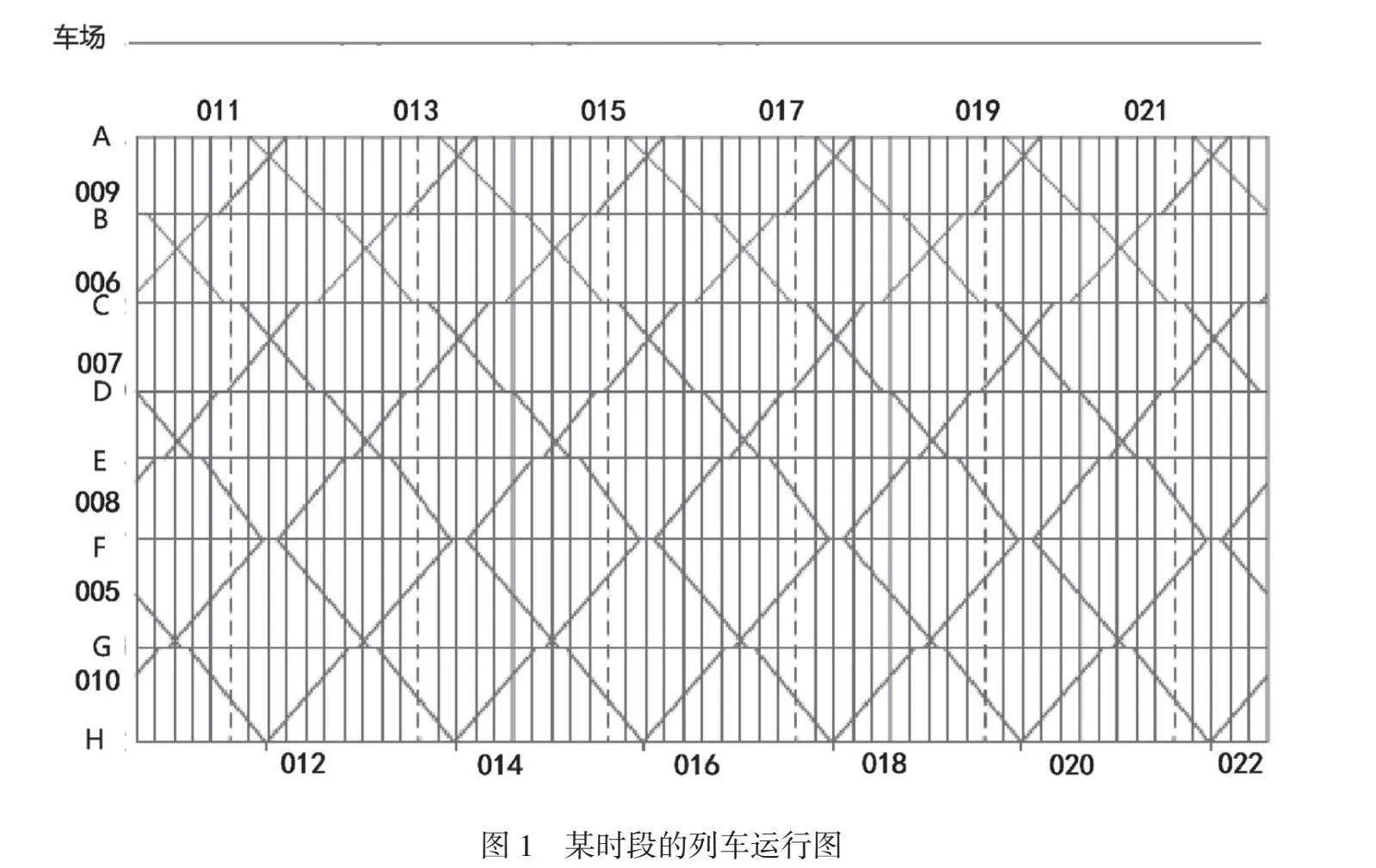
图1为某地铁某一时段的列车运行图，在列车运行图中详细地描述了列车运行轨迹、规定了各次列车占用区间的顺序以及列车在各车站的出发、到达时刻。该运行图共8个车站，1个车场，车站A和车站H是终点站，其中A站连接车场，上行有006、008、010、012、014、016、018、020、022次共9个运行任务，从车站H开往车站A；下行有005、007、009、011、013、015、017、019、021次共9个运行任务，从车站A开往车站H。当同一个列车车底连续承担两个运行任务时，需要满足的条件是后一个运行任务的始发车站和前一个任务的终到车站是同一个车站；后一个运行任务的始发时间应该比前一个运行任务的终到时间长，并且预留足够的接续时间供列车清客、折返以及跨线等作业。例如上行运行任务018的开始时间与下行运行任务009的结束时间之差满足折返时间的要求，那么该车底可以完成运行任务009后接续任务018，否则，需要考虑接续其他运行任务或者返回车场。如果某车底返回车场后须再出场，就必须满足列车整备时间的要求。

本模型以单条城市轨道交通线路为研究对象，已知城轨线路的交路方案、全天的列车运行任务，运行任务的接续时间和地点、车底的使用方式、车底出入段以及整备时间等信息，按照两个运行任务的接续原则，确定所有运行任务的接续方案，将车次任务组合成车次链，在完成全天运行任务接续后，将组合成的若干车次链分配给车底去执行，在分配的过程中，一是要避免车底运用尽量要少，二是尽量均衡每个车底的运用。

2 模型

基本假设如下：1）地铁车辆段和停车场中车底数量充足车底类型相同，编组固定，各车次的时空要素、线路的结构、折返站的折返能力以及车场的布局等基础信息均已知。2）不考虑运营过程中的突发事件应急处置情况，仅研究计划运行图包括的所有运输任务，所有车次严格按照规定的时空要求运行，即在静态条件下编制运用计划。3）所配属的车辆默认为新车，不考虑车底检修等相关问题。4）只考虑各车次间的衔接，不考虑车场与车次间的衔接。5）上下行每个车次的运营里程是相等的。6）列车停站方案均为站站停，因此车底运用计划编制过程中通常避免出现列车越行。

2.1 目标函数

城市轨道交通车底运用问题的初衷是减少运营成本以提高车底利用率，因此，本文主要从降低企业运营成本的角度出发，主要考虑车底固定使用成本和车底接续成本两个方面的运营成本[6]。车底固定使用成本为每个车底运营所产生的固定费用与车底运用数量的乘积；车底接续成本为单位车底接续成本与接续次数的乘积。

此外，车底承担交路段任务的多样性会导致各车底累计运行里程的差异，当各车底累计运行里程差异较大时，即车底运用不均衡时，造成车底不均匀磨耗，会影响车底使用寿命[7]。因此，目标函数还考虑车底运用均衡性，用各车底运用的方差表示车底运用不均衡性，如公式（1）所示。

（1）

式中：Z1为车底不均衡性；l为一个车次的运营里程；为各车底平均运营里程；i， j为第i或第j个车次，i，j∈V=（1，2...V），i≠j；V为单日所有车次任务节点的集合，V={vi|vi=（sio，sid，tio，sid）}；K为共有K个车底，k∈{1，2…K}；当车底k担当车次i和车次j的接续时，xkij=1，否则xkij=0；计算方法为。

对车底固定使用成本和车底接续成本、车底运用不均衡性加权得到多目标函数如公式（2）所示。

（2）

式中：Cij为第i和第j个车次的接续成本；α为每一个车底运营所产生的固定费用；β为车底运用不均衡性的单位费用。

2.2 约束条件

2.2.1 车次接续次数要求

对任意的车次j来说，前续节点和后续节点均是一个车次，或是车场。即所有的车次，最多有一个前续车次与之连接，同时，最多有一个后续节点与之连接。如公式（3）和公式（4）所示。

（3）

（4）

2.2.2 前后节点接续车底相同

对每个车次任务节点来说，其前续节点和后续节点必须由同一个车底来串联，不允许中途更换车底。如公式（5）所示。

（5）

2.2.3 不允许车底空驶运行

所有参与运营的车底，必须承担车次运输任务，至少承担一个车次的运营，不能空驶运行。如公式（6）所示。

（6）

2.2.4 节点接续时空约束

车次任务节点j和车次任务节点i能接续的前提是：j节点的出发车站与i节点的到达车站相同，并且j节点的出发时间与i节点的到达时间之差能满足折返时间的需要。车次任务节点间的接续成本如公式（7）所示。

（7）

式中：sio为第i节点的始发车站；sid为第i节点的终到车站；tio为第i节点的始发时间；tid为第i节点的终到时间；tzf为折返需要的时间；τi为第i车次所在时间段的行车间隔。

2.2.5 回段整备时间约束

如果列车不接续最近的满足折返时间的要求的列车，就默认列车回段整备，需要满足整备作业时间要求[8]，如公式（8）所示。

tjo-tid≥T整备+T回段+T出段，iftjo-tid≥τiandxkij=1，k （8）

式中：T整备为列车整备时间；T出段为列车出段时间；T入段为列车入段时间。

3 案例分析

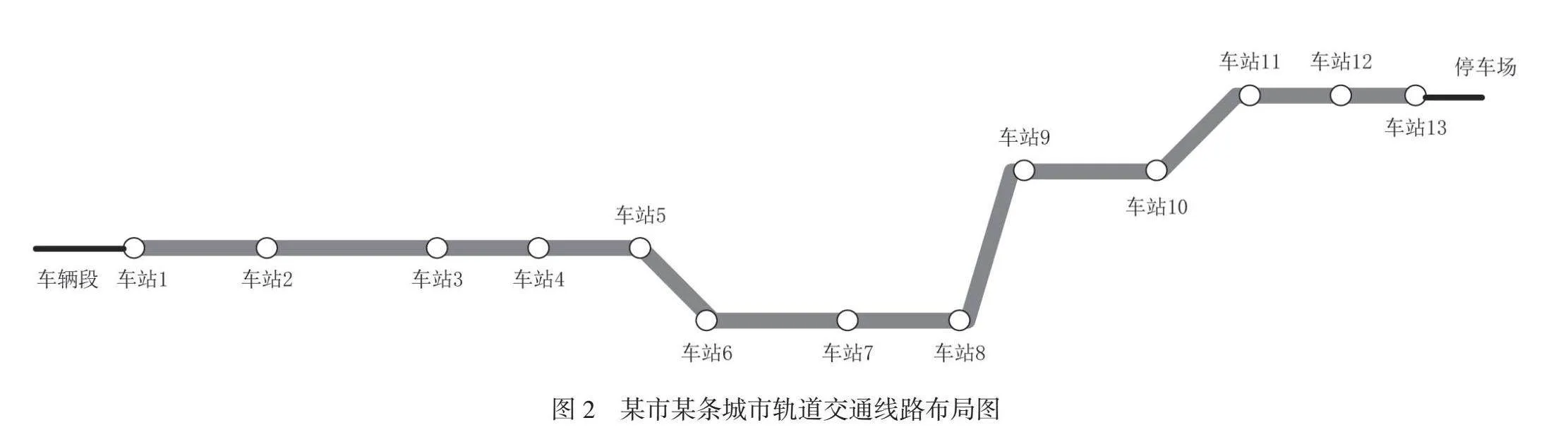
某市新建了第一条城市轨道交通线路，该线路的车站分布情况如图2所示，共13个车站，配备1个车辆段和1个停车场，线路的相关参数见表1。

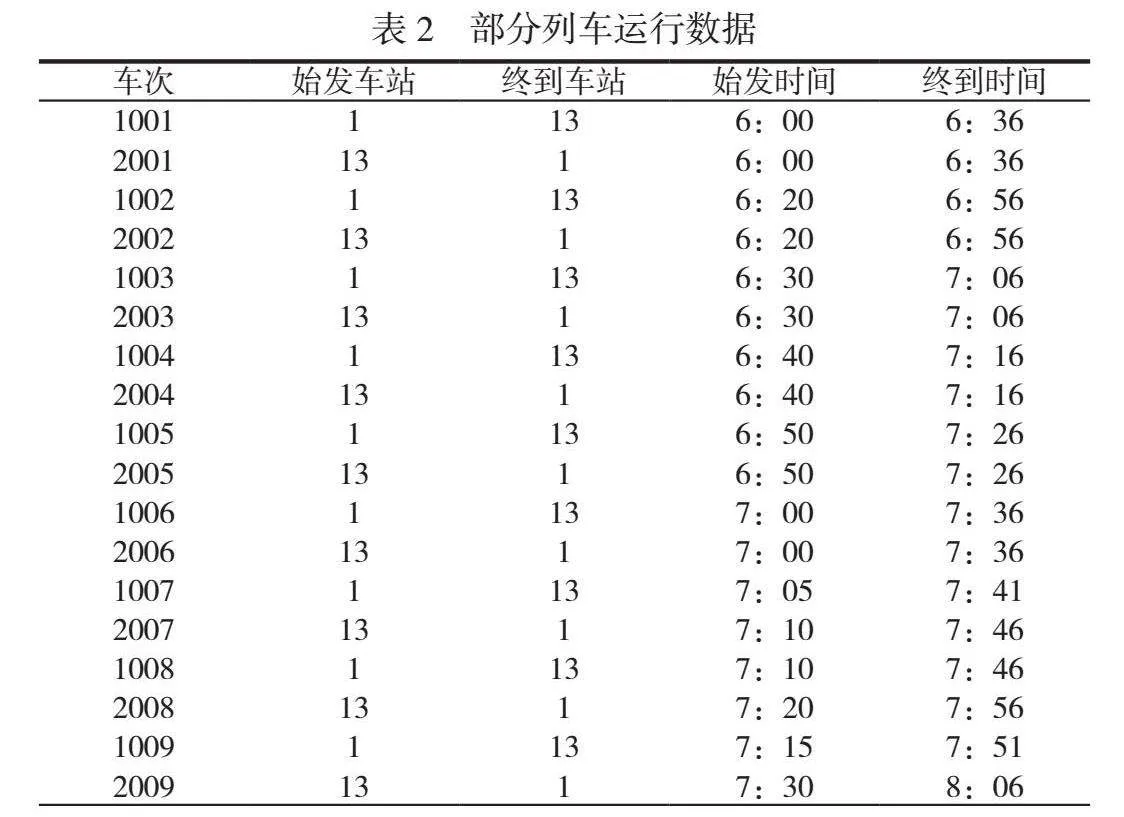
6：00—22：40为线路运营时间，整理列车运行图，得到各车次始发车站、始发时间、终到车站、终到时间等信息，部分列车运行数据见表2。

模型中的参变量取值见表3。

城市轨道交通列车车底运用优化问题属于组合优化问题，当交路段任务较多时，求解难度较大。因此，本文考虑采用启发式算法来求解。求解此类问题常用的启发式算法有模拟退火算法[9]、禁忌搜索算法、蚁群算法等。

从对蚁群算法的现有研究可以看出，由于蚁群算法不但利用了正反馈机制，还采用分布式并行控制，因此发现较优解的能力较强。蚁群算法还具有较好的鲁棒性、优越的分布式计算机制等优点，在解决TSP问题方面效果较为理想，因此，本文选择蚁群算法求解城轨车底运用问题。

表4是部分车底承担的车次任务。需要使用16个车底，接续时间为214min，车底不均衡性为81.73，目标函数数值为190456。

将求解结果代入仿真软件进行仿真验证，结果是可行的，并且接续时间和车底运用不均衡性与计算结果一致。

4 结论

以某条城市轨道交通线路为研究对象，已知基本运行参数及相关设备设施参数，在满足车次接续次数要求、前后节点接续车底相同、不允许车底空驶运行、节点接续时空约束、回段整备时间约束等条件下，使车底数量、接续时间、车底均衡性差距的综合目标最小，建立车底运用计划优化模型。

以某条地铁线路为例，代入相关数据及参数，并通过算法进行求解，得到最优车底运用计划，代入仿真系统，进一步验证模型的可行性和有效性，并将计算结果与该地铁现有的车底运用计划进行对比，得出模型的应用效果。

参考文献

[1]代存杰，李引珍，展宗思，等.考虑动态客流需求和大小交路模式的城市轨道交通列车开行方案优化[J].中国铁道科学，2018，39（2）：128-136.

[2]牛惠民，陈明明，张明辉.城市轨道交通列车开行方案的优化理论及方法[J].中国铁道科学，2011，32（4）：128-133.

[3]姚宇，朱晓宁，康柳江，等.城市轨道交通列车时刻表与车底运用整合优化模型[J].交通运输系统工程与信息，2018，18（1）：200-206.

[4]NIU H M，ZHOU X S.Optimizing urban rail timetable under time-

dependent demand and oversaturated conditions1[J].Transportation Part C，2013，36（11）：212-230.

[5]MENG L，ZHOU X.Robust single-track train dispatching model

under a dynamic and stochastic environment：A scenario based rolling

horizon solution approach[J].Transportation Research Part B，2011（45）：1080–1102.

[6]王世峰.基于动态客流的城市轨道交通列车时刻表与车底运用一体化优化模型和算法研究[D].北京：北京交通大学，2016.

[7]赵冰倩.考虑列车运用均衡性的城市轨道交通车底运用计划优化方法研究[D].北京：北京交通大学，2021.

[8]何必胜，宋瑞，何世伟，等.城市轨道交通车底运用计划编制优化模型求解的混合列生成算法[J].中国铁道科学，2014，35（1）：122-129.

[9]江志彬，徐瑞华，吴强，等.多交路共线运行的城市轨道交通车辆运用优化[J].同济大学学报（自然科学版），2014，42（9）：1333-1339，1431.

指导老师：安飞（1989-）男，汉族，河北交通职业技术学院教师，硕士研究生学历，讲师。

电子邮箱：1312744701@qq.com。