基于GGB的指数函数可视化设计与实践研究

关键词：GeoGebra；指数函数；可视化教学

中图分类号：TP311 文献标识码：A

文章编号：1009-3044（2024）26-0102-03开放科学（资源服务）标识码（OSID） ：

函数教学贯穿着职校数学教学整个过程，是职校数学教学的重点和核心。函数教学可以让学生理解生活处处是数学，数学来源于生活。而指数函数是职校数学教学过程中出现的第一个基本初等函数，也是在研究函数的单调性、奇偶性之后的继而学习的函数。指数函数知识较为抽象，对数形结合要求较高，往往让学生产生畏难情绪。指数函数的学习可以培养学生数学建模意识，提升学生对“数形结合”思想的理解与应用，这对于职校学生是必要的。值得注意的是，职校学生基础相对薄弱，数形结合能力不强，给指数函数教学带来了极大的挑战。

显而易见，数学可视化教学有利于知识呈现、学生接受和师生互动。杨海丽[1]指出可视化方式主要有文本表格、图式和视频等；廖彩云[2]将可视化工具分为外在表征工具和心理表征工具，其中心理表征工具包括背景、故事、模拟实验等通用工具和数学史、数学实验等专门工具；司业佳[3]借助GeoGebra构造了辅助函数教学三个案例，有助于学生概念理解。周后卿、徐幼专[4]将Matlab引入复变函数教学，通过大量的代码，实现了复变函数可视化教学，促进学生对知识的深入理解；李昌志等人[5]运用Matlab和几何画板构建了函数和几何两个模块的教学案例，提升课堂趣味性，引起学生的兴趣，提高课堂效率；努尔色曼·买买提[6]编写了相对应代码，展示了Matlab在函数及其极限中的应用；高芹[7]将GeoGebra贯穿在备课设计、课上设计和测试反馈三个环节，对中职课堂教学优化显著；王荣亮[8]基于GeoGebra的中职数学《函数》全过程可视化设计，克服了职校函数教学的抽象性；张茜[9]将Matlab应用到高等数学原理探究、数值计算和数学三大模块，提升了学生学习效果；袁兰兰[10]利用GeoGebra进行数学问题、数学猜想和数学概念可视化设计，更利于学生理解概念，实现知识迁移。韦美成[11]指出GeoGebra具有功能齐全、操作方便、动态交互、易安装、网上直接使用等优点，也开展了数学教学探究，显著提高了学生的及格率、优秀率。王荣亮[12]将GeoGebra应用到线性规划教学过程中，通过实践表明：GeoGebra的使用可以激发学生学习线性规划的动力，提升学生的操作能力。

可见，Matlab辅助数学教学可视化对编程要求较高，而GeoGebra 具有交互性能，更易于操作。采用GeoGebra辅助教学，呈现指数函数图像绘制过程、指数函数单调性及指数函数图像特征，可深化学生对指数函数的认识，学生对指数函数相关概念、性质与特征理解更直观、更深刻，进一步体会“数形结合”思想。本文通过指数函数中的4个模块展示了GeoGebra辅助职校指数函数教学过程，凸显了GeoGebra的动态功能在教学中的重要作用，为职校数学教学提供一种思路和参考。

1 设计原则

在指数函数可视化案例设计过程中，根据指数函数的教学需要和学生的特点，要充分体现以下4个原则：

1） 注重应用性。数学来源于生活，函数在生活中随处可见。从细胞分裂引出指数函数的基本概念，有利于培养学生应用数学解决实际问题的能力和素养。

2） 体现直观性。在学习指数函数之前，学生对指数函数了解相对较少，而学生对纯粹的代数推导过程和文字呈现往往会产生排斥心理。故而，将函数图像有效地呈现出来让学生通过图像探讨函数的单调性和图像特征，可以加深学生对函数性质和图像特征的理解和记忆。

3） 突出主体性。在教学可视化设计过程中要突出学生主体性的原则。突出学生主体性，就是在教学可视化设计过程中让学生参与教学，与学生产生互动，将课堂交还学生，营造一个学生主动参与、独立思考的环境，培养学生学习知识的兴趣。

4） 强调可操作性。可操作性原则是保证设计的案例能被教师移植、学生参与的一个重要原则。在教学可视化设计过程中，要在保证逻辑性和正确性的基础上，充分考虑案例可被其他教师所用，易于学生接受并参与操作。

2 可视化模块与设计思路

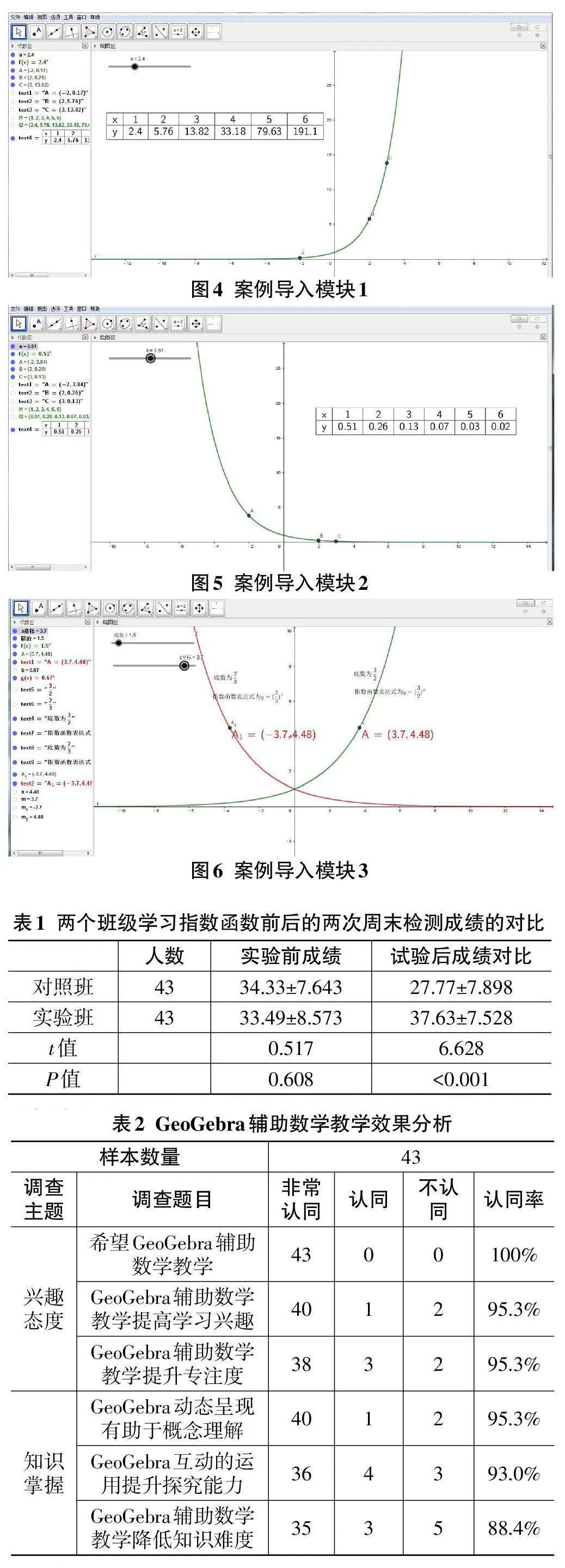
指数可视化模块主要包括案例构建、函数绘制、性质探讨和拓展研究等4部分。其中，案例构建模块主要通过模拟单个细胞分裂过程，让学生对指数式增长有个直观的感受。函数绘制模块以单细胞分裂过程中的指数函数y=2^x为例，通过取值、描点、连线等步骤绘制出函数图像，引导学生复习函数绘制的三个基本步骤。性质探讨模块通过改变参数，绘制不同底数的指数函数，引导学生观察不同底数指数函数的单调性、定义域和值域等函数的基本性质。拓展模块通过绘制底数互为倒数的指数函数，观察每对指数函数的图像之间关系，引导学生归纳出指数互为倒数指数函数的图像特征。可视化模块和设计思路如图1所示。

3 可视化案

例指数函数教学可视化案例主要包括案例构建、函数绘制、性质探讨和拓展研究等模块。

3.1 案例构建模块

案例构建模块主要以细胞分裂为模型。如图2所示，滑动条i 取值范围为1～6，每次增加步长为1。通过拖动滑动条，改变滑动条i 的取值；文本表格中x显示的是分裂的次数，y显示的是经过x 次分裂后细胞的个数。例如滑动条i=1时，x=1，y=2，代表细胞分裂1 次，得到2个细胞，而当滑动条i=6时，x=1，y=2，代表细胞分裂6次，得到64个细胞。

在细胞分裂过程中，学生可以参与计算经过分裂i 次后的细胞，并根据模拟的动态过程直观感受到细胞分裂过程中细胞个数以2x形式增长，增长的速度很快。模拟细胞分裂可以激发学生学习动力，培养学生探究精神。

3.2 函数绘制模块

函数绘制模块主要复习绘制函数图像的3个基本步骤：取值、描点、连线。如图3所示，函数绘制模块以案例导入中细胞分裂次数和个数为坐标点，然后在绘图区2中描出对应的坐标点，再进行连线。通过函数绘制模块，学生可以回顾和巩固绘制函数图像的3个基本步骤。

3.3 性质探讨模块

性质探讨模块主要讨论不同底数情况指数函数图像的基本性质。如图4和图5所示，本模块主要分为底数大于1和底数在0和1之间两种情况。

图4中，滑动条a 的取值范围设置为1.1～6，每次增加步长为0.1。通过拖动滑动条a，可以观察到指数函数图像在底数大于1情况下函数的图像。观察函数图像后，引导学生总结底数大于1情况下指数函数的定义域为全体实数、值域为（0，+∞）、单调性为单调递增函数，且底数越大函数图像也抖，增长速度越快。

图5中，滑动条a 的取值范围设置为0.1～0.9，每次增加步长为0.1。通过拖动滑动条a，可以观察到指数函数图像在底数在0和1之间的函数的图像。观察函数图像后，引导学生总结底数在0和1之间指数函数的定义域为全体实数、值域为（0，+∞）、单调性为单调递减函数，且底数越小函数图像越抖，减少速度越快。

3.4 拓展研究模块

拓展研究模块主要研究底数互为倒数的一对指数函数的图像特征。如图6所示，滑动条底数a 的取值范围为1.1～9，每次增加0.1个步长；变量b 设置为底数a 的倒数；A点x 坐标亦采用滑动条，并在图中绘出点A（x，a^x）和点A1（-x，b^x）。通过观察绘制底数互为倒数的一对指数函数图像，以及A和A点之间的关系可以发现当底数互为倒数的一对指数函数的图像关于y轴对称。

4 实践效果分析

为了分析GeoGebra辅助指数函数教学效果，讨论GeoGebra是否可以激发和提升职校学生对学习数学的兴趣，增强职校学生学习数学的动力，选取j2O/QuzA13bqqgQJuHTkcolKYGn1m2W4zj/jHAneQ1Q=了宿迁科技学校两个平行班，一个为实验班，一个为对照班。实验班的教学老师教学过程中采用GeoGebra辅助指数函数可视化教学模块，而对照班主要采用传统的以粉笔和黑板为主导的授课方式。

对比两个班级学习指数函数前后的两次周末检测成绩（满分为50分），如表1所示。两个班级在实验前成绩没有显著差异，但是经过实验过后可以发现实验班相对对照班成绩有较大差异。这说明GeoGebra 辅助数学教学相较于传统的板书式授课方式更有利于学生对数学知识的吸收和掌握。

对实验班的43名学生进行问卷调查，问卷内容包括2个主题，6个选择题，回收有效问卷43份，统计结果如表2所示。调查结果显示100%的学生希望使用GeoGebra辅助职校数学教学，95.3%的学生认为在职校数学教学过程中GeoGebra使用可以提高学习兴趣，95.3%的学生认为在职校数学教学过程中GeoGebra 的使用有助于学生自身专注度的提升，95.3%的学生认为在职校数学教学过程GeoGebra的动态呈现功能可以帮助对概念的理解，93%学生认可在职校数学教学过程采用GeoGebra以增加互动性并认为这样可以提升学生的探究能力，88.4%的学生认为职校数学教学过程中GeoGebra的使用可以降低知识难度。有助于学生对知识的掌握。

综上，在职校数学教学过程中采用GeoGebra，有助于学生对概念的理解、激发学生学习兴趣、夯实学生知识基础。

5 小结

指数函数是职校数学课程中首先接触到基本初等函数，具有一定的实际应用背景，也关乎学生对函数性质的把握和理解，对数形结合要求也相对较高，在教学过程中应理论性和实践性相结合。GeoGebra 强大的绘图功能和动态呈现功能，有助于指数函数教学的可视化，降低知识难度，帮助学生更好地理解概念，提升学生对数学的兴趣，培养学生的探究能力。在职校数学教学实践过程中，应当不断拓展其应用，更好地提高教学质量。