水下圆柱体声学隐身斗篷性能研究

摘" 要： 水下环境下声学隐身斗篷的发展对潜艇隐身能力的提升具有重要意义，基于水的密度、声速和体积模量为出发点设计了圆柱体水下声学隐身斗篷及其分层模型，研究其在500～3 500 Hz范围内圆柱体外周声场特征和隐身性能.研究发现随着隐身层厚度和频率的增加，隐身层内部区域靠近刚性圆柱体的部分出现了零声压区域，导致有效隐身厚度变小.通过增加隐身层厚度来实现高隐身性能的设想在高频率下并不一定成立，但可以延迟零声压区域的出现，巩固隐身层的有效厚度，高频区间则应增加隐身层层数.在3 500 Hz频率时，随着声学隐身斗篷层数的增加，实际是减小其散射声压幅值，周期性也更加明显，从而导致总声压偏离背景声压的区域变得更小，隐身能力得到增强.通过对水下圆柱体隐身性能的研究，有效给出了较大频率范围内声学斗篷隐身能力提升的方向.

关键词： 潜艇；声学斗篷；隐身性能；散射声压；声场分布

中图分类号：U674.76""" 文献标志码：A""""" 文章编号：1673-4807（2024）05-023-09

DOI：10.20061/j.issn.1673-4807.2024.05.004

收稿日期： 2023-05-02""" 修回日期： 2021-04-29

基金项目： 江苏省高层次创新创业人才引进计划项目（JSSCBS20211001）；江苏科技大学科研启动基金项目（1012932009）

作者简介： 熊仲营（1985—），男，博士，讲师，研究方向为水声工程、多目标优化设计.E-mail： xzying117@just.edu.cn

引文格式： 熊仲营，叶仁传.水下圆柱体声学隐身斗篷性能研究［J］.江苏科技大学学报（自然科学版），202 38（5）：23-31.DOI：10.20061/j.issn.1673-4807.2024.05.004.

Study on acoustic cloaking performance of underwater cylinders

XIONG Zhongying1， YE Renchuan2

（1.School of Naval Architecture amp; Ocean Engineering， Jiangsu University of Science and Technology， Zhenjiang 212100， China）

（2.Ocean College， Jiangsu University of Science and Technology， Zhenjiang 212003， China）

Abstract：According to the significance of cloaking of submarine， an underwater cylindrical acoustic cloak and its layered model are designed based on the density， sound velocity and volume modulus of water in this paper. The acoustic field of the cylinder and acoustic cloaking performance are studied at 500～3 500 Hz. It is found that with the increase of its thickness and operating frequency， a region of zero sound pressure appears in the inner region of the structure of acoustic cloak near the cylinder， which leads to the decrease of effective cloaking thickness. The idea of achieving high acoustic cloaking performance by increasing the thickness of cloaking structure is not necessarily valid at high frequency， but it can delay the appearance of zero sound pressure region and consolidate the effective cloaking thickness. Good acoustic cloaking performance should increase the number of layers at high frequency. At 3 500 Hz， with the increase of the number of acoustic cloaking layers， the scattered sound pressure amplitude becomes smaller and the periodicity becomes more obvious. As a result， the region where the total sound pressure deviates from the background sound pressure becomes smaller and the cloaking performance is enhanced. According to the analysis results， the direction of improving the cloaking performance of acoustic cloak in wider frequencies is given effectively.

Key words：submarine， acoustic cloak， acoustic cloaking performance， scattered sound pressure， acoustic field distribution

为了降低潜艇的声目标强度并凸显其突发攻击能力和隐蔽性，潜艇声学隐身技术的发展成为了不可回避的问题.然而随着声呐探测技术的进步［1］，潜艇高隐身性能仍需要满足在更大的频域范围内实现声学隐身，因此对于新型潜艇声隐身技术的探索和研究仍受到了国内外学者的青睐.文献［2］基于奇异变换理论设计了一种电磁隐身衣实现了物体在电磁场中隐身的效果，后经证实电磁波变换方法可适用于二维声波方程，从而促进了声学变换理论的发展.目前，潜艇超材料隐身技术是一种非常重要的隐身技术，仍在现有隐身技术层面处于前沿阵地［3］.声学隐身潜艇覆层超材料其实是一种声学负折射率材料，制备工艺主要是对特定材料进行微观工程结构层面上的加工.这种方法主要是采用了声学变换理论对于隐身材料层须具有各向异性的要求，从而使超材料覆层实现声波无法进入隐身区域而发生弯曲.目前，超材料在空气介质中的声学隐身已取得了较大的进步，然而对于水下环境的声学隐身仍有较大的进步空间［4］，特别是对于较大频域范围内的声学隐身性能的探索.声学隐身斗篷就是一种在水下环境中的各向异性声学隐身超材料，它主要是通过操控声波传播路径从而实现声波绕射来达到减弱声波散射的目的，从而实现声学隐身.然而，声学隐身斗篷受限于制备工艺等客观条件，无法实现在空间上物性参数的连续性，转而采用分层制备的方式达到近似的效果，但也不同程度地影响了其声学隐身性能［5］.文献［6］提出了一种双层（超表面+零折射率超材料）声传递混合斗篷壳，并表示可用于空气介质中和水下超声波的声透射.文献［7］采用了非线性转换斗篷（分层、均匀化和各向同性材料）验证了在无粘流体中宽带圆柱壳斗篷的声传递特性，并总结了相对于传统线性转换斗篷的优缺点.文献［8］基于坐标转换法提出了一种区域划分和多原点坐标转换法声学斗篷设计方法，通过对弧形斗篷的设计结果发现该方法有效控制了声波传递并降低了声压级.文献［9］通过改变亥姆霍兹方程的坐标设计并验证了一些各向异性非均匀超材料，通过数值模拟的方法定性和定量地研究了这些超材料的隐身效率.文献［10］基于桁架晶格模型设计了一种椭圆五模声学斗篷，并通过数值仿真验证了其具有良好的波隐藏功能.文献［11］设计了一种水下声学隐身自适应斗篷，它主要是通过对一种泊松比为-1的软性超材料进行自动变形，从而被动满足隐身设计中的准保角映射.文献［12］提出了一种二维声子晶体的隐身结构，该结构可通过改变单元尺寸和填充因子来改变工作频率，并且声子晶体具备负折射和自准直的协同作用，从而实现了隐身的目的.文献［13］认为当前声学超表面的一个严重的限制仍然是其适度的可调性，以满足多频率和可调节功能需求.

目前，声学隐身技术和超材料的发展对于潜艇隐身能力的提升是有积极意义的.此外，对于声学隐身机理和较大频域范围内隐藏体外声场分布的探索对于潜艇声学隐身斗篷的开发具有指导意义.考虑到水下潜艇的外形特征，此处将其简化为圆柱体结构.而对于推进系统性质干扰噪声，一般体现在高频段.因此，文中基于水下环境下一种声学隐身斗篷及其分层模型，研究其在500～3 500 Hz范围内圆柱体外周声场特征和散射声波变化规律，从而确定其声学隐身性能.

1" 计算模型及研究方法

1.1" 计算模型

声学变换理论的基本原理是基于Helmholtz方程的形式不变性，将不同空间之间的坐标建立对应变换关系X=f（X′），进而求出物性参数的变换，得出Helmholtz方程在新空间区域的表达方程.如果设定隐身斗篷的声波波线的坐标变换效果，根据声学变换理论映射变换前后的波线位置坐标，从而实现声学隐身效果.由于掩体形态的不同，采用声学转换理论可以设计不同隐身层的材料参数.文中选取的圆柱体具有高度的对称性，可采用线性点变换方法设计隐身层，由初始空间中一点向外扩大，扩展区域即圆形隐身层区域.圆柱体掩体外表面相当于初始扩张点，向外扩张即形成环形隐身层，因此必须从圆形空间区域（半径为R）转换到环形隐身层空间区域（内外半径分别为R1和R2），并形成环形隐身层物性参数的转换.二维圆柱坐标系下，其坐标变换关系为：

r（θ）=f（r′）=R2－R1R2r′（θ′）+R1（1）

θ=f（θ′）=θ′（2）

式中，r′（θ′）和r（θ）分别为圆形区域和环形隐身层的半径（角度）.两个区域在极坐标下的Helmholtz声学方程分别为：

SymbolQC@ 1ρ（r′，θ′）

SymbolQC@ p（r′，θ′）=－ω2κ′（r′，θ′）p（r′，θ′）（3）

SymbolQC@ 1ρ（r，θ）

SymbolQC@ p（r，θ）=－ω2κ（r，θ）p（r，θ）（4）

对于圆柱体隐身层，其密度需满足非均匀各向异性，而体积模量为非均匀各向同性，实现了声学隐身的材料基础.两个区域的密度和体积模量变换关系为：

ρ（r，q）-1=r′（r，q）-1AATdet A（5）

k（r，q）-1=k′（r，q）-1det A（6）

式中，Jacobian矩阵A可表示为：

A=（r，θ）（r′，θ′）=R2－R1R200r′r′-R1R2－R1R2（7）

代入式（5、6）后可得：

ρ=ρr00ρθ=ρbr′－R1R200r′－R1r′1（8）

κ=κbr′r′－R1R2－R1R12（9）

式中：ρb和κb为分别为外部流域介质的密度和体积模量.从式（8）可以看出，当r′→R1时，ρr→∞且ρθ→0.因此，在隐身斗篷的内边界存在仅有的奇点，而在内边界外侧物性参数满足连续性.

变换声学理论是指将不同空间之间的坐标进行转换，从而建立不同空间之间的物性参数的变换关系.然而，声学隐身层的物性参数是连续、非均匀且各向异性的，同时隐身斗篷内边界密度的奇异性也对隐身层的实现提出了较高的现实材料要求，因此无法直接制备.在研究和处理非均匀材料过程中，沿其非均匀方向进行合理近似离散是可取的，并且离散后在内边界处将不存在奇点.根据等效介质理论，各向同性的等效介质A和B进行多层交替组合可等效出环形隐身层壳，这就是分层制备的基本原理，其物性参数离散后满足：

ρr=δρA+（1－δ）ρB（10）

ρθ=δρ－1A+（1－δ）ρ－1B（11）

K－1=δK－1A+（1－δ）K－1B（12）

其中，δ=nA/（nA+nB），nA、nB分别为各自的层厚.如果δ→0或 那么越靠近掩体壁时的材料A或B必须具有较低的密度或较高的密度.由于水密度较大，与空气介质相比水环境下可以较为容易地获得低密度层，但获得高密度层却相对困难.为了降低对材料密度的苛刻要求和分层制备工艺的相对简易化，文中选取了δ=0. 即等效介质A或B具有相同的厚度.

每一个离散层（N）中，等效介质A和B的物性参数满足：

ρA（r′）=ρr（r′）+ρ2r（r′）－ρ2b（13）

ρB（r′）=ρr（r′）－ρ2r（r′）－ρ2b（14）

1K（r′）=121KA（r′）+1KB（r′）（15）

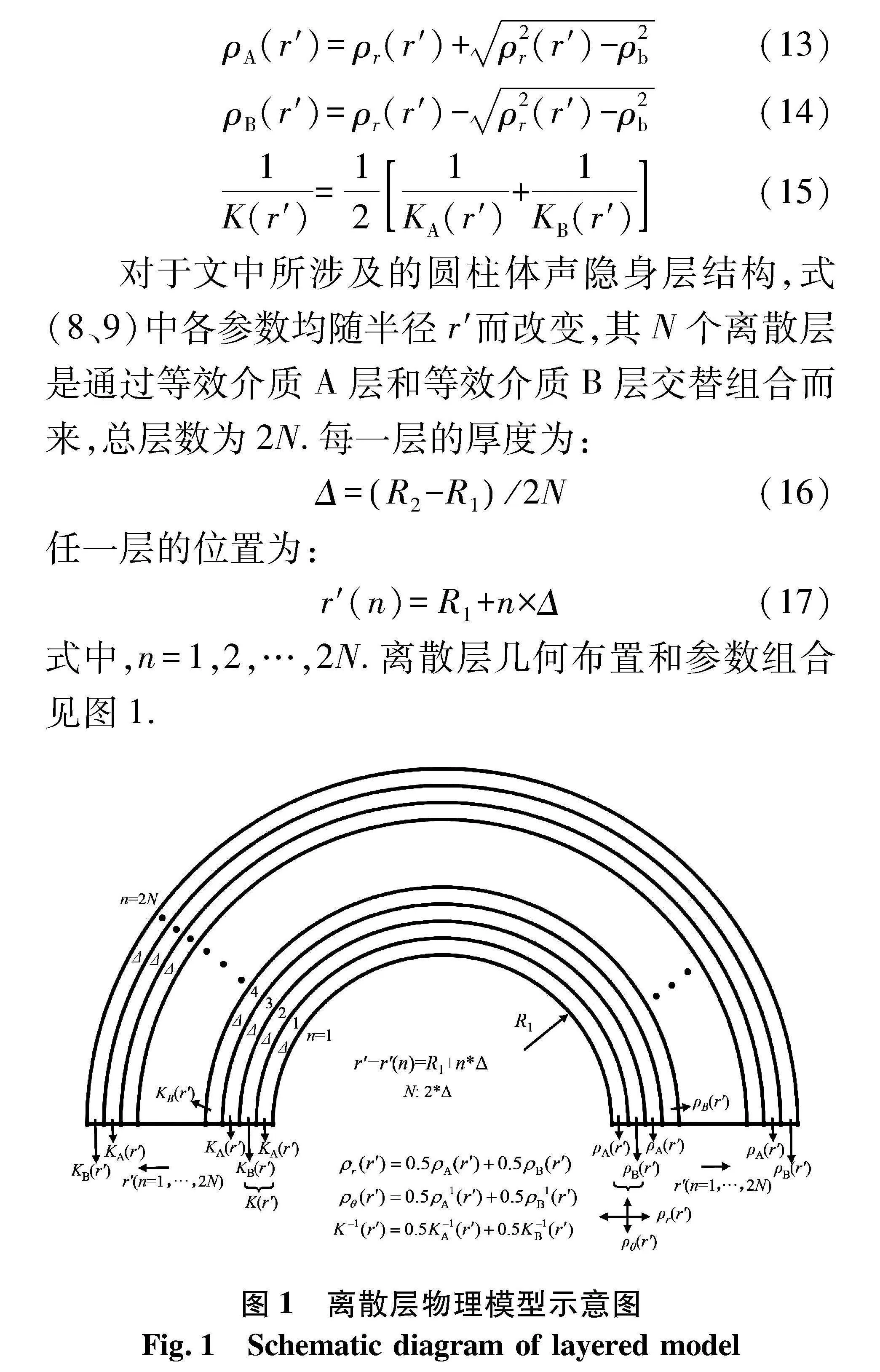
对于文中所涉及的圆柱体声隐身层结构，式（8、9）中各参数均随半径r′而改变，其N个离散层是通过等效介质A层和等效介质B层交替组合而来，总层数为2N.每一层的厚度为：

Δ=R2－R1/2N（16）

任一层的位置为：

r′（n）=R1+n×Δ（17）

式中，n=1，2，…，2N.离散层几何布置和参数组合见图1.

为了尽可能地实现物性参数的连续、非均匀和各向异性，需要在极限化的条件下完成，选取50层斗篷模型（2N=50）和20层斗篷模型（2N=20）来近似等效声学隐身层，并分析在不同等效层的影响下水下圆柱体的隐身性能.

文中采用有限元软件COMSOL Multiphysics对不同隐身斗篷和无隐身斗篷模型进行计算分析，计算模型如图2.计算模型分为均匀化斗篷、无隐身斗篷、50层斗篷和20层斗篷模型，分别对应图2左上、右上、左下和右下模型，斗篷外接水域.由于圆柱体的几何镜像对称性，计算模型采用了完整几何的一半.对于圆柱体隐身层，R1为圆柱体外表面的半径（即隐身斗篷的内半径），R1=1 m.R2为隐身斗篷的外半径，R2=2×q0（m），q0为斗篷层厚系数，表征了斗篷的相对厚度，文中q0分别为0.75、1.00、1.25.

其中，50层斗篷模型和20层斗篷模型是通过两种等效介质层（等效介质A和B）交替布置的方法来等效成声学隐身层，20层斗篷模型等效介质布置如图3.依据方程式（16～17），不同计算模型中的隐身层参数如表1.

1.2" 数值计算方法

对于50层斗篷模型和20层斗篷模型，第i层的对应的等效介质A或B对应的密度分别为ρA（i）或ρB（i），声速cA（i）或cB（i），有效体积模量KA（i）或KB（i），分别表示为式（18～22），K0为隐身层外部介质的体积模量，rA（i）或rB（i）为等效介质层半径，R1≤rA（i），rB（i）≤R2.其中，ρb和cb为分别为水域的密度和声速，取值为1 000 kg/m3和1 500 m/s.

ρA（i）=ρbrA（i）rA（i）－R1+ρbrA（i）rA（i）－R12－1（18）

i=1， 2， 3， …， 2N，2N=50或2 下同.

ρB（i）=ρbrB（i）rB（i）－R1－ρbrB（i）rB（i）－R12－1（19）

cA（i）=cB（i）=R2－R1R2r（i）r（i）－R1cb（20）

KA（i）=K0R2－R1R22rA（i）rA（i）－R1（21）

KB（i）=K0R2－R1R22rB（i）rB（i）－R1（22）

对于任何周期体系，体积模量（在均匀化极限下）不依赖于晶格的类型（各向同性或各向异性）.因此，有效体积模态和有效密度可以通过求其倒数的体积平均值来确定［14］.对于在均匀化极限条件下等效介质A和B组成的单层均匀化斗篷，其切向（沿层向）有效体积模量和有效密度分别定义为：

K=2KAKBKA+KB（23）

ρt=2ρAρBρA+ρB（24）

而均匀化斗篷其法线方向（垂直于层）的有效密度可采用其体积平均值，定义为：

ρn=ρA+ρB2（25）

此时，方程式（23～25）中的参数均为方程式（18～22）消除了下标（i）所得，其隐身层半径满足条件：

rA（i）=rB（i）=r（i）=r（26）

均匀化斗篷的有效密度张量ρ为：

ρ=ρn00ρt（27）

因此，均匀化斗篷密度满足密度各向异性特征.

低频时，声波波长大于或者与航行器尺度具有相同数量级时，固壁（含隐身层）结构对声波波动的影响较小.但随着频率的增加，声波波长逐渐小于航行器尺度，固壁（含隐身层）结构将变成非紧致结构，其散射声场将变得更为突出.在研究斜入射水下夹芯复合材料的吸声系数和反射系数时［15］，发现入射声频率很低时，吸声层厚度远小于波长，如同吸声结构不存在一样，而在5 kHz以上时反射系数和吸声系数随频率起伏较小.而水下声速相较于空气介质更高，更加助长了这一趋势.文中选取求解f=500～3 500 Hz时压力声学频域亥姆霍兹方程：

SymbolQC@ ·（－ρ－1

SymbolQC@ pt）－ω2ptK=0（28）

式中：ρ为各向异性材料的密度张量；pt为总声压，包含了背景声压pb和散射声压ps，为：

pt=pb+ps（29）

入射波为沿x方向向右传播的入射平面波，其背景场pb定义为：

pb=e－ikbx（30）

其中，kb=2πf/cb为背景介质中的传播常数.背景介质在其外部边界上采用柱面辐射条件进行截断，圆柱体表面设定为硬声场边界条件.从式（18～28）可以看出，文中所述的声学隐身层的物性参数是基于水的密度、声速和体积模量为出发点设计出来的，虽然目前大量研究都证实了隐身衣在低频领域的隐身性能，但对于中高频等较大频域范围内的声学隐身性能及特点仍存在较大的探索空间，特别是在水下环境中.

为了验证数值计算的正确性，首先模拟了文献［16］中涉及空气介质下的隐身性能.其数值模型采用多了多层隐身层结构，此处选取了kb=10时的数值模型，b为隐身层的厚度，b=1.0 m；k为波数，相应的声波频率为280 Hz.图4显示了在50层隐身层（第二行左图）下总声压场的计算结果，通过与文献［16］对比可以发现其总声压场分布规律完全相同.此时，圆柱体的散射截面积为3.518 7×10-5 m 也和文献［16］中接近零的结论相符合.散射截面积σ定义为：

σ=2πlimr→

SymboleB@ rpspb2（31）

此外，从无隐身模型→20层斗篷模型→50层斗篷模型的计算结果可以看出，其总声压场逐步趋向连续均匀化斗篷模型，这符合物理规律，也再次验证了模拟的有效性.

1.3" 网格敏感性验证

为了验证数值模型的网格敏感性，文中采用水下圆柱体在（200～500 Hz）范围内的均匀化斗篷模型进行研究，选取了隐身层外周与x轴相交的检测点（标示在图2中）的总声压进行对比分析，其计算结果如图5.网格共进行了5次划分，采用了结构化扫描网格，其最大单元大小分别设定为c/f/6、c/f/8、c/f/12、c/f/16、c/f/2 此时的c指的是水下声速，为了统一标准，f=3 500 Hz.通过计算结果可以看出，随着网格不断细化，检测点的总声压基本保持不变，从而验证了数值模拟满足网格敏感性要求，并选取了最大单元大小c/f/20数量级用于分析500～3 500 Hz频率范围内水下圆柱体外围的声场.

2" 数值结果及分析

2.1" 总声压分布

通过对比在500～3 500 Hz频率范围内的声压场变化规律，文中选取了1 000 Hz作为该频率范围内的研究频率步长.图6为不同隐身斗篷模型（q0=0.75、1、1.2 下同）在500～3 500 Hz频率范围内水下圆柱体外围总声压.对于无隐身模型，刚性圆柱体的散射效应较强，波性阵面波动明显.在入射波频率为500 Hz时，50层斗篷、20层斗篷和均匀化斗篷模型的波形阵面几乎是一致的.随着频率的增加，圆柱体后方均出现不同程度的影区，且总声压逐步趋于零.同时，波形阵面在刚性圆柱体附近略有改变，但影响程度并不大.当加上20层隐身斗篷后，随着频率的增加，圆柱体后方也逐步出现影区.同时，在圆柱体的后侧和前侧中部均出现不同程度的波形阵面错移的情况，且随着频率的增加，阵面甚至出现了断裂.而50层斗篷在隐身层厚度和频率增加到q0≥1和2 500～3 500 Hz的计算区域内也出现了阵面错移的情况，且越来越严重.随着隐身层厚度和频率的增加，隐身层内部区域波形阵面受到了刚性圆柱体辐射的作用而出现弯曲，且隐身层越厚，弯曲越平缓，并在斗篷边界处和外部波形阵面达到相同声压水平，从而实现了声学隐身.相对于分层模型，均匀化斗篷在计算区间内并没有出现影区和阵面变形的情况，入射波绕射后继续向前传播，即使是q0=0.75的较小隐身层厚度下圆柱体外围的阵面弯曲也迅速在隐身层内部区域内得到了恢复，说明其声学隐身效果较好.随着隐身等效层越来越密，其隐身效果也越好.

对比50层斗篷和20层斗篷，由于隐身层离散程度的不同，20层斗篷隐身层内部区域波形阵面不仅仅出现了弯曲，而且随着频率的增加，阵面界限变得越来越混乱，甚至在隐身层内部区域靠近刚性圆柱体的部分出现了零声压区域.这些零声压区域和圆柱体后方的影区特征相似，且随着频率和隐身层厚度的增加，零声压区域的面积也增大.这些零声压区域似乎不符合随着隐身层厚度增加隐身效果越好的结论，并且随着隐身层厚度和频率的增加，20层斗篷的隐身层有效厚度也越来越小，但斗篷边界的波形阵面却明晰可见，似乎刚性圆柱体的外径扩宽到了零声压区域的边界.而50层斗篷在q0≥1和2 500～3 500 Hz的计算区域内隐身层也逐步出现阵面界限越来越混乱的情况.因此，随着隐身层厚度和频率的增加，通过增加隐身层厚度来实现高隐身性能的设想并不一定成立，但可以实现延迟零声压区域的出现，巩固隐身层的有效厚度.上述情况的产生是因为在隐身层物性参数无法实现连续、非均匀且各向异性的条件，分层制备也无法实现极限化条件.

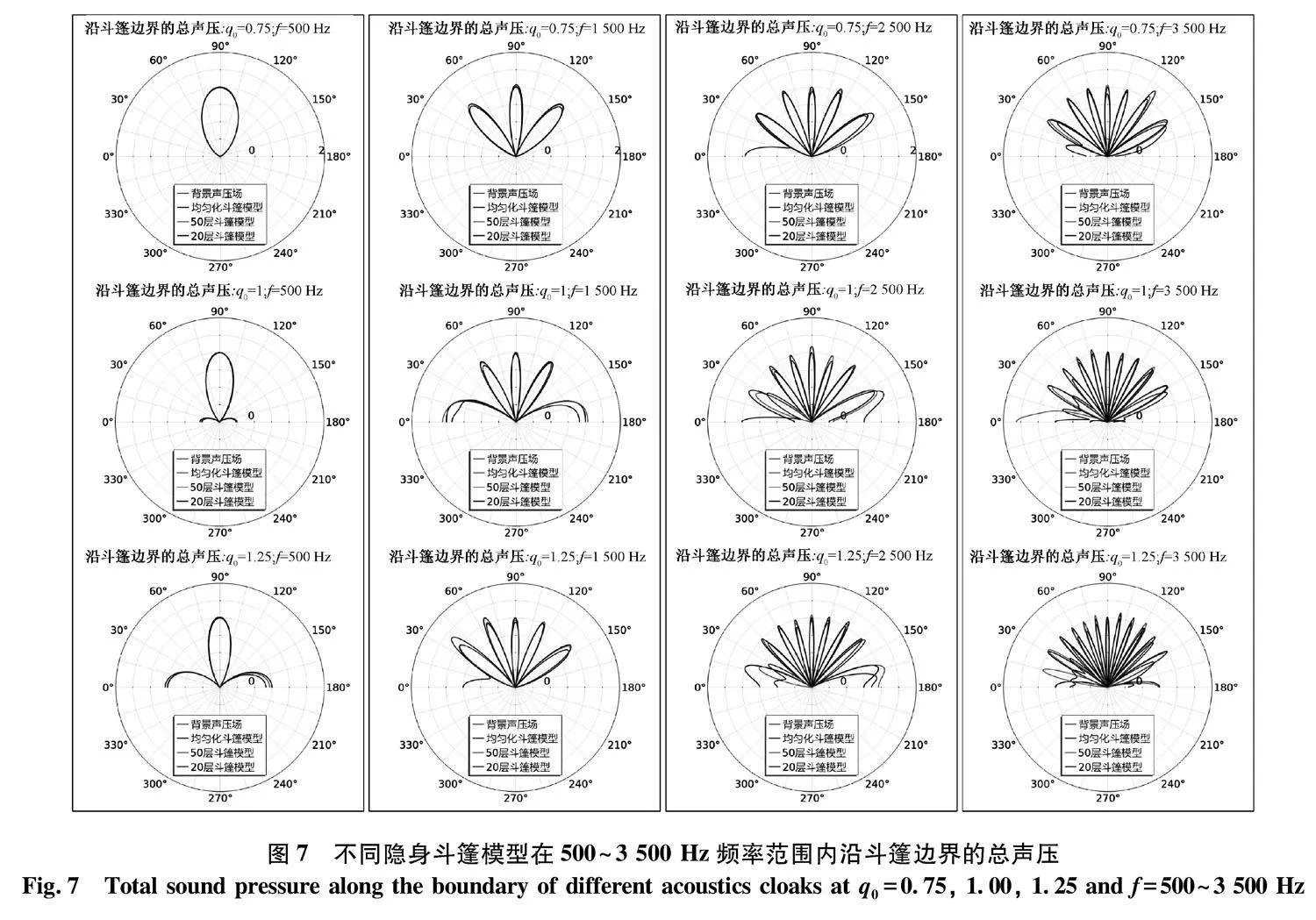
2.2" 沿斗篷边界声压分布

为了更好地隐藏水下圆柱体，其散射效应越小，斗篷外边界处附近的波形阵面和入射波越接近，其隐身层效果就越好.为了进一步检验不同模型和频率下的声学隐身性能，选取斗篷边界上的声压进行分析.图7为不同隐身斗篷模型在500～3 500 Hz频率范围内沿斗篷边界的总声压.随着频率的增加（波长变短），斗篷边界的声压也随着横跨波形阵面的波数增多而表现出更大的波动性，其中均匀化斗篷边界声压和背景声压场贴合较好.此外，频率的增加也导致了20层斗篷边界总声压在圆柱体的入射侧多出了半个周期、1个周期甚至更多周期的波动性，且越贴近角度为0的区域振幅也变得越小.50层斗篷也在更高的频率下出现周期性分离和振幅的偏离.随着层数的增加，50层斗篷模型的斗篷边界总声压比20层斗篷模型更加贴近于均匀化斗篷模型，这符合近似离散分层制备的基本原理.但是，随着频率的增加，50层斗篷模型也逐步偏离均匀化斗篷模型，这是由于在相对较高的频率下，层厚波长比越大，近似离散也越差，应该继续细化分层才能实现更好的近似效果.隐身层越厚，50层斗篷和20层斗篷入射侧的边界声压波动偏离入射波的区域更大，振幅也更小，其余区域也出现了不同程度的偏离于背景声压.这再次说明了增加隐身层厚度并不一定能增强隐身斗篷的隐身性能，相反可能导致其波动程度更加明显，很可能与其隐身层有效厚度降低有关.两种分层斗篷边界声压周期性波动和入射波声压波动性的背离与散射声压的分布有直接的关系，振幅变小也同样与散射声场有关，特别是在高频率3 500 Hz下显得尤为明显.

图8显示了不同隐身斗篷模型在3 500 Hz频率时沿斗篷边界的声压分布，包含了总声压、背景声压和散射声压.从图中可以看出，无斗篷边界总声压和散射声压的振幅波动均较大，且散射声压的周期性较差.而20层斗篷模型的散射声压在圆柱体入射侧和后侧均有较大的振幅，此时背景声压相位和散射声压相位错开，从而导致了总声压振幅较小.另外，在60°和120°的区域内散射声压振幅却较小，从而导致总声压和背景声压贴合的较好.在50层斗篷模型中，30°～180°的区间内，斗篷边界散射声压振幅较小，且周期性也较好，从而使总声压在绝大部分区间和背景声压贴合的更好.仅仅在q0=1时圆柱体的入射侧0°～30°区间内有较大散射声压而导致总声压的大幅度增加，而在q0=1.25时由于散射声压的波峰和背景声压的波谷相叠加，导致了总声压基本维持在整个区间的同一水平，但相位却偏离于背景声压.在3 500 Hz频率时，随着隐身斗篷层数的增加，实际是减小其散射声压幅值，周期性也更加明显，从而导致总声压偏离背景声压的区域变得更小.

散射声压的周期性分布与幅值和隐身斗篷模型的近似离散程度有较大的关系.相较于20层斗篷模型，层数更多的50层斗篷模型的散射声压周期性分布更为明显，振幅在大部分区域也相对维持在零声压附近波动.但在入射侧的高振幅也说明了隐身层改变了散射声压的辐射指向性，使散射声压的声压值和相位均有所偏移，这是由于有限离散分层模型无法实现物性参数的连续性.而随着隐身层厚度的增加，入射侧的散射声压幅值均有不同程度的增大，且影响区域也随层数增加表现出逐步变小的趋势，但也造成了总声压在入射侧偏离于背景声压，这验证了上述关于散射声压对斗篷边界总声压周期性波动和偏离有关系的结论.对于均匀化斗篷，其散射场声压基本为 总声压和背景声压完全贴合，这也证实了在水下环境下文中所采用的物性参数连续、非均匀和各向异性的均匀化隐身斗篷模型的理想隐身能力，也间接验证了设计的圆柱体水下声学隐身斗篷模型的正确性.

通过上述的分析可以看出，20层斗篷模型和50层斗篷模型分别在flt;2 500 Hz和flt;3 500 Hz的范围可实现较好的隐身效果，但随着隐身层厚度的增加，其隐身性能都随之降低.均匀化隐身斗篷模型在500～3 500 Hz范围内则具有理想的隐身能力.为了增加隐身斗篷在高频区间的隐身能力，应增加其隐身层层数，同时选择合适的隐身层厚度.

3" 结论

基于水的密度、声速和体积模量为出发点设计了圆柱体水下声学隐身斗篷及其分层模型，研究其在500～3 500 Hz范围内圆柱体外周声场特征和散射声波规律，从而确定其声学隐身性能.通过对水下圆柱体隐身性能的研究，文中的结果有效给出了较大频率范围内声学斗篷隐身能力提升的方向.

（1） 随着隐身层厚度和频率的增加，声学隐身斗篷分层模型的有效隐身厚度也越来越小，似乎刚性圆柱体的外径扩宽到了零声压区域的边界.通过增加隐身层厚度来实现高隐身性能的设想在高频率下并不一定成立，但可以实现延迟零声压区域的出现，巩固隐身层的有效厚度.

（2） 声学隐身斗篷边界声压周期性波动和入射波声压波动性的背离与散射声压的分布有直接的关系，振幅变小也同样与散射声场分布有关，特别是在高频率3 500 Hz下显得尤为明显.

（3） 在3 500 Hz频率时，随着声学隐身斗篷层数的增加，实际是减小其散射声压幅值，周期性也更加明显，从而导致总声压偏离背景声压的区域变得更小，隐身能力得到增强.

（4） 20层斗篷模型和50层斗篷模型分别在flt;2 500 Hz和flt;3 500 Hz的范围可实现较好的隐身效果，但随着隐身层厚度的增加，其隐身性能都随之降低.为了增加隐身斗篷在高频区间的隐身能力，应增加其隐身层层数，同时选择合适的隐身层厚度.

参考文献（References）

［1］" 毕雪洁，王彪，马林，等.基于双水听器的浅海水声目标深度分类方法［J］.江苏科技大学学报（自然科学版）， 2022， 36（6）：1-8.

［2］" PENDRY J B， SCHURIG D， SMITH D R. Controlling electro-magnetic fields［J］.Science，2006，312（5781）：1780-1782.

［3］" 苏强， 王桂波， 朱鹏飞，等. 国外潜艇声隐身前沿技术发展综述［J］. 舰船科学技术， 2014（1）：9.

［4］" 何佳杰， 江雪， 他得安. 基于声学超材料的超声隐身［C］∥2019年全国声学大会. 深圳：中国声学学会， 2019：25-26.

［5］" 张向东， 陈虹， 王磊，等. 圆柱形分层五模材料声学隐身衣的理论与数值分析［J］.物理学报，201 64（13）：134303.

［6］" ZHAO W ， CHU H ， TAO Z ， et al. Acoustic transmissive cloaking using zero-index materials and metasurfaces［J］. Applied Physics Express， 2019， 12（5）：54004.1-54004.5.

［7］" LIU M ， ZHU W D . Design and analysis of nonlinear-transformation-based broadband cloaking for acoustic wave propagation［J］. Wave Motion， 2019， 92：102421.

［8］" LI P ， YANG F ， WANG P ， et al. A novel design scheme for acoustic cloaking of complex shape based on region partitioning and multi-origin coordinate transformation［J］. Applied Mathematics and Mechanics， 2022， 43（11）：1641-1656.

［9］" POMOT L， PAYAN C， REMILLIEUX M， et al. Acoustic cloaking： Geometric transform， homogenization and a genetic algorithm［J］. Wave Motion， 2020， 92：1-14.

［10］" GE Y， LIU X， HU G. Design of elliptical underwater acoustic cloak with truss-latticed pentamode materials［J］. Theoretical and Applied Mechanics Letters， 2022， 12（4）：221-226.

［11］" XUE Y， ZHANG X. Self-adaptive acoustic cloak enabled by soft mechanical metamaterials［J］. Extreme Mechanics Letters， 2021， 46：101347.

［12］ "GHORESHI M ， BAHRAMI A . Acoustic invisibility cloak based on two-dimensional solid-fluid phononic crystals［J］. Solid State Communications， 2022， 342：114646.

［13］" FAN S W， ZHAO S D， CAO L， et al. Reconfigurable curved metasurface for acoustic cloaking and illusion［J］. Physical Review B， 2020， 101（2）：1-17.

［14］" TORRENT D， DEHESA S J. Acoustic cloaking in two dimensions： A feasible approach［J］. New Journal of Physics， 2008 ，10： 063015.

［15］" 朱锡， 罗忠， 周欣，等. 斜入射下水中隐身夹芯复合材料壳板结构声学设计［J］. 船舶力学， 2009（4）：11.

［16］" 尹可， 马建敏. 声学隐身层结构对隐身性能的影响［J］. 声学技术， 2020， 39（1）：15-21.

（责任编辑：贡洪殿）