重视培养探索性思维 提升数学教学有效性

[摘 要] 探究性思维在提升学生学习主动性、激发学生学习动机、提高教学效率等方面有着重要应用. 在培养探究性思维的过程中，教师应以发展学生为出发点和落脚点，精心设计教学情境，让学生在具体情境的探索中有所发现、有所成长，切实提升学生的知识水平与综合素养.

[关键词] 探究性思维;知识水平;综合素养

探究性思维是高中生应具备的一种思维品质，应在日常教学中进行重点培养. 由于教学时间紧、任务重，因此部分教师重灌输、轻探究，影响学生探究性思维的发展. 要知道，灌输仅能达到浅层次理解，而探究则能彰显问题的本质，有助于学生获得深层次理解. 同时，通过探究还能发现一些新知识、新问题，这对学生创新意识的培养也是极其有益的. 在实际教学中，如何培养学生的探究性思维呢？笔者结合案例简述，欢迎指正.

应用合情推理，培养探究性思维

合情推理是依据一定知识、方法等作出探索性判断的过程，它是探究性思维的一种重要形式. 教师在教学时可以提供一些机会让学生运用观察、猜测、联想等思维形式探索新知，这样既可以加强教学内容的趣味性，又能提升学生的参与性，还能增强学生的探索意识.

例如，研究“空间点、线、面之间的位置关系”的课本内容不难发现，其重点聚集了四个基本事实. 前三个基本事实容易理解，教师可用讲授模式授课. 而对于基本事实4“平行于同一条直线的两条直线平行”，在同一平面内容易理解，但在空间内则不然. 为了让学生“真懂”，教师可以预留时间让学生举例说明，进而主动探索，深化对基本事实4的理解. 在举例说明时，学生多用长方体作为模型，其过程简述如下：

如图1所示，在长方体ABCD-ABCD中，已知AD∥BC，BC∥BC，可以发现AD∥BC. 至此，通过观察与操作，学生轻松地说明在空间内同样存在平行的传递性.

基本事实4的探究以前三个基本事实及平行线的概念为知识基础，引导学生类比平面内平行的传递性，通过观察与推理，说明基本事实4成立. 这样以学生的已有经验为出发点，为学生提供自由探索空间，通过举例直观化抽象定理，促进知识深化和探究性思维形成.

数学学习是发展，非简单继承. 教学目的不仅是让学生“学会”，更重要的是让学生“会学”. 因此，在实际教学中，教师应基于学情，创新教学内容，鼓励学生通过类比、联想等方式探索知识，培养探究性思维. 值得注意的是，合情推理具有主观性，受认知结构、方式、爱好等因素影响，推理结果存在差异. 在教学中，教师应尊重并理解学生的差异，合理利用这些差异，为学生提供创新探索的舞台. 通过有效启发和引导，让学生在观察、探索、联想中有所发现，实现提升.

巧借直观观察，培养探究性思维

学生因数学抽象难学而厌烦，导致课堂沉闷，参与度低. 为打破这一局面，教师可强化直观教学，引导学生观察、探索、感悟，使课堂生动有趣，激发学生学习积极性.

例如，在教学“平面与平面的位置关系”时，教师没有直接给出结果，而是引导学生观察探究，通过亲身经历获得真实感悟，以形成清晰完整的知识认识. 教学前，教师引导学生将两本书平行竖在桌面上，通过操作和观察，学生直观感知两平面平行的位置关系，从而提升学生的空间想象能力. 获得直观感知后，师生共同证明面面平行的判定定理. 这样依托直观感知，可降低思考难度，提高课堂参与度. 完成定理证明后，教师引导学生用图形语言和符号语言进行表征，以此在深化定理理解中，培养学生的数学模型意识，增强学生的转化意识，提高学生的探究能力.

数学知识是抽象的，学生虽能熟记概念和定理，却难以领悟其内涵，影响运用效果. 基于此，教师不妨从一些实例出发，引导学生先观察再操作，这样不仅能帮助学生理解相应知识，还可以提高学生的数学探究能力，提升学生的数学学习信心.

合理创设问题，培养探究性思维

思维源于问题，只有问题才能吸引学生的注意力，激发学生的内在动机. 问题是探究性学习的起点，合理创设问题是培养学生探究性思维的重要手段.

例如，在教学“函数模型及其应用”时，为激发学生的数学学习信心，提升学生的数学思维能力，教师认真研究教学内容，以学生的最近发展区为基础，精心设计问题，引领学生积极探索，培养学生探究性思维. 教师设计问题时应循序渐进，如本节课教学，教师可从学生熟悉的一次函数模型入手，先让学生完成一次函数的练习后再研究指数函数、幂函数等其他复杂函数. 这样由浅入深的探究方式符合学生的认知发展规律，既能帮助学生建立学习自信心，又能激发学生的探究欲，有利于探究性学习的开展.

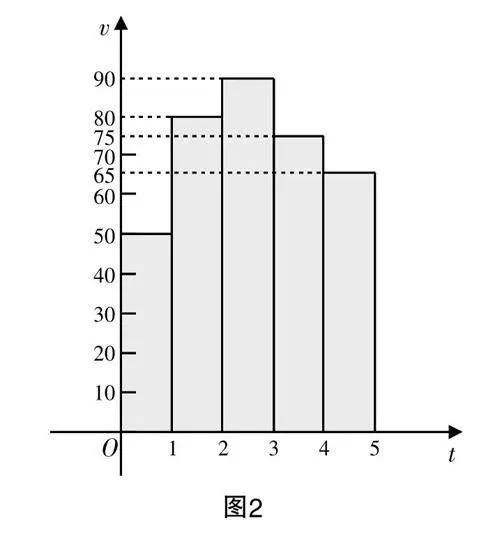
问题1 图2为某辆汽车在某段路程行驶速度v（单位：千米/时）与行驶时间t（单位：时）的关系图.

（1）求阴影部分面积，并说一说它所表示的实际含义;

（2）假设该辆汽车在行驶该路段前里程表的读数为2023（单位：千米），试写出该辆汽车在行驶该路段时里程表的读数S（单位：千米）与时间t（单位：时）的函数解析式，并画出相应的函数图象.

问题2 现有一笔闲置资金欲投资，有三种方案可选.

方案1：每天回报40元;

方案2：第一天回报10元，以后每一天比前一天多10元;

方案3：第一天回报0.4元，以后每一天比前一天翻一番.

你会选哪种方案？

以学生感兴趣的热点话题为切入点，能激发学生思维，促进学生探究性思维的发展，提高学生的数学应用能力.

在教学中，教师要从实际学情出发，合理引入问题，以此撬开学生的数学思维，提高学生的探究能力. 在进行问题引导的探究性学习活动时，问题质量直接关系着教学质量，关系着学生的数学思维发展水平. 因此，在设计问题时，教师一定要把握好难度和梯度，以此通过有效设计来发展学生的探究性思维.

感悟“学以致用”，培养探究性思维

“学以致用”是学习的根本目的，是激发学生学习动机的内驱力. 不过，在应试教育的束缚下，“成绩”成了束缚学生的“枷锁”，许多教学活动都是为了“成绩”开展的，影响学生学习兴趣的激发，限制学生思维能力的发展，不利于学生整体水平的提升. 因此，在教学中，教师要多设计一些实践活动，让学生在“用”的过程中更好地体验数学. 这样不仅可以检测学生知识掌握情况，还能通过具体应用加深学生对知识的理解. 同时，通过实践应用可以提高学生的数学应用水平，提升学生分析和解决问题的能力.

例如，学习完“圆柱的表面积”这一知识后，教师让学生思考一个问题：为什么听装饮料瓶是圆柱形而非方形呢？学生通过思考和计算发现，圆柱形设计集节能、美观、实用于一体，是优质选择.

在教学中，合理引入一些实践性探究活动，不仅可以加深学生对相关知识的理解，还可以激发学生数学研究热情，提升学生的数学应用能力.

其实，培养学生探究性思维有多种方法，教师要灵活调整教学内容，将探究真正融入课堂教学，避免生搬硬套带来枯燥乏味，有效激发学生的数学学习积极性，从而获得最好的教学效果.