基于UbD理论的初中数学章节起始课设计

【摘要】将UbD理论和核心素养有机融入章节起始课，是新课标背景下优化初中数学章节起始课教学、体现单元整体教学观念、落实数学能力培养的新路径。“一元一次方程”是初中阶段方程学习的起始课。在进行课程设计时基于UbD理论，以单元目标为导向，确定合适的评估证据和活动内容，有利于在教学实践中更好地发挥章节起始课的价值，促进学生核心素养的发展。

【关键词】初中数学；章节起始课；UbD理论；“一元一次方程”

作者简介：方慧勤（1983—），女，福建省厦门外国语学校海沧附属学校。

新课标提出，要推进单元整体教学设计，体现数学知识之间的内在逻辑关系，以及学习内容与核心素养表现的关联。章节起始课则是践行单元整体教学观念的有力抓手。如何进行章节起始课设计来引发学生思考、促进学生对数学的理解是需要思考的问题。UbD（全称为“Understanding by Design”，中文翻译为“理解为先的教学设计”）理论把学生的理解放在教学设计及实施的首位，符合新课标的要求［1］。基于此，本文将以初中阶段方程学习起始课“一元一次方程”为例，根据UbD理论，探索通过初中数学章节起始课落实数学核心素养的思路。

一、基于UbD理论的章节起始课的简述

（一）UbD理论简述

UbD的基本思想是“逆向”和“理解”，核心特征是“逆向教学设计”，即先确定单元目标和评价标准，再据此设计活动。教师在教学过程中应始终关注两点：其一，如何用表现来说明学生已经掌握了学习内容；其二，如何用证据来说明目标已经达到预期。在“为理解而教”时，教师要认识到自己是学生培养用表现展示理解的能力的指导者，而不是将自己的理解告知学生的讲述者［2］。这一观点会影响初中数学章节起始课的设计。

（二）章节起始课简述

1.概念的界定

从时间的角度来看，章节起始课是指某章的首节课；从课程安排的角度来看，章节起始课有利于让学生深刻了解某章的相关问题、核心思想、基础内容框架，且注重其与现有课程体系的关联性；从结果的角度来看，章节起始课能指引学生把握学习方向，明确学习目标。章节起始课可以分成三类：领域（大单元）起始课、领域沿途起始课、领域终端起始课［3］。

2.章节起始课教学存在的问题

笔者所在的学校以“立足单元教学，聚焦章节起始课”为主题开展了校本研修活动。笔者在听课过程中，发现本校教师在章节起始课教学中存在缺乏单元整体教学观念、忽视课堂评价的问题。章节起始课旨在指导学生形成学习和研究某章内容的思路和方法。同时，“教—学—评”一致性是教学的起点，也是教学的终点。有效的章节起始课应重在建立新旧知识关联、构建知识整体框架、渗透思想方法，这样才能让教师在教学中做到有的放矢。

（三）基于UbD理论的章节起始课设计流程

章节起始课设计要关注学生已有的认知基础和学生今后的学习方向，遵循UbD理论进行逆向教学设计。在确定预期结果阶段，教师要合理安排学生学习内容的先后顺序。在规划教学活动阶段，教师要抓住以下几个关键点：学生参与学习并达到预期效果所需要的知识和能力有哪些？如何让学生更有效地习得知识和能力？用什么教学方式来开展教学活动？为达成教学目标需要哪些教学资源和材料？

二、基于UbD理论的章节起始课案例

为了帮助其他教师更好地将UbD理论应用于教学活动中，笔者选用的例子是人教版七年级上册教材关于“一元一次方程”的内容。本课是学生后续学习二元一次方程组、分式方程、一元二次方程的基础。衔接知识、迁移方法、指引方向是本课的目标。

（一）“一元一次方程”教学分析

课标分析：“一元一次方程”是义务教育数学课程第四学段数与代数的重要内容。新课标要求学生能针对具体问题列出方程，理解方程解的意义，经历估计方程解的过程，掌握等式的基本性质，能解一元一次方程。

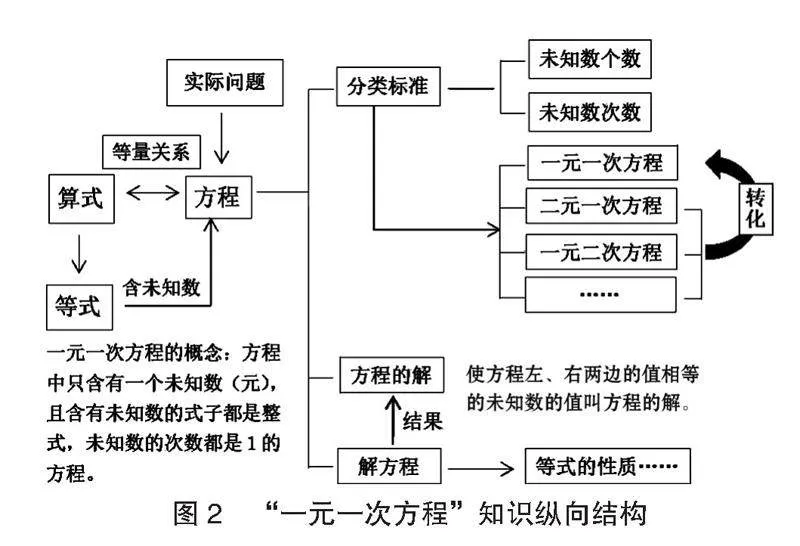
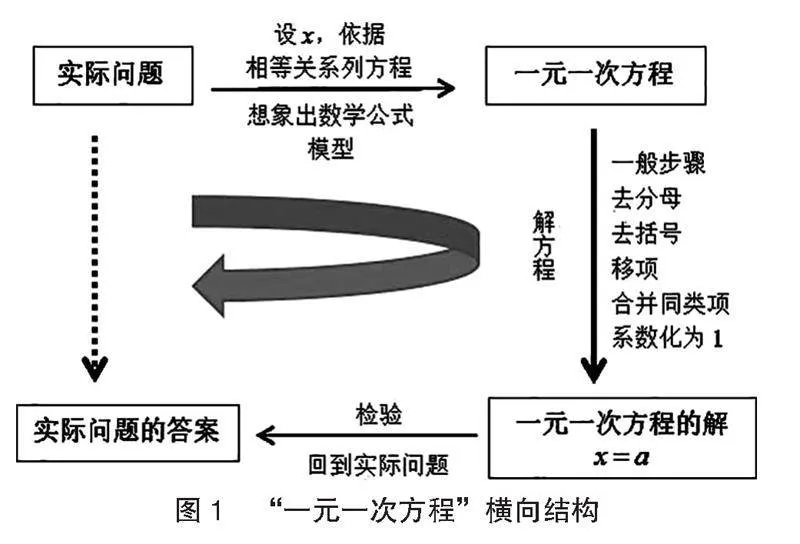
教材分析：关于本课的教材内容的横向结构如图1所示、所涉及知识的纵向结构如图2所示。对于章节起始课，教师应重视章节目标的一致性、章节知识的完整性，自始至终地把“学生自我认知”放在首位。

学情分析：初中学生记忆力相对较强，对于情境的记忆一般比较深刻；逻辑思维有一定的发展，但仍需具象思维做支撑；学习兴趣易受学习难度影响，易产生畏难情绪；不太善于自我评价，易被他人的评价左右。初中学生在小学阶段已经学过简易方程，具备一定的运算能力和生活经验，初步形成方程思想和模型观念。但是有的学生对“从算式到方程”的内容存在困惑，对一元一次方程概念的认识不清晰，对概念学习的一般路径“从实际问题中抽象出模型—概括模型的本质属性—下定义—探究解法—解决实际问题”的运用缺乏经验。这些问题都需要在本课教学中得到解决。

（二）“一元一次方程”章节起始课设计

1.教学框架

基于UbD理论，笔者运用逆向教学设计思维为本课构建的教学框架如表1所示。

2.教学过程

（1）情境引入，提出问题，初显主体框架

情境：2023年10月1日早晨，客车司机黄师傅与卡车司机李师傅同时从厦门天湖城小区出发按相同的路线行驶至武夷山。卡车的时速为60 km/h，客车的时速为70 km/h，卡车比客车晚1小时经过武夷山三木加油站。请你用学过的知识计算天湖城小区到武夷山三木加油站的路程，说出其中的道理，并思考列算式或方程来解决问题的具体步骤是怎样的。

笔者以国庆小长假为背景创设贴近学生真实生活的情境，进行问题设计，旨在引导学生解决实际问题，让学生体会解法的多样性，引出本课的主体框架，为后续研究做铺垫。

（2）集思广益，解决问题，传授思考方法

UbD理论强调，理解可以被看作是探究和反思活动的预期结果。笔者在课堂中发现，有些学生对于所列的式子一知半解。对此，笔者用列表法搭建数与式之间的桥梁，帮助学生厘清题目中的时间与路程的关系［4］。

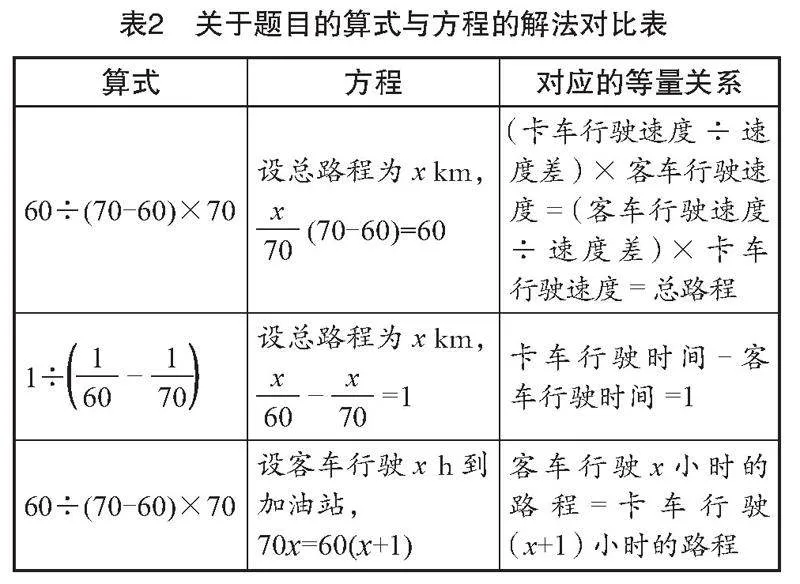
由于通过解读关于时间与路程的数据得到的等量关系需要逆推，部分学生理解起来有困难，因此笔者引导学生将未知量通过用字母表示的方式转化为已知量。同时，笔者基于学生的认知特点，展示算式与方程的解法对比表（如表2所示），助力学生建立方程与算式的联系，初步认识列方程来解决问题的一般步骤—“罗列已知量、未知量—找等量关系—设未知数—列方程—解方程”。

方程作为一种重要的数学模型，贯穿于初中数学课程的始终。新课标强调，在数与代数的教学过程中，要关注数学知识与实际的结合，让学生在实际背景中理解数量关系和变化规律，经历从实际问题中建立数学模型、求解模型、验证反思的过程，形成模型观念。这说明方程相关内容的章节起始课教学应基于数学的整体性，突出建立模型、求解模型的过程，发展学生的模型观念。

三、基于UbD理论的章节起始课的思考

其一，章节起始课需要贯通知识线、思想方法线。教师在教学中既要关注本课的教学内容，又要注重对整个章节教学意图的渗透。这有利于教师在备课时充分考虑到不同层次学生的理解程度，有针对性地做好分层设计的准备，从而促进全体学生的发展。

其二，新课标理念下的课堂质量主要取决于学生的表现。为了引导学生获得学习方法，教师在教学过程中要根据评估预期结果所需的证据，对课堂活动（包括教学方法和资源、材料的选择，课堂问题链的设计等等）做进一步的优化。对于章节起始课，教师应该重点思考如何设计才能让思想方法的渗透水到渠成。

其三，章节起始课的知识线、思想方法线都指向学生的后续学习。比如，通过“一元一次方程”这节课，学生不只是多习得了一种解决问题的方法，更重要的是将解决问题的范围从已知数拓展到未知数，学会了自主探究新知识，数学核心素养也得到了发展［5］。

【参考文献】

［1］ 何俊杰，孟志鑫.基于UbD理论的初中数学单元整体教学设计：以人教版“一元二次方程”为例［J］.中小学课堂教学研究，2023（10）：53-58.

［2］ 威金斯，麦克泰格.追求理解的教学设计：第2版［M］.闫寒冰，宋雪莲，赖平，译.上海：华东师范大学出版社，2017.

［3］ 邢成云，王尚志.初中数学“章起始课”的探索与思考［J］.课程·教材·教法，2021，41（3）：76-82.

［4］ 朱小平.基于“理解”的教学实践及思考：以“从算式到方程”为例［J］.中学数学教学参考，2021（26）：66-69.

［5］ 李会芳.核心素养视域下基于APOS理论的高等数学概念教学探究［J］.教育观察，2024，13（13）：62-65.