突出本质 深度自主 发展素养

单元教学课的开展目的不仅是为学生解决本节课的“眼前问题”，更重要的是通过数学知识的整体建构和经验方法的总结，引导学生准确把握知识的实质内涵和生成路径，渗透数学基本思想方法和关键能力的培养，实现教育价值。近期再次观看全国教书育人楷模李庾南老师展示的“怎样研究几何图形——以平行四边形为例”的示范课，感受颇多。李老师以学习几何图形为主题，以平行四边形为例，基于对数学本质的深刻理解，与学生深度对话，在探索平行四边形的定义、性质、判定等知识关联中发展学生素养。笔者认为这不仅体现了教育名家对“掌握基本方法，熟悉基本套路”教学的追求，更体现了教育名家对教学知识系统的深刻理解。笔者现整理三个教学片段，分享个人反思，以期对一线教师，尤其是对青年教师有所启发。

一、教学片段

片段1：回顾定义，获得研究对象

师：同学们，今天我们一起来研究怎样学习几何图形。对于一个新的几何图形，我们首先要把它的基本特征用数学语言表达出来，这种表达就称为图形的定义，然后要分析定义的条件有几个要素。现在以平行四边形为例进行研究。

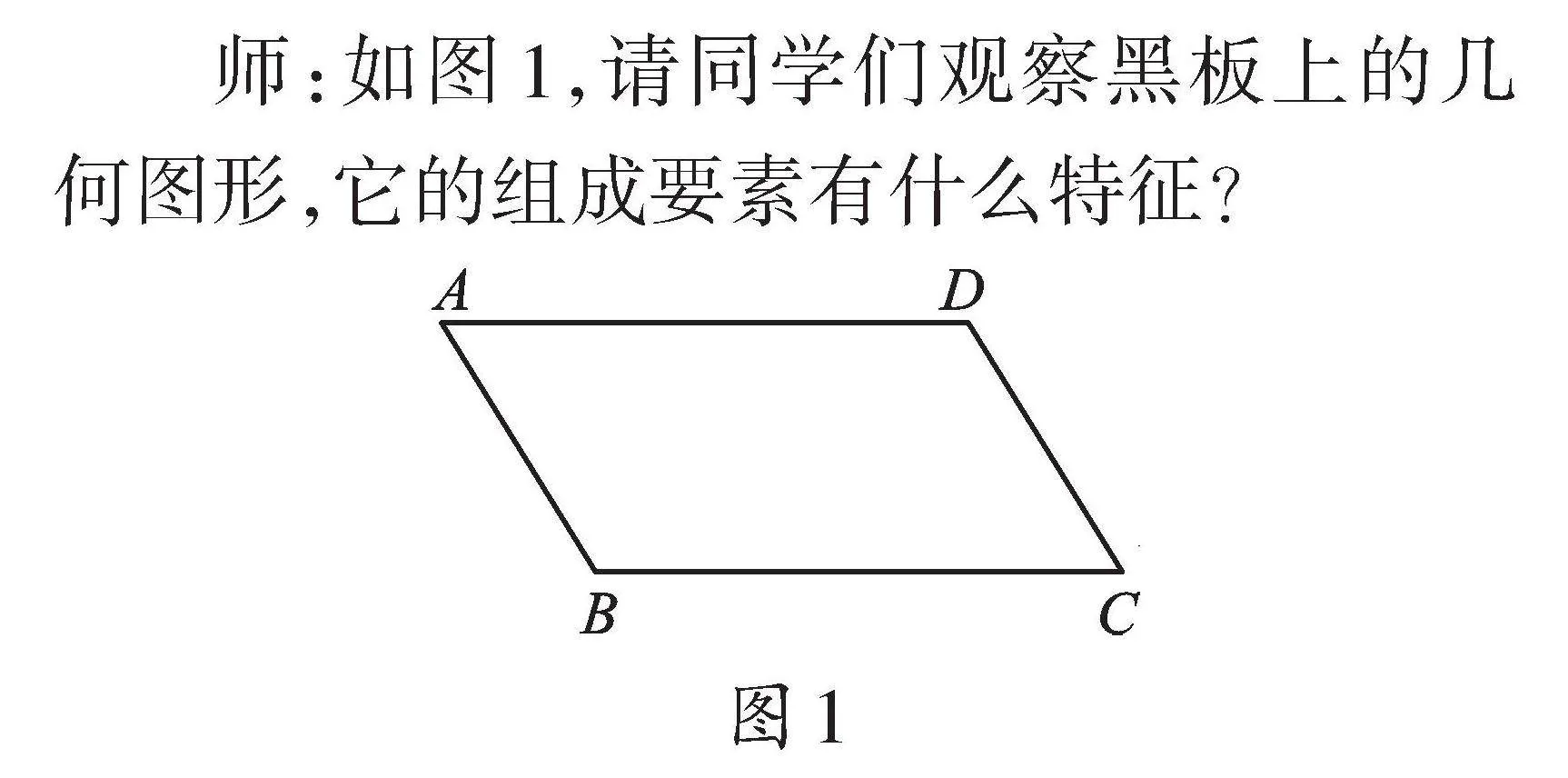
师：如图1，请同学们观察黑板上的几何图形，它的组成要素有什么特征？

生：它是四边形，而且有两组对边分别平行。

师：那么用数学语言如何来表达它的这种特征呢？

生：有两组对边分别平行的四边形就是平行四边形。

师：这个命题的条件是什么？

生：条件是一个四边形的两组对边分别平行。

师：是的。条件有两个，第一是四边形，第二是两组对边分别平行。这个定义还可以用符号语言来表达，如图1，在四边形ABCD中，因为AB∥CD，AD∥BC，结论：这个四边形是平行四边形。

片段2：关联联想，探究研究对象

师：如果告诉你这个几何图形是平行四边形，你能说出对边的位置关系吗？

生：两组对边分别平行。

师：所以在研究几何图形的时候要知道定义的双重作用：定义中的条件不仅是这个图形判定的原始方法，也是这个图形所具有的基本性质。那就先从基本性质出发，由两组对边分别平行能推导出什么关系？

生：数量关系。

师：数量关系通常研究的是线段和角。我们运用平行的性质“两直线平行，同旁内角互补”，能得到什么结论？

生：因为AB∥CD，所以∠B+∠C=180°，因为AD∥BC，所以∠C+∠D=180°，所以∠B=∠D，理由：同角的补角相等。同理，∠A=∠C。

师：由此我们得出平行四边形的两组对角分别相等。

师：另外，两直线平行，内错角相等。要形成内错角，就要有截线，如何构造这条截线？

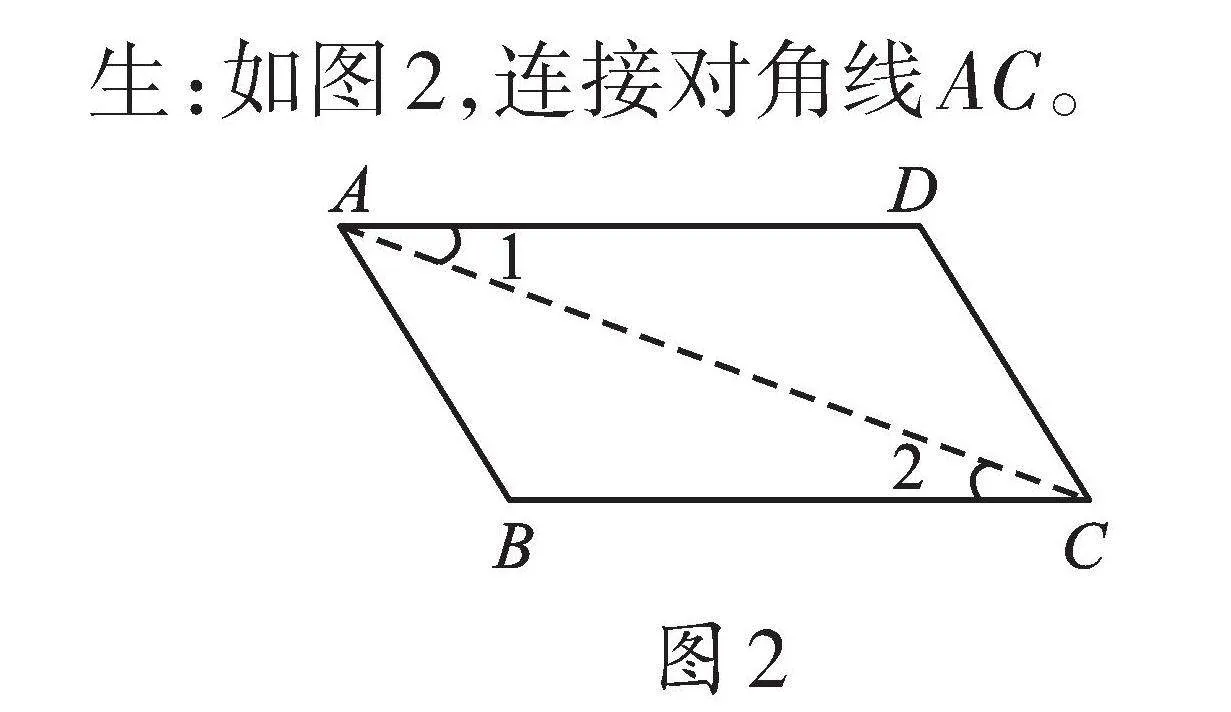
生：如图2，连接对角线AC。

师：由AD∥BC，推出∠1=∠2。由AB∥CD，推出∠BAC=∠ACD，对角线将平行四边形分成了两个全等三角形，此时可以推导出组成平行四边形有关要素的数量关系吗？

生：两组对边分别相等。

师：同学们，平行四边形的两组对边分别平行对两条对角线的数量关系与位置关系有没有影响呢？从数量关系来看，平行四边形的两条对角线相等吗？

生：不相等。

师：为什么不相等？

生：连接BD，想要证明BD=AC，如图3，就要证明△ABC和△DCB全等，条件已经有AB=CD和BC=CB，还要有一个夹角相等，即∠ABC=∠BCD=90°，但条件中并没有告诉我们这两个角是90°，因此不能推导出对角线相等。

师：接着我们来思考平行四边形的两条对角线的位置关系，请同学们以小组为单位讨论交流。

生：我们发现对角线AC和BD相互平分。

师：你们怎么知道的？

生：由平行四边形两组对边分别平行且相等，得到AB=CD，AB∥CD，AD∥BC，进而得到∠1=∠2，∠ABO=∠CDO，可以证得△ABO≌△CDO，即AO=CO，BO=DO。

师：是的，平行四边形两条对角线的相交是特殊相交——互相平分。这样我们就得到平行四边形的三个性质命题。这三个性质命题的条件只有一个：四边形是平行四边形。结论是：两组对边分别平行且相等、两组对角分别相等、两条对角线互相平分。

片段3：逆向思考，升华研究对象

师：刚才所得到的性质定理都是由两组对边分别平行作为基础，所以平行四边形的定义是一棵大树，三条性质是长出来的枝。研究平行四边形的判定也要类比这样的方法。根据定义，我们就要研究一个四边形需要具备什么样的条件才能够得到两组对边平行。联想平行线的判定：“同旁内角互补，两直线平行”，此时这个四边形要具备什么条件？

生：两组对角相等，再加上四边形内角和为360°，就可以利用“同旁内角互补，两直线平行”来证明两组对边平行。

生：根据研究性质的经验，构造截线，连接对角线AC，如图2，要证明∠1=∠2和∠BAC=∠ACD，只需要证明△ABC≌△CDA即可，此时还少条件：第一，如果有AD=BC，再加上AD∥BC就可以了；第二，如果用“SSS”来证明这两个三角形全等，那么这个四边形要满足两组对边分别相等。另外，如果对角线互相平分，由全等三角形依然可以得到角相等，进而得到两组对边分别平行。

师：将上述的几种思路经过严格证明后就能得到平行四边形的判定定理。显然，判定定理的条件、结论与性质定理是相反的，所以它们是互逆命题。

二、感悟反思

1.突出学科本质，深度自主建构

何为本质呢？就是一类事物区别于其他事物的标志。平行四边形区别于其他图形的标志就是“有两组对边平行的四边形”，这是其他几何图形所不具有的。反之，具备这样的条件，这个几何图形就是平行四边形。所以性质和判定就应该从定义中生长出来，就像植物一样，定义是根，其余枝干上的研究都是从这个点上长出来的，从这个角度上来讲，性质与判定的学习顺序其实无本质的区别，它们应该是融为一体的，我中有你，你中有我。定义、性质、判定的教学，其本质应反映数学几何图形的内涵，即边、角、线的位置关系和数量关系。性质和判定的学习要一致，这是数学学习该有的逻辑体系。本节课从边的相等以及边的平行角度来研究平行四边形，通过探究从特殊到一般的关系，追求逻辑连贯和前后一致的几何教学，在经历一类图形的整体研究过程中，关注思想方法在知识建构中的自然渗透。本节课的上位逻辑是平行线的性质及判定，李老师相机引导，深度对话，凸显知识之间的关联。

章建跃教授曾说过，理解数学是教好数学的前提。李老师正是站在已经理解数学的高度，抓住数学抽象的特点，关注学生数学思维的发展对学生终身发展的影响来设计教学。我们看到，教育名家从学科内部的联系来重构教学内容，用教材教，而不是教教材，一气呵成，把这些知识之间的内在逻辑联系在整体视角下理清楚，自主建构出新的知识框架，为学生今后学习几何图形明确路径，进而促使学生获得良好的学习经验。

2.突出教学本质，深度自主发展

《义务教育数学课程标准（2022年版）》指出，数学教学应该注重数学知识之间的联系，潜移默化地让学生感受知识之间的联系。欧式几何就是以最基本的定义为地基形成的一座大厦，片段教学中，李老师从观察图形边的关系出发，从中找到教学的逻辑起点——定义，分析定义的双重作用，从定义出发合理猜想，再进行推理论证。

同时，教是为了不教。教学本质上是师生双方互动的过程，在这个过程中，教师需要给学生提供指导性的意见，而不是把原生态的问题抛出来消耗学生宝贵的课堂时间。今天虽然以平行四边形为例，但是它的研究方法是研究几何图形的一般方法。如果平行四边形的边和角有了特殊的关系，平行四边形的图形、性质和判定又会有什么样的变化？所以教学片段传达给我们的是对教学本质的理解，即教学过程中的元认知策略，利用类比学习的方法来积累研究平面几何的套路和思维，从特殊入手，发现共性，抽象概括，从而形成一般结论。经历了研究平行四边形的过程之后，学生不仅获得了新知识，还获得了研究策略和方法，激发了深入探究的热情和自信。

通过对李老师这节课的课例设计、教学艺术等分析，笔者获得的是对自身专业成长的再教育，即从默会知识，到“悠然神会，妙处与君说”的显性传递。学生对知识的学习与探索，在于积累解题经验，提升解题能力，感悟知识中蕴含的数学思想方法。李老师对数学教学进行高深理解与研究后，再对学生的学情做出正确的评估，建构出学习几何图形的通性通法，创设具有概括性、系统性、有梯度的教学环节，引导学生独立思考、主动探索、合作交流，落实学生的主体地位，凸显教师的主导作用。学生不仅体会到数学知识内在的逻辑关系和巧妙的研究方法，而且提升了思维境界，为自主发展搭建了更广阔的平台。

总之，从学科逻辑到学习逻辑是教师必须学会思考的问题。我们看到教育名家充分关注内容的结构化整合，突出数学知识的本质，使得学生在掌握知识技能的同时，感悟数学知识的本质，学会“数学地思考”，形成和发展核心素养。正如李老师的这一节生动的数学课，通过单元教学的思想引领，学生掌握了研究一类图形及其关系的基本方法，这是对数学知识本身及其发生、发展过程中反映的数学思想和方法的再概括和再组织，也正是李老师找准核心素养落地发展的一种有效的教学设计与实践，集中体现了教育名家的智慧和创新精神。

（作者单位：江苏省宿迁市中小学教学研究室）