基于熵权和自适应负载编码的配电网故障恢复算法研究

摘要：针对传统故障恢复方案评价方法难以制定合理目标权重的问题，文章提出了一种基于熵权的综合权重确定方法，对故障恢复方案的优劣进行评价。针对传统群体智能算法难以应对负载无法完全恢复的问题，文章提出了一种自适应负载编码的方法融入群体智能算法，将不满足约束条件的个体做负载切除处理，使得智能算法中的每个编码为电气角度的可行解，通过算法的逐步迭代得出使得目标函数最优的解。经算例验证该算法可以得到全局最优解并且可以解决大面积负载恢复问题，具有一定的工程价值。

关键词：故障恢复；配电网；群体智能算法；熵权；自适应负载编码

中图分类号：TM727 文献标志码：A

0 引言

故障恢复可以有效降低因故障导致的停电损失，是保障配电网的安全、稳定运行的重要技术手段。

配电网故障恢复属于非线性的整数组合优化问题［1-3］，须综合考虑负载恢复量、设备容量、电能质量、配电网拓扑运行约束、电压和电流约束等因素，从而得出最优的供电恢复方案。近年来，群体智能算法因优良的全局寻优性能得到了国内外众多研究学者的广泛关注并获得了迅速的发展。群体智能算法的核心思想是对故障隔离后的配电网进行网络重构。为了确保配电网的辐射状运行约束，粒子群算法［4-6］、遗传算法［7-9］和蚁群算法［9-10］等分别基于各自算法特点提出了将不可行解修正为可行解或避免产生不可行解的编码方法，在很大程度上提升了群体智能算法的计算效率。然而，当所需恢复的负载大于配电网的供电能力时，则须要切除部分负载，否则无法得出满足约束条件的故障恢复方案。但是，现有文献均未讨论处理供电能力不足时供电恢复的编码方法，影响了群体智能算法的应用推广。故障恢复方案的评价方法对于群体智能算法最优方案的制定具有重要作用。孙雅明等［11］建立的隶属度函数具有一定程度的主观性，难以准确建立。黄弦超等［12-13］采用支配原则对恢复方案进行等级划分，存在同一等级对应多个方案的情况，同时该方法没有涉及目标函数的不同重要程度。

针对上述问题，本文采用基于熵权的综合权重对故障恢复方案的优劣进行评价，在现有群体智能算法的基础上采用自适应负载编码策略来解决供电能力604114a7c3621689db0452caa82f22c3a1d4f2558abb0aa6b5cd8005cd4dd9fe不足的问题。

1 目标函数及约束条件

1.1 目标函数

配电网故障恢复的目标函数如下：

（1）未恢复负载量。

minf1=∑i∈APi（1）

式中，A为未能恢复供电的负载节点集合；Pi为负载节点i的负载量。

（2）开关操作量。

minf2=∑i∈T|Ki-K′i|（2）

式中，T代表所有开关的集合；Ki′、Ki代表供电恢复前后的开关状态。其中，开关状态由1和0分别表示开关处于闭合和断开状态。

（3）网络损耗。

minf3=∑i∈BPiloss（3）

式中，B为所有支路的集合；Piloss为支路i的有功功率损耗。

（4）载荷平衡。

minf4=maxi∈PLiLNi－mini∈PLiLNi（4）

式中，P为所有支路集合；Li为支路i的负载容量；LNi为支路i的额定容量。

（5）电压质量。

maxf5=mini∈N（Vi）（5）

式中，N为所有节点集合；Vi为节点i的电压。

1.2 约束条件

配电网故障恢复须要满足的约束条件如下：（1）配电网的拓扑约束；（2）配电网的电压约束；（3）配电网的电流约束。

2 基于熵权的评价方法

2.1 熵权

熵权是一种依据各个方案及其目标函数值所包含的信息来确定权重的客观赋权法［14-15］，是评价多目标问题比较理想的尺度。故障恢复的各个目标函数值具有不同的量纲，为了方便比较须要对目标函数值进行标准化处理。本文采用姚玉海等［4］所述方法进行标准化，在此不做赘述。其中，未恢复负载量、开关操作量、网络损耗和载荷平衡均属于成本型指标，电压质量属于效益型指标。

假设有m个待评价方案，每个方案对应n个目标函数值，标准化后的判断矩阵R为m行n列。

熵的定义如下：

Hj=-（∑mi=1fijlnfij）/lnm（6）

fij=rij/（∑mi=1rij）（7）

式中，Hj为目标函数j的熵值；rij表示第i个方案第j个目标函数标准化后的值，rij∈［0，1］，i=1，2，…，m，j=1，2，…，n。

在标准化后，判断矩阵R部分元素为0，导致fij=0。为了使lnfij有意义，在不违背熵的含义下，将fij修正如下：

fij=（1+rij）/（∑mi=1（1+rij））（8）

定义第j个目标函数的熵权为：

wj=（1-Hj）/（n-∑nj=1Hj）（9）

式中，wj为目标函数j的熵权值。

熵权值wj∈［0，1］，且满足下式：

∑nj=1wj=1（10）

由熵权的定义可知以下特点：

（1）各个被评价方案在目标函数j上的值相同时，熵权值为0。即该目标函数没有向决策者提供有用信息，该目标函数的影响被剔除。

（2）当各个方案在某目标函数值上具有较大差异时，对应的熵权值会比较大，表明决策者应重点考虑该目标所提供的信息。

（3）目标函数的熵值与熵权值成反比，熵权值与目标函数重要性成正比。

（4）熵权并不代表目标函数的实际重要程度，而是反映了目标函数有用信息量的多寡程度。

熵权是一种客观权重［16］，是根据客观存在的各个方案及其目标函数值得出的。熵权值依赖于客观数据，导致有时得出的权重值与人们的认识存在一定差距。同时，为了避免专家经验对各个目标函数赋权的主观性影响，本文将专家权重和熵权进行合理结合从而得到综合权重。

目标函数j应用专家经验法的权重值为λ并且满足下式：

∑nj=1λj=1（11）

综合权重的定义方法如下：

aj=wjλj∑nj=1wjλj（12）

式中，aj为目标函数j的综合权重值。

2.2 恢复方案的评价

群体智能算法实质上是通过种群中的优秀个体（个体即对应故障恢复的方案）来不断“引导”种群向最优解的邻域逼近，通过多次迭代后最终得到最优解。因此，通过评价得出群体中的优秀个体对获得最优解至关重要。

群体智能算法在迭代过程会对种群进行更新，相应的“参照物”也随之发生变化。基于熵权的评价方法会导致同样的故障恢复方案在不同的种群中适应度不同。虽然相同的方案在不同迭代次数中的适应度会发生变化，但优秀的方案仍然拥有较好的适应度，在不断的迭代过程中逐渐占优，并不影响最优解的得出。

群体智能算法基于熵权法评价的更新步骤如下：

（1）根据故障恢复问题的目标函数，采用专家经验法确定各个目标函数的主观权重。

（2）将当前种群中的每个方案对应的各个目标函数值分别求出，再对其进行标准化处理，得到判断矩阵R。

（3）根据所述熵权法计算得出熵权值，再结合专家经验法的权重计算得出综合权重值。

（4）采用式（13）计算出种群中所有个体的适应度，适应度最大为本次迭代的最优解。

fi=∑nj=1aj×Rij（13）

式中，fi为adee57371af14c3e25f939dea45d894f方案i的适应度。

3 自适应负载编码

群体智能算法的个体编码方法主要是为了处理配电网的拓扑约束问题，技术已经非常成熟。群体智能算法在处理不等式约束（即电流、电压约束）时，通常以惩罚项的方式引入适应度，将违反不等式约束个体的适应度通过惩罚变为最差个体，进而在逐次迭代过程中将该类个体淘汰。然而，当所需恢复的负载大于配电网的供电能力时，这种编码方法就无法获得满足不等式约束的方案。因此，为了得出满足约束条件的故障恢复方案，须在现有编码技术的基础上叠加自适应负载切除的编码方法。

故障恢复方案不仅要保证未恢复负载量尽量小，还要优先保障配电网中重要负载的供电。因此，在负载切除过程中，应优先切除重要程度低的负载，同时可保证约束条件的最小负载。

对不满足电流或电压约束的个体采用负载切除的方式使其满足不等式约束，从而使得群体中的每个个体均为电气角度的可行解。违反电流约束条件的情况属于电网安全问题，违反电压约束条件的情况属于电能质量问题。当同时违反电流约束和电压约束时，应优先处理安全问题，即先通过负载切除保证电流约束条件，之后再处理电压约束问题。为了满足配电网的拓扑约束，应从电网末端向电源端的方向逐步切除负载。

自适应负载编码步骤如下：

（1）对负载进行重要等级划分，负载等级越低重要性越高。

（2）采用现有群体智能算法的编码方法生成个体。

（3）对个体对应的配电网拓扑结构开展潮流计算。

（4）根据潮流计算结果判断该个体是否存在违反电压或电流约束的情况。若不存在则不需要负载切除，编码结束。若存在不满足电流约束条件则转步骤（5），若仅存在不满足电压约束条件则转步骤（7）。

（5）以电源侧为起点，采用广度优先遍历顺序将电网中不满足电流约束条件的支路矩阵列出。取出该支路矩阵最后一条支路（为便于描述假设为支路i）并计算出支路i的越限量，即实际负载量减去额定负载量的值。然后将支路i下游末端负载重要程度最低且负载量最小的节点依次切除，直至切除的负载量大于支路i的越限量。

（6）对完成负载切除的个体所对应的配电网拓扑结构开展潮流计算并转步骤（4）。

（7）以电源侧为起点，采用广度优先遍历顺序将电网中不满足电压约束条件的节点矩阵列出。取出该节点矩阵最后一个节点（为便于描述假设为节点i），将节点i下游末端负载重要程度最低且负载量最小的节点切除，负载切除后转步骤（6）。

群体智能算法在群体更新迭代过程中具有一定程度的随机性，这会不可避免地产生一些质量较差的个体，即这些个体对应违反电流或电压约束的拓扑结构。随着算法的进行，这些差的个体虽然会在迭代过程中被自然淘汰，但仍然占据了一定的计算资源。因此，可以在算法迭代一定次数后判断是否存在满足电压或电流约束的个体，如果不存在，再投入自适应负载编码，可以降低对计算效率的影响。

4 故障恢复算法

基于熵权和自适应负载编码的配电网故障恢复算法步骤如下：

（1）输入电气基本信息和算法参数，设置算法结束次数T并令k=1。

（2）初始化种群并计算种群中每个个体的适应度。

（3）当k≤T/3时，更新种群，即采用种群智能算法设定的交叉、变异以及算法自身的策略产生新一代种群。计算种群中每个个体的适应度并令k=k+1。

（4）当k＞T/3时，更新种群并判断种群中是否存在不违反电压和电流约束条件的个体。如果存在则不须要投入自适应负载编码，如果不存在则投入自适应负载编码。计算种群中每个个体的适应度并令k=k+1。

（5）判断k=T是否成立，如果成立则输出当前最优个体为恢复方案，反之则转步骤（3）。

5 算例分析

本文采用图1所示的69节点配电网为例对本文方法进行验证。该电网共含有69个节点和73条支路，假设73条支路均装设具有三遥功能的开关设备，图中实线和虚线表示开关处于闭合和断开状态。该配电网相关参数参见文献［17］。

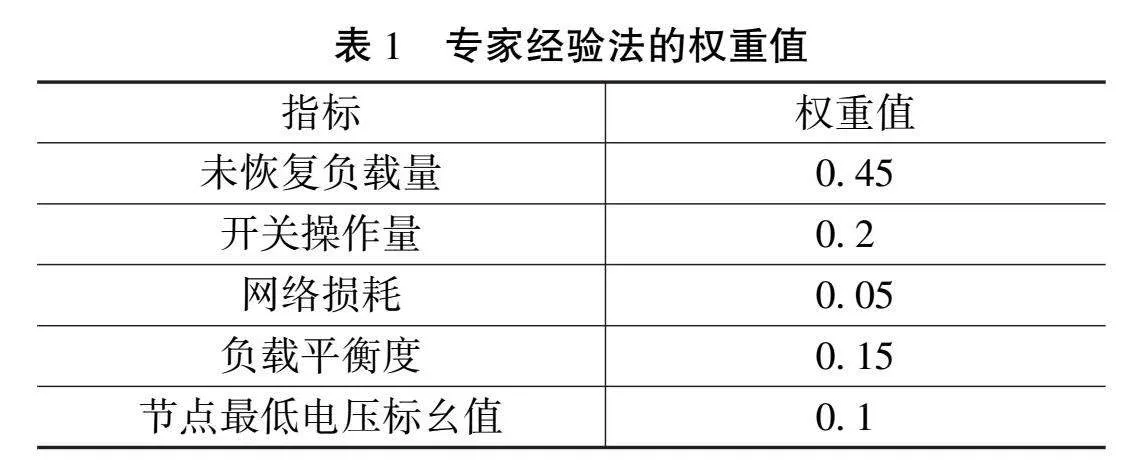
本文采用粒子群算法［6］结合本文方法基础结合求解配电网故障恢复问题。目标函数对应的专家经验法权重值如表1所示。

算例1：（4，5）故障并退出运行，假设全网负载具有相同重要等级。

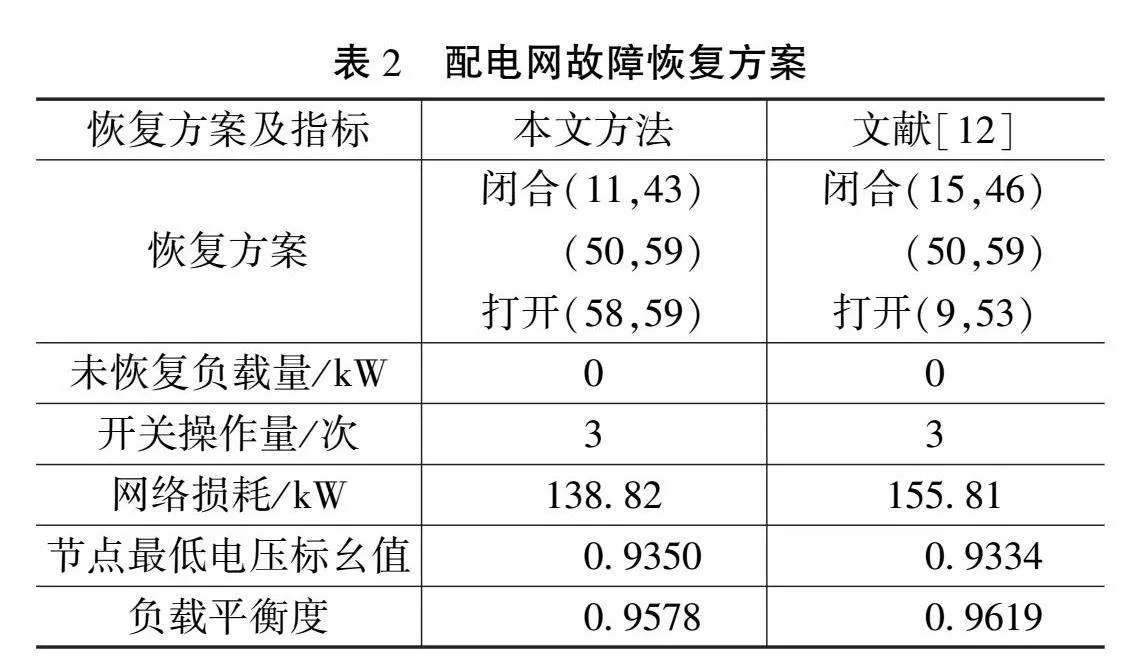
表2列出了本文方法和文献［12］针对算例1计算得出的恢复方案及其目标函数值。其中，对比文献中的各个目标函数值是依据该文献所列恢复方案计算得出的。从表2可知，本文方法所得恢复方案在网络损耗、节点最低标幺值和负载平衡度方面具有更好的结果。该算例说明了本文方法的优越性。

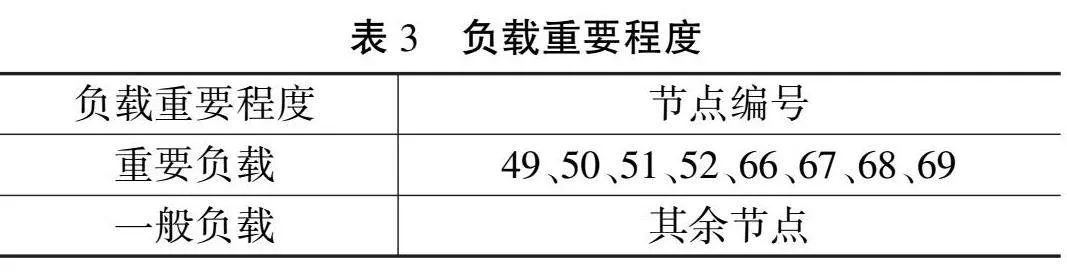
算例2：（3，4）故障并退出运行。电网负载重要等级如表3所示。

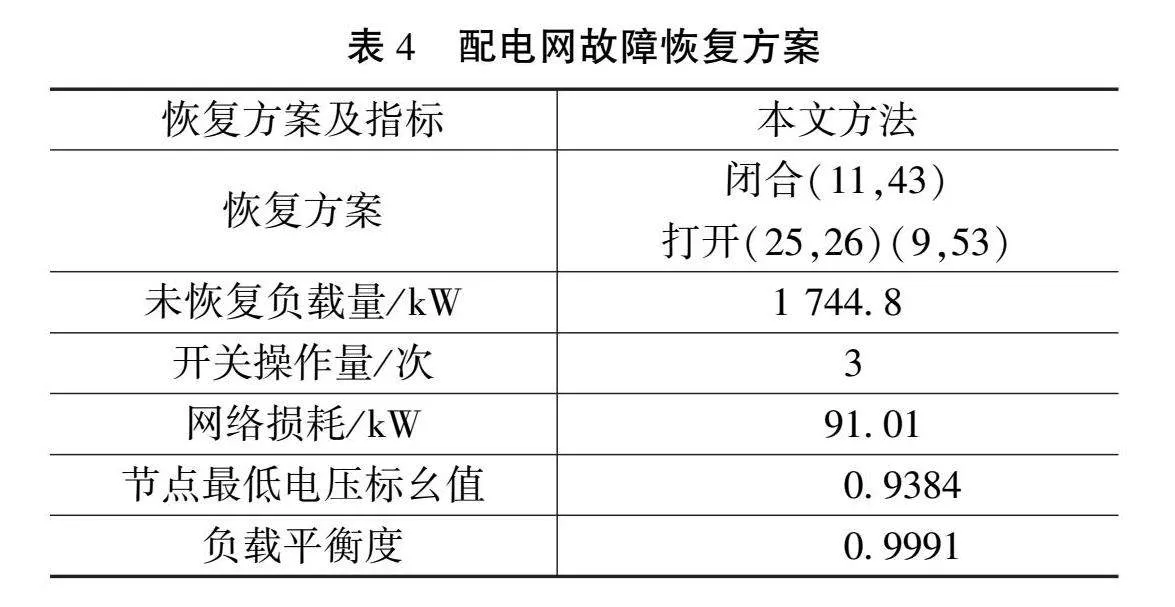
表4列出了针对算例1计算得出的恢复方案及其目标函数值。由于算例2的失电范围较大，电网的供电能力不足以恢复所有停电负载。算法投入了自适应负载编码并得出了满足约束条件的最优故障恢复方案，说明了本文方法的有效性。从表4可以看出，恢复方案保障了所有重要负载的供电。

6 结语

本文将基于熵权的综合权重和自适应负载编码融入群体智能算法，可以得出以下结论。

熵权是反映种群中不同个体同一目标的信息，即种群的纵向信息。专家权重考虑到目标和目标之间的相对重要程度，即横向信息。通过熵权和专家权重相结合的综合权重对指标进行评价可以更好地寻找出种群中的优秀解，使得算法可以更好地求得全局最优解。

本文在传统群体智能算法编码技术的基础上提出了自适应负载编码方法。该方法可以对种群中不满足电压、电流约束条件的个体进行负载切除，使得种群中的个体不仅满足配电网拓扑约束，还同时满足电压、电流约束条件。自适应负载编码可以有效解决群体智能算法在求解故障恢复问题时供电能力不足的情况，增强了群体智能算法的适用性。

参考文献

［1］许寅，和敬涵，王颖，等.韧性背景下的配网故障恢复研究综述及展望［J］．电工技术学报，2019（16）：3416-3429.

［2］HAFEZ A A，OMRAN W A，HIGAZI Y G.A decentralized technique for autonomous service restoration active radial distribution networks［J］.IEEE Transactions on Smart Grid，2018（3）：1911-1919.

［3］SCHNEIDER K P，TUFFNER F K，ELIZONDO M A，et al.Enabling resiliency operations across multiple microgrids with grid friendly appliance controllers［J］.IEEE Transactions on Smart Grid，2017（5）：4755-4764.

［4］姚玉海，王增平，郭昆亚，等.基于E占优的多目标二进制粒子群算法求解配电网故障恢复［J］.电力系统保护与控制，2014（23）：76-81.

［5］李振坤，陈星莺，余昆，等.配电网重构的混合粒子群算法［J］.中国电机工程学报，2008（31）：35-41.

［6］卢志刚，杨国良，张晓辉，等.改进二进制粒子群优化算法在配电网络重构中的应用［J］.电力系统保护与控制，2009（7）：30-34.

［7］毕鹏翔，刘健，刘春新，等．配电网络重构的改进遗传算法［J］．电力系统自动化，2002（2）：57-61.

［8］徐玉琴，张丽，王增平，等．基于多智能体遗传算法并考虑分布式电源的配电网大面积断电供电恢复算法［J］．电工技术学报，2010（4）：135-141.

［9］王超学，崔杜武，崔颖安，等.使用基于中医思想的蚁群算法求解配电网重构［J］.中国电机工程学报，2008（7）：13-19.

［10］郇嘉嘉，黄少先.基于免疫原理的蚁群算法在配电网恢复中的应用［J］.电力系统保护与控制，2008（17）：89-93.

［11］孙雅明，杜红卫.可靠性知识与最优评估配电网故障恢复（二）最优评估［J］.电力系统自动化，2003（13）：36-39.

［12］黄弦超，张粒子，TAYLOR G.考虑负荷控制的配电网故障恢复［J］.电力系统自动化，2010（17）：22-26.

［13］黄弦超，TAYLOR G.基于节点深度编码技术的配电网故障恢复［J］.电力系统自动化，2011（6）：40-39.

［14］宋军英，何聪，李欣然，等.基于特征指标降维及熵权法的日负荷曲线聚类方法［J］.电力系统自动化，2019（20）：65-76.

［15］孙晓东，焦玥，胡劲松．基于组合权重的灰色关联理想解法及其应用［J］．工业工程与管理，2006（1）：62-66.

［16］吴耀文，马溪原，方华亮，等.大规模风电特高压专用通道落点优选方法［J］.中国电机工程学报，2012（1）：9-16.

［17］SAVIERJ S，DAS D.Impact of network reconfiguration on loss allocation of radial distribution systems ［J］.IEEE Transactions on Power Delivery，2007（4）：2473-2480.

（编辑 王雪芬）

Research on distribution network service restoration based on entropy weight and adaptive load coding strategy

YUAN Jie1， YAO Yuhai1， WANG Ting1， ZHANG Yi1， SUN Yongwen2

（1.State Grid Beijing Electric Power Company， Beijing 100031， China;

2.Beijing Crehoi Sci&Thch Co.， Ltd.， Beijing 102299， China）

Abstract： Objective weights were difficult to be made reasonably in traditional evaluation method of service restoration. In this paper the synthetic weight was used to evaluate the service restoration plans for the swarm intelligence algorithm. Besides the traditional swarm intelligence algorithm is difficult to deal with the problem that the load cannot be recovered completely， this paper proposed a load shedding strategy to ensure each individual of the group is feasible in the point of electricity. Finally a numerical example shows that the proposed method can effec-tively obtain the optimal plan of distribution network service restoration.

Key words： service restoration; distribution network; swarm intelligence algorithm; entropy weight; adaptive load coding strategy