一个几何模型的等角性质及其应用

切线是平面几何中最基本的模型之一，与之相关的最熟悉的是切割线定理，笔者在竞赛培训过程中，探究到一个几何模型的等角性质.

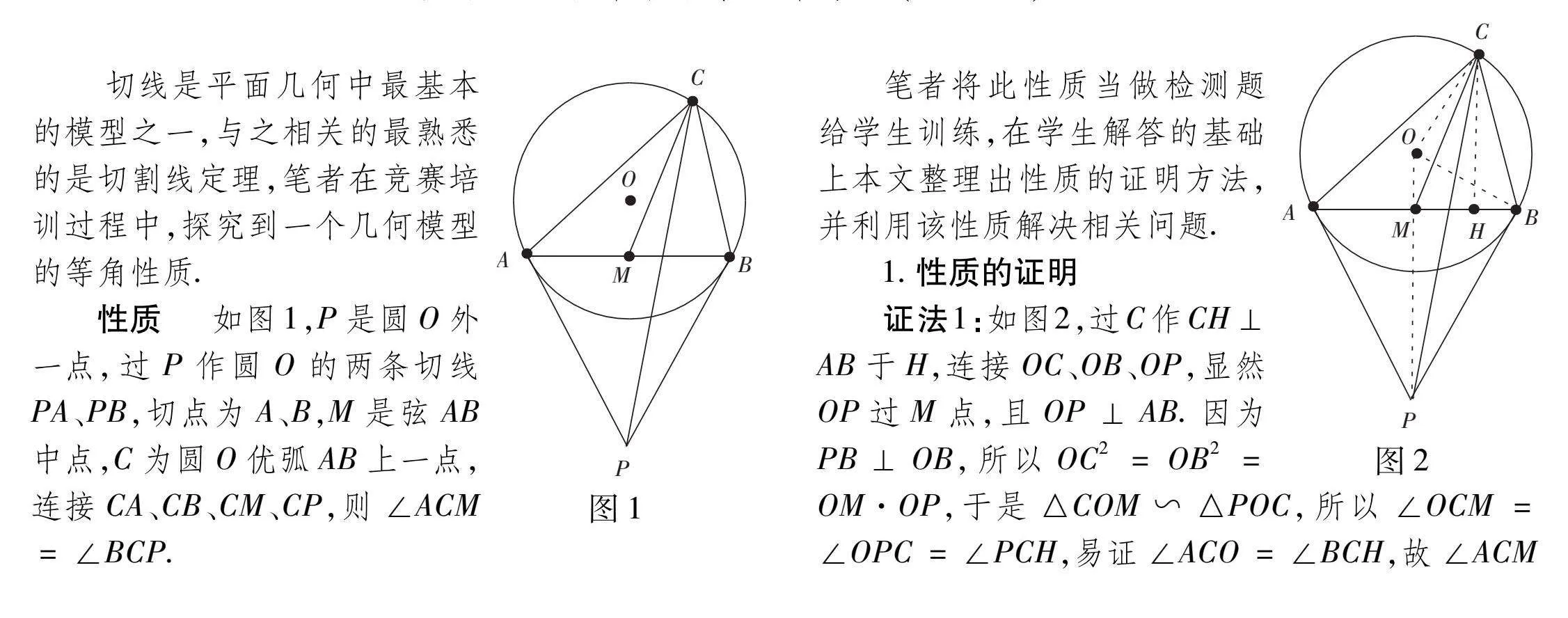
性质 如图1，P是圆O外一点，过P作圆O的两条切线PA、PB，切点为A、B，M是弦AB中点，C为圆O优弧AB上一点，连接CA、CB、CM、CP，则∠ACM=∠BCP.

笔者将此性质当做检测题给学生训练，在学生解答的基础上本文整理出性质的证明方法，并利用该性质解决相关问题.

1.性质的证明

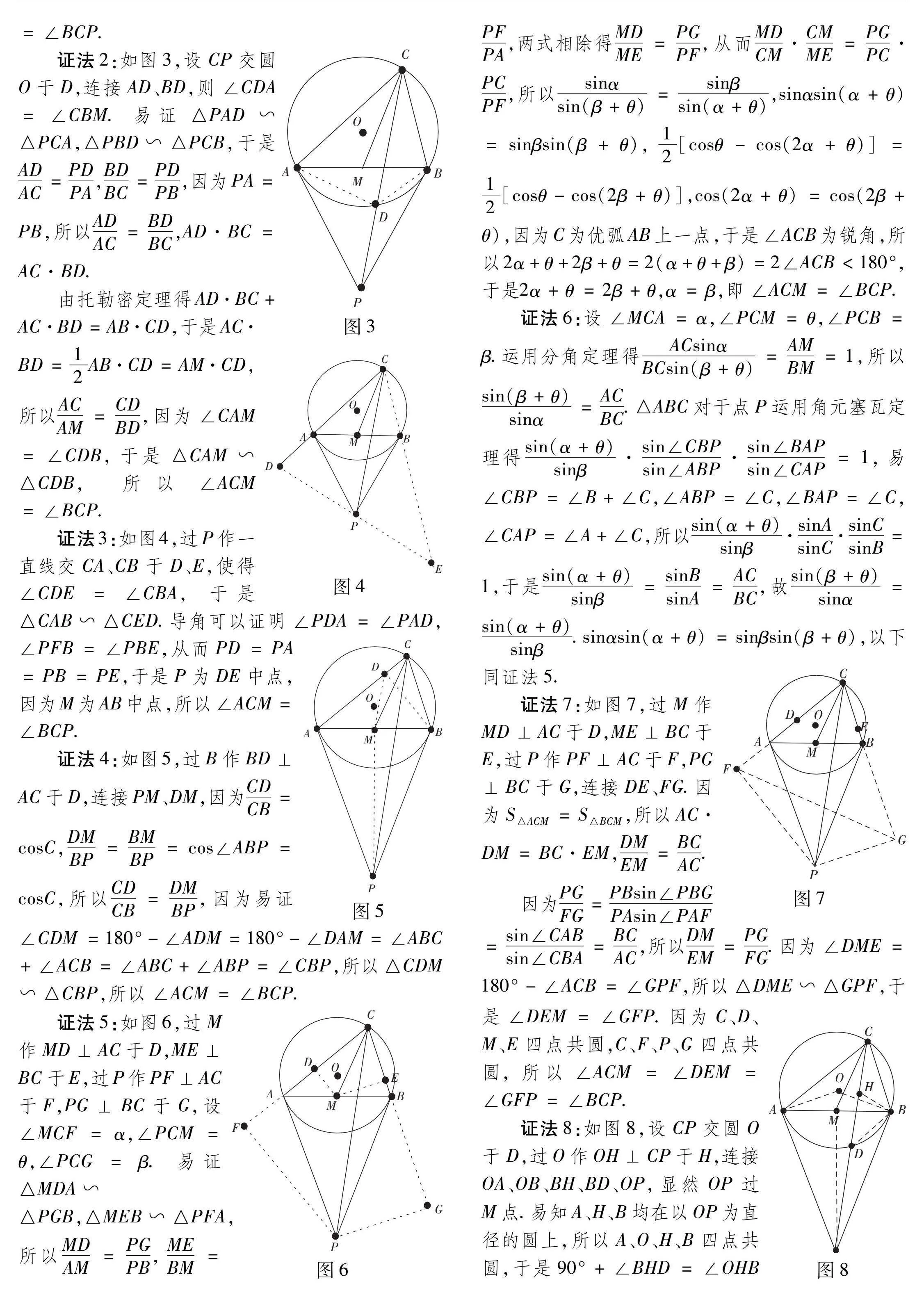
证法1：如图2，过C作CH⊥AB于H，连接OC、OB、OP，显然OP过M点，且OP⊥AB.因为PB⊥OB，所以OC2=OB2

=OM·OP，于是△COM∽△POC，所以∠OCM=∠OPC=∠PCH，易证∠ACO=∠BCH，故∠ACM=∠BCP.

证法2：如图3，设CP交圆O于D，连接AD、BD，则∠CDA=∠CBM.易

证△PAD∽△PCA，△PBD∽△PCB，于是ADAC=PDPA，BDBC=PDPB，因为PA=PB，所以ADAC=BDBC，AD·BC

=AC·BD.

由托勒密定理得AD·BC+AC·BD=AB·CD，于是AC·

BD=12AB·CD=AM·CD，所以ACAM=CDBD，因为∠CAM=∠CDB，于是△CAM∽△CDB，所以∠ACM=∠BCP.

证法3：如图4，过P作一直线交CA、CB于D、E，使得∠CDE=∠CBA，于是△CAB∽△CED.导角可以证明∠PDA=∠PAD，∠PFB=∠PBE，从而PD=PA=PB=PE，图5于是P为DE中点，因为M为AB中点，所以∠ACM=∠BCP.

证法4：如图5，过B作BD⊥AC于D，连接PM、DM，因为CDCB=cosC，

DMBP=BMBP=cos∠ABP=cosC，所以CDCB=DMBP，因为易证∠CDM=180°－∠ADM=180°－∠DAM=∠ABC+∠ACB

=∠ABC+∠ABP=∠CBP，所以△CDM∽△CBP，所以∠ACM=∠BCP.图6

证法5：如图6，过M作MD⊥AC于D，ME⊥BC于E，

过P作PF⊥AC于F，PG⊥BC于G，

设∠MCF=α，∠PCM=θ，∠PCG=β.易证△MDA∽△PGB，△MEB∽△PFA，所以MDAM=PGPB，MEBM=PFPA，两式相除得MDME=PGPF，从而MDCM·CMME=PGPC·PCPF，所以sinαsin（β+θ）=sinβsin（α+θ），sinαsin（α+θ）=sinβsin（β+θ），12［cosθ－cos（2α+θ）］=12［cosθ－cos（2β+θ）］，cos（2α+θ）=cos（2β+θ），因为C为优弧AB上一点，于是∠ACB为锐角，所以2α+θ+2β+θ=2（α+θ+β）=2∠ACB<180°，于是2α+θ=2β+θ，α=β，即∠ACM=∠BCP.

证法6：设∠MCA=α，∠PCM=θ，∠PCB=β.运用分角定理得ACsinαBCsin（β+θ）=AMBM=1，所以sin（β+θ）sinα=ACBC.△ABC对于点P运用角元塞瓦定理得sin（α+θ）sinβ·sin∠CBPsin∠ABP·sin∠BAPsin∠CAP=1，易∠CBP=∠B+∠C，∠ABP=∠C，∠BAP=∠C，∠CAP=∠A+∠C，所以sin（α+θ）sinβ·sinAsinC·sinCsinB=1，于是sin（α+θ）sinβ=sinBsinA=ACBC，故sin（β+θ）sinα=sin（α+θ）sinβ.sinαsin（α+θ）=sinβsin（β+θ），以下同证法5.图7

证法7：如图7，过M作MD⊥AC于D，ME⊥BC于E，过P作PF⊥AC于F，PG⊥BC于G，

连接DE、FG.因为S△ACM=S△BCM，所以AC·DM=BC·EM，DMEM=BCAC.

因为PGFG=PBsin∠PBGPAsin∠PAF=sin∠CABsin∠CBA

=BCAC，所以DMEM=PGFG.因为∠DME=180°－∠ACB=∠GPF，

所以△DME∽△GPF，于是∠DEM=∠GFP.因为C、D、M、E四点共圆，C、F、P、G四点共圆，所以∠ACM=∠DEM=∠GFP=∠BCP.

证法8：如图8，设CP交圆O于D，过O作OH⊥CP于H，连接OA、OB、BH、BD、OP，显然OP过M点.易知A、H、B均在以OP为直径的圆上，所以A、O、H、B四点共圆，

于是90°+∠BHD=∠OHB=180°－∠OAB=180°－（90°－∠ACB）=90°+∠ACB，从而∠BHD=∠ACB，

因为∠HDB=∠CAB，所以△HDB∽△CAB，于是HDBD=ACAB，2HDBD=AC12AB，即CDBD=ACAM，

因为∠CDB=∠CAM，所以△CDB∽△CAM，故∠ACM=∠BCP.

证法9：如图9，在PM上取一点D使得A、M、C、D四点共圆，则∠CDM=∠CAM=180°－（∠ACB+∠ABC）=180°－（∠ABP+∠ABC）=180°－∠CBP，所以C、D、P、B四点共圆，从而∠PCB=∠PDB，因为∠ACM=∠ADM，易知∠PDB=∠ADM，所以∠ACM=∠BCP.

2.性质的应用

例1 （2022年韩国数学奥林匹克决赛）如图10所示，锐角△ABC外心为O，三条高分别为AD、BE、CF.过B、C分别作⊙O的切线，交于点P.过P作EF垂线与AD交于点Q.过A作AR⊥于R.求证：DR//OQ.

证明：如图11所示，因为O为

△ABC的外心，AD、BE、CF为三条高，所以AO⊥EF，又AR⊥EF，则知A、R、O三点共线，且EF与BC逆平行，于是有ARAD=AEAB=AFAC=cos∠BAC.连接OB，设OP交BC于点M，则OB⊥BP，OM⊥BC，又PQ⊥EF，易知四边形AOPQ为平行四边形.因为O为△ABC的外心，AD⊥BC，则易得∠BAD=∠CAO，

又PB，PC为圆O的切线，M为BC的中点，由性质知∠BAP=∠CAM，所以∠OAM=∠QAP，

又∠AOM=∠AQP，所以△AOM∽△AQP，所以AOAQ=AMAP=OMQP.结合OA=OB=QP，∠BOM=∠PBC=∠BAC，于是有AOAQ=OMQP=OMOB=cos∠BOM=cos∠BAC.从而ARAD=AOAQ，所以DR//OQ.

例2 （2022年巴尔干数学奥林匹克）

如图12所示，锐角△ABC满足CA≠CB，其外接圆为ω，外心为O，过B，A作ω的切线交于点X，过点C作AB的平行线交XA延长线于点Z.OY⊥XC于点Y.求证：直线YZ平分线段AC.

证明：如图13所示，

设OX、CX与AB、ω分别交于点S、T，连接AO、AY、AT、BO、CS.

易知OA⊥AX，OB⊥BX，OY⊥CT，S是AB中点，A、X、B、Y、O五点共圆.从而∠BAY=∠BXY.由于XA、XB为ω的两条切线，S为AB的中点，则有∠ACS=∠BCT=∠BAT，∠BCS=∠ACT，∠CBK=∠BXY+∠BCT，又∠CBK=∠BAC=∠BAY+∠CAY，于是∠CAY=∠BCT=∠BAT.所以∠CAB=∠TAY，结合∠ATY=∠ABC，可知∠AYT=∠ACB=∠XAB=∠AZC，因此A、Y、C、Z四点共圆，可得∠AZY=∠ACY=∠XAT，从而AT//ZY，注意到Y为CT的中点，所以YZ平分线段AC.图14

例3 如图14所示，已知△ABC（AB<AC）的

外接圆Γ在点B、C处的切线相交于点D，E在CB延长线上，使得AE⊥AD.点F为DE的中点.求证：FA为Γ的切线.

证明：如图15所示，设Γ的圆心

为O，AD交Γ于点N，连接OD交BC于点M，再连接AM，CN.因为DB，DC与圆O相切，且M为BC的中点，由性质知∠BAM=∠CAN.结合∠ABM=∠ANC，所以△ABM∽△ANC，从而有∠AMB=∠ACN，又因为AE⊥AD，F是DE的中点，注意到A，M，D，E四点共圆，AF=DF=EF，∠FAD=∠ADF=∠AMB，于是∠FAN=∠ACN，所以FA为Γ的切线.