基于数据驱动的锂电池健康状态预测

摘要： 针对传统基于数据驱动锂电池健康状态预测模型所存在的精确度低、鲁棒性差等问题，构建了一个融合非线性与线性特征的时序预测模型，其中多尺度一维卷积神经网络串联双向门控循环神经网络形成非线性时序预测分支，自回归模型构成线性分支。两个分支并联，最终通过全连接层输出预测结果。模型具备非线性部分的泛化能力和线性部分的记忆能力，对输入的幅值变化更加灵敏，并采用鲸鱼优化算法寻找最优模型超参数。通过对比现有模型以及消融实验验证了所提模型的有效性。

关键词： 电池健康状态；双向门控循环神经网络；自回归模型；鲸鱼优化算法

中图分类号： TM912;TP183文献标识码： A

A Data-driven Model for Prediction of Lithium Battery State of Health

CUI Xiaokai，WANG Qingzhi，LIU Qipeng

（College of Automation，Qingdao University，Qingdao 266071，China）

Abstract：To address the problems of low accuracy and poor robustness of traditional data-driven battery state of health prediction model， this paper develops a time series prediction model fusing both nonlinear and linear branches. The nonlinear time series prediction branch is formed by a one-dimensional convolutional neural network with a multi-size parallel structure in series with a bidirectional gated recurrent neural network， and the linear branch is constructed by an autoregressive model. Two branches in parallel output prediction results through a fully connected layer. The above prediction model has the generalization ability of the nonlinear part and the memory ability of the linear part， and is more sensitive to the change of input amplitude. The whale optimization algorithm is used to effectively search the optimal model hyper-parameters. The effectiveness and superiority of the linear nonlinear fusion prediction model proposed in this paper are verified by comparing existing models and ablation experiments.

Keywords： battery state of health; bidirectional gated recurrent neural network; autoregressive model; whale optimization algorithm

0 引言

近年来，随着锂电池在新能源汽车、消费电子等产品中的广泛引用，锂电池的健康状态（State of Health，SOH）监测也成为人们关注的热点。已有研究表明，锂电池最大容量下降到出厂额定容量的70%～80%时，会出现明显的性能失效和安全性失效，严重影响设备的正常使用［1］。对于SOH的预测通常包括基于经验、基于等效模型以及基于数据驱动的方法。基于经验的方法是利用电池使用过程中的经验知识，依据统计规律给出电池容量的粗略估计，适用于经验知识充分的特定场景中［2］。基于等效模型的方法更倾向于构建机理模型。例如，文献［3］通过基于机理的单粒子模型来推演每一个老化因素对电池状态变化规律的影响。基于数据驱动方法则是利用电池状态数据拟合线性或非线性模型来预测电池当前状态。例如，文献［4］构建了一个维卷积神经网络模型，将电池电压、电流和温度时序数据作为输入，并通过数据增强预测输出电池容量，显著降低了模型预测的平均绝对误差；文献［5］通过卷积网络提取高维数据特征，并输入到长短时记忆网络中，将历史信息有效的映射到预测结果中。

基于经验以及基于等效模型的方法往往需要电化学、物理学理论的支持来构建物理模型，建模过程繁琐且无法支持电池状态的实时预测。而基于数据驱动的方法则直接利用电池状态的历史数据提取特征，从而更加高效地实现预测。但是，现有的数据驱动模型越来越强调模型非线性预测的效果，使得模型越来越复杂，导致模型训练困难且泛化性较差。

为了解决上述问题，进一步提高模型预测精度，本文基于数据驱动方法，从特征数据线性和非线性两方面出发，通过深度学习模型来发掘电池时序特征的非线性属性，通过线性自回归模型发掘特征的线性属性，最后并联两分支构建完整预测网络。本文主要贡献：1）为了提高模型对于时序特征的提取能力，本文采用Inception结构［6］构建了一维卷积网络层，通过并联不同卷积核尺寸的一维卷积网络（One-dimensional Convolutional Neural Network，1DCNN）［5］实现不同感受野的特征提取，然后串联双向门控循环神经网络（Bidirectional Gated Recurrent Neural Network， BiGRU）［7］使模型可以从深度和宽度两个维度来提取特征，以此来提高对时序依赖关系的提取能力；2）针对预测模型的复杂化导致的预测精度下降问题，本文采用自回归模型（Autoregressive Model， AR）［8］来拟合电池容量数据的线性自回归过程，通过线性和非线性模块的融合，提高整体模型对于输入响应的灵敏度，从而提高模型的预测精度；3）针对模型调参困难、模型训练效率差等问题，本文采用鲸鱼优化算法（Whale Optimization Algorithm， WOA）［9］有效地搜索最优模型的超参数。

1 预测模型介绍

1.1 模型整体框架

本文构建的锂电池健康状态预测模型包含非线性和线性两个并联的分支，其中非线性分支由Inception构建1DCNN网络，对输入特征进行多尺度特征提取，输入到两层BiGRU网络进行时序分析，再通过全连接层得到非线性部分的输出值；线性分支由全连接层来实现线性的自回归（AR）过程。两分支预测结果叠加得到模型最终的输出。模型结构如图1所示。

1.2 一维卷积神经网络

本文采用一维卷积神经网络（1DCNN）［5］对传入时序数据进行特征提取。相比于常见的二维卷积，一维卷积通过固定尺寸的卷积核按固定轴方向对整个数据进行滑动特征提取，将低维的不易分离的特征映射为高维表达能力更强的特征，更适合用来分析时序数据。

在网络结构设计中，本文采用Inception［6］结构来搭建卷积模块，如图2所示。Inception网络结构通过并联不同尺寸的卷积模块增加模型宽度，既可以提供不同感受野信息，又实现了以较少的模型训练参数来获得更强的模型表现力。

在图2中，n表示输入时序数据的特征数，1、3、5表示卷积所处理的时间步长，拼接层表示基于特征维度的数据叠加结构。3种感受野的一维卷积网络可以用来提取不同时间步长数据之间的特征关系，并将特征拼接送入后续网络结构进行深层特征提取。

1.3 双向门控循环神经网络

循环神经网络（RNN）系列模型被广泛应用于时序数据预测领域，其利用神经元之间的相互交流预测时序间的连贯特征，显著提高了模型预测精度。本文采用了更加高效的双向门控循环神经网络（BiGRU）［7］，通过发掘序列数据中的前语义和后语义来共同决定预测结果。图3展示了两个GRU模块组成的双向结构，其中输入xt经由两模块处理后输出正向隐层状态ht和反向隐层状态ht，经过加权求和后输出t时刻网络层的隐层状态ht，公式为

ht=f（w1xt+w2ht-1）（1）

ht=f（w3xt+w5ht+1）（2）

ht=wtht+vtht+bt（3）

其中，f对应在特定方向上的GRU运算，w1，w2，w3，w4分别表示不同方向GRU模块输入和隐层状态对应的权重系数，wt，vt，bt分别表示前向隐层状态权重、反向隐层状态权重以及加权求和过程中的偏置向量。通过线性组合正反两方向的GRU输出结果，使得模型预测可以充分挖掘前后语义信息，提高预测准确度。

1.4 线性自回归模型

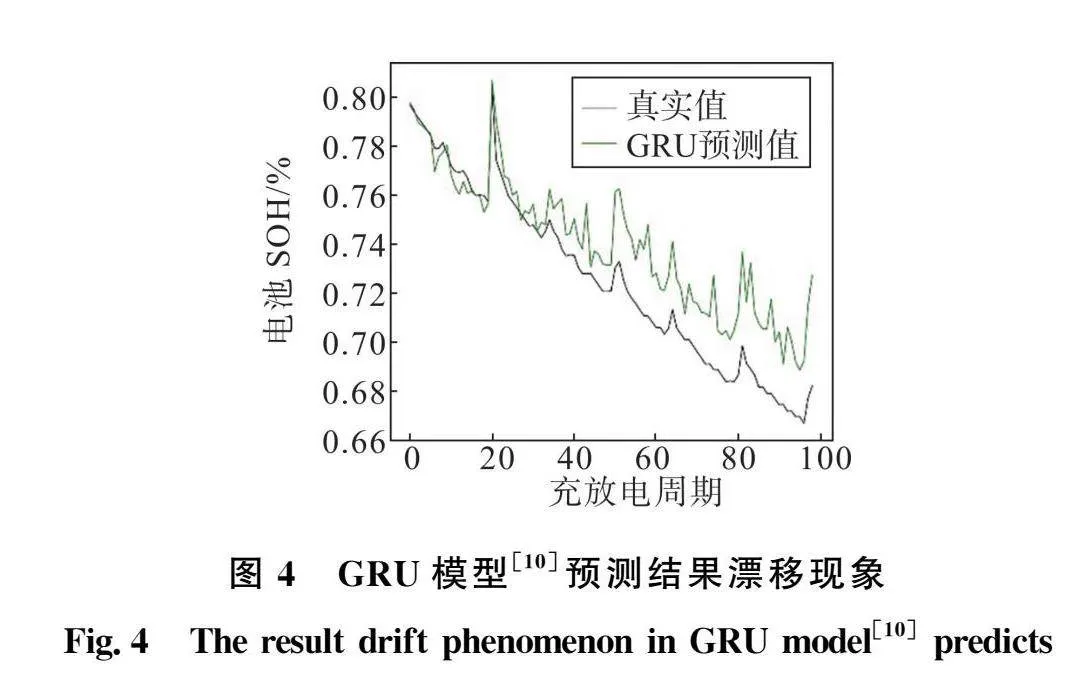
现有的SOH预测模型中，随着网络层数的增加，非线性预测能力增强的同时梯度值反向传播难度加大，模型对输入数据的幅值变化敏感度降低。例如，用文献［10］所搭建的GRU模型预测电池SOH实验时发现，模型会随着充放电周期的增加出现不同程度的预测值漂移现象，如图4所示。

为了解决上述问题，本文利用了数据的线性特征来约束预测结果的变化趋势。具体地，采用自回归模型［8］将数据特征线性组合，其公式为

Xt=c+∑pi=1φiXt-i+ t（4）

其中，c为常数项， t为随机噪声值，φi对应为序列Xt-i的线性相关系数，p表示相关序列的时间跨度。线性模型将当前时刻的输出表示为历史时刻值的线性加权值。在本文中，使用线性的全连接层来模拟自回归模型，将给定时间步长的数据打包输入全连接层实现自回归。

1.5 超参数寻优

模型超参数，例如网络层数、迭代次数、学习率等，直接影响模型的训练和预测效果。常用的网格搜索［11］方法存在调参的盲目性和低效性的缺点。本文采用鲸鱼优化算法（WOA）［9］来优化模型调参过程，按照明确的优化策略对目标参数进行修正，更加高效地实现模型参数寻优。相比于其他智能优化算法，WOA算法优点在于操作简单，调整的参数少以及跳出局部最优的能力强。关于WOA算法的详细介绍可参考文献［9］。

在本文中，将网络的学习率、训练次数、批处理大小、第一层BiGRU隐层节点数、第二层BiGRU隐层节点数、非线性分支的全连接层节点数等6个参数作为WOA优化变量。适应度函数为预测值与实际值的均方差，优化目标是最小化适应度函数。算法整体步骤：1）分析数据不同特征对容量变化相关性系数，将满足条件的数据特征作为模型的输入；2）将数据按设定的时间跨度打包成时序数据，对数据进行归一化处理并划分为训练集和测试集，构建可通过迭代优化的神经网络模型并初始化模型参数；3）设定模型待优化的超参数为WOA算法中鲸群位置坐标；4）训练模型，计算模型的适应度函数，更新WOA算法中的变量；5）重复上述WOA和模型训练过程至指定最大迭代次数，WOA算法搜索结束，得到最优超参数，用于训练最终的模型。

2 方案验证与结果分析

2.1 评价指标

本文任务是预测电池的健康状态，即通过现有充放电数据预测未来电池容量。电池容量定义［12］：稳定充电条件下，充电电流降低至20mA，电池所能存储的最大电量安时（Ah）数。根据电池容量定义电池健康状态SOH为

SOH=CmaxCrated×100%（5）

其中，Cmax表示完全充满时电池的当前最大容量，Crated表示电池出厂时的额定容量。

本文选用均方根误差（Root-mean-square deviation， RMSE）、平均绝对误差（Mean Absolute Error， MAE）、决定系数（Coefficient of determination，R2）以及平均绝对百分比误差（mean absolute percentage error， MAPE）指标进行定量分析，定义为

RMSE= 1n∑ni=1（yi-y︿i）2（6）

MAE=1n∑ni=1（yi-y︿i）（7）

R2=1-∑ni=1（y︿i-yi）2∑ni=1（y-i-yi）2（8）

MAPE=100%n∑ni=1y︿i-yiyi（9）

其中，yi，y︿i，y-i分别表示第i组数据实际电池容量、预测电池容量以及实际电池容量均值。

2.2 数据预处理

选用NASA电池数据集［12］中B0005、B0006、B0007和B0018数据包为实验数据集（简称电池5，6，7和18）。数据集采集条件为：1）室温24°恒温场景下采集；2）充电过程以1.5A的恒定电流（CC）模式进行充电，直到电池电压达到4.2V，然后以恒定电压（CV）模式充电，直到充电电流降至20 mA；3）放电过程以2A的恒定电流（CC）模式进行放电，直到电池5、6、7和18的电压降到2.7V，2.5V，2.2V和2.5V；（4）终止条件：当电池达到寿命终止（End of Life， EOF）标准——额定容量下降30%，电池5，6，7和18的额定容量从2Ahr到1.4Ahr。

本文采用放电电压Tdv、充电电流Tccur以及电池容量Tcapacity作为模型特征。每次循环会以固定时间间隔记录两百次以上的放电电压和充电电流时序数据，同时每次循环结束后会保存一个电池容量数据。本文选用Tdv和Tccur两特征为模型非线性分支输入特征，例如表1中，（502，170，2）数据规格表示为：将两特征序列尾部170行数据打包为一个样本，共502个样本组成数据集。经验证明Tcapacity特征具有线性自回归性，因此我们将该特征作为模型线性分支的输入特征，例如表1中，（502，8，1）数据规格表示为：将包含当前时序电池容量值在内的8次连续时序数据打包为一个样本，共有502个样本组成数据集。我们使用下一个时间步的Tcapacity特征作为样本的标签，既模型待预测目标值。测试集由4组电池样本末端31组循环数据合并而成，不参与模型训练，数据结构如表1所示。

2.3 消融实验

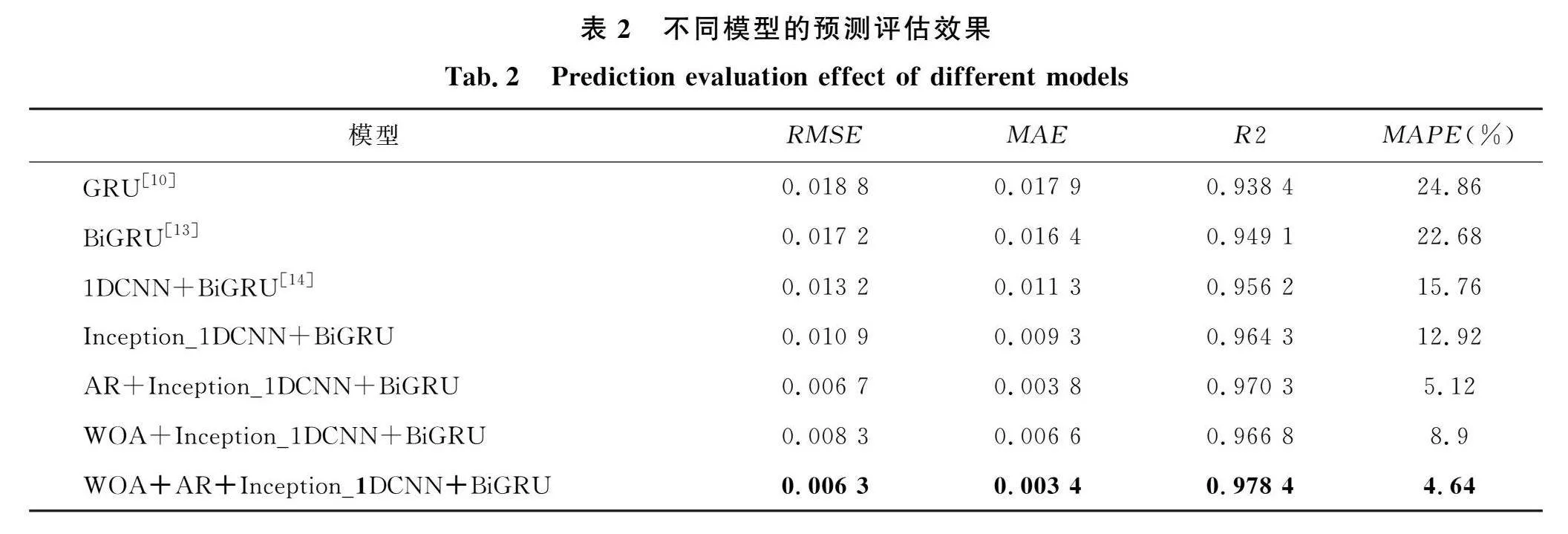
消融实验第1阶段对比非线性分支的预测效果，分别选取GRU［10］、BiGRU［13］、1DCNN+BiGRU［1415］以及本文的Inception_1DCNN+BiGRU模型，在输入数据集尺寸、网络参数相同前提下，得到如图5所示的预测结果，具体数值汇总于表2中。

图5a对比了GRU模型和BiGRU模型的SOH预测效果，BiGRU相比较GRU在RMSE、MAE和MAPE指标分别有8.5%、8.3%和8.7%的下降幅度。该实验表明，在时序预测问题中，正序和逆序数据特征均会对模型预测产生影响，可以发现并学习序列上下文信息来提高模型学习能力；图5b对比BiGRU模型和1DCNN-BiGRU模型的SOH预测效果，可以看到采用1DCNN的模型在部分区间预测精度明显高于后者，RMSE、MAE和MAPE指标分别有23.2%、31.1%和30.5%的下降幅度，说明对于序列值波动不大的区间，1DCNN可以帮助分析时间序列数据中的短期依赖关系，并提高模型的特征提取能力；图5c对比1DCNN-BiGRU模型和Inception_1DCNN-BiGRU模型的SOH预测效果，采用并联1DCNN结构的模型在整体上更精准地拟合了真实标签，RMSE、MAE和MAPE指标分别有17.4%、17.7%和18%的下降幅度，该实验表明，添加多尺度一维卷积模型后可以提取数据多感受野的特征，更好地捕捉到单一感受野可能遗漏的时间信息，相比较单一尺度模型特征提取能力更强。以上3组实验的决定系数R2均超过0.93，且Inception_1DCNN-BiGRU模型达到了最高的0.964 3，表示该模型对该数据集具有更强的解释力和预测能力，进一步证明了本阶段所采用的并联一维卷积结构和双向门控循环神经网络可以提高电池SOH预测模型的精度。

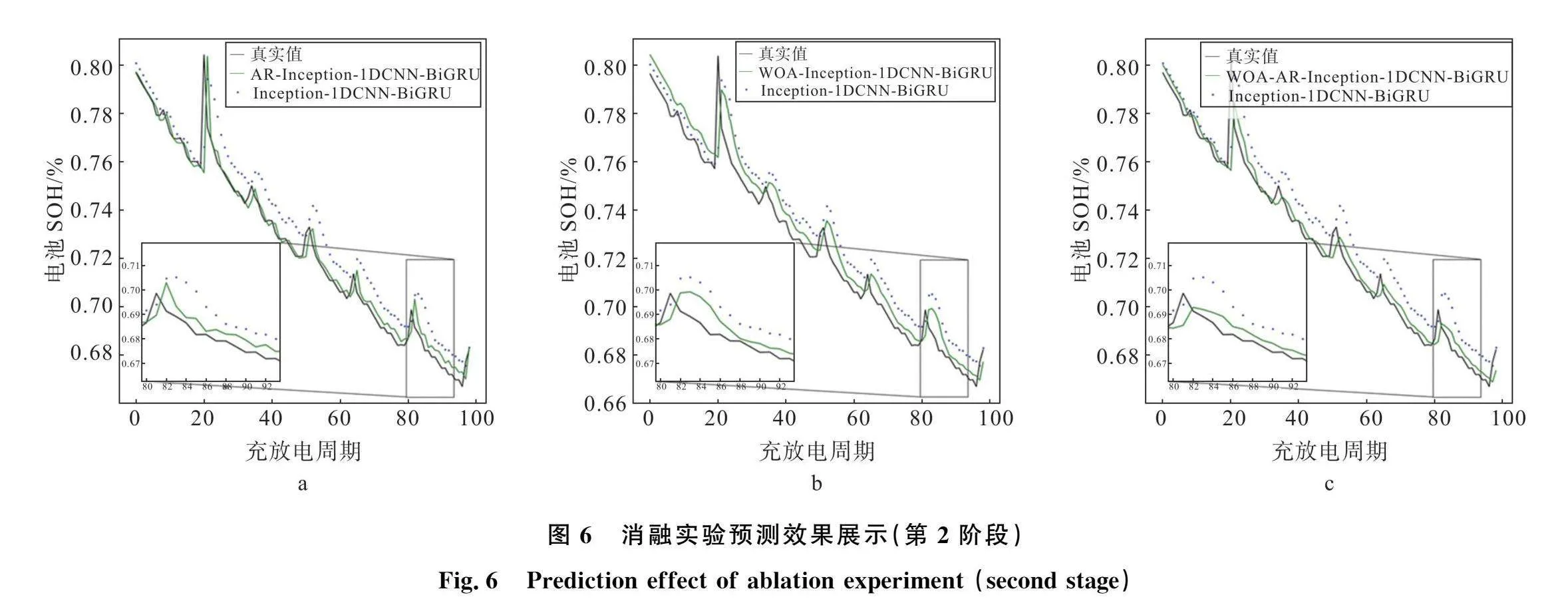
消融实验第2阶段以Inception_1DCNN加BiGRU模型为基准，以此来验证线性自回归模块（AR）和鲸鱼优化算法（WOA）对预测模型的影响，结果如图6所示。

图6a对比基准模型和添加AR模块的预测效果。添加AR模块后预测精度明显提升，RMSE、MAE和MAPE指标分别有38.5%、59.1%和60.4%的下降，表明通过发掘序列的线性特征可以对模型预测精度产生显著影响；图6b对比基准模型和添加WOA的预测效果。采用WOA之后，RMSE、MAE和MAPE相比于基准分别有23.9%、29%和31.1%的下降，表明通过WOA算法可以有效地实现寻找最优模型参数的目的，提高模型训练的效率；图6c为本文模型与基线模型的对比效果，RMSE、MAE和MAPE指标分别有42.2%、63.4%和64%的下降。实验表明，同时添加线性自回归模块（AR）和采用鲸鱼优化算法（WOA）相比较单独添加模块效果更好，且决定系数R2值为0.978 4为所有对比模型中最高的，表示相较对比模型来说本文模型对数据的解析和预测能力最好。

3 总结与展望

本文针对电池健康状态预测问题，提出了一种基于数据驱动的预测模型，通过Inception结构的一维卷积层与BiGRU网络层构建模型的非线性预测部分，通过线性自回归网络层构建模型的线性预测部分，最后利用鲸鱼优化算法搜索模型超参数。非线性模块可以挖掘多特征时序数据的深层抽象特征，提高了模型对于数据的泛化能力，而线性模块挖掘衰减曲线的线性特征，提高整体模型对于输入响应的灵敏度。基于实际数据的实验验证了模型的有效性。

未来工作中，希望通过电池时序特征预测电池容量的衰减曲线，进一步将预测任务转化为电池剩余寿命（RUL）的预测任务。在模型方面，可进一步考虑自注意力机制对电池容量衰减预测的影响。在数据方面，则可以考虑更多相关性强的电池特征数据对预测精度的影响。

参考文献：

［1］王其钰， 王朔， 周格， 等. 锂电池失效分析与研究进展［J］. 物理学报， 2018， 67（12）： 279290.

WANG Q Y， WANG S， ZHOU G， et al. Progress on the failure analysis of lithium battery ［J］. Acta Physica Sinica， 2018， 67（12）： 279290.

［2］罗伟林， 张立强， 吕超， 等. 锂离子电池寿命预测国外研究现状综述［J］. 电源学报， 2013 （1）： 140144.

LUO W L， ZHANG L Q， LV C， et al. Review on foreign status of life prediction of lithium-ion batteries ［J］. Journal of Power Sources， 2013 （1）： 140144.

［3］ZHANG Q， WHITE R E. Capacity fade analysis of a lithium-ion cell［J］. Journal of Power Sources， 2008， 179（2）： 793798.

［4］李超然，肖飞，樊亚翔，杨国润，唐欣.基于卷积神经网络的锂离子电池SOH估算［J］.电工技术学报，2020，35（19）：41064119.

LI C R， XIAO F， FAN Y X， et al. An approach to lithium-ion battery SOH［J］. Transactions of China Electrotechnical Society，2020， 35（19）： 41064119.

［5］倪水平，李慧芳.基于一维卷积神经网络与长短期记忆网络结合的电池荷电状态预测方法［J］.计算机应用，202 41（5）：15141521.

NI S P， LI H F. Battery state-of-charge prediction method based on one-dimensional convolutional neural network combined with long short-term memorynetwork［J］. Computer Applications， 202 41（5）： 15141521.

［6］SZEGEDY C， LIU W， JIA Y， et al. Going deeper with convolutions［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York： IEEE， 2015： 19.

［7］LIU F， ZHENG J， ZHENG L， et al. Combining attention-based bidirectional gated recurrent neural network and two-dimensional convolutional neural network for document-level sentimentclassification［J］. Neurocomputing， 2020， 371： 3950.

［8］PARK J， LEE M， KIM G， et al. Integrated approach based on dual extendedKalman filter and multivariate autoregressive model for predicting battery capacity using health indicator and SOC/SOH［J］. Energies， 2020， 13（9）： 2138.

［9］MIRJALILI S， LEWIS A. The whale optimization algorithm［J］. Advances in Engineering Software， 2016， 95： 5167.

［10］ 曹广华，赵中林，许昀昊.基于GRU的锂电池组健康状态预测研究［J］.吉林大学学报（信息科学版），2022，40（2）：181187.

CAO G H， ZHAO L Z， XU Y H.Research on health state prediction of lithium battery pack based on GRU［J］. Journal of Jilin University （Information Science Edition）， 2022， 40（2）：181187.

［11］ 王鑫，吴际，刘超，杨海燕，杜艳丽，牛文生.基于LSTM循环神经网络的故障时间序列预测［J］.北京航空航天大学学报，2018，44（4）：772784.

WANG X， WU J， LIU C， et al. Exploring LSTM based recurrent neural network for failure time series prediction［J］. Journal of Beijing University of Aeronautics and Astronautics， 2018， 44（4）： 772784.

［12］ National Aeronautics and Space Administration Prognostics Center of Excellence.PCoE datasets［EB/OL］.［20221006］.https：//ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/#battery.

［13］ 朱元富，贺文武，李建兴，等.基于Bi-LSTM/Bi-GRU循环神经网络的锂电池SOC估计［J］.储能科学与技术，202 10（3）：11631176.

ZHU Y F， HE W W， LI J X， et al. Estimation of SOC of lithium battery based on Bi-LSTM/Bi-GRU recurrent neural network［J］. Energy Storage Science and Technology， 202 10（3）：11631176.

［14］ 张国豪， 刘波. 采用 CNN 和 Bidirectional GRU 的时间序列分类研究［J］. 计算机科学与探索， 2019， 13（6）： 916.

ZHANG G H， LIU B.Research on time series classification using CNN and Bidirectional GRU［J］. Journal of Frontiers of Computer Science and Techno， 2019， 13（6）： 916.

［15］ 周键. 测控专业综合实验教学改革和实践［J］. 智库时代，2021（42）：104106，145.

ZHOU J. Comprehensive experimental teaching reform and practice of measurement and control specialty ［J］ Think Tank Times， 2021 （42）： 104106，145.

（责任编辑 李 进）