高低阶耦合网络的鲁棒性研究

摘要： 为了深入理解现实网络系统中的相互依赖关系，解决复杂网络及其高阶网络面临的级联故障问题。提出了一种高低阶耦合网络模型，该模型用于描述复杂网络（低阶网络）及其高阶组织（高阶网络）之间的相互依赖。通过对高低阶耦合网络进行随机攻击来分析其脆弱性。研究表明，与单独的低阶网络相比，高低阶耦合网络在面对随机攻击时表现出更高的脆弱性。这一结果强调了在设计和管理复杂网络系统时考虑高低阶网络相互依赖关系的重要性，尤其是在防止级联故障时需要特别关注这些相互依赖结构的脆弱性。

关键词： 高阶网络；相互依赖网络；级联失效；鲁棒性

中图分类号： N94;O157 文献标识码： A

Study on the Robustness of High-low-order Coupling Networks

ZHANG Chengjun，YAO Hui， LEI Yi，XIA Denghui，LI Qi，SHEN Xinyu，QIAN Ming，YU Wenbin

（Department of Computer and Software， Nanjing University of Information Science and Technology， Nanjing 210044， China）

Abstract：This paper proposes a high-low-order coupled network model to gain a deeper understanding of the interdependent relationships in real-world network systems and address the cascade failure issues faced by complex networks and their higher-order networks. This model describes the interdependencies between complex networks （lower-order networks） and their higher-order organizations （higher-order networks）. Their vulnerability is analyzed by subjecting the high-low-order coupled networks to random attacks. The study reveals that high-low-order coupled networks exhibit greater vulnerability to random attacks than standalone lower-order networks. This finding underscores the importance of considering the interdependencies between high and low-order networks in designing and managing complex network systems， particularly in preventing cascade failures， where special attention should be paid to the vulnerabilities of these interdependent structures.

Keywords： higher-order organization; interdependent network; cascading failure; robustness

0 引言

随着人类社会的快速发展，现实生活中的复杂网络变得更加庞大、复杂[1]。复杂网络理论在电力、生物、互联网等领域中的作用日益凸显，复杂网络发生故障会对社会生活产生巨大影响。为了解这些故障发生的原因，以及如何防止复杂网络发生故障，复杂网络的鲁棒性研究成为网络科学中的研究重点[23]。随着网络科学的不断发展，许多具有重要理论价值的网络模型被提出[49]，例如：无标度网络模型、小世界网络模型等，这些网络模型的研究极大推动了复杂网络鲁棒性研究的发展。过去几十年内，复杂网络鲁棒性研究进展大致分为两个阶段：第1阶段为单个网络的鲁棒性研究。Albert等[10]首先对单个网络进行了随机攻击和蓄意攻击，研究结果表明无标度网络对随机攻击的容忍能力很高，对蓄意攻击的容忍能力很差。Cohen等[11]在Albert等人工作的基础上，采用渗流理论，对无标度网络遭受攻击后的相变点进行研究，研究结果表明即使网络中的大部分节点因随机攻击而失效，网络中仍然存在能够正常工作的巨分量。基于Albert[10]和Cohen等[1112]的研究成果，学者们对单个网络的鲁棒性进行了更加深入的研究。例如，Cohen等[12]对无标度网络和随机网络的鲁棒性进行研究，他们详细分析了不同程度的蓄意攻击对网络鲁棒性的影响，从理论上证明了无标度网络在蓄意攻击下具有脆弱性。Frutos等[13]研究了西班牙最大的马德里地铁网络的鲁棒性，研究结果表明马德里地铁网络比其他交通网络更容易受到攻击。第2阶段为相互依赖网络的鲁棒性研究，2010年，Buldyre等[14]开创性地提出了相互依赖网络模型，并对相互依赖网络的鲁棒性进行研究。现实中的网络普遍存在着依赖关系，相互依赖网络的鲁棒性研究具有很强的现实意义。Parshani等[15]在Buldyre的研究基础上提出了部分依赖网络模型，依赖网络中的节点可能不是全部相互依赖，仅仅是部分节点相互依赖，并且发现部分依赖网络的鲁棒性更强。之后，Parshani等[16]发现网络的依赖关系不仅存在于依赖网络中，单个网络中也可能存在相互依赖关系，单个网络中的部分节点可能相互依赖，存在相互依赖连边，因此提出了含有依赖边的单个网络模型。此后更多的依赖网络模型被提出，相互依赖网络的基本理论也越发完善，也为今后的相互依赖网络的研究提供了理论基础[1721]。

上述的鲁棒性研究都是在“点—边”为基本单元的低阶网络上展开的，低阶网络往往会忽视节点之间的高阶交互关系，随着对现实世界的不断深入探索，学者们发现在真实网络中，节点个体之间不仅存在二元交互关系，也广泛存在多个节点同时（或以特定顺序）进行交互，即高阶交互关系。例如，在社交网络中，合作关系往往同时发生在多个个人之间，比如多名学者共同完成一篇科研文章。而Benson等[22]提出的基于模体的高阶网络就能够体现这些高阶交互关系，同时高阶网络对网络的功能至关重要。过去，学者们都是将低阶网络和高阶网络孤立起来研究，鉴于此，本文针对低阶网络和高阶网络之间的依赖关系，提出了一种无向网络的高低阶耦合网络模型，并对高低阶耦合网络的鲁棒性进行研究。

1 相关理论

1.1 高阶网络与模体

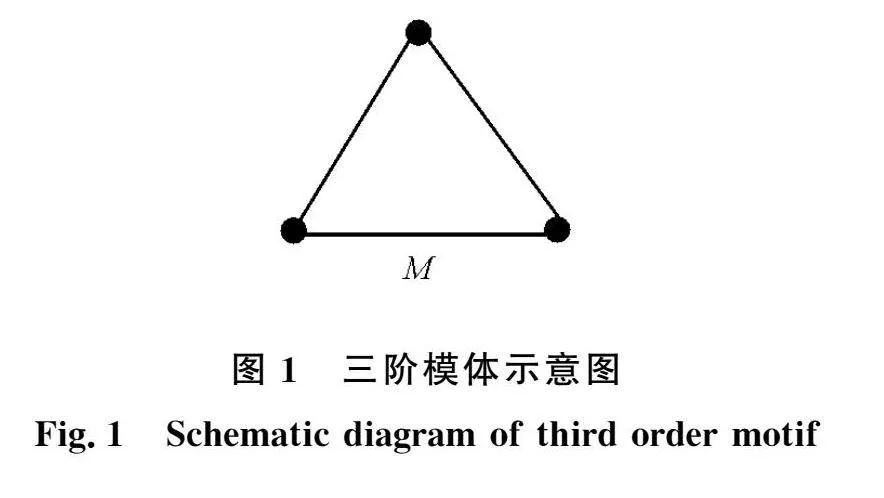
真实网络中存在着大量具有交互性、传递性的子图结构，这些子图结构又被称为网络模体，而真实网络存在以网络模体为基本单元的高阶网络结构[23]。网络模体是高阶网络的一种重要的表现形式[22]。根据模体中的节点数量，可以将模体分为三阶模体、四阶模体等。通常选择三阶模体或四阶模体作为基本研究单元，因为真实网络中更高阶模体的数量较少。在无向网络中，通常将3个节点组成的全连接结构作为三阶模体，如图1所示。

定义1 基于模体的邻接矩阵。给定一个模体M，对于拥有N个节点的网络G，其基于M的高阶邻接矩阵可以定义为WM=wijN×N，矩阵元素wij为G中连边eij在模体M中出现的次数，可定义为

wij=∑1，eij∈M且i≠j0，其他（1）

定义2 高阶网络。高阶网络表示为G=V，E，WM，其中V=vi|i=，…，n表示点集，E=eij|i，j=，…，m表示边集，eij是一条由节点vi指向节点vj的连边，WM是基于模体M的高阶邻接矩阵。

1.2 网络攻击策略和评价指标

1.2.1 攻击策略

本文采用随机攻击的方法对网络进行攻击，模拟网络中某个节点受到了意外情况而失效。在随机攻击方法中，随机移除网络中的节点，无需考虑节点之间的区别。

1.2.2 评价指标

网络发生故障或者遭受攻击时会分裂成多个规模不同的连通分量，其中规模最大的分量被称为巨型强连通分量。随机从网络中移除1-p的节点，以此来模拟网络的级联故障，当网络剩余节点p达到临界值pC时，网络开始出现巨型强连通分量。用PSymboleB@表示巨型强连通分量中节点个数与总节点的比例，PSymboleB@可表示为SymboleB@=nN（2）

其中，n为巨型强连通分量中的节点个数，而N为原始低阶网络的节点个数。对于低阶网络的渗流，也就是单个网络的渗流，通常表征为二阶渗流相变，可利用PSymboleB@（p）和p表示，其中PSymboleB@（p）为p的连续函数。本文基于相互依赖网络的基本理论，将低阶网络和高阶网络相互依赖，当低阶网络被随机移除1－p的节点后，低阶网络会分裂成多个连通分量，高低阶耦合网络将发生相继故障，直到低阶网络和高阶网络的巨型强连通分量相同时，高低阶耦合网络达到一个稳定的状态，利用稳定时低阶网络的巨型强连通分量的变化情况来研究该高低阶耦合网络的鲁棒性。

2 高低阶耦合网络

本文提出了无向网络的高低阶耦合网络模型。无向三元闭合结构（三个节点的全连接结构）是无向网络的三阶模体，即三阶闭包模体，通过该三阶模体可以构建无向网络的高阶网络模型。低阶网络与高阶网络之间存在依赖关系，通过该依赖关系构建高低阶耦合网络模型。

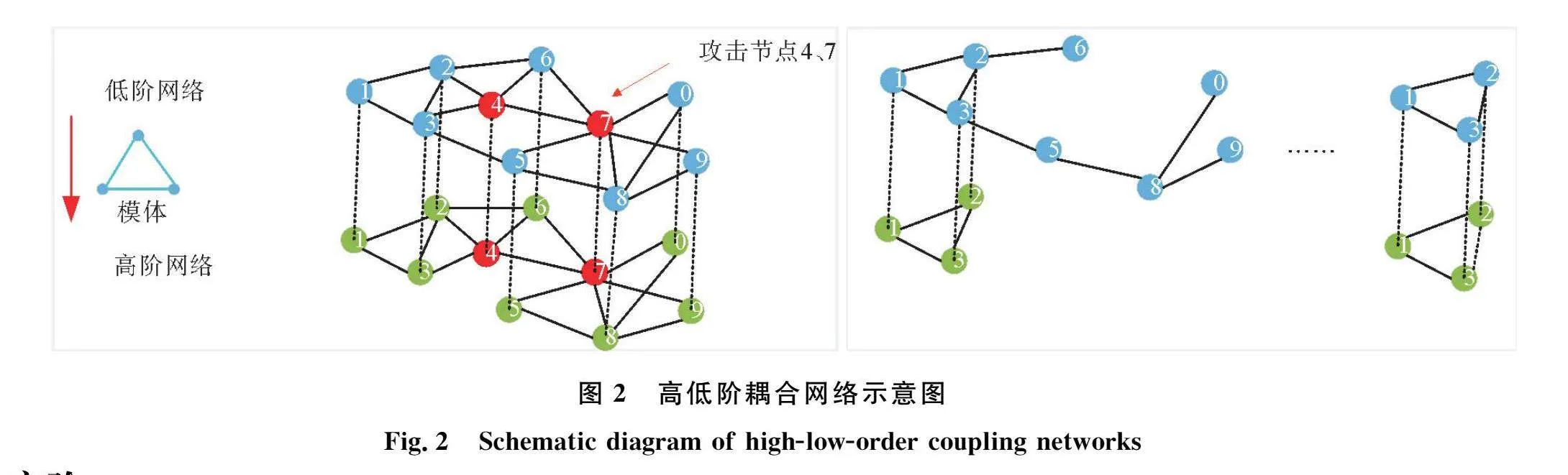
简单起见，新建两个网络A和B，其中网络A是一个独立的无向网络，同时它也是低阶网络。再以无向三元闭合结构作为三阶模体，构建网络A的高阶网络，即网络B。两个网络的节点数相同，并且在网络A和网络B中构建一对一的依赖连边。如图2所示，蓝色无向网络为低阶网络，绿色无向网络为低阶网络的高阶网络。攻击低阶网络中的节点4、7，高阶网络中的节点4、7失效，同时高阶网络中节点4、7所在模体的其他节点0、5、6、8、9也同样失效，高低阶耦合网络发生相继故障后，各自的最大连通子图都只有3个节点。

3 实验

为研究高低阶耦合网络的鲁棒性，本文构建了ER、SW、BA网络的高低阶耦合网络，同时也将高低阶耦合网络模型应用于20个真实网络中，对低阶网络进行随机攻击，研究高低阶耦合网络的鲁棒性，并和其低阶网络的鲁棒性进行对比。

3.1 实验数据集

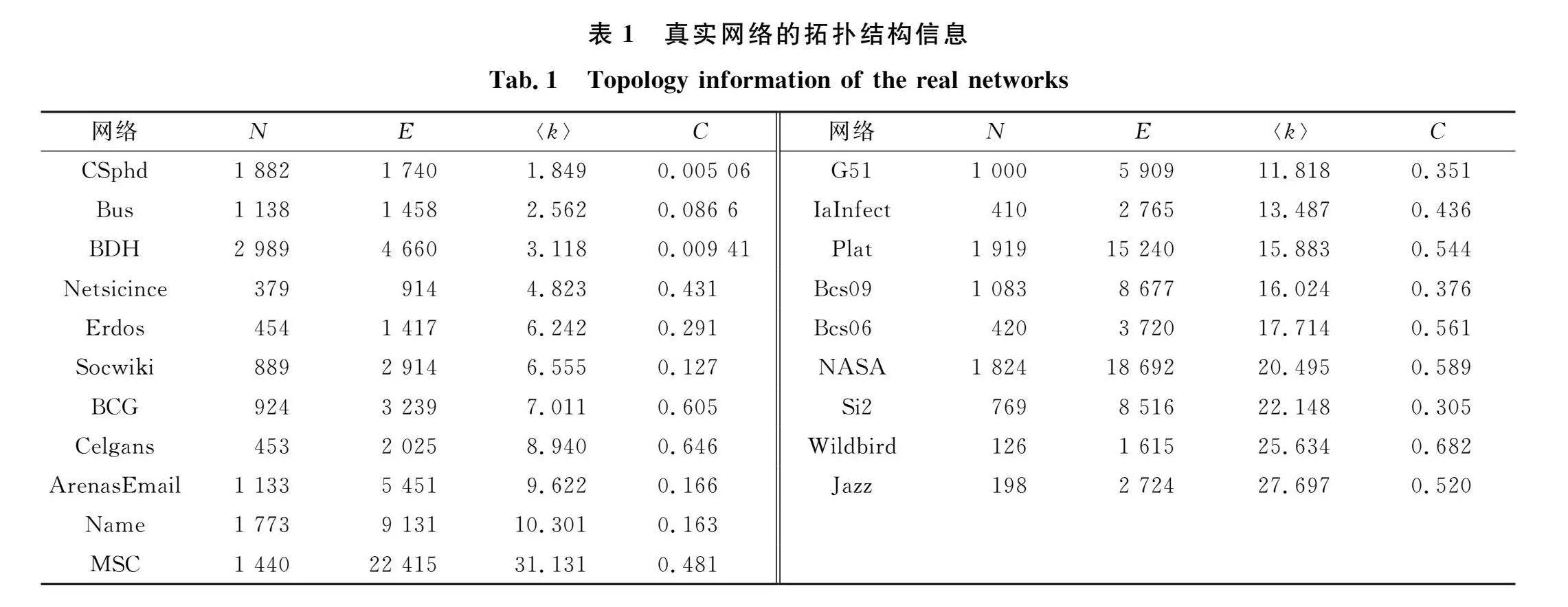
为研究多种场景下高低阶耦合网络的鲁棒性，本文选择了20个不同领域的真实网络数据集，其中包括合作网络（CSphd、Erdos、Netscience、f0d85d7e3a5a0f533dea4291724e71c52439d94a89b827b143db5e96aff043b7Jazz）、电子邮件网络（ArenasEmail）、生物网络（BDH、BCG、Celgans）、杂项网络（Name、G51、Si2、MSC、Plat、NASA）、社交互动网络（Socwiki、IaInfect）、电力网络（Bus、Bcs09、Bcs06）、生态网络（Wildbird），这些数据集全部来自文献[24]。具体的真实网络的基本属性如表1所示。表1中N为网络的节点总数，E为网络连边总数，〈k〉为网络的平均度，C为网络的集聚系数。本文选取的真实网络的平均度范围在 32之间。

3.2 实验结果分析

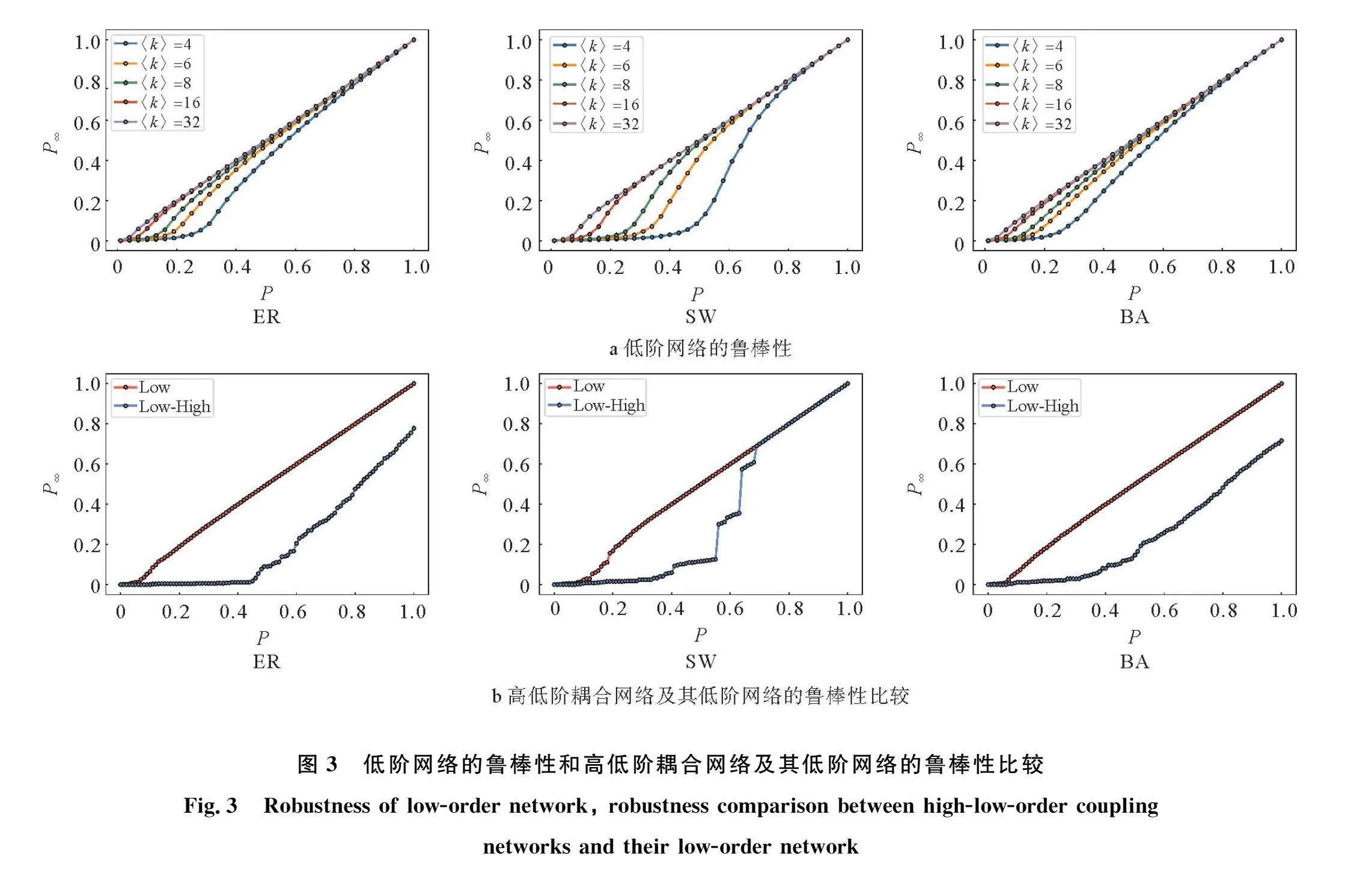
图3展示了低阶网络遭受随机攻击后，低阶网络和其高低阶耦合网络的鲁棒性比较。其中图3中的网络的相关参数为：低阶网络的节点数为1 000，SW网络的断边重连概率为0.05，BA网络的度分布的幂指数为-3，图3b中的低阶网络的平均度〈k〉为16，Low曲线为低阶网络PSymboleB@变化情况，Low-High曲线为高低阶耦合网络的PSymboleB@变化情况。

如图3a所示，当低阶网络的节点数相同时，网络的平均度〈k〉越大，低阶网络的鲁棒性就越强，即低阶网络的鲁棒性与平均度成正比。对于ER、SW、BA网络来说，网络的平均度越大，说明网络中任意两个节点之间的连通路径就越多，即使网络被移除部分节点后，其余节点仍然能够保持良好的连通性，因此平均度大的网络具有较强的鲁棒性。接着，本文生成了节点数为1 000、平均度为16的ER、SW、BA网络，并对它们进行随机攻击，以研究低阶网络和其高低阶耦合网络的鲁棒性，结果如图3b所示。可以发现ER、BA、SW低阶网络的渗流皆为连续相变，BA、ER高低阶耦合网络的渗流同样也是连续相变，而SW高低阶耦合网络的渗流却是不连续相变，这说明SW高低阶耦合网络对于随机攻击比较敏感。ER、BA网络未被攻击时，其高阶网络拥有多个子图分量，因此高低阶耦合网络同样发生相继故障，即当p=1时，高低阶耦合网络的PSymboleB@值不为1。同时从图3b中也可以发现，ER、BA、SW网络的Low曲线均在Low-High曲线的上方，这说明低阶网络PSymboleB@的下降速度比高低阶耦合网络快，这也意味着低阶网络的鲁棒性比高低阶耦合网络强，即高低阶耦合网络比较脆弱。

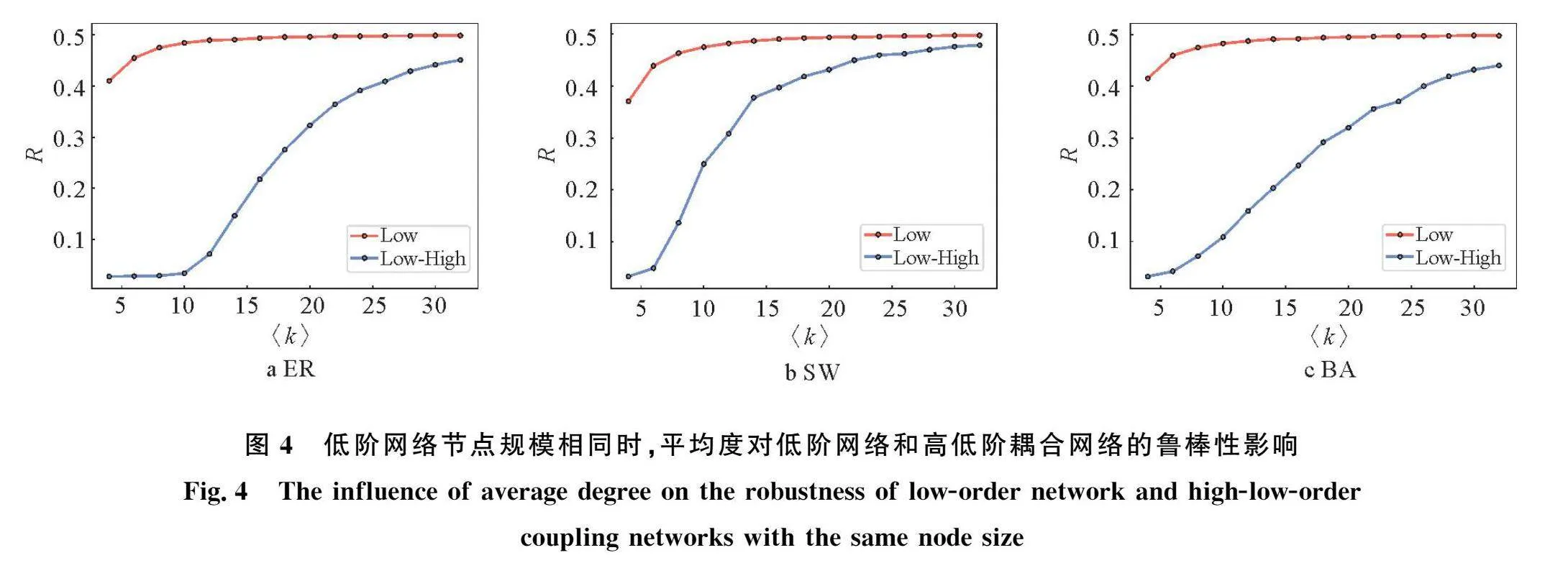
图3b中的低阶网络的节点数和平均度均相同，低阶网络遭受随机攻击后，ER、BA、SW的高低阶耦合网络的鲁棒性都比其低阶网络脆弱。于是本文将ER、BA、SW网络的规模设置为相同的数值，通过调整网络的平均度，研究低阶网络和其高低阶耦合网络的鲁棒性变化。在这一实验中，本文采用了PSymboleB@变化曲线的曲线下面积R来评估网络的鲁棒性，R的值越大，说明网络的鲁棒性越强。相关实验结果如图4所示，图4网络的相关参数：低阶网络的节点数均为1 000，低阶网络的平均度调整范围为〈k〉∈4，6，8，…，32。

如图4所示，低阶网络遭受随机攻击后，无论低阶网络的平均度如何变化，低阶网络的R值均大于高低阶耦合网络的R值，即高低阶耦合网络的鲁棒性比低阶网络差。在低阶网络规模相同的情况下，随着低阶网络平均度的增大，低阶网络的R也在缓慢增大，且低阶网络的R值普遍大于0.4，这说明低阶网络应对随机攻击的能力很强。在无向网络中，网络的平均度越大，则说明网络中的冗余连边多，网络即便被移除部分节点，其余节点仍然有路径连通，导致低阶网络的PSymboleB@的变化曲线接近曲线y=x，即低阶网络的R接近0.5。而对于高低阶耦合网络，低阶网络的平均度越小，高低阶耦合网络的鲁棒性就越脆弱。当低阶网络的平均度小于10时，ER、BA、SW高低阶耦合网络的R均小于0.2，尤其是ER高低阶耦合网络的R几乎等于0，而且与其对应的低阶网络的R相比差异巨大，这些都表明高低阶耦合网络十分脆弱。但是随着低阶网络平均度的增大，高低阶耦合网络的R值也在逐渐上升，高低阶耦合网络的鲁棒性与低阶网络的平均度成正比，同时低阶网络和高低阶耦合网络的鲁棒性差异也在不断减小。

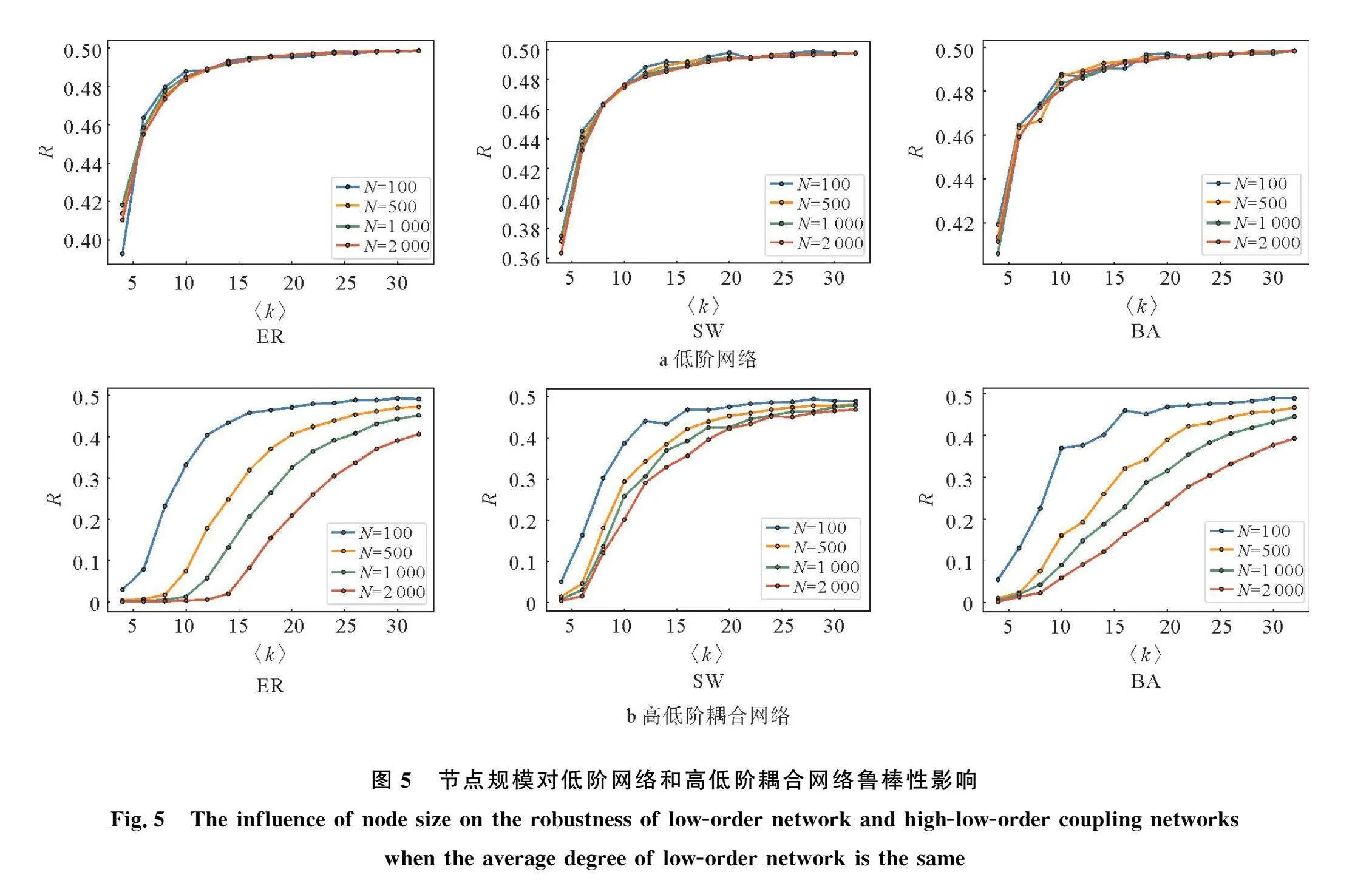
图5展示了当低阶网络规模相同时，低阶网络平均度对高低阶耦合网络的鲁棒性影响，结果表明高低阶耦合网络的鲁棒性与平均度成正比。接着本文将ER、BA、SW网络的平均度设置为定值，通过调整网络的节点规模，研究高低阶耦合网络的鲁棒性。相关实验结果如图5所示，图中网络的相关参数为：低阶网络节点数调整范围为N∈100，500，1 000，2 000，低阶网络的平均度范围为〈k〉∈4，6，…，32。

在图5a中，当低阶网络的平均度相同时，节点数规模N增大，低阶网络的R值几乎没有变化，这说明低阶网络的鲁棒性与节点数规模无关。然而在图5b中，当低阶网络的平均度相同时，随着节点规模N的增大，高低阶耦合网络的R值在逐渐减小，这一现象在ER、BA高低阶耦合网络中尤为明显，这些都表明高低阶耦合网络的鲁棒性与节点规模成反比。

在上述实验中，本文研究了ER、SW、BA网络中低阶网络和高低阶耦合网络的鲁棒性，研究结果表明低阶网络比高低阶耦合网络强健。那么现实中的真实网络是否也存在这样的现象，本文接下来将构建真实网络的高低阶耦合网络模型，并研究它们的鲁棒性。

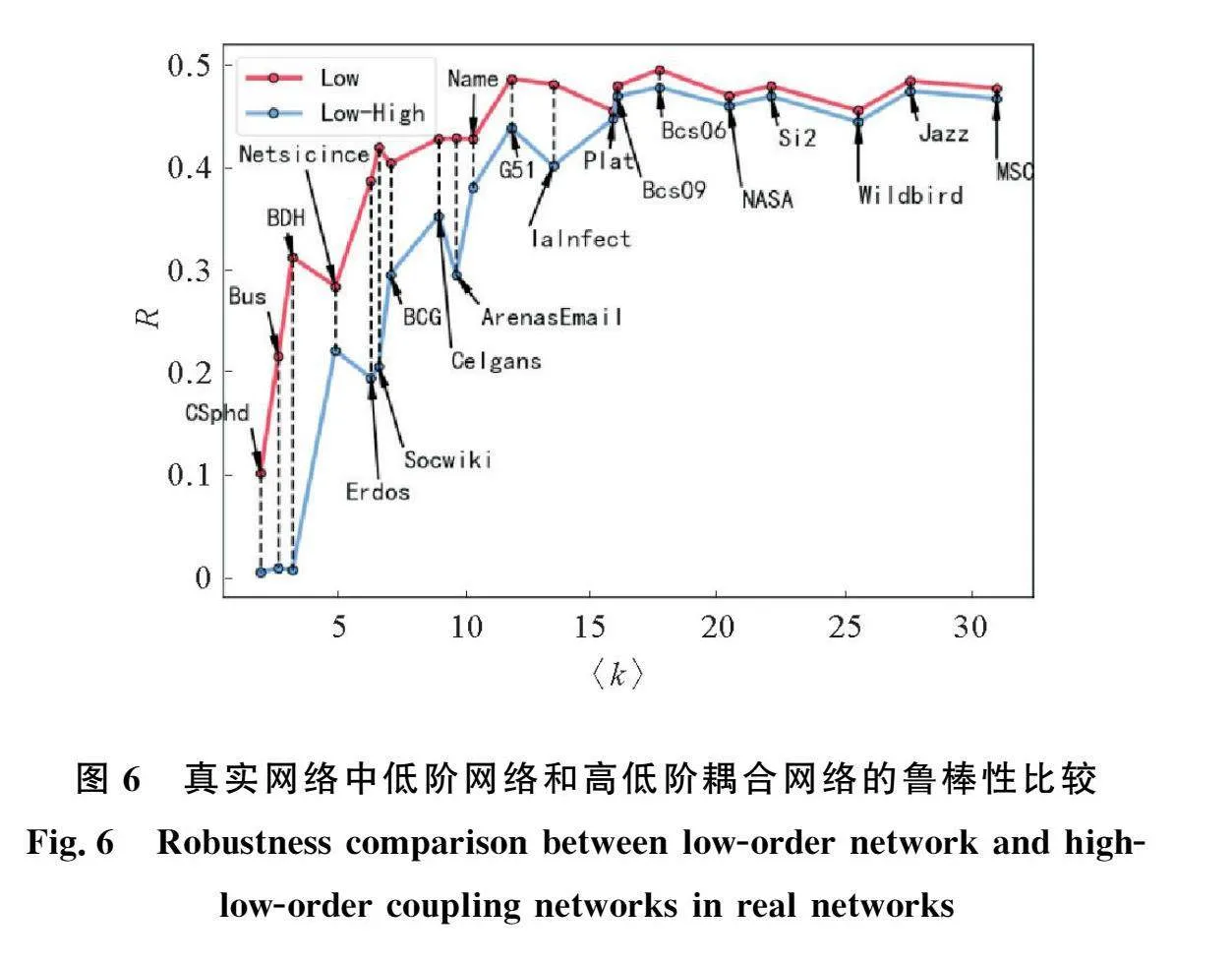
图6展示了不同平均度的真实网络被随机攻击后，其低阶网络和高低阶耦合网络的鲁棒性。这20个真实网络中低阶网络的R值均大于其高低阶耦合网络的R值，这说明这些真实网络的低阶网络鲁棒性要强于其高低阶耦合网络的鲁棒性，即高低阶耦合网络比较脆弱。真实网络的平均度越大，其高低阶耦合网络抵抗随机攻击的能力越强，且与低阶网络的鲁棒性差异也越小。

4 结语

本文提出了一种无向网络的高低阶耦合网络模型，采用随机攻击的方法，对高低阶耦合网络的鲁棒性进行研究。在ER、SW、BA网络中，其低阶网络的鲁棒性要强于高低阶耦合网络，并且高低阶耦合网络的鲁棒性与低阶网络的平均度成正比，与低阶网络的节点规模成反比。同样在20个不同领域的真实网络中，其高低阶耦合网络的鲁棒性也比低阶网络脆弱，平均度越大的真实网络，其高低阶耦合网络的鲁棒性也越强。

综上，在无向网络中，高低阶耦合网络要比低阶网络脆弱，复杂网络会随着低阶网络和高阶网络的相互依赖而变得脆弱。传统网络科学认为复杂网络的鲁棒性与网络节点规模无关，但是本文研究发现当复杂网络中的高低阶网络耦合以后，低阶网络的节点规模越大，高低阶耦合网络的鲁棒性就越差，这个结论与传统复杂网络鲁棒性研究的结论完全不一致，该结论也对未来的网络鲁棒性研究具有了一定的指导意义。

参考文献：

[1]NICOL D M， YAN G. High-performance simulation of low-resolution network flows[J]. Simulation， 2006， 82（1）： 2142.

[2]WERNER N E， BUMPUS M F， ROCK D. Involvement in internet aggression during early adolescence[J]. J Youth Adolesc， 2010， 39（6）： 607619.

[3]BABA T， MATSUDA S. Tracing network attacks to their sources[J]. IEEE Internet Computing， 2002， 6（2）： 2026.

[4]ERDS P， RNYI A. On random graphs[J]. Publicationes Mathematicae Debrecen， 1959， 6： 290297.

[5]ERDS P， RNYI A. On the evolution of random graphs[J]. Publications of the Mathematical Institute of the Hungarian Academy of Sciences， 1960， 5（1）： 1760.

[6]PRICE D. Networks of scientific papers[J]. Science， 1965， 149（3683）： 510515.

[7]PRICE D. A general theory of bibliometric and other cumulative advantage processes[J]. Journal of the American Society for Information Science， 1976， 27（5）： 292306.

[8]WATTS D J， STROGATZ S H. Collective dynamics of "small-world" networks[J]. Nature， 1998， 393（6684）： 440442.

[9]BARABSI A， ALBERT R. Emergence of scaling in random networks[J]. Science， 1999， 286（5439）： 509512.

[10] ALBERT R， JEONG H， BARABSI A. Error and attack tolerance of complex networks[J]. Nature， 2000， 406（6794）： 378382.

[11] COHEN R， EREZ K， BEN-AVRAHAM D， HAVLIN S. Resilience of the internet to random breakdowns[J]. Physical Review Letters， 2000， 85（21）： 46264628.

[12] COHEN R， EREZ K， BEN-AVRAHAM D， et al. Breakdown of the internet under intentional attack[J]. Physical Review Letters， 200 86（16）： 3682.

[13] FRUTOS B E， MART N R A. Study of the structural and robustness characteristics of madrid metro network[J]. Sustainability， 2019， 11（12）： 3486.

[14] BULDYREV S V， PARSHANI R， PAUL G， et al. Catastrophic cascade of failures in interdependent networks[J]. Nature， 2010， 464（7291）： 10251028.

[15] PARSHANI R， BULDYREV S V， HAVLIN S. Interdependent networks： reducing the coupling strength leads to a change from a first to second order percolation transition[J]. Physical Review Letters， 2010， 105（4）： 048701.

[16] PARSHANI R， BULDYREV S V， HAVLIN S. Critical effect of dependency groups on the function of networks[J]. Proceedings of the National Academy of Sciences， 201 108（3）： 10071010.

[17] RADICCHI F. Percolation in real interdependent networks[J]. Nature Physics， 2015， 11（7）： 597602.

[18] SUN S， WU Y， MA Y， et al. Impact of degree heterogeneity on attack vulnerability of interdependent networks[J]. Scientific Reports， 2016， 6： 32983.

[19] BAI Y N， HUANG N， WANG L， et al. Robustn39eb0f3d76d0dd829fd076480f9975848f5f736e5045e1b4a15ca1847be14ad5ess and vulnerability of networks with dynamical dependency groups[J]. Scientific Reports， 2016， 6： 37749.

[20] SMOLYAK A， LEVY O， VODENSKA I， et al. Mitigation of cascading failures in complex networks[J]. Scientific Reports， 2020， 10（1）： 16124.

[21] TURALSKA M， SWAMI A. Greedy control of cascading failures in interdependent networks[J]. Scientific Reports， 202 11（1）： 110.

[22] BENSON A R， GLEICH D F， LESKOVEC J. Higher-order organization of complex networks[J]. Science， 2016， 353（6295）： 163166.

[23] YIN H， BENSON A R， LESKOVEC J， et al. Local higher-order graph clustering[DB/OL].[20220915].https：//dl.acm.org/doi/proceedings/10.1145/3097983.

[24] ROSSI R， AHMED N. The network data repository with interactive graph analytics and visualization[DB/OL].[20220915].https：//dl.acm.org/doi/10.5555/28881162888372.

（责任编辑 耿金花）