基于TOPSIS的配电网结构优化及关键节点线路识别

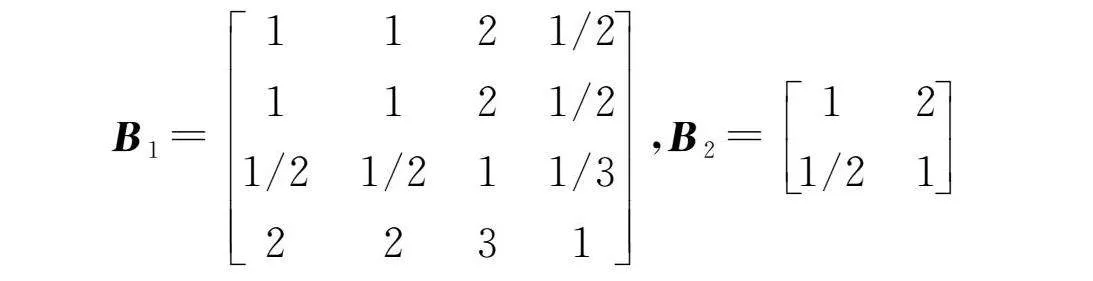
摘要： 为获取较优的配电网拓扑结构并识别网络关键节点和线路，提出一种综合多属性的配电网结构优化和关键节点线路识别方法。首先利用支路交换法获取多个配电网拓扑图，然后基于复杂网络理论构造抗毁性指标，接着采用改进的TOPSIS法找出最优网络，最后构造重要性指标识别关键节点和线路。以IEEE33和PG&E69节点系统为例，对网络做随机攻击，验证优化后的配电网具有更强的抗攻击能力；对配电网采取随机攻击和蓄意攻击，结果表明，在蓄意攻击中，网络的各项指标下降更加显著，证明本方法能够有效识别出关键节点和线路。

关键词： TOPSIS法；支路交换法；复杂网络；结构优化；关键节点线路

中图分类号： TM715;TM711文献标识码： A

Optimization of Distribution Network Structure and Identification of Key Nodes and Lines Based on TOPSIS Method

LIN Siyu， WEN Juan， QU Xing， XIAO Qiankang

（School of Electrical Engineering， University of South China， Hengyang 421000， China）

Abstract：To obtain a better topology and identify the key nodes and lines of distribution networks， this paper presents a multi-attribute method for optimizing network structure and identifya758ea20f6225e52c3077c649f4ca457ing key nodes and lines. Firstly， multiple distribution network topologies are obtained by the branch-exchange algorithm. Secondly， the invulnerability indices are constructed based on complex network theory. Then， the improved TOPSIS method is used to find the optimal network. Finally， the importance indices are constructed to identify key nodes and lines. Taking the 33-bus and 69-bus systems as examples， it verified that the optimized distribution network has stronger anti-attack ability through random attack. Random attacks and deliberate attacks are used on the distribution network. The results show that the network parameters significantly decrease under deliberate attacks， which proves that this method can effectively identify the key nodes and lines.

Keywords： TOPSIS method; branch-exchange algorithm; complex network; structure optimization; key nodes and lines

0 引言

配电网作为连接电力系统和用户之间的纽带，其安全稳定运行对电力系统的可靠性和用户的生产生活都极为重要。随着配电网规模不断扩大，其网络结构复杂性也逐渐增强，当系统中处于核心位置的节点或线路出现问题或受到扰动时，都可能导致大规模的连锁故障，出现大停电事故［1］。因此对配电网进行优化设计［2］，并准确识别网络中的关键节点和线路［34］，对预防配电网大规模级联故障有着重要意义。

目前，配电网结构优化方法通常分为3种［5］：1）提高配电网中各元件的可靠性［67］；2）加入分布式电源，增加供电线路，提升系统的冗余度［8］；3）改变配电网线路中的分段开关及联络开关的开合，调整网络的拓扑结构［910］。方法1）和2）都需要增加投资，方法3）可以利用现有网络的潜在能力提升供电可靠性。因此，在没有足够投资的情况下，可以通过调整配电网拓扑结构达到优化网络的目的［1112］。文献［11］利用支路交换寻优法找出抗毁性最高的网络拓扑结构，但其仅考虑了等效最短路径数；文献［12］采用抗毁性指标作为配电网优化的目标函数，但其仅考虑了线路指标，未充分考虑到网络整体的抗毁性。优化配电网结构后，需要识别网络中的关键节点和线路，目前对配电网关键节点和线路的识别，大多是基于复杂网络理论提出的［1317］。文献［13］利用度值、介数、凝聚度等指标，对节点重要性进行评估，但未对网络中的线路进行分析；文献［14］提出节点度数、节点介数的同时，加入了线路度数、线路介数等概念，但其仅用层次分析法给指标赋予主观权重，未充分考虑到指标数据自身所携带的信息。

综上所述，现有的配电网结构优化和关键节点线路识别方法，或仅用单一指标来寻优，没有从多角度进行分析；或仅考虑节点特性，未对网络整体结构进行分析。为此，本文基于支路交换法实现不同场景下配电网拓扑结构，利用复杂网络理论中的接近中心性、线路度数、网络效率和特征路径长度作为网络结构抗毁性指标，运用层次分析法和熵权法［15］从主客观两个方面设定指标权重，获得抗毁性综合评价指标，在此基础上，采用多属性决策的综合理想排序（Technique for Order Preference by Similarity to Ideal Solution， TOPSIS）［16］与灰色关联度相结合的评价方法对各网络结构抗毁度进行排序，找出最优的配电网拓扑结构。最后构造节点和线路重要性指标，并实现对节点和线路重要度排序。该方法可以获得抗毁性较高的配电网结构，并从多角度对配电网节点和线路进行评价，克服了单一指标在评价时的不足和赋权的主观性，有助于实现对多个不同拓扑结构的配电网进行抗毁性分析。

1 评估指标选取

考虑到配电网闭环设计、开环运行，且网络中存在大量的联络开关和分段开关，结构复杂多样。在构建配电网拓扑结构模型时，需要将系统中的电源节点、负荷节点和传输节点看作拓扑网络中的节点；节点与节点之间的线路看成拓扑网络中的边，节点和边不存在权重。因此，配电网可以简化为一个无自环的无向无权网络G=（V，E），其中V={v v2，…，vN}和E={e e2，…，em}分别为节点和边的集合。

1.1 配电网抗毁性指标

考虑到配电网抗毁性指标需要对网络整体结构进行评价，选取网络效率和特征路径长度作为主要评估指标；从节点和线路角度出发，选取节点接近中心性的平均值和线路度数的平均值作为网络抗毁性的补充指标［17］，其中线路度数的定义为线路连边的个数［14］。各指标公式如表1所示。

1.2 节点和线路重要性指标

选取度中心性、接近中心性、节点介数中心性和凝聚度对节点重要性进行评估。度中心性从局部角度判断该节点与其他节点联系的紧密程度；接近中心性和介数中心性从全局角度判断该节点位于网络中心性的程度；凝聚度通过对节点收缩后网络凝聚度的变化，从全局和局部两个角度反映该节点的重要程度［1819］。选取线路介数和线路度数对线路重要性进行评估。线路介数和线路度数两个指标分别从全局和局部两个角度反映该线路在网络中的重要程度［14］。各指标公式如表1所示。

2 配电网优化及评估模型构建

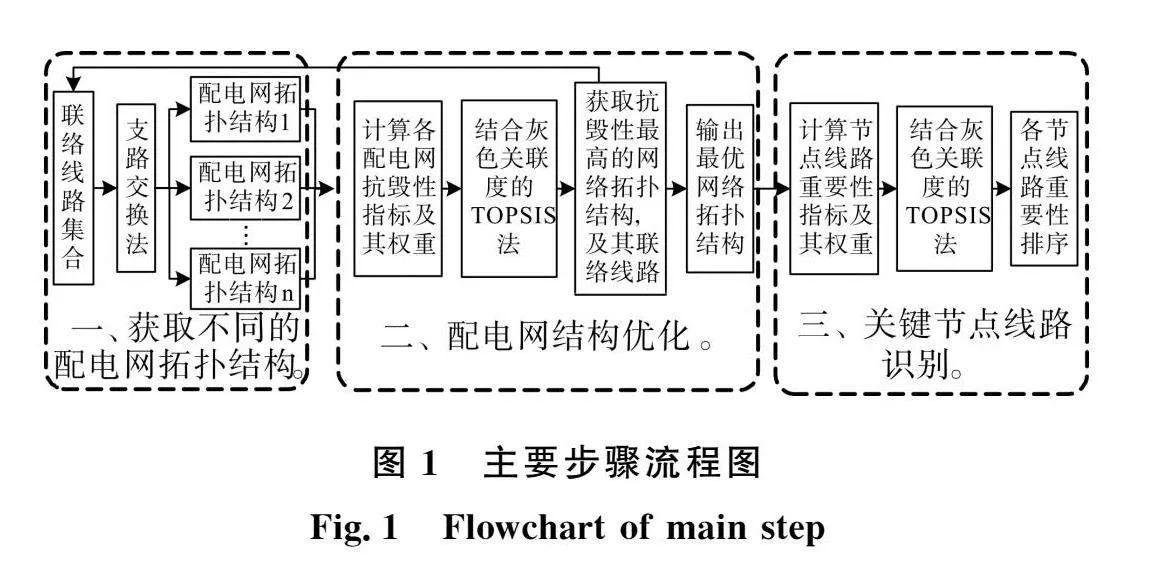
配电网拓扑结构优化及关键节点线路识别模型包括3部分：1）基于支路交换法，根据不同的联络线路集合获取多个配电网拓扑结构；2）利用TOPSIS法识别抗毁性最高的网络拓扑结构，多次迭代获取最优网络拓扑结构，3）再次利用TOPSIS法识别最优网络的关键节点和线路。其主要步骤流程如图1所示。本节详细介绍各步骤的实现。

2.1 基于支路交换法的配电网优化模型

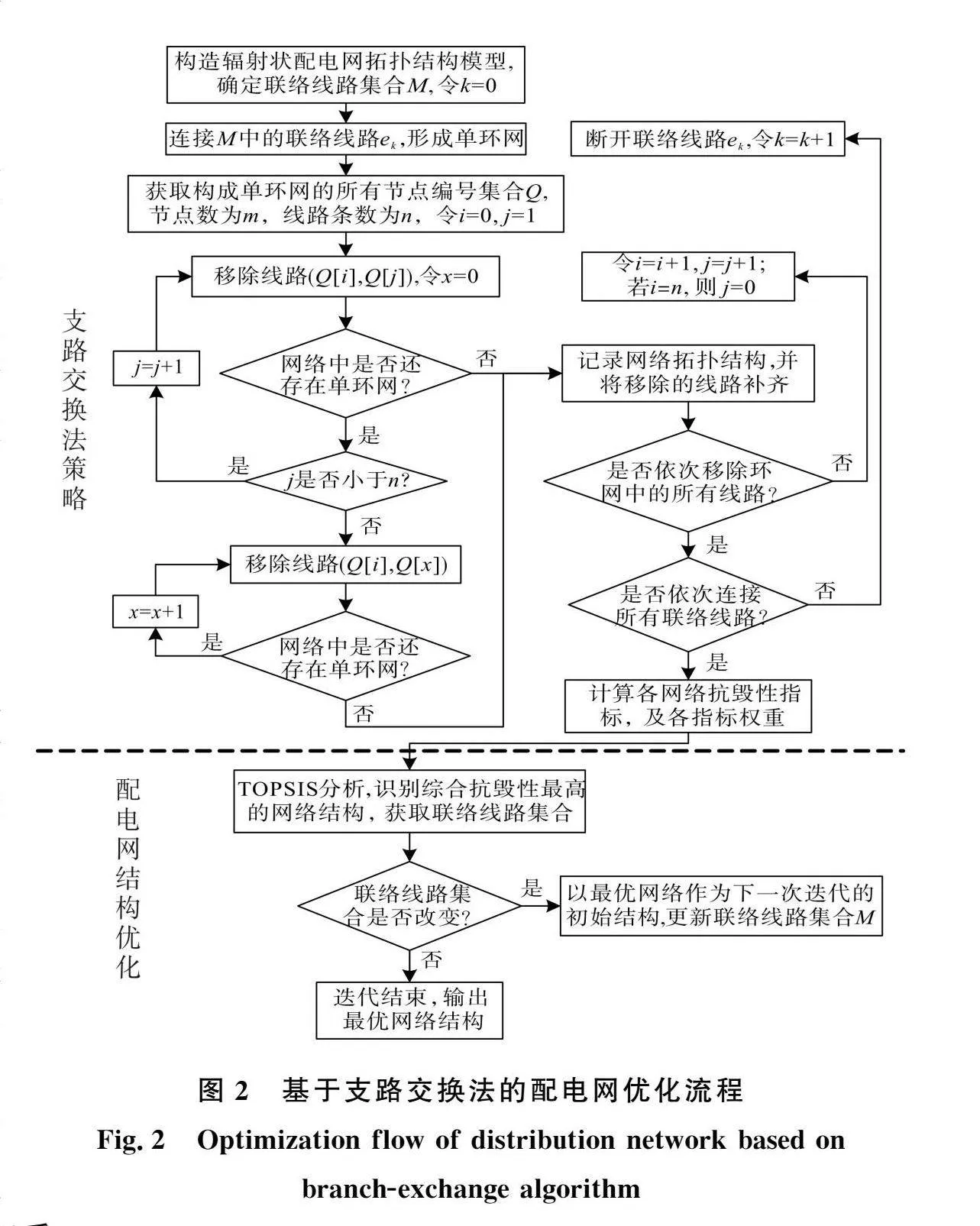
本文利用Python中的NetworkX库实现多个配电网拓扑结构，采用TOPSIS法识别综合抗毁性最高的网络，通过判断联络开关集合是否改变，决定是否进入下一次迭代，多次迭代得到最优网络结构。该模型采用minimum_cycle_basis（G）函数获取单环网中所有节点集合，利用节点集遍历单环网中的所有线路，依次断开不同线路获取不同配电网结构。具体流程如图2所示，其中ek代表第k条联络线路，（Q［i］，Q［j］）、（Q［i］，Q［x］）代表以节点集Q组成的线路。

2.2 综合权重设置

为了保证赋权的公正性，使得结果不完全依赖人的主观判断且能反映评价指标参数中携带的客观信息，本文采用层次分析法和熵权法从主客观两个角度对各项指标进行赋权。

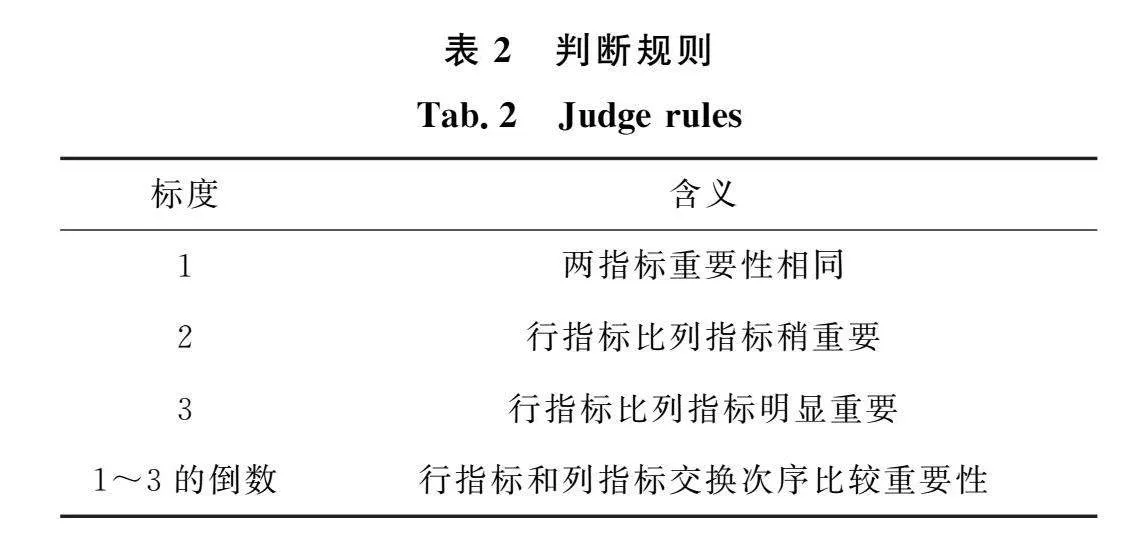
层次分析法将人们对各个指标的认识定量化，通过构造比较矩阵来计算各指标的权重。其计算过程为［20］：首先根据各指标的定义，将评估指标采用三层标度来表示各指标的重要程度，对指标进行两两对比得到标度矩阵R=［rij］m×m，其判断规则见表2；然后采用文献［20］的方法，将标度矩阵进行无量纲化处理变换为判别矩阵，经过一致性检验后得到各指标主观权重ε1j。

熵权法作为一种客观权重的计算方法，直接利用各项指标参数信息得到指标权重。其基本原理是根据指标变异量的大小来确定权重，若某个指标取值的差异性越大，其蕴涵的信息量就越多，在综合评价中所能起的作用越大，其权重也就越大。计算过程为：

首先，将数据标准化为效益型指标。然后将标准化后的数值按yij=xij/∑mi=1xij求得各指标在各方案下的比值yij，其中xij为标准化后的数值，m为各指标种类数。接着，通过式（1）求出各指标的信息熵ej。

ej=1ln（m）∑mi=1yijln（yij）（1）

最后，通过式（2）求得各指标的客观权重ε2j。

ε2j=1-ejm-∑mj=1ej，（j=，…，m）（2）

综合主观权重和客观权重的计算结果，代入式（3）可以得到指标的综合权重εj。

εj= ε1jε2j∑mj=1 ε1jε2j，（j=，…，m）（3）

2.3 结合灰色关联度的TOPSIS法评估模型

TOPSIS法是求解多属性决策问题中常用且十分有效的一种方法，其核心思想是选取各指标的正负理想解，然后以此为基准度量某个解靠近正理想解和远离负理想解的程度，并依次对各方案进行排序。虽然TOPSIS法对原始数据的利用十分充分，但实验获取的信息数据依然具有局限性，于是引入灰色关联度这一指标来弥补信息量的不足。其具体流程：

1）根据支路交换法获取的配电网拓扑结构模型，计算各网络的抗毁性指标参数，以网络结构为行向量，抗毁性指标为列向量，设网络个数为n，指标个数为m，构造评价矩阵X=（xij）n×m。

2）对评价矩阵中的各元素进行标准化处理，得到标准化评价矩阵R=（rij）n×m，其中rij=xij/ ∑ni=1x2ij，对各评价指标j设置权重系数W=（ωj）1×m（j=，…，m），得到各指标下的加权决策矩阵Z=（zij）n×m=（ωjrij）n×m。

3）确定各指标下的正理想方案Z+和负理想方案Z-，其中Z+j=max{Zij}1≤i≤n，Z-j=min{Zij}1≤i≤n，j=，…，m。

4）根据式（4）计算各评价方案与正、负理想方案的欧氏距离。

M+i= ∑mj=1（Z+j-Zij）2M-i= ∑mj=1（Z-j-Zij）2（4）

5）基于加权决策矩阵，计算各方案与理想方案的灰色关联度，与正理想方案的灰色关联系数矩阵为U+=（u+ij）n×m，与负理想方案的灰色关联系数矩阵为U-=（u-ij）n×m。其中

u+ij=miniminj|Z+j-Zij|+0.5maximaxj|Z+j-Zij||Z+j-Zij|+0.5maximaxj|Z+j-Zij|u-ij=miniminj|Z-j-Zij|+0.5maximaxj|Z-j-Zij||Z-j-Zij|+0.5maximaxj|Z-j-Zij|（5）

根据灰色关联系数矩阵，得到各方案与正负理想方案的灰色关联度分别为N+i=1m∑mj=1u+ij、N-i=1m∑mj=1u-ij。

6）分别对欧氏距离M+i、M-i和灰色关联度N+i、N-i做标准化处理，进而可以得到各方案与正、负理想方案的贴近距离：L+i=αM-i+βN+i，L-i=αM+i+βN-i，其中α和β分别表示各方案与正理想方案在位置和形状上的接近程度系数，满足α+β=1，本文认为欧氏距离和灰色关联度同等重要，均取为0.5。

7）计算各方案的相对贴近度：

Di=L+i/（L+i+L-i）（6）

贴进度可以用来衡量该配电网结构抗毁性与最优解的相近程度，根据相对贴近度的大小可以对不同结构配电网的抗毁性进行排序，贴进度越大则该网络的抗毁性越好。

8）通过支路交换法结合TOPSIS法对配电网拓扑结构进行优化后，计算优化后配电网节点和线路重要性指标参数，设节点个数为n′，线路条数为n″，对应的指标个数为m′和m″，分别以节点和线路作为行向量，以评价指标作为列向量，构造评价矩阵X′=（x′ij）n′×m′和X″=（x″ij）n″×m″，重复步骤2）～7），即可获得节点和线路的重要性排序。

3 算例分析

本文利用Jupyter Notebook软件进行仿真分析，选择IEEE33节点系统［14］和PG&E69节点系统［22］作为案例，构建拓扑结构模型，通过NetworkX库计算结构抗毁性指标和节点线路重要性指标。

3.1 配电网结构优化

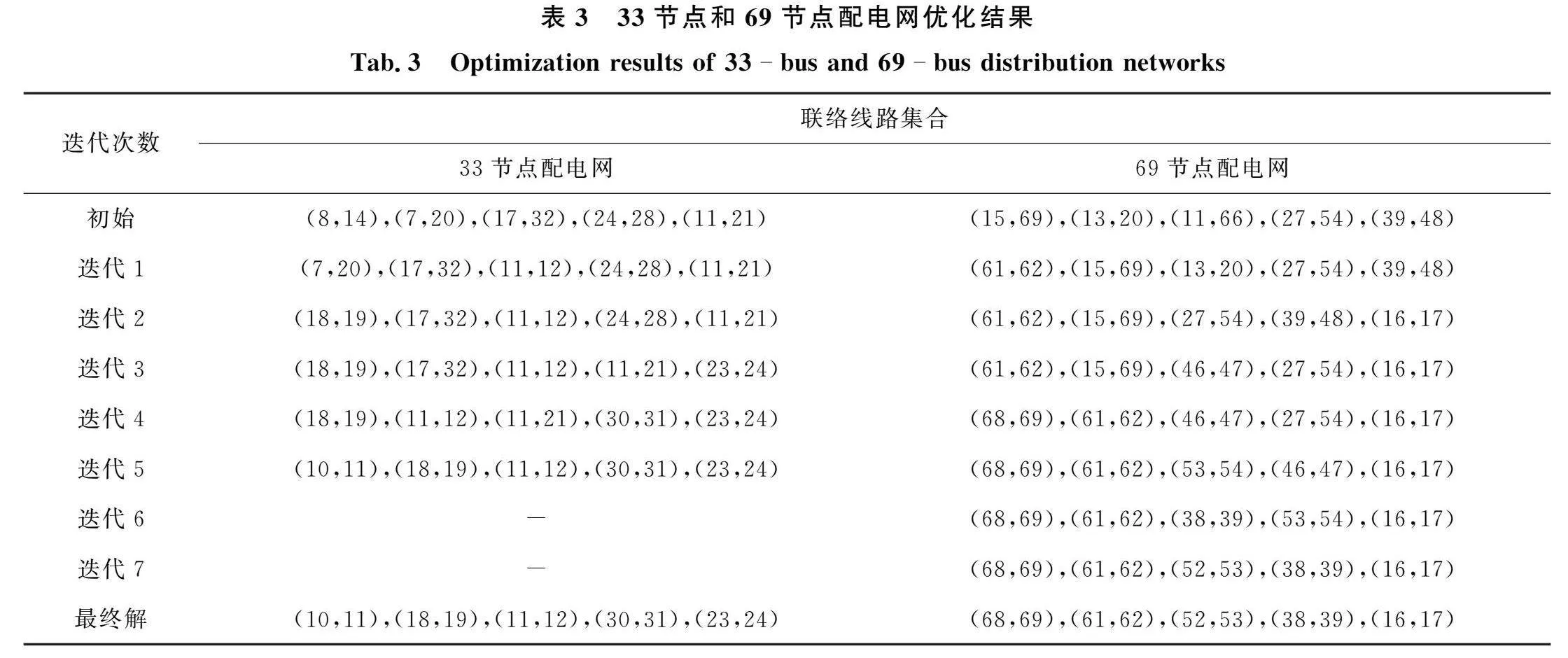
本文基于支路交换法获取不同拓扑结构的配电网模型，通过熵权法和层次分析法组合赋权构造抗毁性综合评估指标，采用TOPSIS法结合灰色关联度对网络结构进行排序，以排名第一的网络作为下一次迭代的初始网络，IEEE33节点网络迭代5次后收敛，PG&E69节点网络迭代7次后收敛，每次迭代断开的线路集合如表3所示。

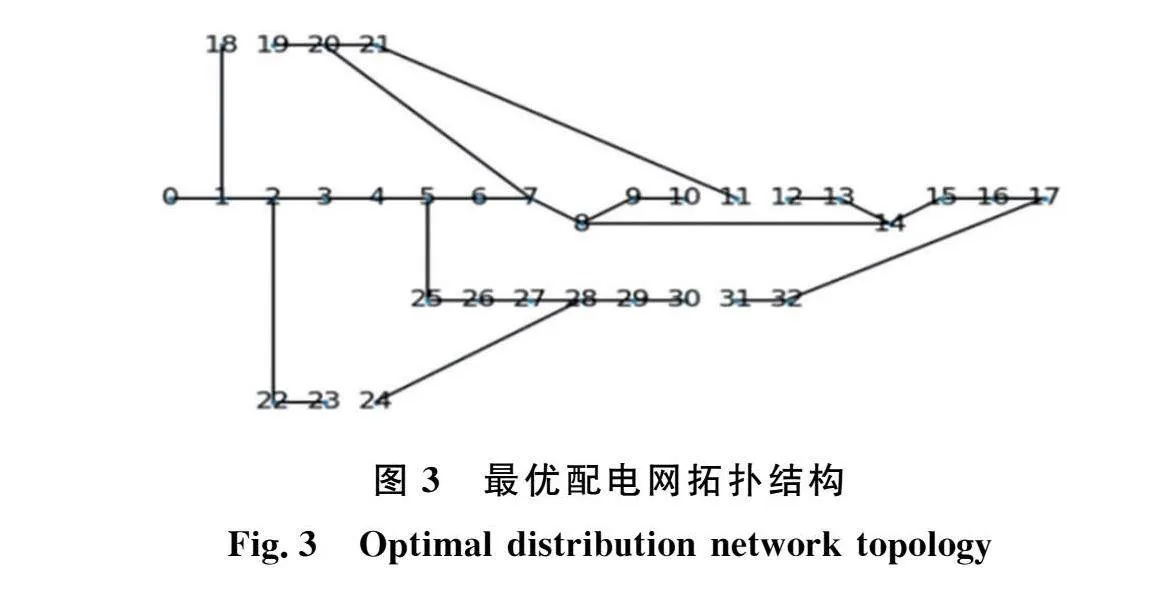
由表3可知，每次迭代的联络线路集合都会改变，随着迭代次数增多，联络线路集合趋于稳定，在第5次迭代后，33节点配电网联络线路集合不再发生变化，此时得到的最优配电网如图3所示。文献［11］采用多场景、多目标抗毁性优化模型，以抗毁性最强和切负荷最小为目标对33节点配电网进行优化，得到如图4所示配电网。

与文献［11］对比，两种方法都断开了（10，11）、（1 12）这两条线路，其他3条断开的线路略有差别。文献［11］以网络抗毁度最高为目标，并以网络线损作为补充，最终迭代7次得到最优配电网；本文以联络线路集合不再变化作为迭代结束标准，最终迭代5次获得最优配电网，因此从算法的迭代次数上看，本文方法更有优势。

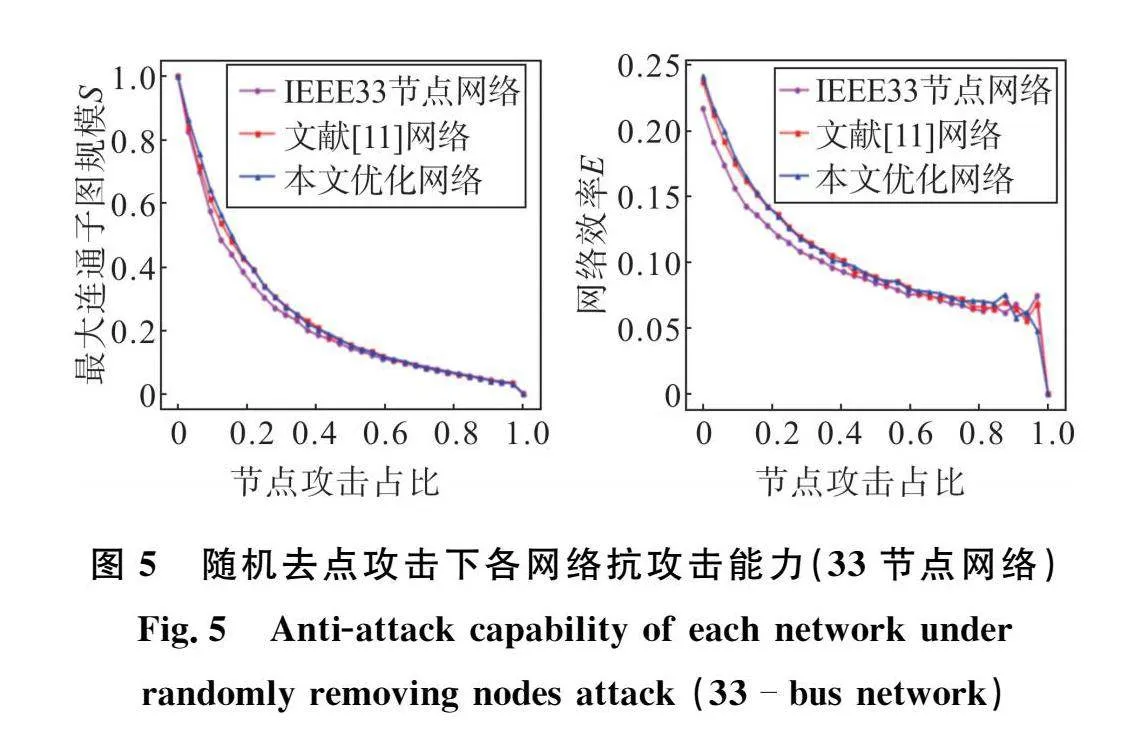
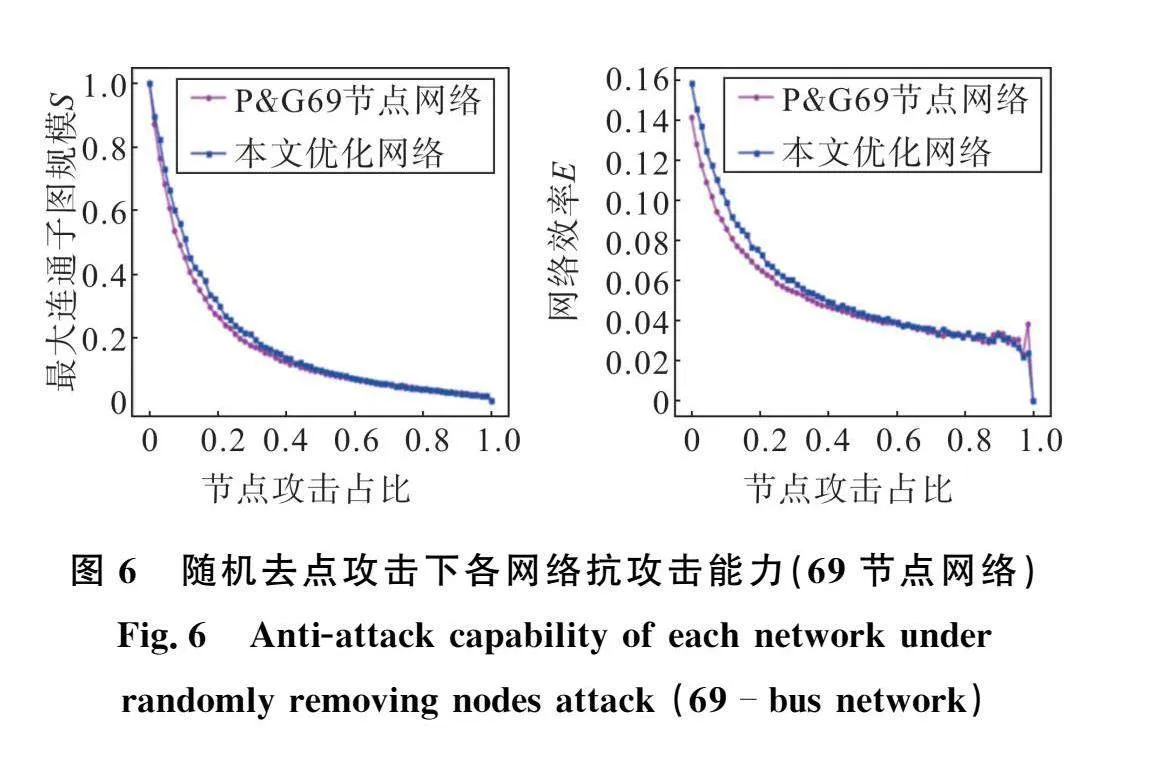
为了验证所得最优配电网的有效性，对本文优化的33节点配电网、文献［11］配电网和IEEE33节点配电网［14］做随机去点攻击［22］，分析实施攻击后网络的最大连通子图规模S和网络效率E两个指标参数变化，以此判断配电网抵抗随机攻击的能力，结果如图5所示。对本文优化的69节点配电网和PG&E69节点配电网做随机攻击分析，结果如图6所示。

正常运行时，令各网络最大连通子图规模S都为1，IEEE33节点网络、文献［11］网络和本文优化后的33节点网络的初始网络效率E计算结果分别为0.216 2、0.237 0和0.241 3，PG&E69节点网络和本文优化后的69节点网络的初始网络效率E计算结果分别为0.141 4和0.158 6。在前3次攻击下，IEEE33节点网络、文献［11］网络和本文优化后的33节点网络的S值分别降低了40.95%、36.48%和34.44%，E值分别降低了27.20%、24.35%和24.91%，PG&E69节点网络和本文优化后的69节点网络的S值分别降低了31.31%和27.37%，E值分别降低了16.62%和14.40%。对数据分析可知，本文优化后的网络初始网络效率更高5e92432d03060416832ea5ab13218d322629486320cf235e0fb859a5833efe7c，且在受到攻击时，各指标下降程度更低，因此抵抗随机攻击的能力更强。从图5和图6中各指标下降曲线可知，随着攻击次数增多，经典网络各指标下降更快，而本文优化后的两个网络和文献［11］网络下降幅度相近且较慢，因此可以证明本文优化方法的有效性。

3.2 配电网关键节点线路识别

对3.1节获得的最优配电网进行分析，运用层次分析法计算各指标的主观权重。根据1.2节中各指标衡量不同节点和不同线路重要性的差别。在节点评估中，认为凝聚度指标最重要，接近中心性指标和介数中心性指标次之，度中心性指标重要性最低。在线路评估中，认为线路介数指标的重要性高于线路度数。因此，基于以上判断和表2的赋值规则构造比较矩阵B1和B2：

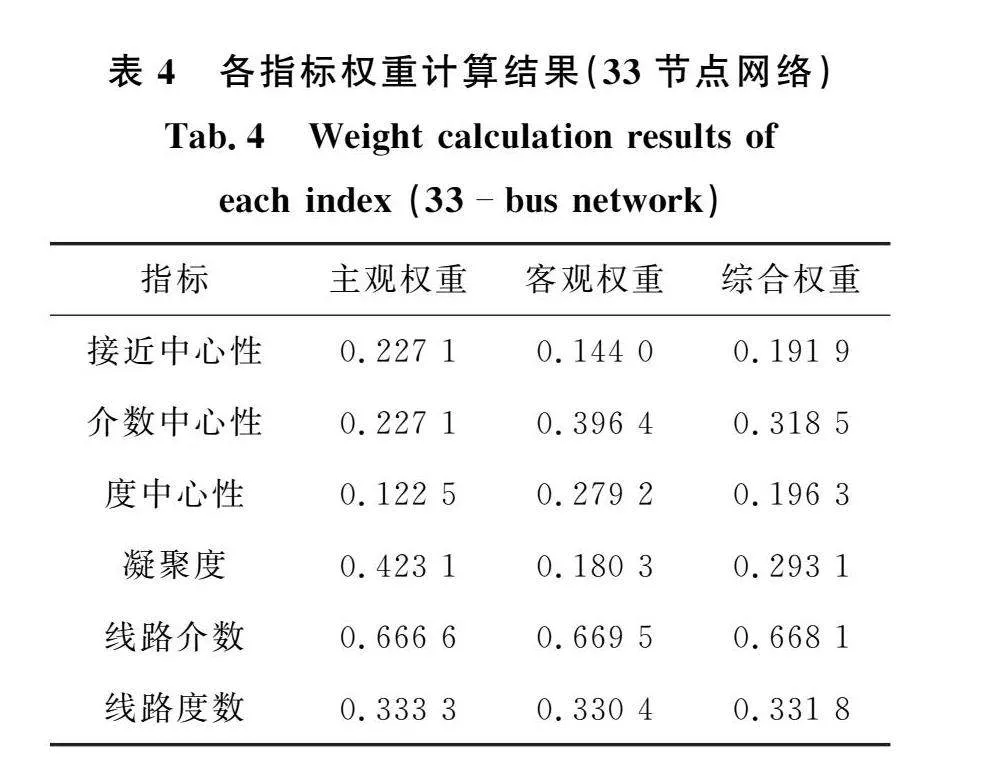
根据比较矩阵B1和B2，构造判别矩阵并进行一致性检验。结合熵权法得到的各指标的客观权重，利用式（3）综合主客观权重，得到33节点网络的各指标权重信息如表4所示：

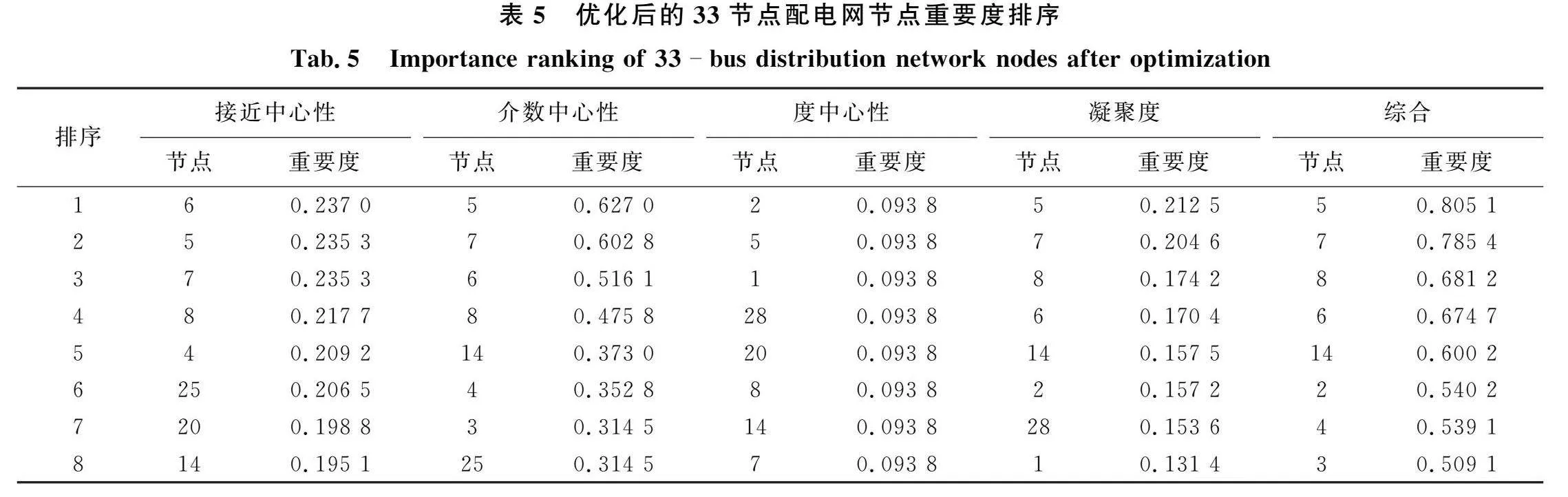
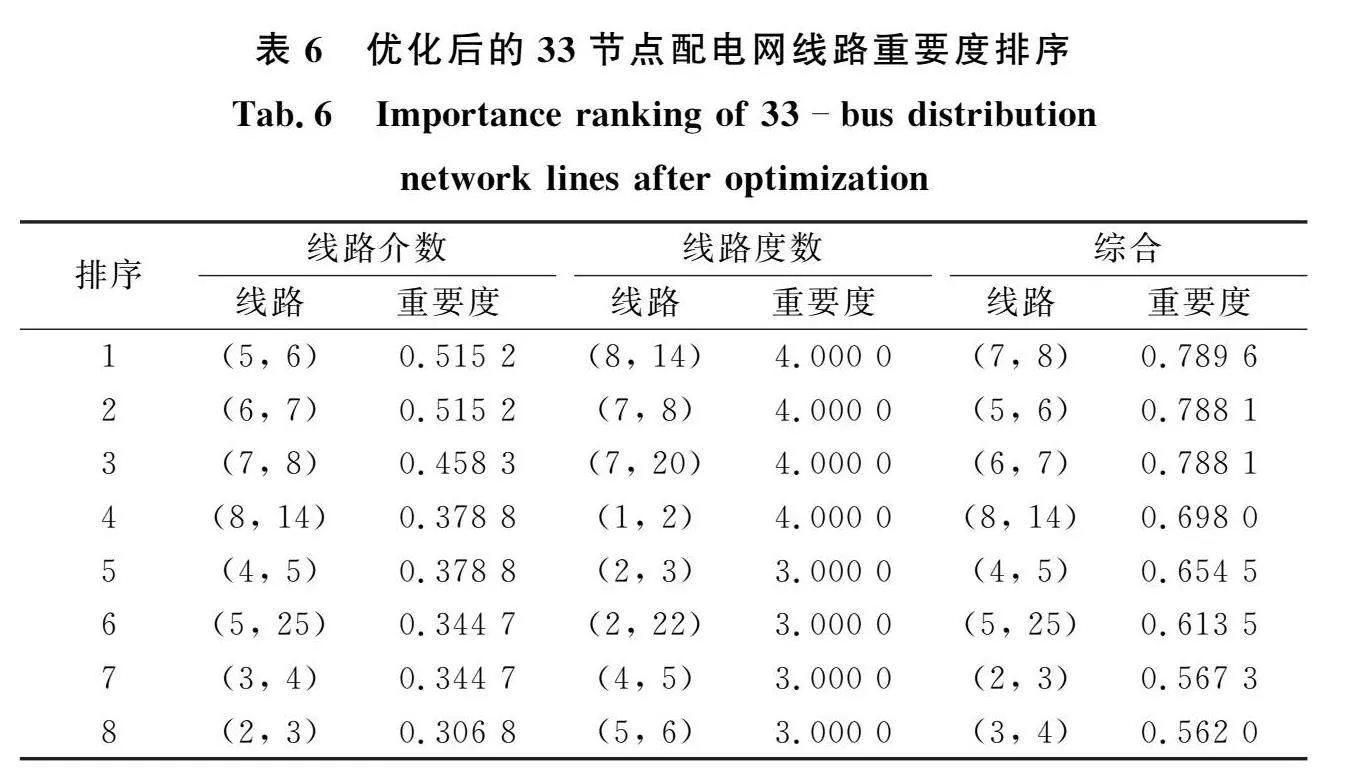
从表4可知，在节点的客观权重中，介数中心性权重最大，这是由于配电网为辐射状网络，拥有多个度为1的叶子节点，这类节点的介数中心性为0，因此介数中心性指标各数值相差较大；在线路各指标权重中，主观和客观权重相差不大，符合定性分析的结果。根据各指标参数及其对应的权重，利用2.3节的方法得到优化后的33节点和69节点配电网节点和线路重要度排序结果。因篇幅原因，这里列出33节点配电网排序前8的节点和线路，结果如表5和表6所示。

由表5和表6可知，节点和线路各指标的独立排序结果和综合排序结果不尽相同，这是因为每个指标都是从单一角度描述节点和线路的重要性，其评价结果有一定的局限性，而综合各指标后的排序结果考虑了指标间的互补性，更加具有说服力。

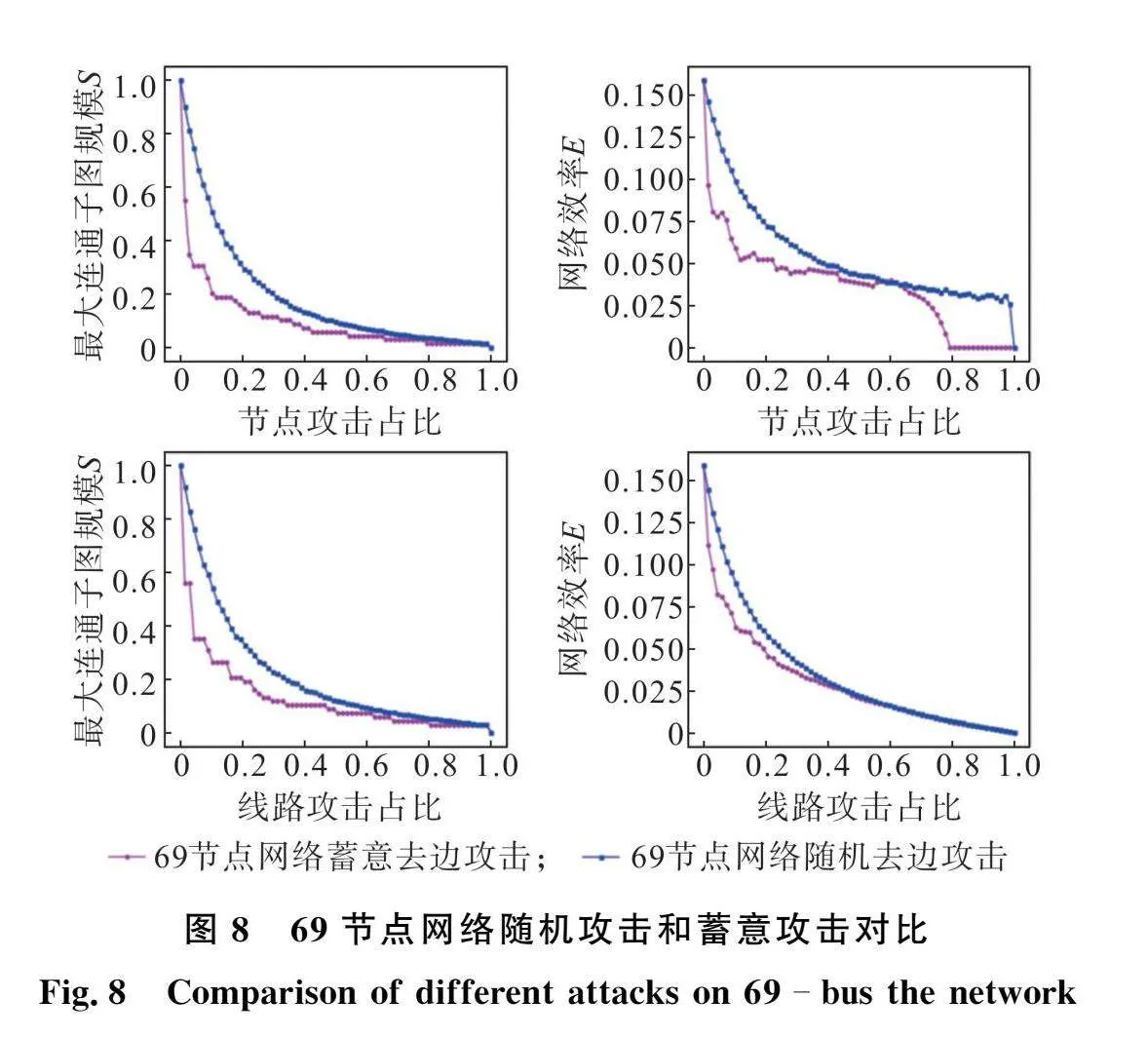
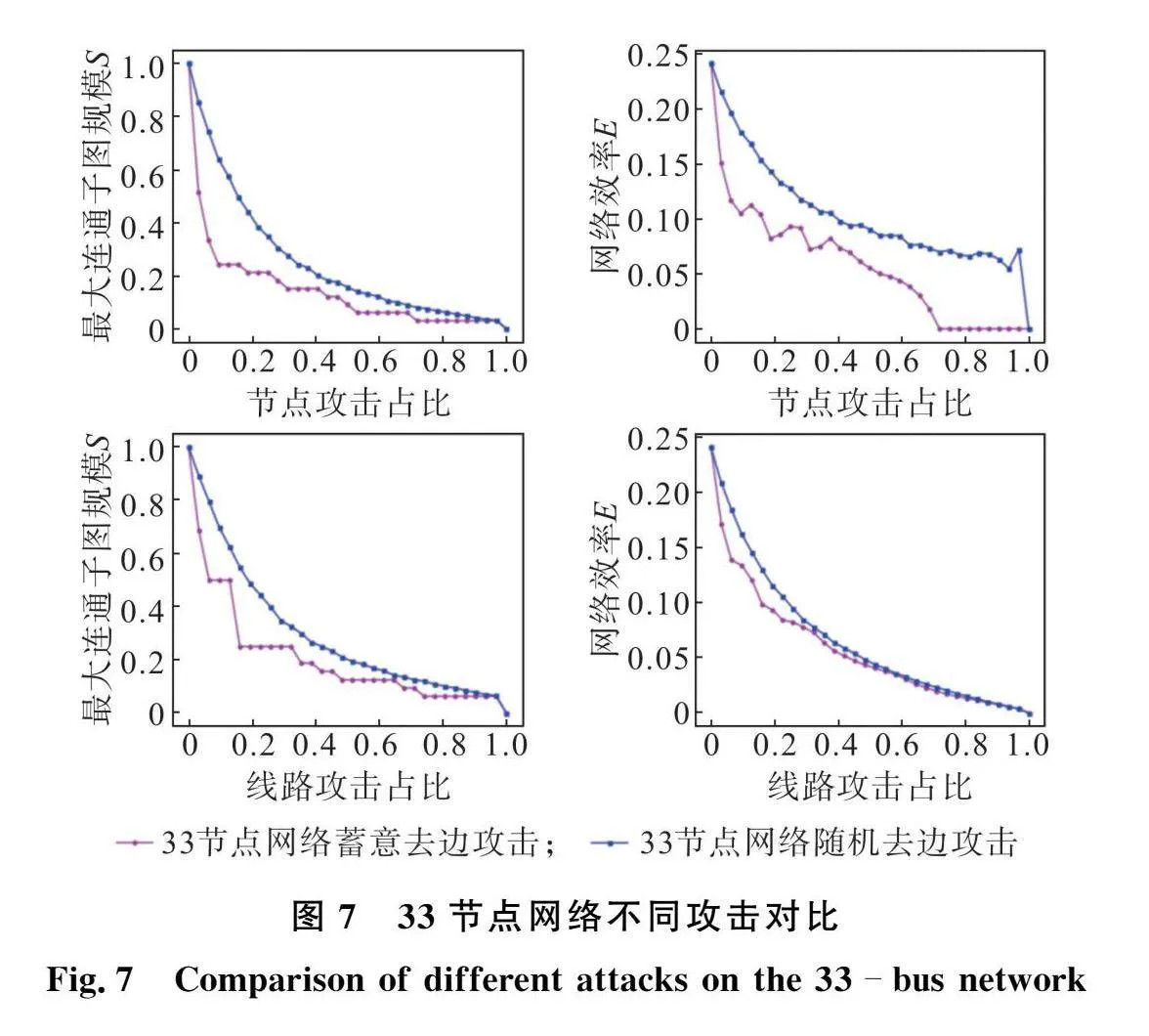
为了验证本方法识别关键节点和线路的正确性，对配电网拓扑结构进行两种攻击策略，即随机（去点、去边）攻击和蓄意（去点、去边）攻击［22］，蓄意攻击策略是依次移除重要度较高的节点和线路。通过对比移除不同比例的节点和线路后网络的最大连通子图规模S和网络效率E的变化，来验证关键节点和线路识别的正确性，结果如图7和图8所示。

在移除3个关键节点后，33节点网络的S值和E值分别下降了75.76%、56.55%，移除3条重要线路后，网络的S值和E值分别下降了50%、44.41%；而随机移除3个节点，两指标仅下降36.27%、25.65%，随机移除3条线路，两指标仅下降29.71%、32.25%。同样，在移除69节点网络的关键环节后，网络的S值和E值下降幅度更大。由图7和图8可知，相比于随机攻击，蓄意攻击使得网络各项指标下降更快，表明配电网关键环节受到攻击后所带来的危害更大，证明本文识别出的关键节点和线路是有效可信的。

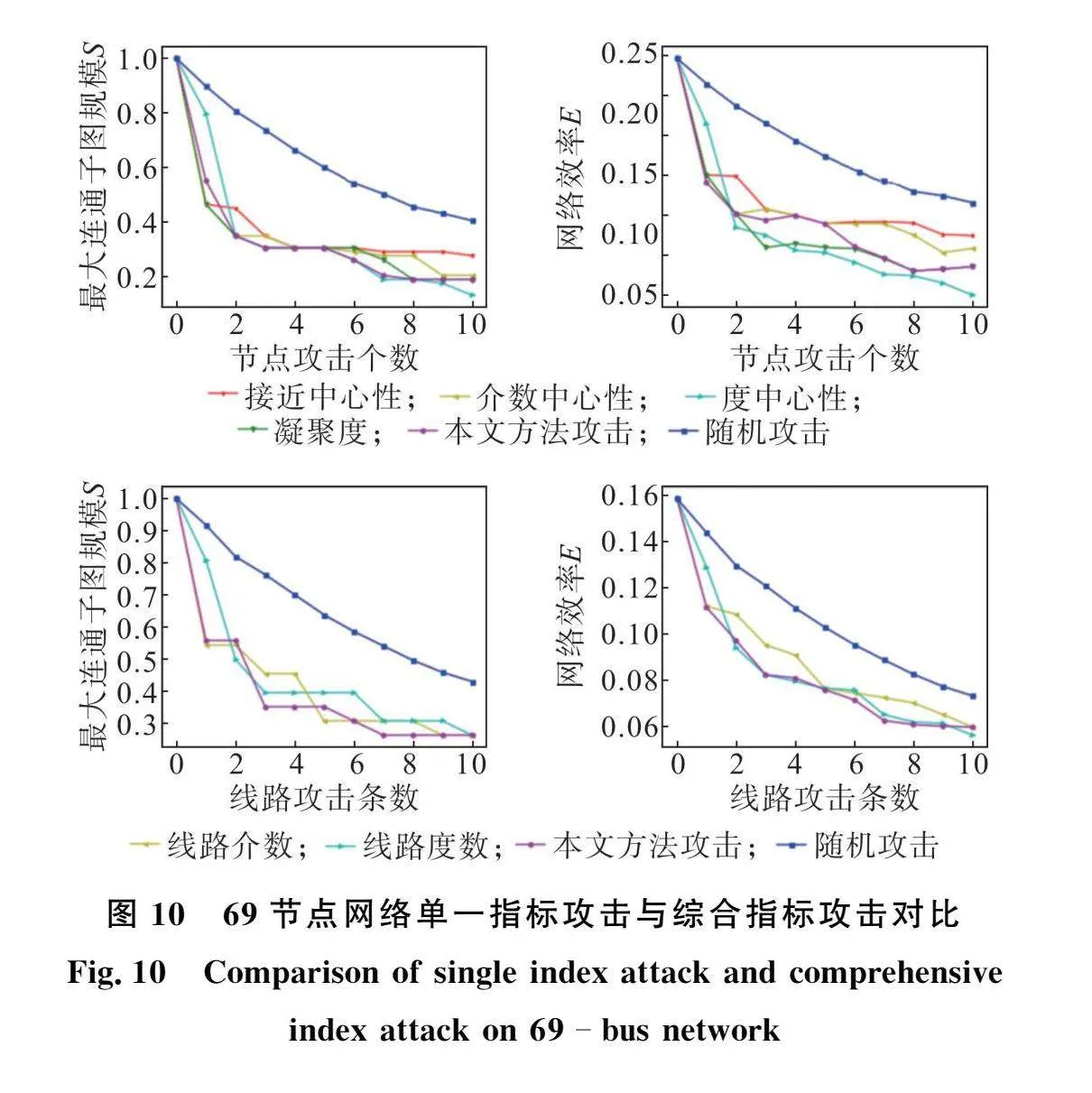
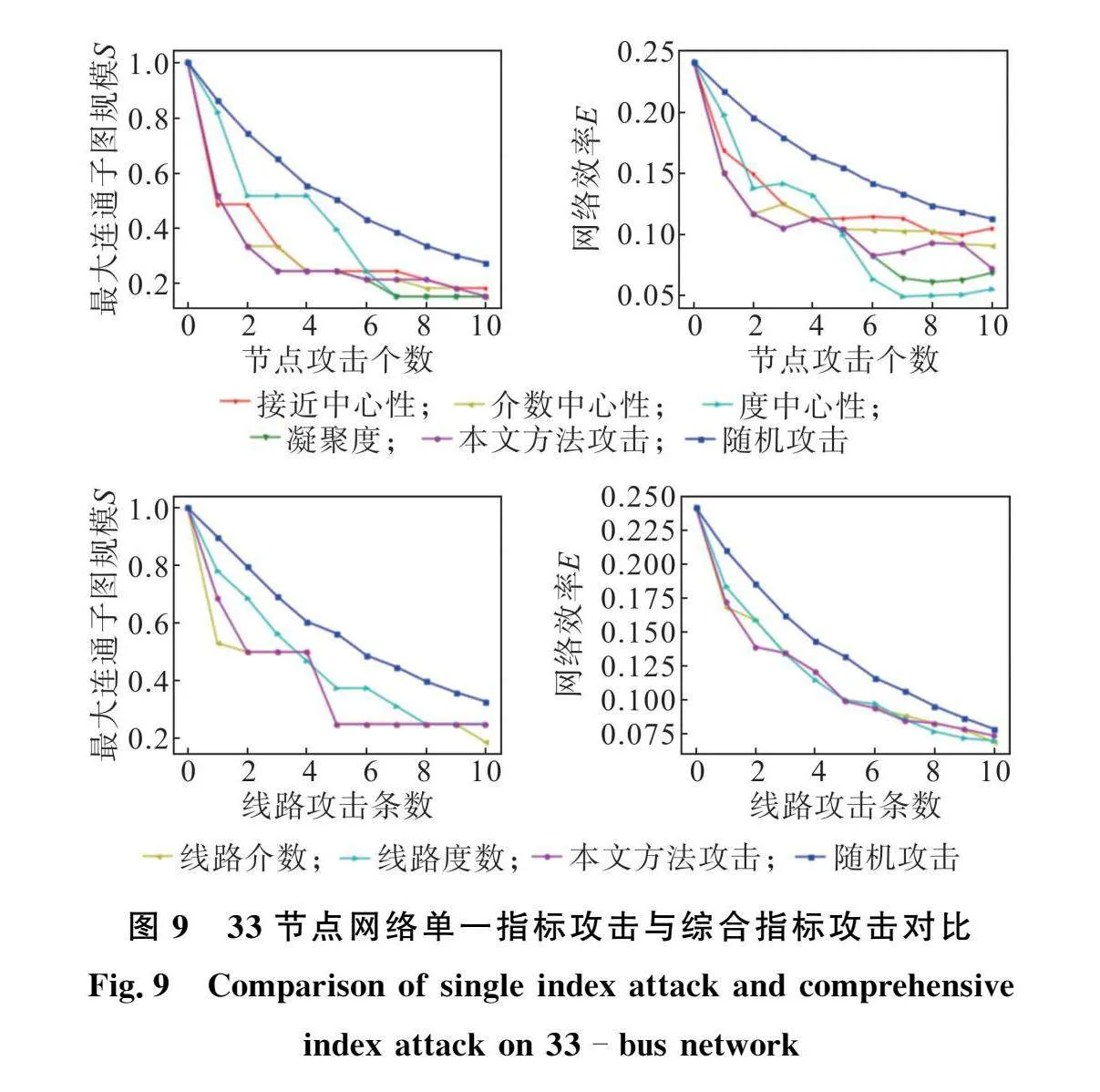
同时，本文将单一指标攻击与综合指标攻击结果做对比，依次攻击33节点和69节点配电网中重要度较高的前10个节点和前10条线路，获得的结果如图9和图10所示。

从图9中可以看出，在前5个节点和线路被攻击后，网络的各项指标参数出现大幅下降，随着网络中被攻击节点和线路数量的增加，网络的各项指标下降逐渐平缓，这说明配电网对关键节点和线路的依赖性远大于普通节点和线路。与单一指标攻击相比，按综合指标攻击节点和线路后，网络的最大连通子图规模和网络效率下降更为显著，这是由于单一指标仅考虑网络某一方面的特性，而综合指标将各单一指标特性进行互补，进一步说明考虑多指标的必要性。图10对69节点网络的攻击结果分析与图9基本一致。

4 结论

本文提出了基于支路交换法的配电网优化模型，该模型利用TOPSIS法将多个抗毁性指标进行综合，弥补了单一指标的不足，并且能同时对多个配电网进行分析，可以为多个配电网拓扑结构优劣评比提供参考。以IEEE33和PG&E69节点系统为例，对配电网进行随机（去点、去边）攻击和蓄意（去点、去边）攻击。结果表明，相比于随机攻击节点和线路，在攻击关键节点和线路后，配电网最大连通子图规模和网络效率都发生了大幅下降，证明本方法识别出关键节点和线路的有效性。随着智能配电网的不断发展和大量分布式电源的接入，配电网的规模逐渐增大且电气特性趋于复杂，如何对更大规模配电网进行建模并对接入分布式电源的配电网节点和线路重要性指标进行定义，将是下一步研究的重点。

参考文献：

［1］胡源， 薛松， 张寒， 等. 近30年全球大停电事故发生的深层次原因分析及启示［J］. 中国电力， 202 54（10）： 204210.

HU Y， XUE S， ZHANG H， et al. Analysis and enlightenment of global power failure in recent 30 years ［J］. Electric Power， 202 54（10）： 204210.

［2］LIAO H L. Review on distribution network optimization under uncertainty ［J］. Energies， 2019， 12（17）： 121.

［3］GENG J Q， Sun X M， LI F， et al. Prediction method of important nodes and transmission lines in power system transactive management ［J］. Electric Power Systems Research， 2022， 208： 18.

［4］ALIREZA S， MOHAMMAD K， ALI M， Vulnerability analysis of power grid with the network science approach based on actual grid characteristics： a case study in Iran ［J］. Physica A： Statistical Mechanics and Its Applications， 2019， 513： 1421.

［5］董政呈， 方彦军， 田猛. 相互依存网络抗毁性研究综述［J］. 复杂系统与复杂性科学， 2017， 14（3）： 3044.

DONG Z C， FANG Y J， TIAN M. Review on invulnerability of interdependent networks ［J］. Complex System and Complexity Science， 2017， 14（3）： 3044.

［6］LI H C， LI B， LUO Z G， et al. Power supply reliability enhancement for low-voltage distribution area with power quality improvement function ［J］. IEEE Access， 2022， 10： 130619130631.

［7］WANG C， ZHANG T Y， LUO F Z， et al. Fault incidence matrix based reliability evaluation method for complex distribution system ［J］. IEEE Transactions on Power Systems， 2018， 33（6）： 67366745.

［8］潘本仁， 王和春， 张妍， 等. 含分布式电源的主动配电网重构策略研究［J］. 电力系统保护与控制， 2020， 48（15）： 102107.

PAN B R， WANG H C， ZHANG Y， et al. Study on an active distribution network reconstruction strategy with distributed power supply ［J］. Power System Protection and Control， 2020， 48（15）： 102107.

［9］于艾清， 丁丽青， 王育飞， 等. 基于单环寻优策略的有源配网重构方法［J］. 电力系统保护与控制， 2022， 50（1）： 2332.

YU A Q， DING L Q， WANG Y F， et al. Active distribution network reconfiguration based on single loop optimization strategy ［J］. Power System Protection and Control， 2022， 50（1）： 2332.

［10］ SILVA L I， BELATI E A， GEREZ C， et al. Reduced search space combined with particle swarm optimization for distribution system reconfiguration ［J］. Electrical Engineering， 202 103（2）： 11271139.

［11］ 李珂， 王金凤， 杨丽徙， 等. 基于多场景抗毁性分析的配电网网络结构优化［J］. 电力系统自动化， 2014， 38 （1）： 3438.

LI K， WANG J F， YANG L X， et al. Coordination between load shedding for safety and stability control and under-frequency load shedding in a small weak receiving power system ［J］. Automation of Electric Power System， 2014， 38（1）： 3438.

［12］ 李奔， 刘会家， 李珺. 考虑网络结构优化的含风电配电网多目标重构［J］. 电力系统保护与控制， 2015， 43（17）： 5762.

LI B， LIU H J， LI J. Multiobjective reconfiguration of distribution network with wind power generators considering network survivability ［J］. Power System Protection and Control， 2015， 43（17）： 5762.

［13］ 吴辉， 彭敏放， 张海艳， 等.基于复杂网络理论的配电网节点脆弱度评估［J］.复杂系统与复杂性科学， 2017， 14（1）： 3845.

WU H， PENG M F， ZHANG H Y， et al. Node vulnerability assessment for distribution network based on complex network theory ［J］. Complex System and Complexity Science， 2017， 14（1）： 3845.

［14］ 史文超， 李晓明， 王孝琳， 等. 配电网脆弱性评估方法［J］. 电力系统及其自动化学报， 2018， 30（12）： 125131.

SHI W C， LI X M， WANG X L， et al. Vulnerability assessment method for distribution network ［J］. Proceedings of the CSU-EPSA， 2018， 30（12）： 125131.

［15］ WANG T， DU Z A， ZHANG K J， et al. Reliability evaluation of high voltage direct current transmission protection system based on interval analytic hierarchy process and interval entropy method mixed weighting ［J］. Energy Reports， 202 7： 9099.

［16］ BAI S S， ZHANG Y K， LI L J， et al. Effective link prediction in multiplex networks： a TOPSIS method ［J］， Expert Systems with Applications， 202 177： 116.

［17］ WANG L， LIN K， ZHANG W， et al. Invulnerability analysis of power distribution network based on topology structure ［C］. 2019 6th International Conference on Systems and Informatics （ICSAI）. Shanghai， 2019： 330334.

［18］ 王梓行， 姜大立， 漆磊， 等. 基于冗余度的复杂网络抗毁性及节点重要度评估模型［J］. 复杂系统与复杂性科学， 2020， 17（3）： 7885.

WANG Z H， JIANG D L， QI L， et al. Complex network invulnerability and node importance evaluation model based on redundancy ［J］. Complex System and Complexity Science， 2020， 17（3）： 7885.

［19］ MENG Y Y， TIAN X L， LI Z W， et al. Exploring node importance evolution of weighted complex networks in urban rail transit ［J］. Physica A： Statistical Mechanics and Its Applications， 2020， 558： 115.

［20］ 何铭， 邹艳丽， 梁明月， 等. 基于多属性决策的电力网络关键节点识别［J］. 复杂系统与复杂性科学， 2020， 17（3）： 2737.

HE M， ZOU Y L， LIANG M Y， et al. Critical node identification of a power grid based on multi-attribute decision ［J］. Complex System and Complexity Science， 2020， 17（3）： 2737.

［21］ WEN J， QU X， LIN S Y， et al. An optimization method of active distribution network considering time variations in load and renewable distributed generation ［J］. International Transactions on Electrical Energy Systems， 2022， 2022：121.

［22］ FU C Q， WANG Y， Wang X Y， et al. Multi-node attack strategy of complex networks due to cascading breakdown ［J］. Chaos， Solitons & Fractals， 2018， 106： 6166.

（责任编辑 李 进）