基于社团结构的抑制校园新冠传播研究

摘要： 校园是一个特殊的人群密集场所，如果校园内出现新冠病例往往有大面积传染的风险，还可能成为家庭传播的重要来源。为此提出了基于班级减少接触策略，用于校园疫情防控，该策略可理解为依据班级结构对校园人群进行社团划分后，减少社团间或社团内的人际接触。研究结果表明，在减少同等接触人数或接触时长的前提下，基于社团结构的有差别减少接触策略可取得更好的疫情防控效果，使得校园人群的感染峰值和致病总人数进一步降低。

关键词： COVID19；疾病传播；社团结构；SEIR模型；校园疫情

中图分类号： TP391；R183.3文献标识码： A

Suppression of COVID19 Campus Spreading Based on Community Structures

GAO Tian， XU Xiaoke

（College of Information and Communication Engineering， Dalian Minzu University， Dalian 116600， China）

Abstract：The campus is a special crowded place. If a patient with covid19 appears on campus， there is often the risk of large-scale infection， and it may also become an important source of family transmission. This paper proposes a class-based contact reduction strategy for campus epidemic prevention and control. This strategy can be understood as reducing human contact between and within communities after the campus population is divided into groups according to the class structure. The research results show that， on the premise of reducing the same number of contacts or contact time， differential contact reduction strategies based on community structure can achieve better epidemic prevention and control effects， making the infection peak and the total number of disease-causing population fell further on campus.

Keywords： COVID19; disease spread; community structure; SEIR model; campus outbreak

0 引言

自2019年底新冠疫情爆发以来，中国政府迅速行动，提出了“外防输入，内防反弹”总策略和“动态清零”总方针，取得了世界瞩目的疫情防控成果。但随着后期阿尔法、德尔塔、奥米克戎等传染性更强变种的出现［1］，使得国内疫情态势变得严峻起来，不但家庭聚集性疫情频发，而且校园聚集性疫情也多了起来［24］。在此形势下，校园疫情防控越来越成为一个热点话题，如何保证疫情期间中小学正常的教学活动成为亟待解决的社会问题。

当新冠肺炎病例在校园内出现时，需要及时施加有效的防控措施。由于各种药物性干预措施都无法完全阻止疫情传播，因此各种非药物性干预措施，如群体免疫［56］、数字跟踪［79］、对所有人实行无差别的减少接触［1013］等措施被提出。相比群体免疫策略和数字跟踪策略，无差别减少接触策略是目前非药物干预措施中使用最为广泛的防控策略，通过降低人群之间的接触来延缓或者阻断新冠传播。如Laura等通过无差别减少25%、75%、95%的物理接触措施，发现三种减少比例下总感染人数均会下降，且随着减少比例的增大总感染人数也会快速下降［10］。Petrnio等提出了一种新的基于covid-SEIR的传染病模型，减少30%～90%（以10%递增）的接触比例，结果表明减少接触比例越大感染总人数也越少［11］。此外，Calistus等［12］和Saif等［13］的研究，通过社区接触率参数基线值降低的方式来衡量无差别减少接触措施的影响。虽然上述无差别减少接触措施在防控疫情上有一定效果，但考虑到新冠病毒变体的高传播性及在校园这种封闭环境下极快的传播速度，很多时候学校只能选择停课封校来缓解校园疫情，而停课隔离的大量学生返回家庭后会带来极大的经济和社会成本，甚至不利于整个社会的稳定［14］。针对此问题，需要制定更加科学有效的防控措施去应对新冠肺炎在校园的传播。

在一些信息传播研究中，研究人员会基于网络的社团结构制定策略来控制社会舆论传播［15］，隐私信息传播［16］等，受此启发，在校园新冠传播研究中也可考虑基于社团结构来抑制传播。由于校园一般存在明显的班级结构，校园人群在同一班级内的接触较多，在不同班级间的接触则较少，且校园的班级信息易于获取，所以不同于信息传播研究中使用社团检测算法来检测网络的社团结构，在校园新冠传播研究中可考虑依据班级结构来进行社团划分。基于班级结构进行社团划分时，将同属一个班级的人划分到一个社团，然后减少社团间或社团内的人际接触来控制校园新冠传播。

新冠通过真实的线下人际接触进行传播，而线下人际接触网络往往具有社团结构，基于此，本文首先通过带有社区结构的真实线下人际接触数据来构建真实校园新冠传播环境即新冠传播模型，然后将减少接触分为减少接触人数与减少接触时长两种手段在这个新冠传播模型下仿真模拟进行研究。相对于无差别减少接触策略，结果表明考虑减少接触人数时，减少社团内的接触防控效果最好；而考虑减少接触时长时，减少社团间的接触防控效果最好。当社团间和社团内减少接触联合使用时，针对减少接触人数指标，先减少社团内再减少社团间的接触防控效果最好；而针对减少接触时长指标，先减少社团间再减少社团内的接触防控效果最好。本研究考虑了班级具有操作性的社团结构在新冠防控中的作用，能够为制定有效的校园疫情防控策略提供参考，更好的平衡校园疫情防控和学生正常学习秩序。

1 研究数据与方法

1.1 真实人际接触数据和时效网络的构建

由于技术和数据采集的限制，以前很多研究中使用网络模型、线上社交网络或者问卷调查数据构建了人工合成传播环境进行新冠或其他疾病传播研究［1719］，并没有使用人际之间的真实接触数据。

近些年随着信息科技和物联网技术的快速发展，已经能使用高科技手段采集适用于疾病传播研究的真实线下接触数据，比如Wi-Fi热点数据［20］、GPS数据［21］、定制射频标签（RFID）数据［2223］等。基于Wi-Fi热点在采集时可能会因为系统设定或者电量问题不受控的关闭热点从而导致线下接触数据丢失，GPS设备则会面临定位精度不准确而导致数据精确度较差。采集效果更好的是通过定制的射频标签（RFID），在采集人群接触信息时，个体可通过佩戴定制的RFID传感器以20s的时间分辨率检测并记录个体间的近距离接触，最终收集的数据既包含接触边信息（可用于计算个体的接触人数），也包含接触次数信息（可用于计算个体间的接触时长）。本文构建新冠传播环境时使用了RFID设备收集的网络规模较大的小学真实线下接触数据集［22］和高中真实线下接触数据集［23］。

真实小学数据集记录了242名学生在校内2天的线下接触数据，高中数据集记录了329名学生在校内5天的线下接触信息。其中小学人群共有11个班级125 773条接触数据（班级内部107 599条，班级间18 174条），高中人群共有9个班级188 508条接触数据（班级内部173 558条，班级间14 950条），每条数据代表一次近距离接触。这种近距离接触会存在相同的人之间多次接触的情况，通过去除这类重复的接触数据获得接触边总数的数据，用于表示数据集网络中人与人之间共有多少接触边，小学人群共有8 317条接触边（班级内部3 769条，班级间4 548条），高中人群共有5 818条接触边（班级内部3 578条，班级间2 240条）。

考虑到校园环境下，老师同学一般都周一到周五在学校工作学习，周末居家休息，因此本研究基于上述两个数据集构建以周为周期的人际接触时效网络作为新冠传播环境，而后在这个新冠传播环境下进行仿真实验。对于小学数据集来说，原始数据只有2天非双休日的接触数据（day1，day2），所以本文基于2天的原始数据将非双休日接触数据扩充为5天（周一至周五分别为day1，day2，day1，day2，day1），另外双休日校园人群一般不会在校园内聚集，故仿真实验中不构建在双休日的接触网络，认为个体在周末相互不接触。高中数据集虽然有5天非工作日的接触数据，但第1天数据并不完整，只有5h的数据，本文在构建网络时使用第5天数据替代了第1天数据并在后续的仿真中验证了替代数据并不会影响数据在时间上的关联，双休日的处理同小学数据集一样。

构建好的时效网络中包含校园人群的接触信息，这些接触信息既可以算出每个人的接触人数，也可以根据记录的接触信息条数来计算校园人群人与人之间的接触时长。由于原接触数据集是每20s收集一次接触信息的结果，其中会存在接触不连续的情况，如果将40s或更大的时长定义为一次连续接触的时长，那么将会出现冲突，因此本文将20s定义为一次接触的接触时长。以图1为例，a与b存在两次近距离接触，与d存在一次近距离接触，那么a的接触人数为2，a与b的接触时长为2*20s=40s，a与d的接触时长为1*20s=20s。同理，也可以算出b、c、d的接触人数以及与他人的接触时长。

1.2 传播模型

常用的传染病模型有SI［24］、SIS［25］、SIR［26］、SEIR［27］等模型，每种模型的传染病应用场景不同。SI模型适用于一旦患病就难以恢复的传染病研究；SIS模型适用于患病后可治愈，但治愈后有再次感染疾病可能的传染病研究；SIR模型适用于患病后可恢复为免疫态，难以再次感染病毒的传染病研究；SEIR模型可以看作增加了潜伏期（E）的SIR模型，潜伏期内无任何感染症状，一旦过了潜伏期就会变为有症状的感染态，但最终可以恢复为免疫态。

新冠传染属于有潜伏期的传染病，且治疗好后在当前传染期中再次感染的情况非常罕见［28］，故可以视为在经历过感染态后，不会再次成为易感态，只会成为免疫态的传染病。因此针对新冠疫情的模拟仿真，使用SEIR模型最为合适。个体在SEIR模型中共有四种状态：易感态（S）、潜伏态或者暴露态（E）、感染态（I）、免疫态（R）。初始情况下，所有人都处于易感态，然后随机生成一个感染新冠的患者，感染态的患者通过人际接触感染处于易感态的人；处于易感态的人一旦被感染，就会进入潜伏期，潜伏期内没有症状但是会有传染性；在患者渡过潜伏期后，进入感染态，感染态同样有传染性；最后在经历痊愈期后患者将会被治愈，成为免疫态。SEIR模型的感染率、潜伏期和痊愈期参数的具体设置如下：

1）感染率：基本繁殖数R0是传染病学的一个重要指标，用于衡量一个群体中通过初始感染的个体直接感染的人数［29］。传统的SEIR模型的感染率设置可依据传染病的R0来设定平均感染率β-作为最终使用的仿真模拟参数，初始时设置任意感染率，然后仿真模拟1 000次，通过得出的初始感染的个体直接感染的人数大小与文献查到的基本繁殖数R0的比值乘上初始设置的任意感染率得出最终的平均感染率β-。虽然可以通过上述过程得出平均感染率β-，然而恒定的感染率参数并不适用于新冠病毒的传播。根据Barry等的研究，动物在感染新冠后每日的病毒排放量En并不相等，而是随着时间推移有先快速增加后缓慢下降的趋势（day0-day14病毒排放量依次大致为0，10，158，501，1 995，1 500，1 000，658，316，160，3.98，3，2，1，0，单位：equivalent/ml），病毒排放量越大传染性就越强［30］。本研究依据上述动物每天病毒排放量大小En来近似患者每一天的传染率。首先计算感染期间病毒脱落量对数（以10为底）的平均值，计算公式：

E-=∑Nn=1lgEnN（1）

其中，N为被感染期间具有传染能力的总天数（13天），En为患者在被感染后第n天时的病毒脱落量。通过E-可以计算每日传染率，公式：

βn=β-·lgEnE-（2）

其中，βn为第n天的感染率，β-为被感染期间的平均感染率。现有研究表明，新冠病毒传播的R0值在2.24到5.71之间［3132］，本文将小学和高中环境下的R0取值为4，之后在高中和小学环境下设置不同的感染率进行仿真模拟以计算R0值，最终仿真得出当平均感染率为2.8*10-4s-1时可满足R0为4的条件，而后基于β-和病毒每日脱落量来计算每日的感染率。

2）潜伏期时长：据钟南山团队的研究，感染新冠后患者处于潜伏状态天数的中位数为4天［33］，故本文将仿真模型潜伏期时长参数设置为4天。

3）痊愈期时长：患者渡过潜伏期后进入感染态，进入感染态的患者会被立即送入医院隔离治疗，不再接触其他人员，在医院治疗的平均住院时间为10天［34］。

1.3 衡量指标

为了衡量不同减少接触策略对于新冠疫情防控效果的影响，本文采用感染峰值和致病总人数这两个指标，它们都是值越小说明对应的策略越具有优势。

1）感染峰值。感染峰值是指截至第i日处于潜伏或感染态的总人数Ni（i= …，n）中的最大值。使用感染峰值作为指标是衡量防控措施有效性的常见指标，感染峰值的降低会减轻医疗系统的瞬时压力，可验证防控策略的有效性。

2）致病总人数。致病总人数是指从疫情爆发到疫情结束总的感染人数，致病总人数的降低可减少社会在治疗患病人员的成本方面的投入。

2 基于社团结构减少接触对校园疫情影响

2.1 减少接触简介

1）减少接触人数：此手段可理解为有些人能不见就不见，直接断开与这些人的连接，比如减少接触前a与b交互2次，减少接触人数后两者1次都不交互。对应到图1的时效网络上，减少a与b的接触时，将会直接断开a与b之间的接触，相应地，a与b的接触时长也降为0。

2）减少接触时长：此手段可理解为减少个人之间接触的总时长，比如减少接触前a与b有2次交互，相应的接触时长为2*20s=40s，现在减少为只有1次交互，接触时长变为了1*20s=20s。对应到图1的时效网络上，减少a与b的接触时，将会使交互次数变为1次，但由于仍存在接触，所以他们的接触人数未发生变化。值得注意的是，当a与b的交互次数减为0时，接触时长会变为0*20s=0s，此时相当于断开了a与b之间的接触，他们的接触人数会各自减1。

2.2 基于社团结构减少接触

新冠疫情在校园人群中通过人际接触网络进行传播。一般情况下，校园环境下都存在明显的班级结构，人们在班级内的接触人数较多、接触时长较长，在班级间的接触人数较少、接触时长较短，因此可考虑校园人群的班级结构来改进无差别减少接触策略。有可能减少班级间的接触控制疫情传播效果比较明显，因为班级间的接触断开代表着大的学生群体间不再接触。有可能减少班级内的接触控制疫情传播效果更好，因为班级内的学生接触比较密切。考虑班级结构的减少接触策略可看作首先依据班级结构对校园人群进行社团划分，将同一班级的人看作一个社团，然后基于划分出的社团结构来减少接触。

基于社团结构的减少接触策略可以分为减少社团内接触、减少社团间接触两种手段。实施策略首先要根据班级结构对校园人群进行社团划分，而后将校园人群分为社团间人群和社团内人群，分别用于减少社团内接触、减少社团间接触的仿真实验，同时在校园人群上进行无差别减少接触的仿真实验作为对比。考虑到社团间和社团内人群的总接触人数或总接触时长不相同，为了对比三种减少接触方式在同等减少接触人数数量或接触时长下的效果，所以还需设置一下减少接触的上限。本节将减少上限设为社团内人群和社团间人群的总接触人数或总接触时长的最小值，减少接触人数上限用p表示，减少接触时长上限用t表示。依照此规则，当减少接触人数时，小学人群减少上限p设置为3 769人，高中人群减少上限p设置为2 240人，当减少接触时长时，小学人群减少上限t设置为18 174*20s，高中人群减少上限t设置为14 950*20s。

通过上述介绍，首先确定了小学人群和高中人群减少接触的上限值，并划定了社团内人群、社团间人群，之后将分别实施三种减少接触方式的仿真实验：1）社团内减少：在社团内人群中随机选择要减少接触的人数或时长，进行基于社团结构的减少社团内接触的仿真实验；2）社团间减少：在社团间人群中随机选择要减少接触的人数或时长，进行基于社团结构的减少社团间接触的仿真实验；3）无差别减少：在校园人群中随机选择要减少接触的人数或时长，进行无差别减少接触的仿真实验。

基于上述三种减少接触方式，分别进行减少0.0p-1.0p（以0.1递增）的接触人数或减少0.0t-1.0t的（以0.1递增）接触时长的仿真实验，减少0.0p或0.0t对应无减少接触改动的情况。根据仿真实验结果，本文比较两种衡量指标的结果，一种表示当前感染峰值随减少接触人数或接触时长增大而变化的情况，另一种表示每种减少不同接触人数或接触时长下致病总人数的变化情况。所有仿真实验都在Windows10，python3.8的环境下进行了1 000次的重复模拟以排除偶然因素的影响。

2.3 减少接触人数对校园疫情传播影响

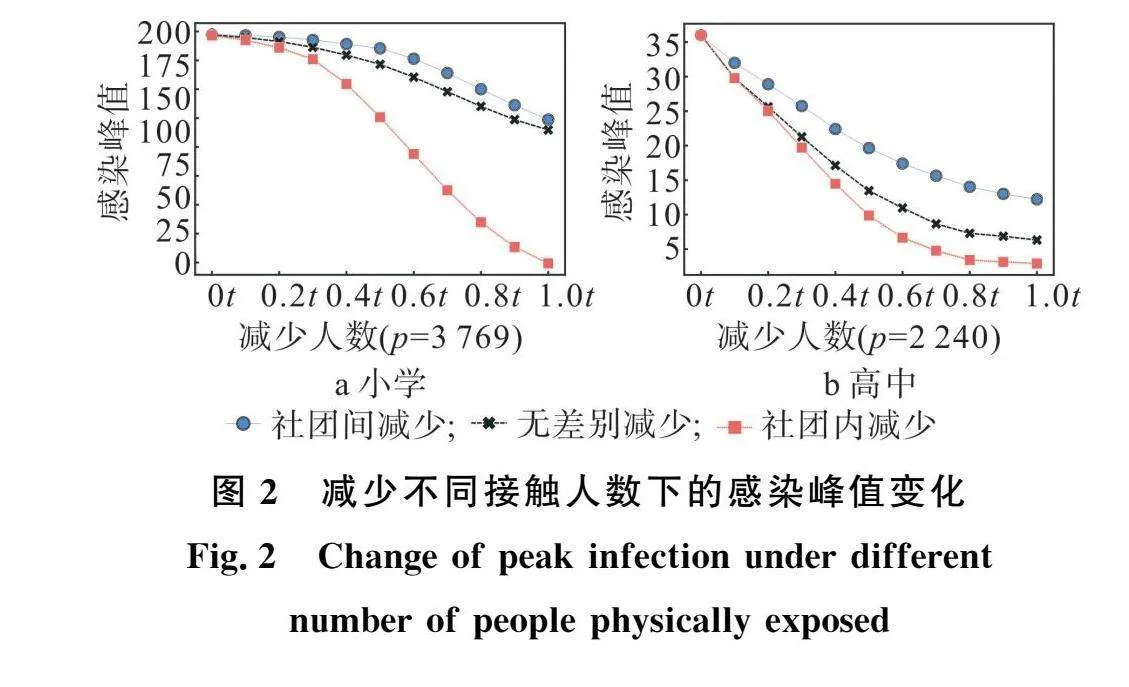
减少接触是校园面临疫情传播威胁时可采取的防控措施，首先对减少校内人群的接触人数进行探究，设置小学人群减少上限p为3 769人，高中人群减少上限p为2 240人。图2代表小学人群（左）和高中人群（右）在减少不同接触人数下使用不同减少接触方式的感染峰值变化结果。

由图2可知，当减少接触人数时，与无改动措施相比，虽然社团间、社团内或者无差别减少接触均会降低感染峰值，但减少社团内接触人数峰值降低幅度是最大的。分析产生这一结果的主要原因如下。当减少人群接触人数的同时，也会相应减少人群的接触时长，而人与人之间的接触时长越短疫情越难以传播。社团内人群之间的平均接触时长相比社团间人群或者整个校园人群的平均值都要长，所以当减少相同数量的接触人数时，优先社团内减少更能抑制疫情的传播，减低疫情传播的峰值。

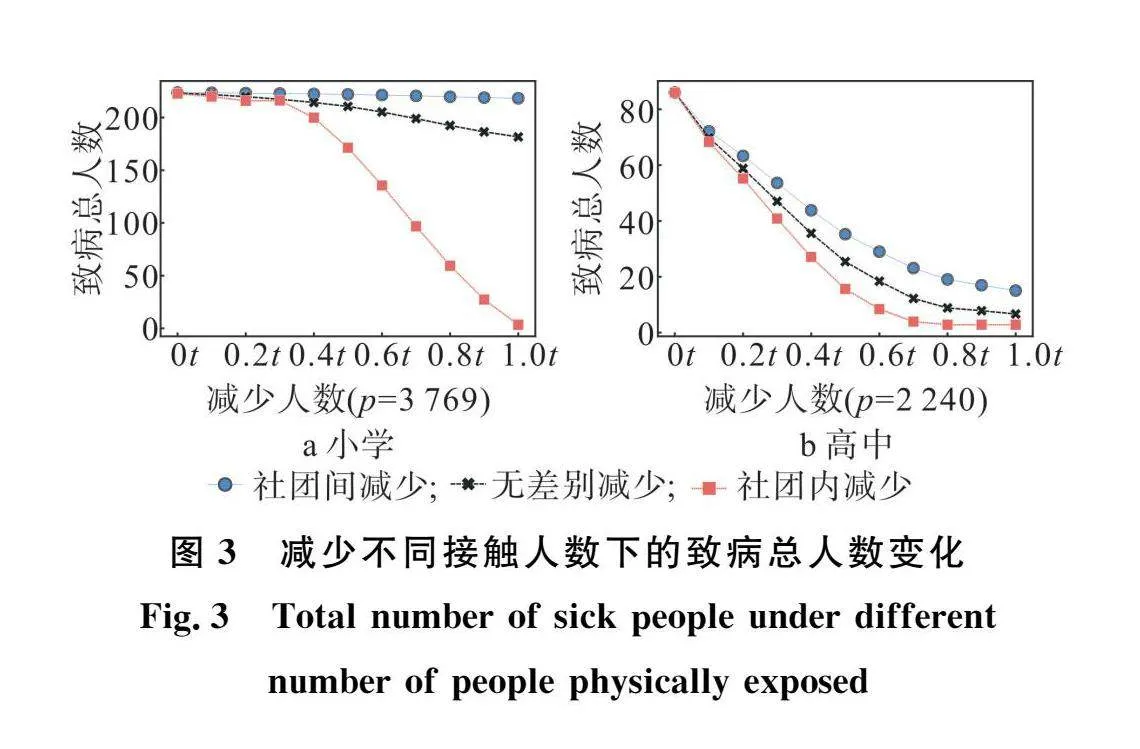
图3代表小学人群和高中人群在减少不同接触人数下使用不同减少接触方式的致病总人数变化结果。从小学人群结果图中可以看出，随减少接触人数的增大，减少社团内接触对降低致病总人数的效果会越来越显著，另外两种减少接触方式未能有效降低致病总人数。高中人群的结果表明，3种减少接触方式均会有效降低致病总人数，但社团内减少的效果最好。我们分析产生图3这一结果的原因与产生图2结果的原因一致，都是因为社团内人群的平均接触时长最大，所以当减少相同数量的接触人数时，优先社团内减少的效果最优。

2.4 减少接触时长对校园疫情传播影响

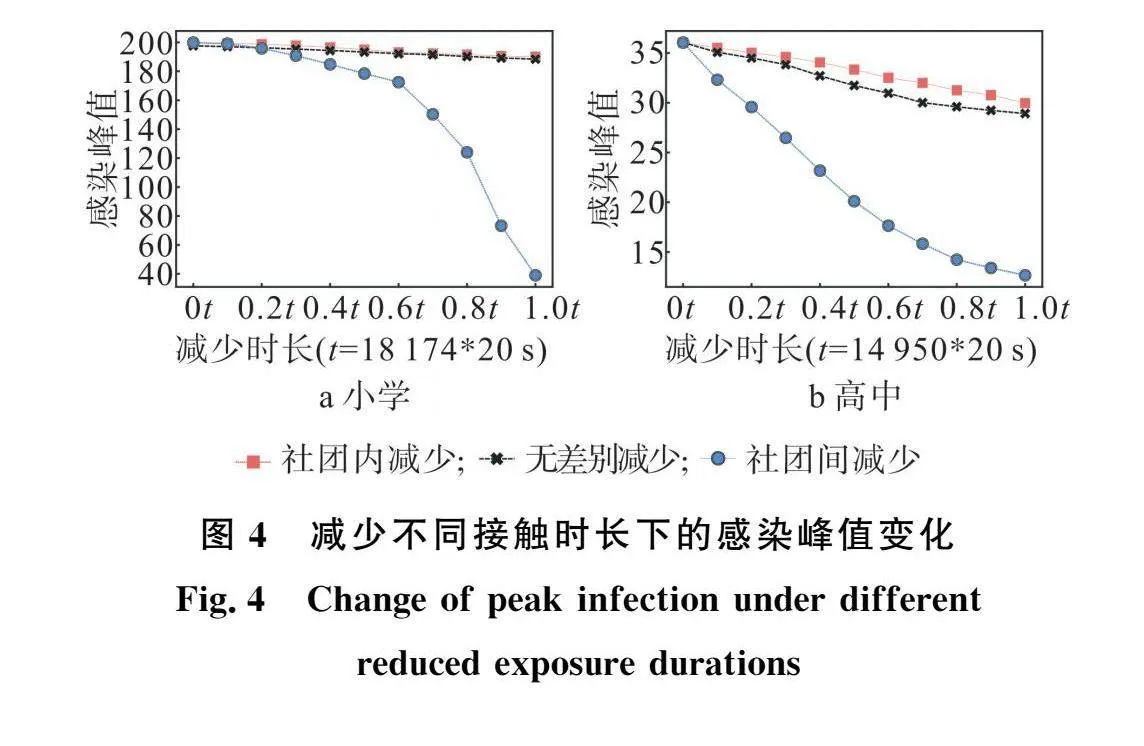
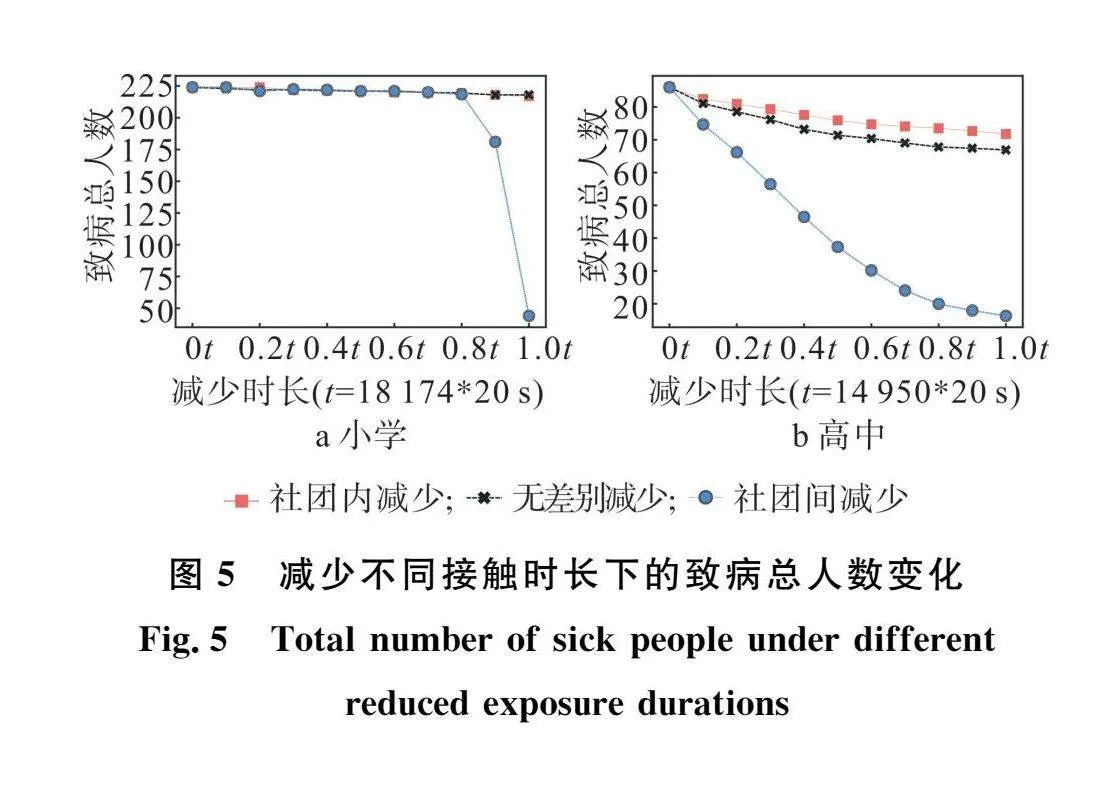
2.3节中分析了减少接触人数对校园疫情的传播影响，本小节将分析减少接触时长对校园新冠疫情的传播影响，在本小节中小学人群减少接触时长上限t设置为18 174*20s，高中人群减少上限t设置为14 950*20s。小学人群和高中人群减少接触时长的感染峰值变化结果如图4所示。

从图4中的曲线可以看出，无论是在小学人群还是高中人群，相比于其他两种减少接触方式，减少社团间接触时长的仿真结果感染峰值最低，且随着减少接触时长的增大，这个效果越来越明显。但同时也可以发现当使用减少接触时长的手段时，社团内减少或无差别减少的方式在感染峰值上变化不大，本文对这一现象分析的原因如下。社团内人群或整个校园人群的平均接触时长远大于社团间人群的平均接触时长，所以减少相同的接触时长对社团间人群的影响比较大，对社团内人群的影响比较小。由于社团间人群受影响较大，使得病毒难以从一个社团传播到另一个社团，最终只能在一个或少数几个受影响的社团内进行传播，从而感染峰值下降的效果明显。与此同时，由于社团内人群或整个校园人群的平均接触时长较大，所以减少社团内或无差别减少都未能对新冠在社团内人群或整个校园人群的传播产生显著影响。

小学人群和高中人群减少不同接触时长下致病总人数的变化如图5所示。由5可知，对于社团内减少或无差别减少方式来说，致病总人数随减少接触时长增大变化不大，这与图4的结论相同。但不同的是，小学人群在减少社团间接触方式的结果上存在一个0.8t的临界点，减少接触时长未超过0.8t时，致病总人数未有明显变化，超过0.8t时，致病总人数开始快速下降。我们分析存在0.8t临界点的原因如下。当小学人群减少接触时长不超过0.8t时，疫情仍能轻易的从一个社团传播到其他社团，使得减少社团间的效果并不明显。当减少接触时长超过0.8t时，社团间疫情传播开始被有效抑制，从而使得致病总人数不断下降。

3 基于社团结构减少接触人数和接触时长实验扩展

上节在校园环境下的减少接触仿真实验可看作只减少社团间接触或只减少社团内接触进行校园疫情防控进行研究，有时候并不一定能完全达到彻底消灭疫情传播的效果。在疫情比较严重或者基本再生数比较大的情况下，需要将减少社团间接触与减少社团内接触结合起来使用用来校园疫情防控，这种方式可以减少更多的接触，同时达到更好的防止疾病传播的效果。此时，我们探究是先减少社团间接触再减少社团内接触效果好，还是先减少社团内接触再减少社团间接触效果好。

扩展实验将减少接触上限提高到整个校园人群的总接触人数（小学为8 317人，高中为5 818人）和总接触时长（小学为125 773*20s，高中为188 508*20s）。仿真实验的思路：1）先减少社团内接触，再减少社团间接触：优先减少社团内人群的接触人数或接触时长，当社团内的接触人数或接触p时长减为0时，再减少社团间的接触人数或接触时长。2）先减少社团间接触，再减少社团内接触：优先减少社团间人群的接触人数或接触时长，当社团间的接触人数或接触时长减为0时，再减少社团内的接触人数或接触时长。3）整个校园人群无差别减少接触：在整个校园人群中无差别减少接触人数或接触时长。

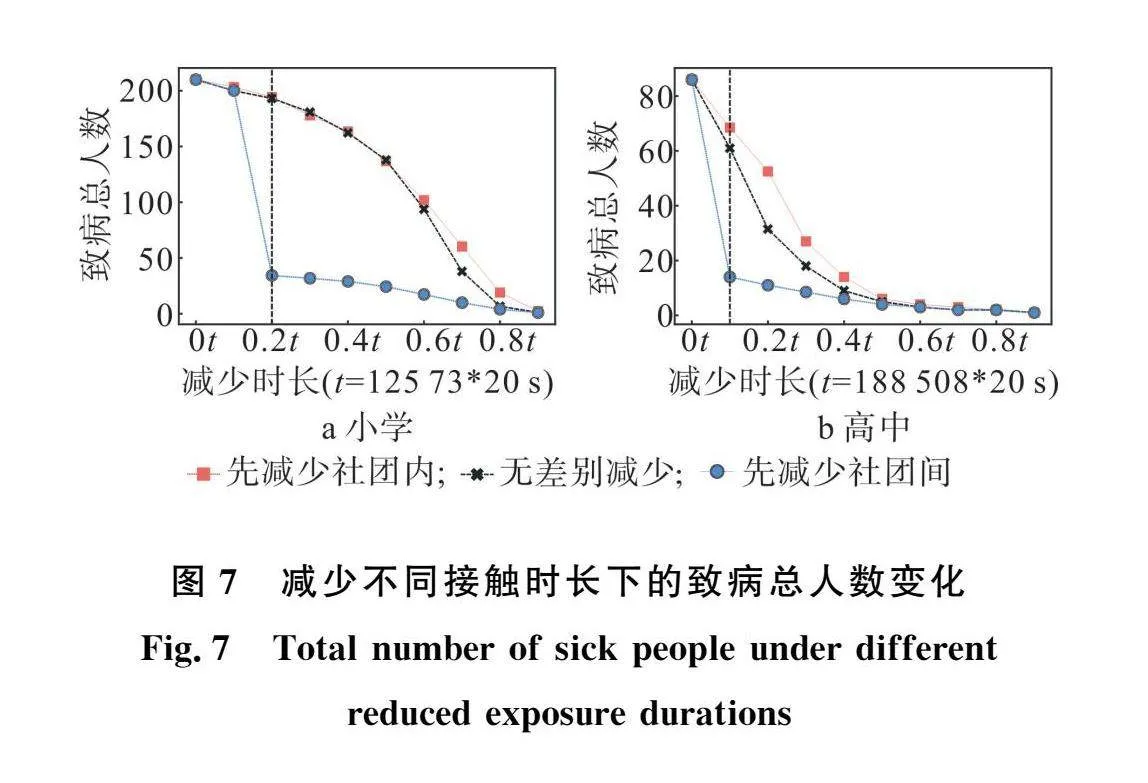
在本节的实验中，使用减少接触人数的手段时，设置小学人群减少人数上限p为8 317人，高中人群减少人数上限p为5 818人，致病总人数随减少接触人数增大的变化情况见图6。使用减少接触时长的手段时，设置小学人群减少时长上限t为125 773*20s，高中人群减少时长上限t为188 508*20s，致病总人数随减少接触时长增大的变化情况见图7。两图中竖虚线对应X轴的位置为上节减少接触人数或减少接触时长对比实验的上限值点，减少接触人数或减少接触时长大于这个上限值点时，可以观察到先减少所有社团间的接触再减少社团内的接触、先减少所有社团内的接触再减少社团间的接触、无差别减少接触三者的防控疫情传播效果。另外因为减少1.0p或者1.0t的接触时将会断开网络中所有的接触，此时采取任何措施都不能使得疫情传染开来，所以本文并未展示减少1.0p或者1.0t的结果。

由图6可知，使用减少接触人数的手段时，相比于另外两种策略，先减少社团内再减少社团间接触效果最优。对于小学人群，当减少接触人数为0.5p时，先减少社团内再减少社团间接触人数的策略已经可以将致病总人数控制在10人以下，有效控制了疫情在小学人群中的传播。对于高中人群，当减少接触人数为0.3p时，先减少社团内再减少社团间接触人数的策略同样将致病总人数控制在10人以下，阻断了疫情在高中人群中的传播。另外从图中的竖虚线可以看出，使用先减少社团内再减少社团间的策略，当断开所有社团内的接触时，已经可以阻断校园疫情的传播，无需再进一步减少社团间的接触。

由图7可知，使用减少接触时长的手段时，相比于另外两种策略，先减少社团间再减少社团内接触效果最优。对于小学人群和高中人群，当减少接触时长分别为0.2t和0.1t时，先减少社团间再减少社团内的策略已经极大降低了致病总人数，在此基础上，如果继续减小接触，致病总人数会进一步下降。最后从图中的竖虚线可以看出，当断开社团间的所有接触时，虽已经极大降低了致病总人数，但并没有完全彻底消灭校园疫情，如果想达到更好的疫情防控效果可考虑进一步减少社团内的接触。

通过本节的仿真实验可以得出结论，当同时减少社团内和社团间的接触时，单考虑减少接触人数，先减少社团内的接触再减少社团间的接触控制校园疫情传播效果最好；单考虑减少接触时长，先减少社团间的接触再减少社团内的接触控制校园疫情传播效果最好。在实际应用中，当校园面临疫情威胁，可以先采用单独减少社团内接触人数或单独减少社团间接触时长的策略来预防校园疫情大规模爆发。当校园已经发现疫情，应当立即采取更严格的防控措施，同时使用社团内减少和社团间减少策略来控制新冠疫情传播。

4 结语

本文基于真实校园中人际接触数据构建了小学和高中新冠传播环境，使用符合真实新冠传染率规律的SEIR模型仿真模拟了无差别减少接触策略与基于社团结构减少接触策略在校园内的新冠传播情况，对各种减少接触策略的仿真结果进行了对比分析。

结果表明，当使用减少校园人群接触人数手段时，优先减少社团内的接触在降低校园人群致病数和感染峰值上效果最好；当使用减少校园人群接触时长手段时，优先减少社团间的接触效果最好。最后的扩展实验表明，当社团间和社团内减少接触同时使用时，单考虑减少接触人数，先减少社团内再减少社团间的接触防控效果最好；单考虑减少接触时长，先减少社团间再减少社团内的接触防控效果最好。

综上所述，当校园人群面临新冠传播的威胁时，在防止校内传染源出现的同时，也应当在校内实行合适的防控策略，较优的策略是考虑校园人群的班级结构，先对校园人群进行社团划分，然后根据实际情况优先减少校园人群社团内的接触人数或社团间的接触时长，实行基于社团结构的减少接触策略。在此策略下，一旦病毒在校内开始传播，相比无差别减少接触策略，基于社团结构的减少接触策略可以取得更好的疫情防控效果。当然这些只是校园层面采取的防控措施，当面临疫情威胁时，也要减少与社会人员的不必要接触，做好校园人群的防护工作。

参考文献：

［1］HEMMER C J， LBERMANN M， REISINGER E C. COVID19： epidemiologie und mutationen［J］. Der Radiologe， 202 61（10）： 880887.

［2］温竞华， 宋晨. 当前疫情形势如何？校园防疫如何做？［N］. 新华每日电讯， 20220507（4）.

WEN J， SONG C. What is the current situation of the epidemic？ How to do campus epidemic prevention？［N］. Xinhua Daily Telegraph， 20220507（4）.

［3］陈晶. 落细防控举措，抓好社区和校园疫情防控［N］. 人民政协报， 20220511（5）.

CHEN J. Implement detailed prevention and control measures， and focus on community and campus epidemic prevention and control［N］. CPPCC DAILY， 20220511（5）.

［4］郭丽菲. 太原学院疫情防控不松懈，筑牢校园“安全网”［N］. 山西青年报， 20220421（8）.

GUO L. Taiyuan University remains vigilant in epidemic prevention and control， building a strong campus "safety net"［N］. Shanxi Youth Daily， 20220421（8）.

［5］HABIB H. Has Sweden’s controversial covid19 strategy been successful？［J］. Bmj， 2020， 369： m2376.

［6］贝壳， 陆默. “群体免疫” 策略： 科学还是赌博［J］. 世界科学， 2020 （5）： 1012.

BEI K， gdIuE1plgzkltuVEwuDg3w==LU M. "Group immunity" strategy： science or gambling［J］. World Science， 2020（5）： 1012.

［7］FERRETTI L， WYMANT C， KENDALL M， et al. Quantifying SARS-CoV2 transmission suggests epidemic control with digital contact tracing［J］. Science， 2020， 368（6491）： eabb6936.

［8］BAKER A， BIAZZO I， BRAUNSTEIN A， et al. Epidemic mitigation by statistical inference from contact tracing data［J］. Proceedings of the National Academy of Sciences， 202 118（32）： e2106548118.

［9］SOLDANO G J， FRAIRE J A， FINOCHIETTO J M， et al. COVID19 mitigation by digital contact tracing and contact prevention （app-based social exposure warnings）［J］. Scientific Reports， 202 11（1）： 18.

［10］ MATRAJT L， LEUNG T. Evaluating the effectiveness of social distancing interventions to delay or flatten the epidemic curve of coronavirus disease［J］. Emerging Infectious Diseases， 2020， 26（8）： 17401748.

［11］ SILVA P C L， BATISTA P V C， LIMA H S， et al. COVID-ABS： an agent-based model of COVID19 epidemic to simulate health and economic effects of social distancing interventions［J］. Chaos， Solitons & Fractals， 2020， 139： 110088.

［12］ NGONGHALA C N， IBOI E， EIKENBERRY S， et al. Mathematical assessment of the impact of non-pharmaceutical interventions on curtailing the 2019 novel Coronavirus［J］. Mathematical Biosciences， 2020， 325： 108364.

［13］ ULLAH S， KHAN M A. Modeling the impact of non-pharmaceutical interventions on the dynamics of novel coronavirus with optimal control analysis with a case study［J］. Chaos， Solitons & Fractals， 2020， 139： 110075.

［14］ EICHENBAUM M S， REBELO S， TRABANDT M. The macroeconomics of epidemics［J］. The Review of Financial Studies， 202 34（11）： 51495187.

［15］ SUN J， HAO Y. Hierarchicalsemantic community detection in information networks： a complete information graph approach［J］. Tehnicˇki Vjesnik， 2019， 26（6）： 17001706.

［16］ 张长伦， 宁楠， 金占勇. 基于双重网络社团结构的隐私信息传播模型［J］. 信息技术， 2018（9）： 3843.

ZHANG C， NING N， JIN Z. Privacy information spreading model based on community structure on dual netword［J］. Information Technology， 2018（9）： 3843.

［17］ MATRAJT L， LEUNG T. Evaluating the effectiveness of social distancing interventions to delay or flatten the epidemic curve of coronavirus disease［J］. Emerging Infectious Diseases， 2020， 26（8）： 1740.

［18］ SALATH M， JONES J H. Dynamics and control of diseases in networks with community structure［J］. PLoS computational biology， 2010， 6（4）： e1000736

［19］ ZHANG J， JIN Z. Epidemic spreading on complex networks with community structure［J］. Applied Mathematics and Computation， 2012， 219（6）： 28292838.

［20］ ZHOU M， MA M， ZHANG Y， et al. EDUM： classroom education measurements via large-scale WiFi networks［C］//Proceedings of the 2016 acm international joint conference on pervasive and ubiquitous computing. Heidelberg Germany， 2016： 316327.

［21］ WANG R， CHEN F，CHEN Z， et al. StudentLife： assessing mental health， academic performance and behavioral trends of college students using smartphones［C］//Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing. Seattle Washington， 2014： 314.

［22］ STEHL J， VOIRIN N， BARRAT A， et al. High-resolution measurements of face-to-face contact patterns in a primary school［J］.PloS One， 201 6（8）： e23176.

［23］ MASTRANDREA R， FOURNET J， BARRAT A. Contact patterns in a high school： a comparison between data collected using wearable sensors， contact diaries and friendship surveys［J］.PloS One， 2015， 10（9）： e0136497.

［24］ BARTHLEMY M， BARRAT A， PASTOR-SATORRAS R， et al. Velocity and hierarchical spread of epidemic outbreaks in scale-free networks［J］. PhysicalReview Lletters， 2004， 92（17）： 178701.

［25］ QIN Y， ZHONG X， JIANG H， et al. An environment aware epidemic spreading model and immune strategy in complex networks［J］. Applied Mathematics and Computation， 2015， 261： 206215.

［26］ SALATH M， JONES J H. Dynamics and control of diseases in networks with community structure［J］.PLoS Computational Biology， 2010， 6（4）： e1000736.

［27］ 范如国， 王奕博， 罗明， 等. 基于SEIR的新冠肺炎传播模型及拐点预测分析［J］. 电子科技大学学报， 2020， 49（3）： 369374.

FAN R， WANG Y， LUO M， et al. SEIR-Based COVID19 Transmission Model and Inflection Point Prediction Analysis［J］. Journal of University of Electronic Science and Technology of China， 2020， 49（3）： 369374.

［28］ PEGHIN M， BOUZA E， FABRIS M， et al. Low risk of reinfections and relation with serological response after recovery from the first wave of COVID19［J］. European Journal of Clinical Microbiology & Infectious Diseases， 202 40（12）： 25972604.

［29］ WALLINGA J， TEUNIS P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures［J］. American Journal of Epidemiology，2004，160（6）：50916.

［30］ ROCKX B， KUIKEN T， HERFST S， et al. Comparative pathogenesis of COVID19， MERS， and SARS in a nonhuman primate model［J］. Science， 2020， 368（6494）： 10121015.

［31］ ZHAO S， LIN Q， RAN J， et al. Preliminary estimation of the basic reproduction number of novel coronavirus （2019-nCoV） in China， from 2019 to 2020： A data-driven analysis in the early phase of the outbreak［J］. InternationalJournal of Infectious Diseases， 2020， 92： 214217.

［32］ SANCHE S， LIN Y T， XU C， et al. High contagiousness and rapid spread of severe acute respiratory syndrome coronavirus 2［J］. Emerging Infectious Diseases， 2020， 26（7）： 14701477.

［33］ GUAN W， NI Z， HU Y， et al. Clinical characteristics of coronavirus disease 2019 in China［J］. New EnglandJournal of Medicine， 2020， 382（18）： 17081720.

［34］ WANG D， HU B， HU C， et al. Clinical characteristics of 138 hospitalized patients with 2019 novel coronavirus-infected pneumonia in Wuhan， China［J］. Jama， 2020， 323（11）： 10611069.

（责任编辑 李 进）