含参数不确定及时滞的线性系统自适应模型预测控制







摘要: 探讨了一类含参数不确定和输入延迟的约束多输入多输出线性系统的自适应模型预测控制问题。提出了一种基于时变更新率的自适应更新律,实现了在输入延迟的情况下更新估计系统的不确定参数。为了处理约束,将优化问题转换为源自于min-max优化可解的简单结构。此外,从理论上证明了闭环系统的渐近稳定性,并证明了提出的自适应模型预测控制策略是递归可行的。最后,数值模拟验证了所提方法的有效性。
关键词: 自适应模型预测控制;输入延迟;参数不确定性;离散时间系统
中图分类号: O231;TP273文献标识码: A
Adaptive Model Predictive Control for Linear Systems with Parametric Uncertainties and Time Delay
KONG Lingren QI Qingyuan2
(1.Institute of Complexity Science, Qingdao University, Qingdao 26607 China; 2. Qingdao Innovation and Development Center, Harbin Engineering University, Qingdao 266000, China)
Abstract:This paper investigates the adaptive model predictive control (MPC) for a class of constrained linear multiple-input multiple-output (MIMO) systems with parametric uncertainty and input delay. An adaptive update law based on time-varying updating rate is proposed, which enables the update of uncertain parameters in the presence of input delay. Consequently, to deal with the constraints, we convert the optimization problem into a solvable simple structure, which originates from the min-max optimization. Furthermore, theoretically, it is shown that the closed-loop system is asymptotically stable and the proposed adaptive MPC strategy is proved to be recursively feasible. Finally, numerical simulation is given to illustrate the efficacy of the proposed method.
Keywords: adaptive model predictive control; input delay; parametric uncertainty; discrete-time system
0 引言
模型预测控制(MPC)凭借其优异的性能和对约束的处理成为过程控制中一种高效的控制策略之一[12]。MPC技术的核心是通过解决有限时域优化问题来获得一系列最优的控制动作。值得注意的是,MPC模型的准确性可能会限制预测系统的性能[3]。事实上,系统中的不确定性很常见,它可能来自于多个因素,如模型参数的不确定性和输入延迟等。例如,在机器人控制[4]和化工控制[5]等高精度应用中,由测量误差、传感器限制和其他因素引起的模型参数不确定性会显著影响系统的性能表现和稳定性。此外,在飞行器控制[6]等实时响应的应用中,由传感器延迟、信号传输延迟和执行器延迟等引起的输入延迟可能会影响系统的安全性。
为了解决系统中存在的参数不确定性和输入延迟所带来的控制问题,一种高效的解决方案是自适应模型预测控制(Adaptive MPC)。近年来Adaptive MPC引起了广泛的关注,它考虑了参数不确定性,并把在线模型更新与传统的MPC控制器相结合,以在提高控制性能的同时满足约束条件。针对系统存在输入延迟的情况,可以用系统模型扩维来表示输入延迟的作用,从而分析和设计同时具有输入延迟和参数不确定的控制系统。对于Adaptive MPC现有的结论可分为不同的参数识别策略,包括但不限于最小二乘法[78],集合成员识别[913],神经网络[1415]和自适应更新律[1620]等。具体而言,文献[8]提出了一种参数估计策略,利用递归最小二乘算法同时进行参数识别和不确定性集合估计。文献[15]中提出的控制策略包括模型识别部分和预测部分,其中不确定参数在模型识别部分中通过具有特定结构的神经网络进行逼近。此外,文献[16]中引入了一种基于梯度下降的自适应更新定律,用于具有参数不确定性的无约束系统,其中未来状态的预测取决于对实际不确定系统的估计模型,这种方法的计算量相对于使用集合识别方法的策略[913]来说相对较小。在[16]的工作基础上,文献[17]提出了一种针对有参数不确定的约束系统的自适应模型预测控制策略,该策略针对具有特定模型结构的单输入离散时间线性系统。值得注意的是,在文献[20]中采用了一种自适应更新定律来更新有约束系统的不确定参数,同时考虑估计的参数集和系统约束条件,并利用min-max方法来优化问题,保证了递归可行性和闭环稳定性。
前面提到的文献[1620]已经采用Adaptive MPC来解决具有或不具有约束的参数不确定系统控制问题,但是关于同时具有输入延迟和模型不确定性系统的Adaptive MPC研究相对较少。实际上,常数时间输入延迟的情况经常发生,因此不能忽视该问题。本文列出了具有参数不确定性和输入延迟的约束优化问题所面临的技术困难。首先,由于计算复杂度很高,min-max优化的实现可能会非常困难。其次,在约束MPC中,由于最大误差上界的不确定性,导致很难保证闭环可行性和稳定性。最后,怎样以简单且高效的方式补偿输入延迟并与Adaptive MPC相结合,这是一个难点。
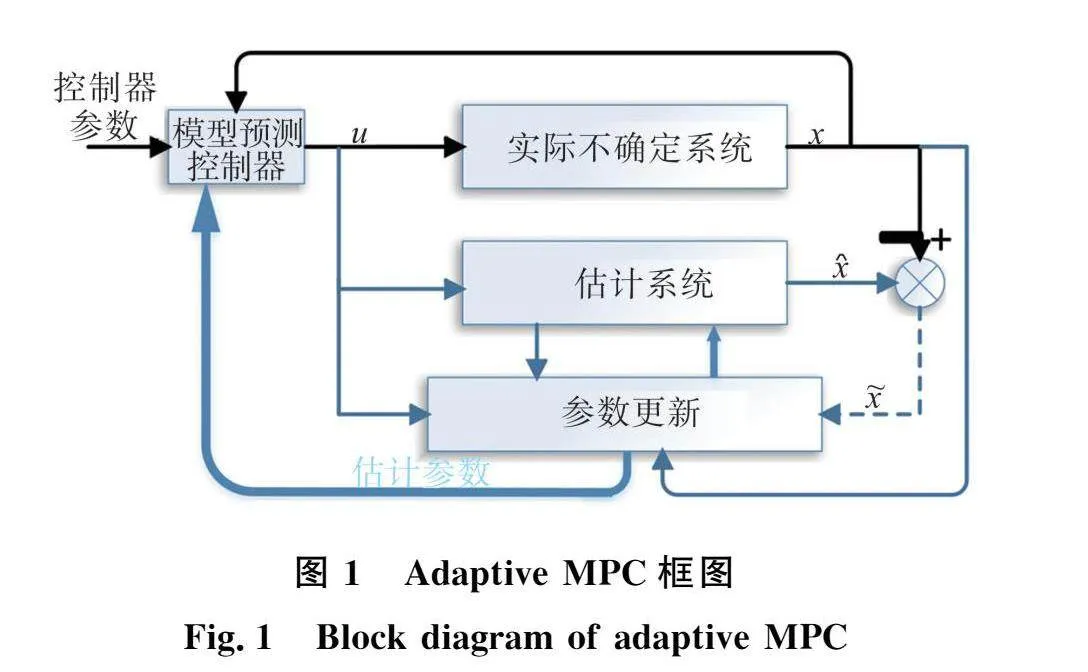
本文提出了一种自适应MPC策略,适用于具有常数参数不确定性和输入延迟的约束线性系统。通过引入基于时间变化的自适应更新律,本文的方法能够在输入延迟的情况下更新系统的估计参数,并证明了参数估计误差是有界的且状态估计误差是渐近稳定的。此外,提出的源于min-max优化的Adaptive MPC策略可以处理约束并获得数值解。最后,本文的方法能够通过一种扩维表示的系统模型来补偿输入延迟,同时保持递归可行性和闭环稳定性。本文提出的Adaptive MPC框图,如图1所示。
本文的贡献分为两点:1)本文不仅仅是文献[16],[17]和[20]的扩展,本文考虑了输入延迟对约束不确定系统的影响。2)本文引入了一种基于时变更新率的自适应更新律,它可以更新输入延迟系统的估计参数,并且证明了参数估计误差有界且状态估计误差是渐近稳定。
1 主要内容
1.1 问题阐述
考虑以下具有参数不确定和输入延迟的离散时间线性系统
xp(k+1)=Apxp(k)+Bpu(k-d)(1)
其中,xp(k)∈Rn为状态,up(k-d)∈Rm为控制输入;Ap∈Rn×n和Bp∈Rn×m为不确定性的系统矩阵;d∈N为已知的固定整数时间延迟。状态xp和控制输入u满足约束(2):
xp∈u∈u-(2)
其中,状态约束x-∈Rn和控制约束u-∈Rm为凸集。设计关于系统(1)的目标函数为
J(k)=∑Npi=1‖xp(k+i|k)‖2Qp+‖u(k-d+i-1|k)‖2Rp(3)
其中,Np为控制时域,Qp和Rp为适应维数的惩罚矩阵。
由于输入延迟的存在,系统的行为会受到前几个时间步的影响,使系统的动态特性变得更加复杂。为了更准确地描述系统(1)的行为,需要考虑历史的输入数据对系统的影响。因此,状态变量扩维是一种常用的方法,它引入了历史的控制输入数据,从而更准确地描述系统的动态特性。扩维系统模型为
x(k+1)=Ax(k)+Bu(k)(4)
其中,x(k)∈Rm×d+n为扩维的状态向量,A∈R(md+n)×(md+n)和B∈R(md+n)×m为扩维的系统矩阵,具体形式为
x(k)T=[u(k-1)T,u(k-2)T,…,u(k-d)T,xp(k)T]T
A=00…000I0…0000I…000…00…I0000…0BpAp, B=I0000
为了对扩维系统(4)中的控制输入性能进行限制和优化,目标函数(3)可以被式(5)的目标函数所代替
J(k)=∑Npi=1‖x(k+i|k)‖2Qc+‖u(k+i-1|k)‖2Rc(5)
其中,Qc=diag(0,…,0,Qp),Rc=Rp。
目标:设计一种含输入延迟和不确定性参数系统的Adaptive MPC策略,在每一个时刻解决有限时域优化问题,并在满足约束(2)的条件下得到最优控制序列U(k)*。优化表述如下:
U(k)*=arg minu∈u- J(x(k),u(k))(6)
s.t.
x(k+i|k)=Ax(k+i-1|k)+Bu(k+i-1|k)(7)
x(k+i|k)∈, u(k+i-1|k)∈u-(8)
x(k+Np|k)=0
在优化(6)中,已经用一种扩维系统模型(4)来表示输入延迟对系统带来的影响。但系统(4)中的矩阵A包含不确定参数Ap和Bp,导致求解以上优化问题并满足约束(2)非常困难。因此,需要考虑处理不确定性参数A并设计相应的优化算法来求解优化问题。
假设1 1)在每个采样时刻k,过去的控制输入是已知的,且当前时刻的状态xp(k)是可测量的;2)控制时域与预测时域相等;3)输入延迟步长d远小于控制时域Np;4)Qp和Rp是对称的且Qp≥0,Rp>0。
1.2 估计系统设计
系统(4)的估计系统可以设计为
(k+1)=(k)x(k)+Bu(k)(9)
其中,和分别为系统矩阵A和状态x的估计值。设置状态x的误差为=x-,那么在k+1时刻,状态估计误差为
(k+1)=(k)x(k)(10)
其中,(k)=A-(k)为系统矩阵A的估计误差。系统状态x(k)简化为Θ(k)=[up(k-d)Txp(k)T]T,相应地可以得到:
p(k+1)=(k)Θ(k)(11)
其中,(k)∈Rn×n+m为参数估计误差。(k),a和(k)为
(k)=a-(k)(12)
a=[Bp Ap](13)
(k)=[p(k) p(k)](14)
1.3 自适应更新率
本节的目标是设计一种自适应更新律,它可以使参数估计误差有界并且状态估计误差p渐近稳定。因此,定义一种关于状态估计误差的目标函数为
Ja((k))=p(k+1)Tp(k+1)=[aΘ(k)-(k)Θ(k)]T[aΘ(k)-(k)Θ(k)](15)
相对于Ja的梯度可以通过式(16)获得:
ΔJa((k))=-2p(k+1)Θ(k)T(16)
接下来介绍一种用于优化模型参数自适应更新律,以使目标函数(15)最小化。
(k+1)=(k)-λ(k)ΔJa()=(k)+2λ(k)p(k+1)Θ(k)T(17)
其中,λ(k)>0为时变的更新率,可以通过方程(18)获取λ(k)
λ(k)=arg minλ(k) Ja((k)+2λ(k)p(k+1)Θ(k)T)(18)
进一步
Ja((k)+2λ(k)p(k+1)Θ(k)T)λ(k)=-4p(k+1)Θ(k)TΘ(k)p(k+1)T+8λ(k)p(k+1)Θ(k)TΘ(k)Θ(k)TΘ(k)p(k+1)T=0
得到
λ(k)=12Θ(k)TΘ(k)(19)
公式(19)带入(17),可以得到具有时变更新率的自适应更新律:
(k+1)=(k)+1Θ(k)TΘ(k)p(k+1)Θ(k)T(20)
对于自适应更新律(20),p(k+1)在k+1时刻是可以被获取的。它可以通过计算(k+1)=xp(k+1)-(k)Θ(k)得到,其中xp(k+1)是在k+1时刻量测的系统状态。
引理1 考虑到带有输入延迟和参数不确定的系统(4),如果存在一个确定性的常数β>0,使得Θ(k)TΘ(k)≤β。对于自适应更新定律(6),这两个陈述成立:1)参数估计误差是最终有界的;2)状态估计误差p是渐近稳定的。
证明:选择李雅普诺夫函数Vp(k)=tr((k)T(k)),其中tr表示为的迹。可以得到
Vp(k+1)=tr((k+1)T(k+1))=tr[(a-(k+1))T(a-(k+1))]=tr[aTa-2aT(k+1)+(k+1)T(k+1)](21)
对方程(21)的最后两项进行转换,第2项可以改写为
tr(-2aT(k+1))=tr[-2aT(k+1)]=tr[-2aT((k)-λ(k)ΔJa())]=tr[-2aT(k)+2λ(k)aTΔJa())](22)
第3项可以改写为
tr((k+1)T(k+1))=tr[((k)-λΔJa())T((k)-λ(k)ΔJa())]=tr[(k)T(k)-2λ(k)(k)TΔJa()+λ(k)2ΔJa()TΔJa()](23)
将(22)和(23)带入(21)得到:
Vp(k+1)=Vp(k)+tr[2λ(k)a(k)TΔJa()+λ2(k)Ja()TΔJa()](24)
其中,(24)最后一项可以展开为
tr[2λa(k)ΔJa()+λ2Ja()TΔJa()] =tr[-4λ(k)a(k)Tp(k+1)Θ(k)T+4λ2(k)Θ(k)p(k+1)Tn(k+1)Θ(k)T]=tr[-4λ(k)p(k+1)Tp(k+1)+4λ(k)2Θ(k)TΘ(k)p(k+1)Tp(k+1)]=tr[-2Θ(k)TΘ(k)p(k+1)Tp(k+1)+1Θ(k)TΘ(k)p(k+1)Tp(k+1)]≤-1βp(k+1)Tp(k+1)(25)
然后,式(25)可以重新表述为
Vp(k+1)-Vp(k)≤-1βp(k+1)Tp(k+1)(26)
基于式(26),可以得出Vp(k)是递减的。因此,参数估计误差a(k)是有界的,1)得证。基于式(26)还可推导出:
Vp(k+1)-Vp(0)≤-1β∑k+1i=1p(i)Tp(i)(27)
进一步
1β∑+SymboleB@i=1p(i)Tp(i)≤Vp(0)-limx→SymboleB@Vp(k)(28)
其中,式(28)表明1β∑+SymboleB@i=1p(i)Tp(i)是有上界的,因此,状态估计误差p是渐近稳定的,2)得证。
1.4 估计系统的Adaptive MPC设计
本文提出一种为估计系统(9)设计的Adaptive MPC策略,该策略结合了自适应更新定律(20)。设定(k+i|k)表示从时间k往后i步的预测状态,其中i=,…,Np。因此估计系统(9)的预测方程为
(k+i|k)=i(k)(k|k)+∑i-1j=0i-j-1(k)Bu(k+j|k)(29)
预测方程(29)可以表示为
(k)=(k)x(k)+(k)U(k)(30)
其中,
(k)=[(k+1|k),(k+2|k),…,(k+Np|k)]T
U(k)=[u(k|k),u(k+1|k),…,u(k+Np-1|k)]T
(k)=(k)2(k)Np(k), (k)=B0…0(k)BB…0…Np-1(k)BNp-2(k)B…B
目标函数可以通过式(31)计算
J(k)=X(k)TQX(k)+U(k)TRU(k)=(k)TQ(k)+X(k)TQX(k)+2X(k)TQ(k)+U(k)TRU(k)≤2(k)TQ(k)+2X(k)TQX(k)+U(k)TRU(k)(31)
基于式(31),定义目标函数(k):
(k)=2(k)TQ(k)+2X(k)TQX(k)+U(k)TRU(k)(32)
同样,可得到扩维系统(4)的预测方程:
x(k+i|k)=i(k)x(k)+∑i-1j=0i-j-1(k)Bu(k+j|k)+i-j-1(k)w(k+j|k)(33)
其中,w(k)=(k)x(k)是以扰动形式表示的参数不确定性误差。预测方程(33)可写成:
X(k)=(k)x(k)+(k)U(k)+(k)W(k)(34)
其中,
X(k)=[x(k+1|k),x(k+2|k),…,x(k+Np|k)]T
W(k)=[w(k|k),w(k+1|k),…,w(k+Np-1|k)]T
(k)=I0…0(k)II…0…Np-1(k)INp-2(k)I…I
基于(29)和(33),可得到
(k+i|k)=Ai(k)(k|k)+∑i-1j=0Ai-j-1(k)(k)(k+j|k)(35)
式(35)可重述为
X(k)=M(k|k)+Ω(k)(k)=Ω(k)(k)(36)
其中,
M=[A,A2,…,ANc]T, (k|k)=x(k|k)-(k|k)=0
Ω(k)=(k)0…0AA(k)(k)…0…ANp-1(k)(k)ANp-2(k)(k)…(k)
将(36)代入(32),得到:
(k)=2(k)T(Q+Ω(k)TQΩ(k))(k)+U(k)TRU(k)(37)
其中,根据引理1中参数估计误差a是有界的,可以得到Ω(k)是有界的。因此,定义Ω(k)的边界为Ω-≤Ω(k)≤。然后定义新的目标函数Jupper(k):
upper(k)=(k)T2(Q+(k)TQ(k))(k)+U(k)TRU(k)(38)
状态和控制约束(2)可重述为
X(k)∈U(k)∈(39)
最后,优化:
U*(k)=arg minU(k)upper(x(k),U(k))(40)
s.t.
(k)=(k)x(k)+(k)U(k)(41)
(k)+(k)∈(42)
X(k)∈(43)
U(k)∈(44)
(k+Np|k)=0(45)
本文提出的Adaptive MPC策略的详细流程如算法1所示。
算法1
Input:初始状态(0)=x(0),初始估计矩阵(0),控制和预测时域Np,惩罚矩阵,R和P。
1 for k=0,,… do
2 通过优化(40),计算 u(k)=[ 0,…,0]U*(k),并把控制u(k)作用到系统。
3 量测实际不确定系统的状态 x(k+1)。
4 计算估计系统(9)的估计状态 (k+1)。
5 使用自适应更新律(20)更新估计系统(9)中的(k+1),其中p(k+1)可由p(k+1)=xp(k+1)-(k)Θ(k)获取。
6 设定(k+1)=x(k+1)。
7 end for
2 闭环系统稳定性分析
估计系统(9)的预测方程(29)可重新表述为
(k+i+1|k)=A(k+i|k)+Bu(k+i|k)-(k+i|k)(46)
其中,扰动(k+i|k)=(k)(k+i|k)=[0,…,In×n]Ta(k)(k),(k)=[u(k-d)T,p(k)T]T,i=0,…,Np-1。定义扰动的不确定集为
: ‖(k+i|k)‖2≤Vp(k)‖(k+i|k)‖2(47)
引理2 考虑到估计系统(9),如果优化(48)
U*(k)=arg minU(k)∈maxW(k)∈upper(x(k),U(k),W(k))(48)
满足状态和控制约束(2),鲁棒约束(47)和终端约束(45)在初始时刻k=0是可行的,那么陈述成立:1)优化(40)满足(41)(45)是递归可行的。2)所提出的具有自适应更新律的Adaptive MPC闭环系统是渐近稳定的。
证明:1)假设优化(48)在初始时刻是可行的,Vp(k)是固定的。那么,在k+1时刻,优化(48)的一组可行解如式(49)所示:
U(k+1)=[u(k+1|k+1),…,u(k+Np-1|k+1)u(k+Np|k+1)]T=[u*(k+1|k),…,u*(k+Np-1|k),u*(k+Np|k)]T(49)
进一步
w(k+i+1|k+1)=w*(k+i+1|k), i=0,…,Np-1
(k+i|k+1)=*(k+i|k), i= …,Np
其中
u(k+Np|k+1)=0(k+Np+1|k+1)=0w(k+Np|k+1)=0
基于以上分析可以得到,在k+1时刻优化(48)同样满足所有约束条件,因此优化(48)是递归可行的。
然而,上述结论假设Vp(k)是固定的,但现实情况Vp(k)是非增的,这意味着Vp(k+1)≤Vp(k)且(k+i|k)是非增的。因此,可以得到‖(k+i|k)‖≤‖w*(k+i|k)‖,那么一定存在另一组可行解U*优于(49)。优化(48)在k+1时刻是可行的,可以得到优化(40)在k+1时刻也是可行的,1)得证。
2)假设式(47)中Vp是固定的,考虑到优化(48)中的目标函数upper在k+1时刻为
upper(k+1)=∑Npi=1‖(k+i+1|k+1)‖2c+‖u(k+i|k+1)‖2Rc
=∑Npi=2[‖*(k+i|k)‖2c+‖u*(k+i-1|k)‖2Rc]+‖(k+Nc+1|k+1)‖2c+‖u(k+Nc|k+1)‖2Rc
=∑Npi=2‖*(k+i|k)‖2c+‖u*(k+i-1|k)‖2Rc
≤∑Npi=1‖*(k+i|k)‖2c+‖u*(k+i-1|k)‖2Rc=*upper(k)
得到
*upper(k+1)≤upper(k+1)≤*upper(k)
选择李雅普诺夫函数V(k)=‖(k|k)‖2c+*upper(k),令ΔV(k+1)=V(k+1)-V(k),得到
ΔV(k+1)=‖(k+1|k+1)‖2c+*upper(k+1)-‖(k|k)‖2c-*upper(k)=-‖(k|k)‖2c-‖u(k|k)‖2Rc≤-‖(k|k)‖2c
上式表明V(k)是递减的并且收敛于零。
由于在控制系统设计中结合了自适应更新律(20),这表明Vp(k)是随时间递减的,(k+i|k)也是递减的。因此,存在控制输入u优于u*,使得‖(k)‖2c+upper(k)≤V(k),可以得到(k)收敛于零。在定理1中已经证明了是渐进稳定的,根据x(k)=(k)+(k),可以进一步得到x(k)也是渐进稳定的,由此,2)得证。
3 数值计算
本文将进行数值计算来验证提出的Adaptive MPC策略的有效性。为了探讨系统在不同输入延迟步长下的控制表现,考虑到具有输入延迟和不确定性参数的约束系统,其动态可以建模为
xp(k+1)=0.248 5-1.035 50.891 00.406 5 xp(k)+0.319-1.308u(k-d)(50)
其中,d=,3,4。式(50)中Ap和Bp是未知,它们的名义参数是已知的,如式(51)所示。
p(0)=0.4-1.21.10.2 p(0)=0.42-1.4(51)
由于系统(50)具有输入延迟,需要用一种扩维表示法来转换系统(50),以在状态空间描述中表示延迟效应,参考式(4)。本例中,设置的参数为:状态初始值xp(0)=[3,2],预测时域和控制时域Np=10,控制约束‖u‖≤2,状态约束|Cx|≤4,其中,C=[ 0],权重矩阵Qc=diag[0. 0.1],R=diag[ 1],采样间隔h=0.1。
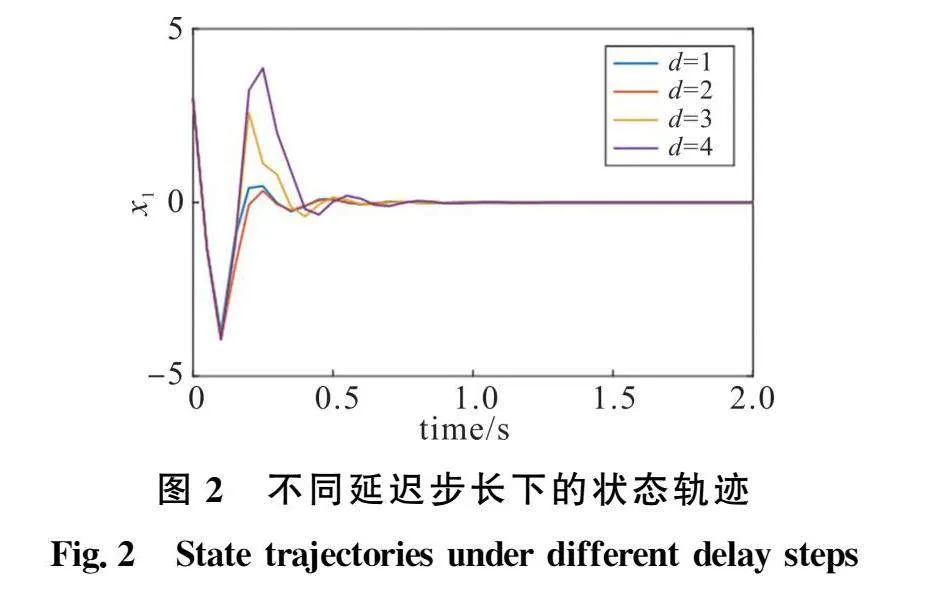
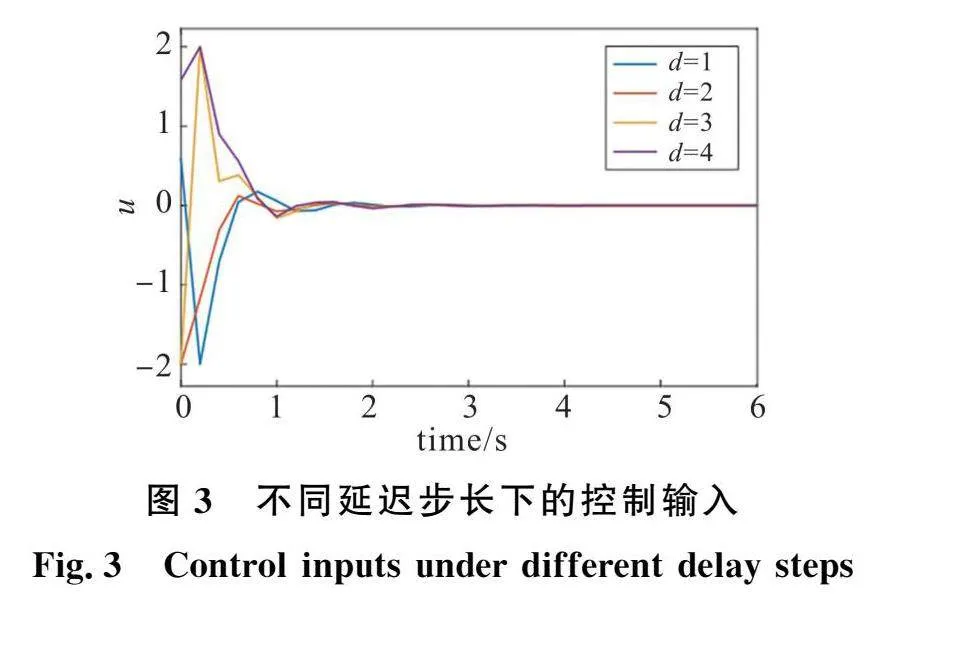
图2和图3比较了系统在不同输入延迟步长下的性能表现。从图2可以看到,本文提出的Adaptive MPC策略在4种延迟步长下都可以让闭环系统稳定,从图3可以看到不同延迟步长下的控制输入最终收敛于零并且满足约束,由此证明本文提出的方法是有效的。
4 结论
本文对含不确定参数和输入延迟系统的Adaptive MPC进行了详细分析。将研究扩展到同时含参数不确定性和输入延迟的约束系统,并获得了优化问题的数值解。此外,提出了一种时变的自适应更新律,它可以在系统有输入延迟的情况下更新估计系统的参数,并且证明了参数估计误差是有界的和状态估计误差是渐进稳定的。仿真结果表明了本文所提算法的有效性。
参考文献:
[1]GARCIA C E, PRETT D M, MORARI M. Model predictive control: theory and practice—a survey[J]. Automatica, 1989, 25(3):335348.
[2]LEE J H, MORARI M, et al. State-space interpretation of model predictive control[J]. Automatica, 1994, 30(4):707717.
[3]MAYNE D Q, RAWLINGS J B, et al. Constrained model predictive control: stability and optimality[J]. Automatica, 2000, 36(6): 789814.
[4]INCREMONA G P, FERRARA A, et al. MPC for robot manipulators with integral sliding modes generation[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(3): 12991307.
[5]KUMAR A S, AHMAD Z. Model predictive control (MPC) and its current issues in chemical engineering[J]. Chemical Engineering Communications, 2012, 199(4): 472511.
[6]MANZOOR T, SUN Z, XIA Y, et al. MPC based compound flight control strategy for a ducted fan aircraft[J]. Aerospace Science and Technology, 2020, 107: 106264.
[7]ADETOL V, DEHAAN D, GUAY M. Adaptive model predictive control for constrained nonlinear systems[J]. Systems & Control Letters, 2009, 58(5): 320326.
[8]ZhANG K, SHI Y. Adaptive model predictive control for a class of constrained linear systems with parametric uncertainties[J]. Automatica, 2020, 117: 108974.
[9]KARIMSHOUSHTARI M, NOVARA C. Design of experiments for nonlinear system identification: a set membership approach[J]. Automatica, 2020, 119: 109036.
[10] TANASKOVIC M, FAGIANO L, SMITH R, et al. Adaptive receding horizon control for constrained MIMO systems[J]. Automatica, 2014, 50(12): 30193029.
[11] BUJARBARUAH M, ZHANG X, TANASKOVIC M, et al. Adaptive stochastic MPC under time-varying uncertainty[J]. IEEE Transactions on Automatic Control, 2020, 66(6): 28402845.
[12] LORENZEN M, CANNON M,AllGWER F. Robust MPC with recursive model update[J]. Automatica, 2019, 103: 461471.
[13] TANASKOVIC M, FAGIANO L, GLIGOROVSKI V. Adaptive model predictive control for linear time varying MIMO systems[J].Automatica, 2019, 105: 237245.
[14] AKPAN V A, HASSAPIS G D. Nonlinear model identification and adaptive model predictive control using neural networks[J]. ISA Transactions, 201 50(2): 177194.
[15] REESE B M, COLLINS JR E G. A graph search and neural network approach to adaptive nonlinear model predictive control[J]. Engineering Applications of Artificial Intelligence, 2016, 55: 250268.
[16] ZHU B, XIA X. Adaptive model predictive control for unconstrained discrete-time linear systems with parametric uncertainties[J]. IEEE Transactions on Automatic Control, 2015, 61(10): 31713176.
[17] ZHU B, ZHENG Z, XIA X. Constrained adaptive model-predictive control for a class of discrete-time linear systems with parabeXj/boKL/G/TRXgZgknw==ametric uncertainties[J]. IEEE Transactions on Automatic Control, 2019, 65(5): 22232229.
[18] DHAR A, BHASIN S. Novel adaptivempc design for uncertain mimo discrete-time lti systems with input constraints[C]//2018 17th European Control Conference (ECC). Limassol, Gyprus: IEEE, 2018: 319324.
[19] DHAR A, BHASIN S. Indirect adaptivempc for discrete-time lti systems with parametric uncertainties[J]. IEEE Transactions on Automatic Control, 202 66(11): 54985505.
[20] HU Y, GOU L, FAN D, et al. An adaptive model predictive control strategy for a class of discrete-time linear systems with parametric uncertainty[J]. International Journal of Adaptive Control and Signal Processing, 202 35(12): 23892405.
(责任编辑 耿金花)

