交通流频变路段智能网联车辆换道演化博弈机制

摘要： 为研究城市交通流频变路段智能网联车辆换道博弈的演化机制和降低车辆换道的决策冲突，通过量化车辆收益和权重系数实现人车交互并建立演化动态方程，根据博弈系统的雅可比矩阵分析均衡点的稳定性，最后利用数值仿真决策演化路径并对影响因素进行灵敏度分析。结果表明不同驾驶决策的初始比例会影响决策的演化方向，左转绿灯时间增进车辆策略向（换道，让行）方向演化，随决策时刻位置减小增进车辆策略向（换道，让行）方向演化。

关键词： 智能网联车辆；交通流频变路段；强制换道；演化博弈

中图分类号： U491；U491.2文献标识码： A

Evolutionary Game Mechanisms of Lane Changing for Intelligent Connected Vehicles on Traffic Flow Frequently Changing Sections

DAI Shouchen， QU Dayi， MENG Yiming， YANG Yufeng，WANG Qikun

（School of Mechanical and Automotive Engineering， Qingdao University of Technology， Qingdao 266520，China）

Abstract：In order to study the evolutionary mechanism of lane changing for intelligent connected vehicles on urban traffic flow frequently changing sections and reduce the decision conflict of vehicle lane changing， the human-vehicle interaction was realized and the evolutionary dynamic equations were established by quantifying the vehicle revenue and weight coefficient. According to the Jacobi matrix of the game system， the stability of the equilibrium points were analyzed. Finally， the numerical simulation was used to determine the evolution path and the sensitivity analysis of the influencing factors was carried out. The results show that the initial ratio of different driving decisions will affect the evolution direction of the decision， and the left-turn green time will enhance the evolution of vehicle strategy in the direction of changing lane and giving way， and the evolution of vehicle strategy in the direction of changing lane and giving way as the position of decision time decreases.

Keywords： intelligent connected vehicles; traffic flow frequently changing sections; forced lane change; evolutionary game

0 引言

随着新能源汽车的生产和普及以及新能源汽车依托于不断发展的辅助驾驶或无人驾驶技术，未来的城市道路将出现一定规模的智能网联车辆行驶的交通场景。城市道路为人们驾车出行的主要场景，车辆换道是交通流中一种常见的车辆微观驾驶行为，因此，车辆的换道决策和交互行为成为交通流领域研究的热点。

城市路段的车辆换道特性主要在于车辆行驶受到信号灯的影响，相比于其他换道行为，信号灯等道路信息是交叉口换道模型中不可缺少的研究要素。丁建勋等［1］基于二维最优速度模型建立了信号交叉口的车辆跟驰换道模型，刻画了临近交叉口路段交通流的宏观特征；成卫等［2］基于元胞自动机研究了换道行为对交叉口路段交通流稳定性的影响，结果表明交通密度随绿信比增大而降低；Zhou等［3］基于强化学习模型，通过获取信号灯状况和行驶需求实现车辆的高效驾驶策略。此外，也有学者基于网联车辆的发展前景来研究复杂交通环境下的交叉口换道过程，杨达等［4］通过考虑信号灯和周围车辆的行驶状况建立了智能网联汽车的决策行为框架，结果表明综合环境信息后的车辆决策准确性得到显著提高。宗芳等［5］基于风险场理论刻画了网联环境下的行车风险状况，通过动态轨迹优化和速度控制提高了交叉口的行车效率。相较于上述模型侧重于刻画宏观交通流或提高交叉口通行效率，部分学者将车辆的交互过程作为重点进行研究，进而得到更为动态的微观换道模型。叶颖俊等［6］基于轨迹数据挖掘发现快速路汇入路段存在车辆试探后车回应式交互行为，从而拓展了传统的匝道车辆汇入模型。Zhang等［7］基于系统相似性分析和相互作用势理论，通过分子动力学刻画了车辆换道过程中的态势分布和交互关系。

随着博弈理论与交通领域的交叉发展，学者们将博弈论应用于车辆换道的研究中，将决策行为量化成相应的收益得失并通过求得最优解为车辆提供决策诱导，张可琨等［8］通过量化换道决策行为，基于换道碰撞概率建立了自动驾驶车辆博弈换道的决策模型；Guo等［9］通过将多主体博弈过程分解成子博弈系统建立了博弈论分解算法，结果表明所建模型可以降低计算复杂度并在交通拥堵情况下具有明显优势；Qu等［10］通过量化换道意图和换道动态风险研究了自动驾驶车辆的换道影响因素。

博弈理论的应用拓展了传统的换道规则模型，按照博弈顺序或持续时间又可以划分为动态和静态博弈，其中动态博弈相较于上述模型更能准确刻画驾驶员的交互过程，Shao等［11］基于信号博弈方法研究了不同交通密度下的换道成功率，通过灵敏度分析验证了模型稳定性；Ladino等［12］提出了一种高速匝道合并路段的动态博弈最优控制框架，刻画了车辆协同换道过程中的交互关系。肖雪等［13］采用主从博弈的方法描述了智能驾驶车辆的换道过程，通过量化代价函数建立了车辆换道决策及轨迹规划模型；禹乐文等［14］通过构建车辆侵入系数建立了复杂环境下的多人动态博弈模型，结果表明车辆博弈过程能在复杂环境中寻找最优策略和轨迹路线。随着对博弈决策的深入研究，部分学者通过研究其他场景提高了博弈换道模型的适用性。Zhang等［15］通过分析换道意图和视觉特征研究了雾天环境下的换道博弈模型，为复杂天气环境下的换道模型提供了参考。Peng等［16］提出了一种网联驾驶车辆协同决策方法，通过形成博弈联盟解决无信号交叉口的驾驶冲突，结果表明该决策算法可以提高无信号交叉口的通行效率和社会效益。

综上所述，学者们基于博弈理论对车辆换道进行了大量研究，但研究场景主要面向高速公路或瓶颈路段且模型通常基于博弈论侧重于对决策控制过程进行优化，缺少对换道博弈机理的研究而直接将博弈结果应用于策略控制，因此具有一定的局限性。针对上述问题，本文通过演化博弈理论来研究非完全理性下的左转车辆强制换道行为，通过量化决策权重实现人车交互并建立车辆换道演化博弈模型，对车辆初始决策倾向和主要宏观因素进行灵敏度分析并探讨换道稳定策略的收敛情况，通过仿真演化路径研究分析车辆强制换道的博弈演化机制，为车辆博弈决策与控制的相关研究提供理论参考。

1 换道博弈行为

1.1 博弈场景

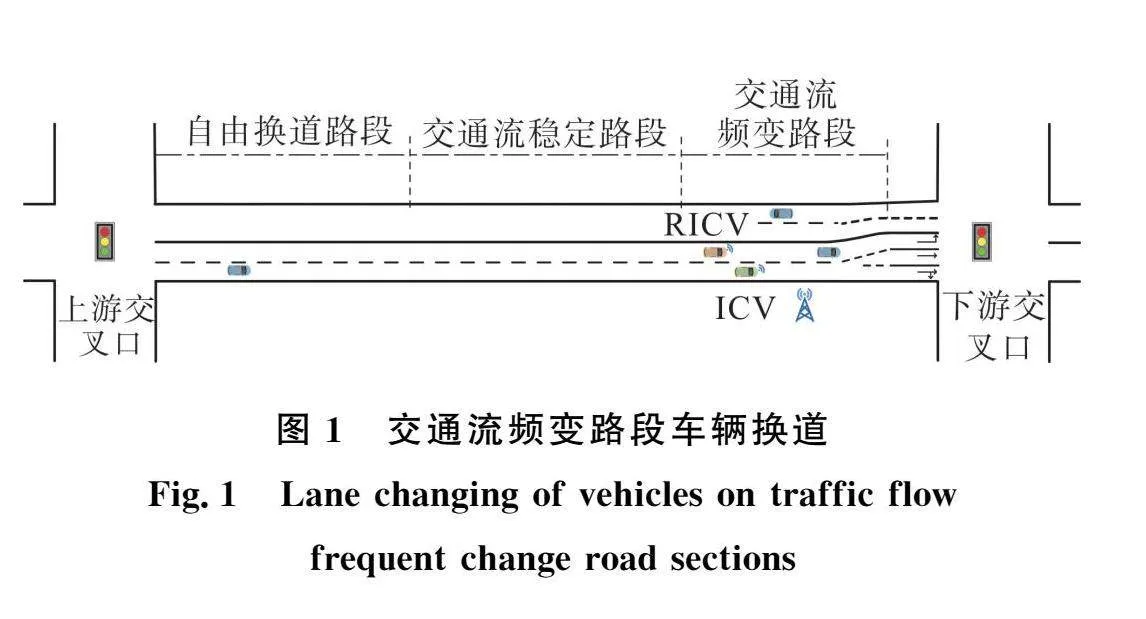
城市道路作为居民日常出行的主要场景承载了相当比例的车辆运行，而车辆换道作为道路交通中普遍的驾驶行为具有随行驶意图变化而变化的特点，车辆换道通常可以划分为自由换道和强制换道，二者频繁发生在城市道路的不同场景中。如图1所示双向四车道的城市路段中，各相邻交叉口之间的路段根据交通流的换道特性可以划分为自由换道、交通流稳定路段和交通流频变路段。

自由换道路段以上游交叉口出口道为起点，由于车辆性能和驾驶员操作的差异造成车辆起步和行驶速度不同，该路段上的车辆普遍追求较高的行驶速度，根据换道意图从而产生以自由换道为主的换道行为。当车辆在自由换道路段行驶并换道至期望车道时，车辆的行驶速度和车间距均满足驾驶员对行驶效率和安全的需求，因此，车辆通常以不同间距的车队或车辆簇的形式在一定长度的路段内稳定行驶，使得该路段的换道频率降低，呈现出交通流局部稳定的局面。对于人工驾驶车辆而言，由于驾驶员驾驶技术的不同，随着车辆驶近下游交叉口以及车辆驶入交通流频变路段时，保守的驾驶员更倾向于提前换道至目标车道并保持车道行驶，而对驾驶技术较为自信的驾驶员更倾向于选择车速较高的车道行驶。对于网联驾驶车辆而言，从人工驾驶环境转变为网联驾驶环境的过程中，网联驾驶车辆应遵循传统交通环境下的行驶特性以保障乘客的可接受性，网联驾驶车辆在满足乘客的乘坐期望的要求上还要遵守交通规则和促进维护良性的交通环境，因此，假定网联驾驶车辆不存在临近进口道时采取换道的激进驾驶行为，车辆为遵守交通规则均需要提前驶入目标车道行驶，交通流频变路段的车辆受制于道路和交通条件，车辆换道采取以强制换道为主的换道行为。

ICV（Intelligent Connected Vehicle）为换道车辆，RICV（Rear Intelligent Connected Vehicle）为目标车道后方车辆，本文界定模型场景为：假设周围车辆均在下游交叉口绿灯相位内以稳定状态行驶，ICV是行驶在右侧车道且需要左转的车辆，RICV是正常行驶在最左侧车道且同样需要左转的车辆，因此，ICV需要换道至最左侧车道完成左转任务。ICV采取向目标车道换道的行为通常受到RICV的影响，车辆的决策选择有换道和不换道，目标车道后车的决策选择有让行和不让行，当两车间距小于ICV以当前状态换道所需要的距离时，ICV需要RICV减速协助完成换道过程，由于RICV减速是对自身效率收益的损失策略而换道行为是ICV的增益策略，因此车辆之间需要进行换道博弈。

1.2 智能网联车辆功能界定

本文模型中的车辆均界定为智能网联车辆，车辆均搭载车载检测器、传感器等装置，车辆与路侧单元设施之间实现信息交互，包括车间距、车速等行驶状态信息，路侧单元设施也能获取道路设施如信号灯的状态信息，包括信号灯相位、剩余或下一绿灯时间等信息。相较于人工或混合交通环境，网联驾驶车辆之间可通过博弈控制系统完成博弈和决策过程，车辆通过车载设备获取车辆行驶状态并将状态信息发送至路侧信息接收端，博弈系统决策模块为博弈主体车辆确定离散化的驾驶目标，设定决策收益并通过博弈系统完成博弈演化过程，最终由路侧信息发送端为车辆提供稳定性驾驶策略，假设智能网联车辆均按照最优博弈策略做出相应行为，从而实现车辆换道决策控制过程。

智能网联车辆与乘客之间也具有一定的交互关系，车辆在做出决策行为时应考虑到一般乘客的决策期望，网联驾驶车辆在面对一定的交通环境时应当做出类人化的驾驶行为，车辆行驶属性如激进或保守能够随驾驶环境变化而变化，从而提高决策行为的合理性和乘客的可接受性。为简化博弈行为和决策过程，本文将智能网联车辆的驾驶任务离散化，车辆在某一时间段的行驶任务随交通环境变化而触发，并通过量化收益权重建立乘客期望车辆决策的人车交互机制，本文所建车辆博弈模型不考虑全局最优，通过博弈演化动态过程探究交通环境等因素对车辆换道决策的影响。

2 换道博弈行为模型

2.1 决策收益

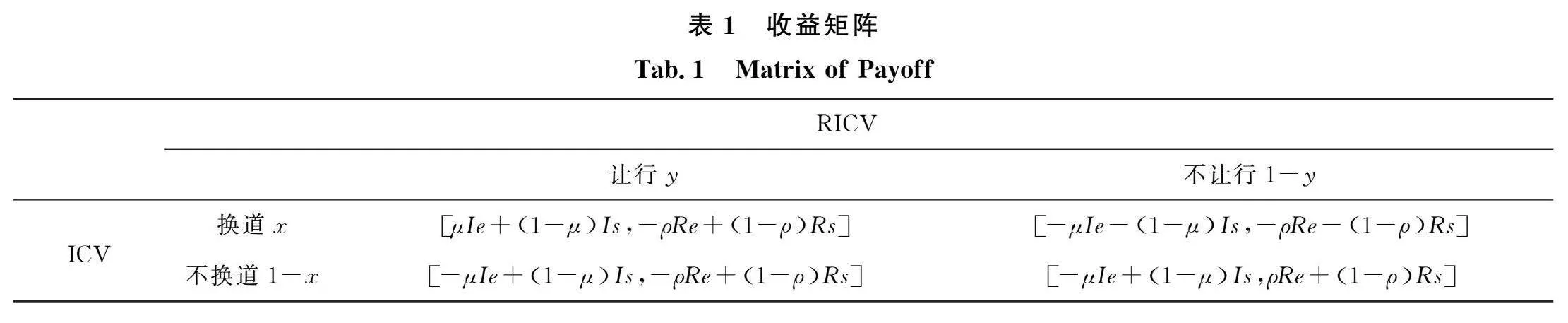
以上述场景中的ICV和RICV车辆为例分析车辆采取不同决策所对应的收益函数。当车辆间距不满足ICV换道要求时需要RICV协助做出减速决策，ICV与RICV的决策存在收益冲突而构成博弈场景，构建ICV和RICV的换道博弈收益函数分别为

I=μIe+1-μIs R=ρRe+1-ρRs（1）

其中，Ie和Is分别为ICV的效率收益和安全收益；Re和Rs分别为RICV的效率收益和安全收益；μ和ρ分别为各自的效率权重系数。

ICV和RICV的安全收益受到车辆间距和换道需求距离的影响，将二者的安全收益表示为

Is=Rs=ΔL-LminLmax-Lmin（2）

其中，ΔL为纵向车间距；Lmax为需要博弈换道的最大车间距；Lmin为后车协助减速可以完成换道的最小车间距。

基于目前自动驾驶车辆局部路径驾驶行为通常由场景触发，本文将车辆的驾驶任务离散化，ICV的驾驶任务为与目标车道后车进行博弈并换道至目标车道。RICV为在当前车道正常行驶而受到ICV换道期望影响的车辆，RICV采取让行或不让行决策将影响自身的效率收益。假设交通流稳定行驶，当ICV换道至目标车道时，通常会增加排队长度从而增加RICV的行程时间，当ICV未换道至RICV前方时，RICV的行程时间受博弈过程影响较小。因此，将ICV和RICV的效率收益分别表示为

Ie=ti-tImintImax-tIminRe=tr-tRmintRmax-tRmin（3）

其中，ti为ICV做出不同决策后所对应的换道时间；tImax、tImin分别为考虑车辆换道过程的最长和最短时间。tr为RICV采取不同决策所对应通过停车线的时间，tRmax、tRmin分别为RICV仅考虑与ICV博弈过程影响下由博弈时刻至通过停车线的最长和最短行程时间，最短行程时间为车流在期望车速下稳定行驶通过停车线所需时间。

由于本文界定了智能网联车辆的行驶场景和驾驶功能，智能网联车辆通过自动驾驶系统控制行驶，驾驶员由驾驶车辆改变为乘坐车辆，其身份由驾驶员转变为车辆乘客。智能网联车联在遵守交通规则的条件下需要兼容不同驾驶风格的乘客以期达到乘客的乘车期望，因此，智能网联车辆应建立与乘客的交互关系，设定车辆可以根据交通环境调整对效率和安全的收益权重，从而反映乘客对车辆决策的期望。考虑到智能网联车辆发展的前瞻性，本文不再考虑驾驶员风格的差异性，转而为智能网联车辆建立通用权重函数，对权重设置上下限以避免智能网联车辆过于片面追求安全或效率。

ICV换道需要考虑决策时刻位置和换道时间的影响，决策时刻位置越靠近停车线越倾向于完成车辆换道过程。RICV采取不同决策和左转绿灯时间会影响其行驶至交叉口的时间，且左转绿灯时间越短RICV越倾向于追求效率收益。因此，将ICV和RICV收益函数的权重分别表示为

μ=maxminSmax-SSmax-Smin+η，0.7，0.3ρ=minmaxtR-tGmintG-tGmin+η，0.3，0.7（4）

其中，S为ICV决策时刻至停车线的距离；Smin为ICV距交叉口停车线的最小期望换道距离，设置该值以维护良性的交通环境并减少实线区附近的换道冲突；Smax为交通流频变路段最远换道位置；tR为RICV采取不同决策对应的由当前位置至行驶过停车线的时间；tG为下游交叉口的左转绿灯剩余时间；tGmin为车辆由当前位置通过交叉口所需的最小绿灯时间；η为非零较小值。

通过分析决策冲突和构建收益函数建立如表1所示的收益矩阵。

2.2 ICV决策演化动态方程

演化博弈论被广泛应用于研究车辆换道和社会科学［1720］等决策问题，其理论思想为适应性调整策略并通过不断演化使得博弈者选择收益高的策略，该过程通常被视为一个具有时间概念的演化过程，演化博弈论通过演化动态方程描述不同策略的演化趋势，因此，对ICV建立决策时间连续情况下的演化动态方程，ICV选择换道和不换道决策所对应的期望收益EI1、EI2分别为

EI1=2μIe+1-μIsy+-μIe-1-μIs（5）

EI2=-μIe+1-μIs（6）

ICV以概率x选择换道、以概率1-x选择不换道的期望收益EI为

EI=2μIe+1-μIsxy-21-μIsx-μIe+1-μIs（7）

根据式（5）和（7）可得ICV选择换道决策的演化动态方程FI为

FI=xt=xEI1-EI=2xμIe+1-μIsy-1-μIs-μIe+1-μIsxy+1-μIsx=2x1-xμIe+1-μIsy-1-μIs（8）

2.3 RICV决策演化动态方程

对RICV建立决策时间连续情况下的演化动态方程，RICV选择让行和不让行决策所对应的期望收益ER1、ER2分别为

ER1=-ρRe+1-ρRs（9）

ER2=-2ρRe+1-ρRsx+ρRe+1-ρRs（10）

RICV以概率y选择让行、以概率1-y选择不让行的期望收益ER为

ER=yER1+1-yER2=-2ρRey-2ρRe+1-ρRsx+2ρRe+1-ρRsxy+ρRe+1-ρRs（11）

根据式（9）和（11）可得RICV选择让行的演化动态方程FR为

FR=yt=yER1-ER=2y-ρRe+ρRe+1-ρRsx+ρRey-ρRe+1-ρRsxy=2y1-y-ρRe+ρRe+1-ρRsx（12）

3 演化策略稳定性分析

由于演化博弈论考虑到博弈方具有有限理性的特点，因此博弈方受到实际环境的影响通常通过动态调整决策概率来逐步达到稳定状态。因此，通过式（8）和（12）联立可得关于ICV选择换道比例x和RICV选择让行比例y的微分方程组：

xt=0yt=0 x，y∈0，1（13）

无论所建模型中的收益函数如何变化，求解式（13）微分方程组总可以得到的解为（0，0）、（0，1）、（ 0）、（ 1），微分方程组另有一组与收益函数有关的解（x*，y*）即（ρRe/（ρRe+（1-ρ）Rs），（1-μ）Is/（μIe+（1-μ）Is））。

所建模型中动态博弈系统的雅可比矩阵为

JIR=FIxFIyFRxFRy=21-2xμIe+1-μIsy-1-μIs2x1-xμIe+1-μIs2y1-yρRe+1-ρRs21-2y-ρRe+ρRe+1-ρRsx（14）

根据式（15）得到雅可比矩阵的行列式JIR和迹trJIR分别为

JIR=21-2xμIe+1-μIsy-1-μIs×21-2y-ρRe+ρRe+1-ρRsx-2y1-yρRe+1-ρRs×2x1-xμIe+1-μIs（15）

trJIR=21-2xμIe+1-μIsy-1-μIs+21-2y-ρRe+ρRe+1-ρRsx（16）

将式（13）求得的5个均衡解分别代入式（15）和（16），从而得到各均衡点行列式和迹的数值正负，计算结果如表2所示。

根据稳定性原理，当均衡点满足trJIR小于0且JIR大于0时，此均衡点对应为演化稳定策略，通过矩阵的行列式和迹来判断均衡点的稳定性，则上述各均衡点的稳定性如表3所示。

根据以上稳定性判定可以得到稳定均衡点有（0，0）和（ 1），其对应的稳定策略分别为（不换道，不让行）和（换道，让行），不稳定点为（0，1）和（ 0），其对应的策略分别为（不换道，让行）和（换道，不让行），ρRe/（ρRe+1-ρRs），1-μIs/（μIe+1-μIs）为鞍点，向（0，0）或（ 1）收敛方向不定。

4 灵敏度分析

4.1 参数标定

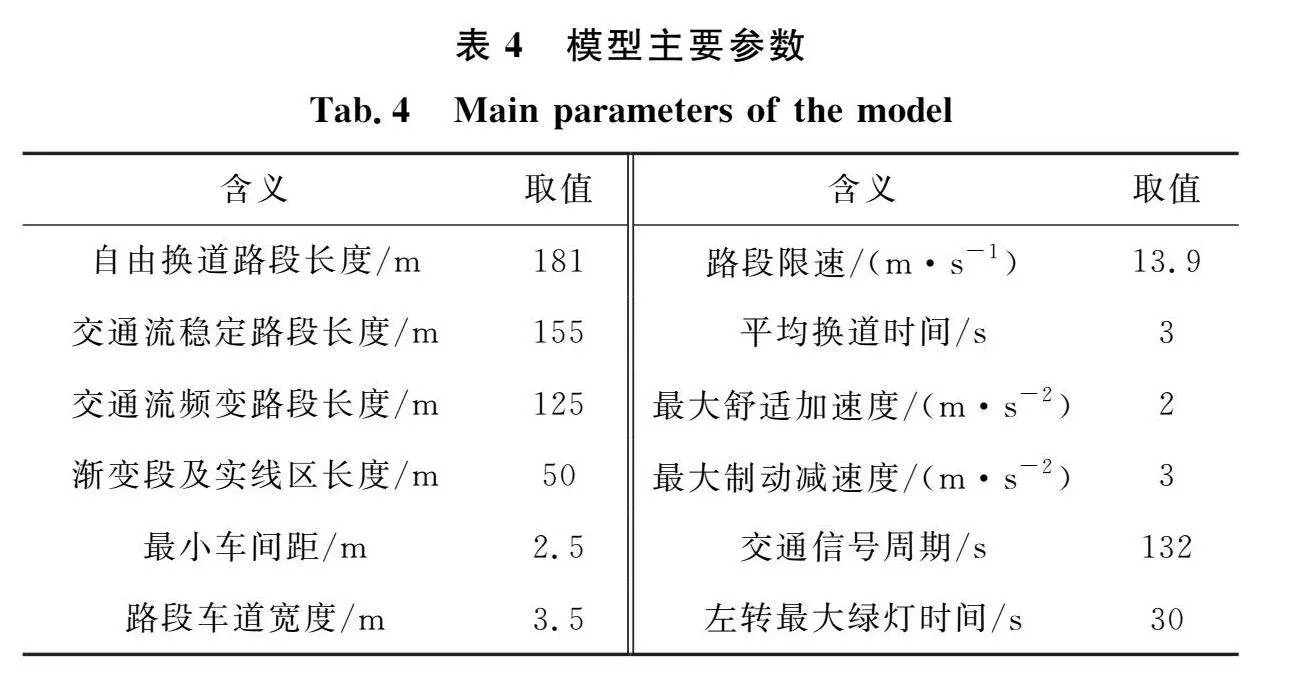
为详细阐明交通流频变路段智能网联车辆换道博弈的策略演化结果，选取青岛平度市人民路—永州路交叉口西向路段为调查地点、工作日平峰时段为调查时间，路段和交叉口渠化如图1所示，为路段双向四车道、进口道为三车道。采用视频检测和人工调查相结合方法对该路段的换道位置、平均速度和车间距等数据进行调查，通过对本文模型进行参数标定、构造换道收益函数并使用MATLAB对演化路径进行仿真，本文设定模型参数取值如表4所示。

4.2 初始决策倾向影响

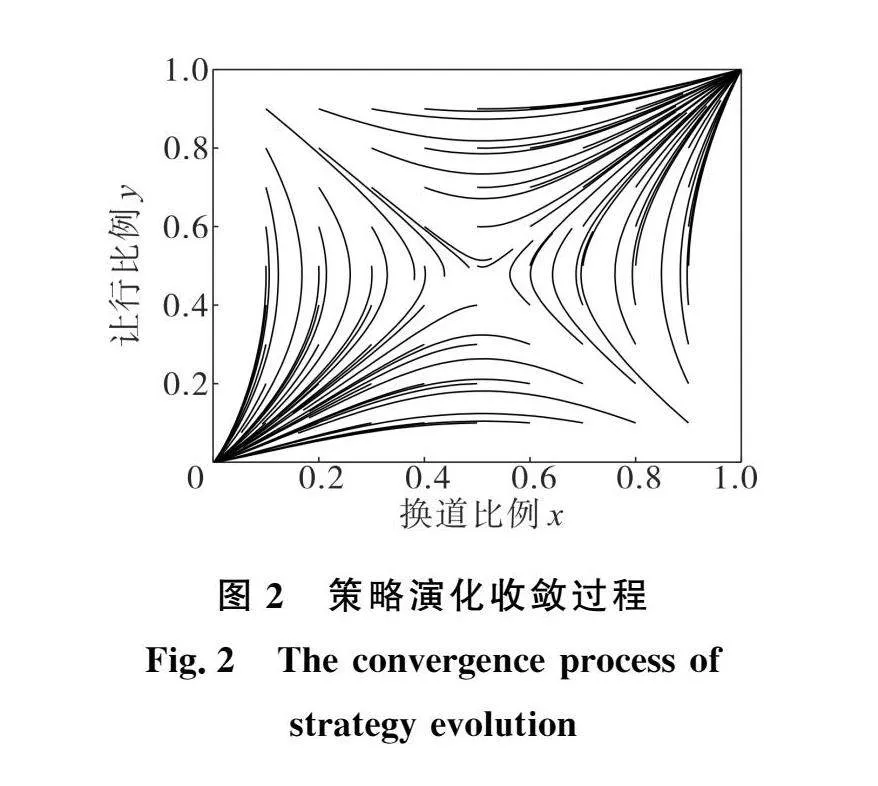
如图2所示为初始换道比例x和让行比例y分别以0.1的间隔在［0. 0.9］之间选取初始值得到的演化路径。当x和y初始值较小时，在演化路径中将收敛于不换道和不让行策略组合。当x和y初始值较大时，在演化路径中将收敛于换道和让行策略组合。

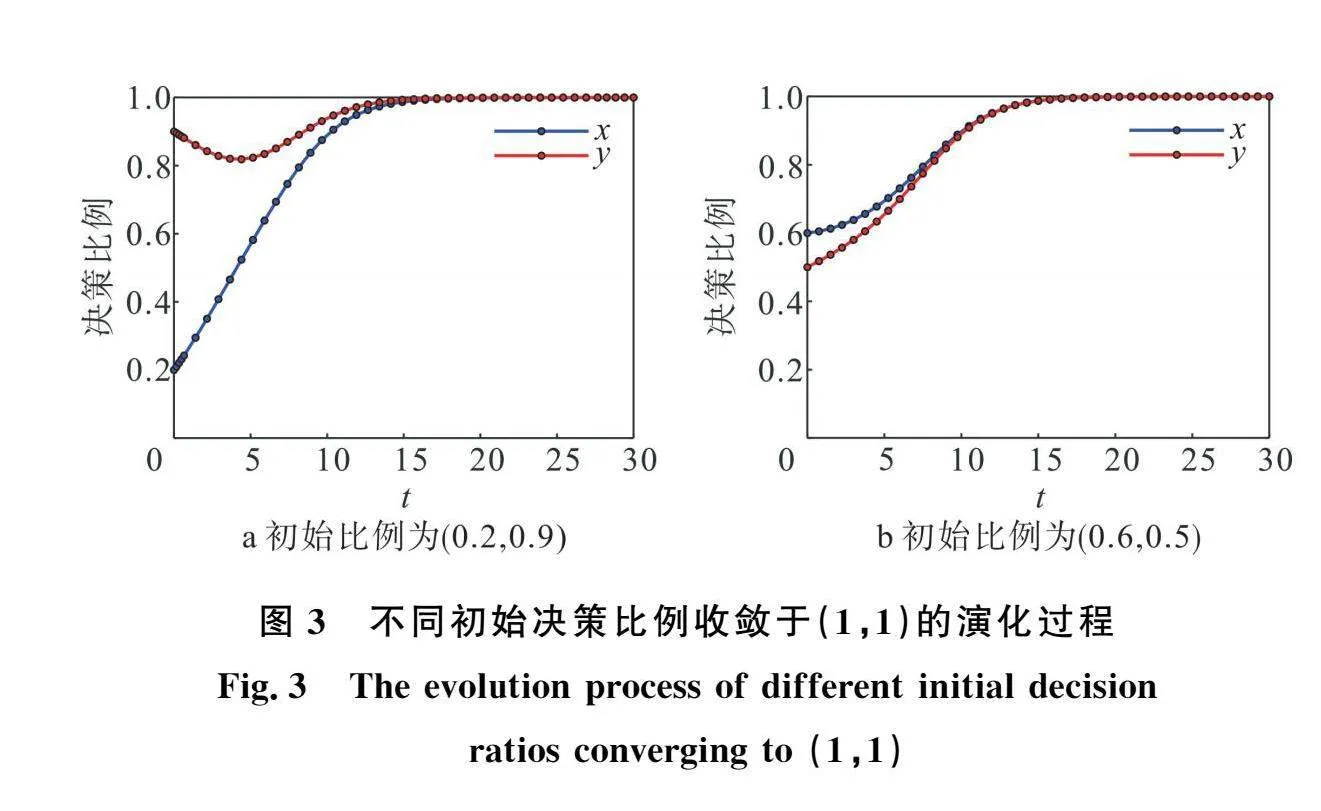
基于智能网联车辆的发展前景，未来的网联车辆可以在一定程度上体现乘客的行程需求和对车辆决策的可接受性。对于人工驾驶车辆而言，不同类型的驾驶员具有不同的初始决策倾向，因此，智能网联车辆可以通过量化权重系数实现乘客期望—车辆决策的人车交互机制，从而更好地兼容不同类型的乘客期望。如图3所示，以初始比例为（0.2，0.9）为例，即ICV初始决策倾向于不换道而RICV倾向于让行，根据收敛方向车辆策略向（ 1）点演化并最终收敛于（换道，让行）策略；当选取初始值为（0.6，0.5）时，即ICV初始决策倾向于换道而RICV相对中立，车辆策略向（ 1）点演化并最终收敛于（换道，让行）策略。

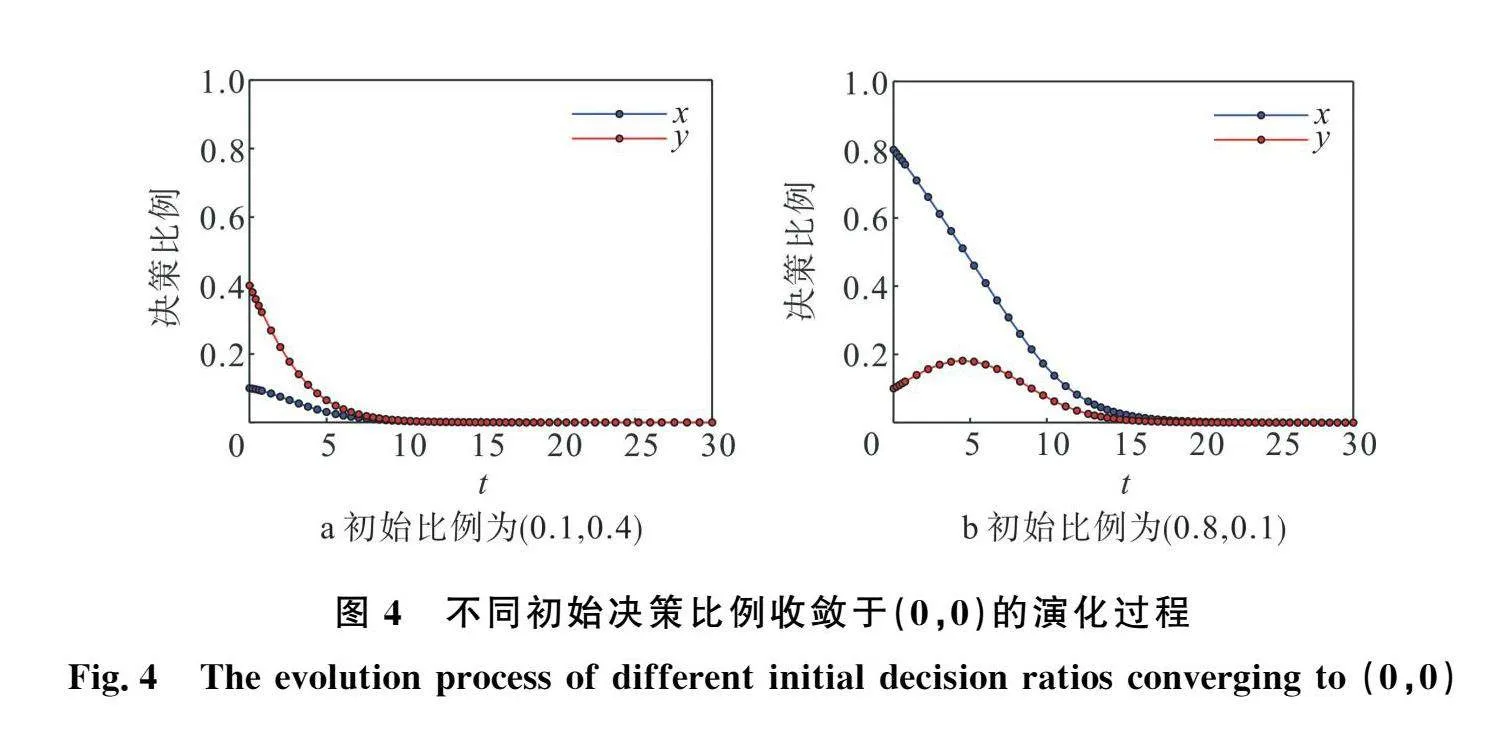
如图4所示，当选取初始比例为（0. 0.4）时，即ICV初始决策倾向于不换道而RICV倾向于不让行，车辆策略向（0，0）点演化并最终收敛于（不换道，不让行）策略；当选取初始值为（0.8，0.1）时，即ICV初始决策倾向于换道而RICV倾向于不让行，车辆策略向（0，0）点演化并最终收敛于（不换道，不让行）策略。

由于城市路段的交通流通常以信号交叉口的绿灯时间为时间分隔，因此车流呈现出以车辆簇的形式驶向下游交叉口，在上游交叉口不同绿灯相位内放行的车流中，不同车辆会表现出驾驶风格的差异性，对于智能网联车辆，车辆的决策倾向在一定程度上反应了乘客的决策期望，不同类型的乘客通过车辆决策获得可接受性的乘坐体验。此外，不同初始决策的影响与演化博弈论起源即在生物进化过程中不同物种之间进行竞争与合作有着相似之处，因此，当面对一定的交通环境时，被赋予不同驾驶期望的智能网联车辆在换道博弈中表现出不同的最优决策选择。

4.3 决策时刻位置影响

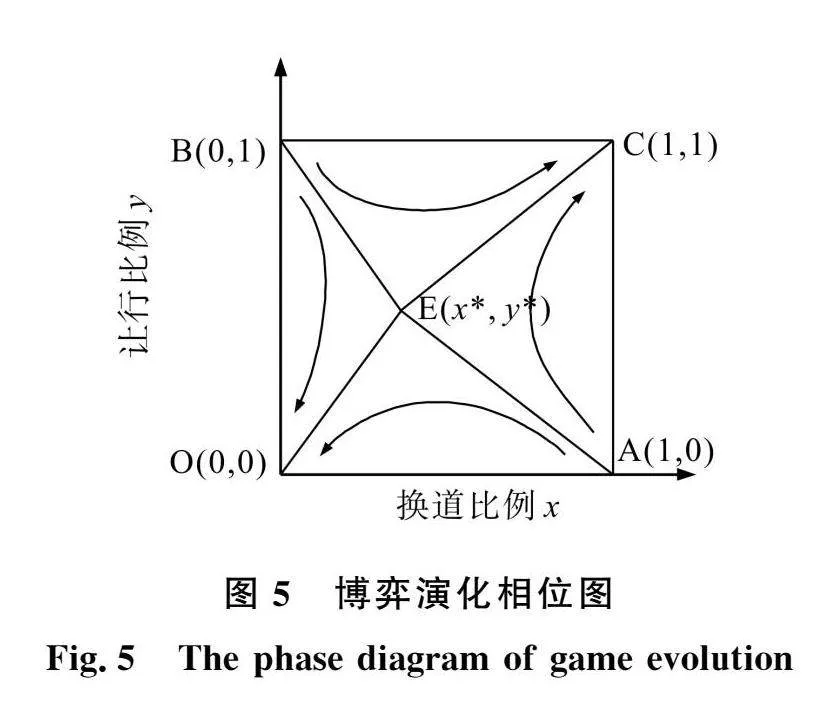
在演化博弈中，鞍点与初始决策比例的相对位置将影响不同策略的收敛方向，进而对演化的稳定策略产生影响，将式（13）所求均衡解划分为如图5所示相位图的A（ 0）、B（0，1）、C（ 1）、E（x*，y*）、O（0，0）5个点。将不同收敛区域的面积表示为

SAOBE=12［ρReρRe+1-ρRs+1-μIsμIe+1-μIs］（17）

SACBE=1-12［ρReρRe+1-ρRs+1-μIsμIe+1-μIs］（18）

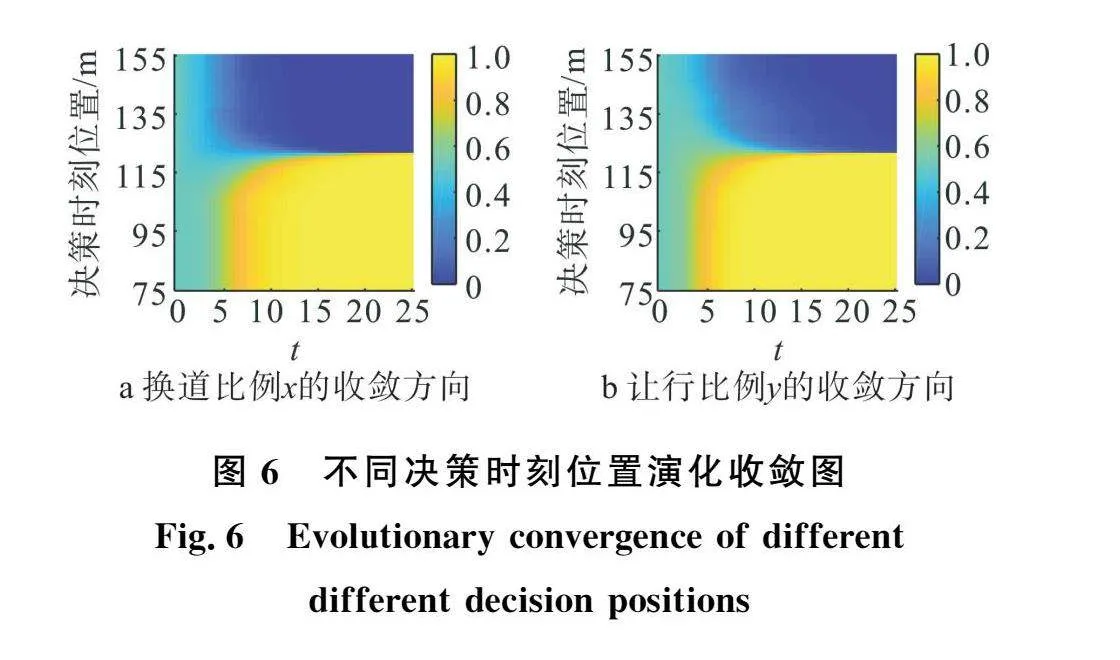
通过均衡解可知鞍点（x*，y*）的数值大小受收益函数和权重系数影响，因此，以博弈收益中的决策时刻车辆位置和左转绿灯时间为例进行灵敏度分析以研究宏观交通因素对博弈决策的影响。为降低上文所述初始值对决策演化的影响，在灵敏度分析过程中均将初始值设定为（0.5，0.5）并假定周围车流稳定行驶。调整决策时刻车辆位置的大小，并以1m为步长在（75，155）范围内进行变化，得到如图6所示的交通流频变路段车辆换道演化收敛随决策时刻位置的影响，S为车辆决策时刻ICV车头中心点距停车线的距离。

通过策略演化收敛情况可知随S增加，收敛于换道和让行的速度降低，收敛于不换道和不让行的速度加快，稳定点由 1向0，0改变，策略组合由（换道，让行）向（不换道，不让行）改变。其中，不同决策的临界值为119m，即S<119m时，博弈系统收敛于 1即（换道，让行），当S>119m时，系统收敛于0，0即（不换道，不让行）。

当车流行驶至交通流频变路段且下游交叉口左转绿灯剩余时间一定时，S数值越大使得RICV对于行驶效率的期望越大而ICV对换道效率的期望越小，x*、y*均向 1趋近使得SAOBE增大而SACBE减小，从而收敛于 1的初始值比例减少、收敛于0，0的初始值比例增加，因此，策略比例组合从收敛于 1向0，0改变。

4.4 左转绿灯时间影响

调整下游交叉口左转绿灯时间，并以1s为步长在（10，30）范围内进行变化，假设交通流稳定行驶并选定车辆决策位置为81 m，从而得到如图7所示的换道决策演化收敛随左转绿灯时间的影响，当决策时刻位置一定时，tG越大，收敛于换道和让行的速度越快，收敛于不换道和不让行的速度越低，稳定点由0，0向 1改变，策略组合由（不换道，不让行）向（换道，让行）改变。策略组合改变的临界值为14 s，即车辆行驶至某一位置且tG<14s时，博弈系统收敛于0，0即（不换道，不让行），当tG>14s时，系统收敛于 1即（换道，让行）。

当tG增加时，RICV对行驶至停车线的期望降低，鞍点向0，0点趋近使得SAOBE减小而SACBE增大，收敛于0，0的初始值比例降低而收敛于 1的比例增加，因此，策略组合向（换道，让行）策略收敛。

通过以上分析可以得出无论初始值如何选择，所建博弈系统中ICV和RICV的换道博弈均衡解最终将收敛于演化稳定点0，0或 1，即稳定策略组合收敛于（不换道，不让行）或（换道，让行）。网联驾驶车辆在做出决策行为时应考虑到乘客的决策期望，通过建立乘客期望—车辆决策交互关系，使得车辆在面对一定交通环境做出驾驶行为时能够考虑决策行为的合理性和乘客的可接受性。决策时刻位置和左转绿灯时间作为构成收益矩阵的组成因素对策略的选择具有影响作用，左转绿灯时间增进车辆决策向（换道，让行）方向演化，决策位置增进车辆决策向（不换道，不让行）方向演化，影响因素通过改变鞍点的位置进而改变不同收敛区域的面积以及鞍点与初始值的相对位置，从而改变初始值收敛方向进而影响稳定策略。

5 结论

本文研究了在城市交通流频变路段的车辆换道行为过程中左转强制换道车辆与目标车道后车对不同决策的演化博弈机制，通过数值仿真决策演化路径并以主要宏观因素为例进行了灵敏度分析，为车辆博弈决策与控制提供理论参考并得到结论：1）通过对均衡点的稳定性分析，该博弈系统有两种演化稳定策略即（换道，让行）和（不换道，不让行）、两种不稳定演化策略（换道，不让行）和（不换道，让行），最终演化方向通常受到交通环境的影响。2）通过量化收益权重建立乘客期望车辆决策的人车交互关系，决策收敛方向受到车辆初始策略倾向的影响并验证了智能网联车辆应具备体现乘客期望的必要性。3）通过量化博弈收益函数并通过灵敏度分析得出：随决策时刻车辆位置减小促使稳定策略向（换道，让行）演化，左转绿灯时间增加促使策略组合向（换道，让行）方向演化。根据本文模型可以探究车辆换道博弈的策略演化机制和智能网联车辆与乘客的交互关系，为智能网联车辆的博弈换道决策提供参考。但模型也具有一定的局限性，如对车辆决策控制过程和车辆动态交互行为的细节研究较为不足，后续研究还需考虑更加复杂的交通情况来完善车辆换道的决策演化和控制模型。

参考文献：

［1］丁建勋，郑杨边牧，张梦婷， 等.临近交叉口的车辆跟驰换道行为研究 ［J］. 交通运输系统工程与信息， 2017， 17（3）： 6066.

DING J X，ZHENG Y B M，ZHANG M T， et al. Car-following and lane-changing behaviors near an intersection ［J］. Journal of Transportation Systems Engineering and Information Technology， 2017， 17（3）： 6066.

［2］成卫，周通，李冰. 驾驶员变更车道对信号交叉口交通流的影响 ［J］. 昆明理工大学学报（自然科学版）， 202 46（3）： 149154.

CHENG W， ZHOU T， LI B. Influence of driver changing lane on traffic flow at signalized intersections ［J］. Journal of Kunming University of Science and Technology （Natural Sciences）， 202 46（3）： 149154.

［3］ZHOU M F，YU Y，QU X B. Development of an efficient driving strategy for connected and automated vehicles at signalized intersections： a reinforcement learning approach ［J］. IEEE Transactions on Intelligent Transportation Systems， 2020， 21（1）： 433443.

［4］杨达，杨果，罗旭， 等. 考虑前车状态的智能网联车交叉口行为决策 ［J］. 西南交通大学学报， 2022， 57（2）： 410417，433.

YANG D，YANG G，LUO X， et al. Behavior decision of intelligent connected vehicles considering status of preceding vehicles at intersections ［J］. Journal of Southwest Jiaotong University， 2022， 57（2）： 410417，433.

［5］宗芳，石蕊，刘怿轩， 等. 信号交叉口行车风险场建立及车辆通行行为优化 ［J］. 中国公路学报， 2022， 35（10）： 244253.

ZONG F，SHI R，LIU Z X， et al. Construction of risk field and optimization of driving behaviors for signalized intersections［J］. China Journal of Highway and Transport， 2022， 35（10）： 244253.

［6］叶颖俊，倪颖，孙剑. 高密度瓶颈交通流主动回应汇入行为定义与建模 ［J］. 中国公路学报， 2022， 35（8）： 278290.

YE Y J，NI Y，SUN J. Defining and modeling active-responsive merging behavior at high-density expressway on-ramp bottlenecks ［J］. China Journal of Highway and Transport， 2022， 35（8）： 278290.

［7］ ZHANG K K，QU D Y，SONG H， et al. Analysis of lane-changing decision-making behavior and molecular interaction potential modeling for connected and automated vehicles ［J］. Sustainability， 2022， 14（17）： 120.

［8］张可琨，曲大义，宋慧， 等. 自动驾驶车辆换道博弈策略分析及建模 ［J］. 复杂系统与复杂性科学， 2022， 12（7）： 110.

ZHANG K K，QU D Y，SONG H， et al. Analysis and modeling for lane-changing game strategy of autonomous vehicles ［J］. Complex Systems and Complexity Science， 2022， 12（7）： 110.

［9］GUO J，HARMATI I. Lane-changing decision modelling in congested traffic with a game theory-based decomposition algorithm ［J］. Engineering Applications of Artificial Intelligence， 2022， 107（5）： 10453050.

［10］QU D Y，ZHANG K K，SONG H， et al. Analysis and modeling of lane-changing game strategy for autonomous driving vehicles ［J］. IEEE Access， 2022， 10（2）： 6953142.

［11］SHAO H P，ZHANG M R，FENG T， et al. A discretionary lane-changing decision-making mechanism incorporating drivers’heterogeneity： a signalling game-based approach ［J］. Journal of Advanced Transportation， 2020， 10（16）： 116.

［12］LADINO A，WANG M. A dynamic game formulation for cooperative and change strategies at highway merges［J］. IFAC-PapersOnLine. 2020， 53（2）： 1505964.

［13］肖雪，李克平，彭博， 等. 基于决策规划迭代框架的智驾车换道行为建模 ［J］. 吉林大学学报（工学版）， 2023， 53（3）： 746757.

XIAO X，LI K P，PENG B， et al. Integrated lane-changing model of decision making and motion planning for autonomous vehicles［J］. Journal of Jilin University （Engineering Edition）， 2023， 53（3）： 746757.

［14］禹乐文，罗霞，刘仕焜. 复杂车路环境下自动驾驶车辆换道仿真研究 ［J］. 计算机仿真， 202 38（5）： 146152.

YU L W，LUO X，LIU S K. Research on simulation of lane-changing for autonomous vehicles under complex road conditions ［J］. Computer Simulation， 202 38（5）： 146152.

［15］ZHANG X G，GAO J P，LI L， et al. Expressway lane change in fog environment by dynamic strategic game ［J］. Journal of Advanced Transportation， 2022， 10（1）： 110.

［16］PENG H，HUANG C，HU X Z， et al. Decision making for connected automated vehicles at urban intersections considering social and individual benefits ［J］. IEEE Transactions on Intelligent Transportation Systems， 2022， 23： 2254956.

［17］杜筱婧，姚荣涵. 智能网联公交车出站强制换道的演化博弈机制 ［J］. 吉林大学学报（工学版）， 2024， 54（1）： 124135.

DU X J，YAO R H. Evolutionary game mechanism of mandatory lane changing for exiting for intelligent connected bus ［J］. Journal of Jilin University （Engineering Edition）， 2024， 54（1）： 124135.

［18］李超然，刘举胜，宋美，等， 演化博弈视角下的医患关系分析及对策研究 ［J］. 复杂系统与复杂性科学， 2022， 19（3）： 4454.

LI C R，LIU J S，SONG M， et al. Analysis of doctor-patient relationship and countermeasures from the perspective of evolutionary game ［J］. Complex Systems and Complexity Science， 2022， 19（3）： 4454.

［19］彭伟华，侯仁勇，李光红. 基于演化博弈的网络平台就业多元协同治理研究 ［J］. 复杂系统与复杂性科学， 2022， 19（2）： 916，30.

PENG W H，HOU R Y，LI G H. Research on multiple collaborative governance of network plaCungTJ3Muj8ERkCg6z9s248nG/pitOZCx8q+cVKtXCI=tform employment based on evolutionary game ［J］. Complex Systems and Complexity Science， 2022， 19（2）： 916，30.

［20］李春发，刘焕星，胡培培. 政府分类规制、智能平台赋能与药企CSR策略演化 ［J］. 复杂系统与复杂性科学， 2022， 19（2）： 1730.

LI C F，LIU H X，HU P P. Government classification regulation， intelligent platform empowerment and CSR strategy evolution of pharmaceutical enterprises ［J］. Complex Systems and Complexity Science， 2022， 19（2）： 1730.

（责任编辑 李 进）