基于改进蚁群算法的复杂环境路径规划

摘要： 针对蚁群算法在复杂环境下难以收敛、最优值差的问题，提出了一种改进蚁群算法。引入修正策略，提出两种局部修正方法以减少无效路径。提出一种自适应信息素更新机制，将初始信息素与蚂蚁所释放的信息素区分挥发；针对每次迭代蚂蚁所释放的信息素，通过设计时变挥发因子的变化律单独挥发，得到自适应挥发强度的信息素挥发机制。最后，将算法应用到不同复杂环境，与已有改进蚁群算法对比分析，研究结果说明改进算法在有效时间、平均距离、最短距离的优越性。

关键词： 蚁群算法；改进蚁群算法；全局优化；路径规划

中图分类号： TP18;TP29文献标识码： A

Complex Environment Path Planning Based on an Improved Ant Colony Algorithm

YANG Junqi， LIU Feiyang， ZHANG Hongwei

（School of Electrical Engineering and Automation， Henan Key Laboratory of Intelligent Detection and Control of Coal Mine Equipment， Henan Polytechnic University， Jiaozuo 454003， China）

Abstract：This paper proposes an improved ant colony algorithm to solve the problem of slow and poor convergence. First， a correction strategy is introduced， which includes two local correction methods to reduce invalid paths. Second， an adaptive pheromone updating mechanism is developed to distinguish and volatilize the initial pheromone from the pheromone released. For the pheromone released in each iteration， a change law of time-varying volatilization factor is designed to volatilize independently and obtain pheromone volatilization mechanism with adaptive volatilization intensity. Finally， the proposed algorithm is applied to mobile robot path planning. Compared with the existing improved ant colony algorithms， the results show that the improved algorithm is excellent in terms of effective time， average distance and shortest distance.

Keywords： ant colony algorithm; improved ant colony algorithm; global optimization; path planning

0 引言

蚁群算法是一种群体智能仿生算法［15］，具有并行处理、分布式计算、鲁棒性强等优点，主要解决路径规划问题以及NP难问题，但仍有收敛速度慢、易停滞、有可能陷入局部优化等缺点。为了提高算法性能，研究人员做了一些改进［620］。Hou等［6］扩大轮盘赌算法加速收敛，设计自适应S型衰减曲线优化启发函数。Tian等［9］采用多步搜索策略替代单步搜索策略，以提高算法性能。文献［1112］通过调整网络中的初始信息素含量，提升了算法的性能以及收敛速度。文献［13］设计了一种改进蚁群算法，将原有的二维平面搜索路线空间扩展到三维空间。文献［14］在蚁群算法中引入Q-Learning，使蚁群具有自学习能力，用以解决矩阵排样问题。文献［1718］从增强搜索能力的角度改进蚁群算法，提升了算法的收敛速度。

上述方法虽然性能有了改进，但对于复杂的环境模型仍会出现收敛慢、结果差的问题。如文献［15］，虽然增大了蚂蚁的视野、提高了算法的收敛结果，但对于更加复杂的环境，蚂蚁视野有限，难以跳出局部最优陷阱。文献［20］利用历史路径整合蚂蚁路径，达到蚂蚁间通信的目的，从而减少曲折路径。但上述结果对于更加复杂的环境，由于蚂蚁数量有限、历史路径不能覆盖整个环境模型，会出现难以收敛、最短路径结果不好的问题。本文基于文献［20］整合历史路径的思路，提出了一种修正策略，该策略能够修正蚂蚁路径，减少曲折路线信息素的干扰，最终提升算法收敛速度和收敛结果。此外，本文提出了一种自适应挥发强度的信息素挥发机制，增强了算法性能。修正策略修正曲折路线后，减少曲折路线对蚂蚁的干扰，增强算法的收敛速度。同时该路径上信息素浓度会增强，降低了蚂蚁的搜索性，而设计的信息素更新机制中挥发强度与信息素浓度正相关，解决了局部路径信息素浓度过高的问题。

针对蚁群算法复杂环境难以收敛的问题，引入修正策略和自适应挥发强度的信息素更新机制。主要工作包括：1）引入修正策略，解决蚂蚁路线曲折路径过多的问题；2）设计了一种全新的信息素更新机制，使得信息素挥发强度与信息素浓度正相关，增强算法鲁棒性和搜索能力；3）用改进蚁群算法解决复杂环境路径规划问题，并且与基本蚁群算法和文献［15］、［20］在不同复杂环境下对比分析，证明本文算法性能优秀。

1 问题描述

1.1 环境建模

多栅格地图法是对路径规划最普遍的方法。首先，对真实环境进行取样，膨胀化处理取样图形，使之占满整个栅格，令所有触碰到障碍物的栅格全部按照障碍物处理。如图1所示，环境空间被分割为两个部分，白色网格为可达空间，黑色网格为不可达空间。按照从左到右、从上到下的排序方式，对环境空间网格进行排序。此外，根据障碍物数量和大小可分割成不同维度的环境模型，节点状态转移方向若无障碍物，则8个方向均可达。如图2中的节点5，因节点6、8不可达，则节点9因障碍物遮挡不可达。

1.2 基本蚁群算法

假设m只蚂蚁在具有n节点的网络中寻找食物，根据状态转移概率公式选择前进路径。用Pij表示某只蚂蚁从节点i到节点j的转移概率，即

Pijt=τijtαηijtβ∑l∈allowediτiltαηiltβ， l∈allowedi0， lallowedi（1）

其中，allowedi为i节点下一步允许选择的节点集。α为信息素启发因子，β为启发函数启发因子，τijt为t时刻节点i到节点j的信息素浓度。考虑t时刻节点i到节点j的如下常量启发函数ηijt=ηij=1dij，其中dij表示节点i到节点j的欧式距离。记蚁群路径网络启发矩阵为η=ηij∈Rn×n。

蚂蚁完成一次循环后信息素浓度的更新规则：

τijt=1-ρτijt+Δτijt

其中，0<ρ<1为信息素挥发系数，1-ρ是信息素残留系数。记信息素矩阵τt=τijt∈Rn×n。Δτijt为节点i到节点j的信息素增加量，即所有M只蚂蚁经节点i到节点j释放的信息素之和，那么

Δτijt=∑Mk=1Δτkijt（2）

这里Δτkijt=QLkt为蚂蚁k释放的信息素，其中Q为信息素强度系数，Lkt为蚂蚁k所走路径的长度。

2 改进蚁群算法

2.1 引入修正策略

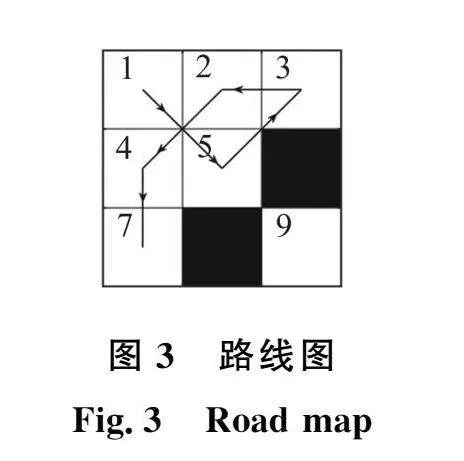
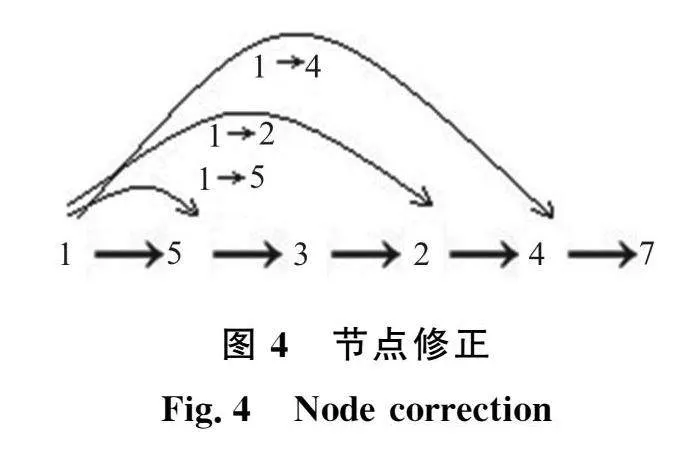
蚂蚁迭代中，因初期环境模型初始信息素浓度一致，导致式（1）中仅有启发信息对蚂蚁前进起指导作用。所以，在复杂环境中，初期蚂蚁路径会出现许多如图3所示的曲折路线，误导蚂蚁爬行，影响算法收敛。因此，本文引入修正策略能够修正曲折路径，加快蚂蚁在复杂环境收敛速度（见图4）。如图3所示的3×3环境模型中移动，初始地为1，目的地为78a98d07a5021a90d6a6776c7389e820fab0c0a1a69314278ba15794470f81253。某只蚂蚁在初次迭代搜索出的路径为1→5→3→2→4→7，此时最短路径为1→4→7，多行路径为5→3→2。

2.1.1 节点修正

设某只蚂蚁搜索到的路径节点表示为集合Θpath，pathn为该蚂蚁搜索到路径的节点n，该节点下一步可转移的节点集合为allowpathn，I表示Θpath与allowpathn交集后的集合，Li为I中的节点i与节点n在路径Θpath上的长度，即

I=Θpath∩allowpathn（3）

Li=length（i-n）（4）

其中，i为节点，且i∈I，length为计算节点i到节点pathn的长度。

给定路线图3和节点n=1修正策略示意图4，易知Θpath= 5，3，2，4，7和allowpathn=2，4，5，则由式（3）可得I=2，4，5。利用式（4）得L2≈3.828、L4≈5.242、L5≈1.414，易知L4为最大值，其所对应的节点为i=4，则节点1到节点4之间的路径长度最长。由于节点1可直接到达节点4，此时删除节点1～4之间的所有节点2，3，5，即完成对节点1的修正。

2.1.2 取直修正

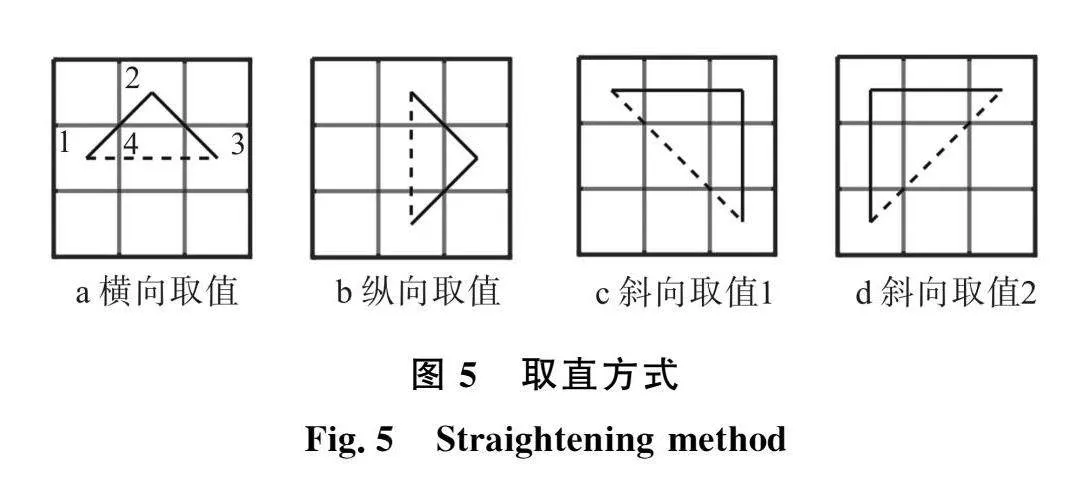
蚂蚁搜索出的路径因全局性能力不足，会导致路径中出现一些如图5所示的曲折路径。

为优化路径，以下提出一种取直修正策略。假设蚂蚁只能在横向、纵向、斜向的搜索方向爬行，以图5a为例，蚂蚁所搜路径中的某一段为123。显然，节点2是造成曲折路径的主要原因，若蚂蚁路径修正为143，则减少了路径的曲折路线。图5a中，13符合取直修正，若节点13连线之间存在障碍物，则13因障碍物遮挡不可直达，此时这两节点无法取直修正，选择其他节点继续进行修正策略。

2.2 修正策略的执行步骤

在改进算法的设计中，若对每一次迭代产生的路径都进行修正策略，则会花费较多时间。当蚁群算法收敛以后，则不必再进行路径修正，因此定义参数N0限定修正策略执行次数以降低算法时间。

改进算法入口参数为某只蚂蚁搜索路径Θpath和环境模型矩阵G，返回优化后的路径Θ′path。算法如下：

步骤1：初始化参数。计算矩阵G的邻接矩阵D，定义计数器c1=1、c2=3。

步骤2：while（1）循环，为节点修正。若c1小于路径Θpath长度，从邻接矩阵D中找出蚂蚁下一步可选择节点allowpath（c1）。由式（3）、（4）得Li、I，并得出imax使得Limax最大。从路径Θpath中删除c1-imax节点；若c1等于路径Θpath长度，令c1=1退出该循环，完成节点修正。

步骤3：while（1）循环，遍历节点X，为取直修正外层循环。若c1+2、c2皆等于路径Θpath长度，则退出该层循环。否则进入步骤4。

步骤4：while（1）循环，遍历节点Y，为取直修正内层循环。若c2等于路径Θpath长度，则令c1=c1+1进入步骤3；否则，进入步骤5。

步骤5：判断X、Y是否符合2.1.2小节中的取直方式。若不符合，则令c2=c2+1进入步骤4；若符合，则按照2.1.2小节修正Θpath，令c2=c1+2并进入步骤3。

步骤6：Θ′path=Θpath，结束算法。

2.3 修正策略效果

在30×30环境模型中，图6为某条路径修正示意图，虚线为未修正路径，实线为修正后路径。从图6中可以看出经修正后减少了许多曲折路线，从而降低了蚂蚁的爬行距离。如坐标0.5，29.5经节点修正后的路径为0.5，29.5-0.5，28.5，右侧虚线多行路径被修正，坐标9.5，13.5、12.5，12.5、13.5，12.5等同样为节点修正。在取直修正部分，坐标3.5，21.5和3.5，19.5符合图5b纵向取直，采用取直修正，坐标组合1.5，13.5与6.5，13.5、7.5，13.5与9.5，13.5等，都符合图5中的取直方式，因此用取直路径替代原路径。

2.4 自适应挥发强度的信息素更新机制

在基本蚁群算法中，信息素挥发因子ρ决定信息素留在一条路径上的时间和强度，合适的信息素挥发机制很大程度上影响蚂蚁的搜索效率，本文提出了一种自适应挥发强度的信息素更新机制。

定义初始信息素挥发为

σijt=1-ρσijt-1（5）

其中，t=，…，n，σij0为初始信息素值，σijt为初始信息素在第t次迭代时的值。记σt=σijt∈Rn×n为挥发后的初始信息素矩阵。蚂蚁所释放的信息素因子随迭代次数的变化律设计为

ρt=ε-t-t0+ρ0，t>00，t=0（6）

其中，ρ0和t0是常量参数，参数ε>1确保ρt是关于t的单调减函数。

在式（2）中，表示Δτt=Δτijt∈Rn×n，且随迭代次数而形成的信息素矩阵集定义为

Αt=Δτ Δτ2，Δτ3，…，Δτt。

对于任意给定Δτk∈At，结合（6）式给出t时刻信息素挥发公式：

ζk=1-ρt-kΔτk（7）

其中，ζk为挥发后的信息素矩阵。则挥发后信息素矩阵集为

Βt=ζ ζ2，ζ3，…，ζt

对于当前迭代时间t，依据式（2）、（5）和（7），构造如下全局信息素更新律：

τt=σt+∑t-1i=1ζi+Δτt

其中，σt为挥发后的初始信息素矩阵，∑t-1i=1ζi为挥发后蚂蚁释放的信息素矩阵之和，Δτt表示蚂蚁此次迭代释放的信息素矩阵。

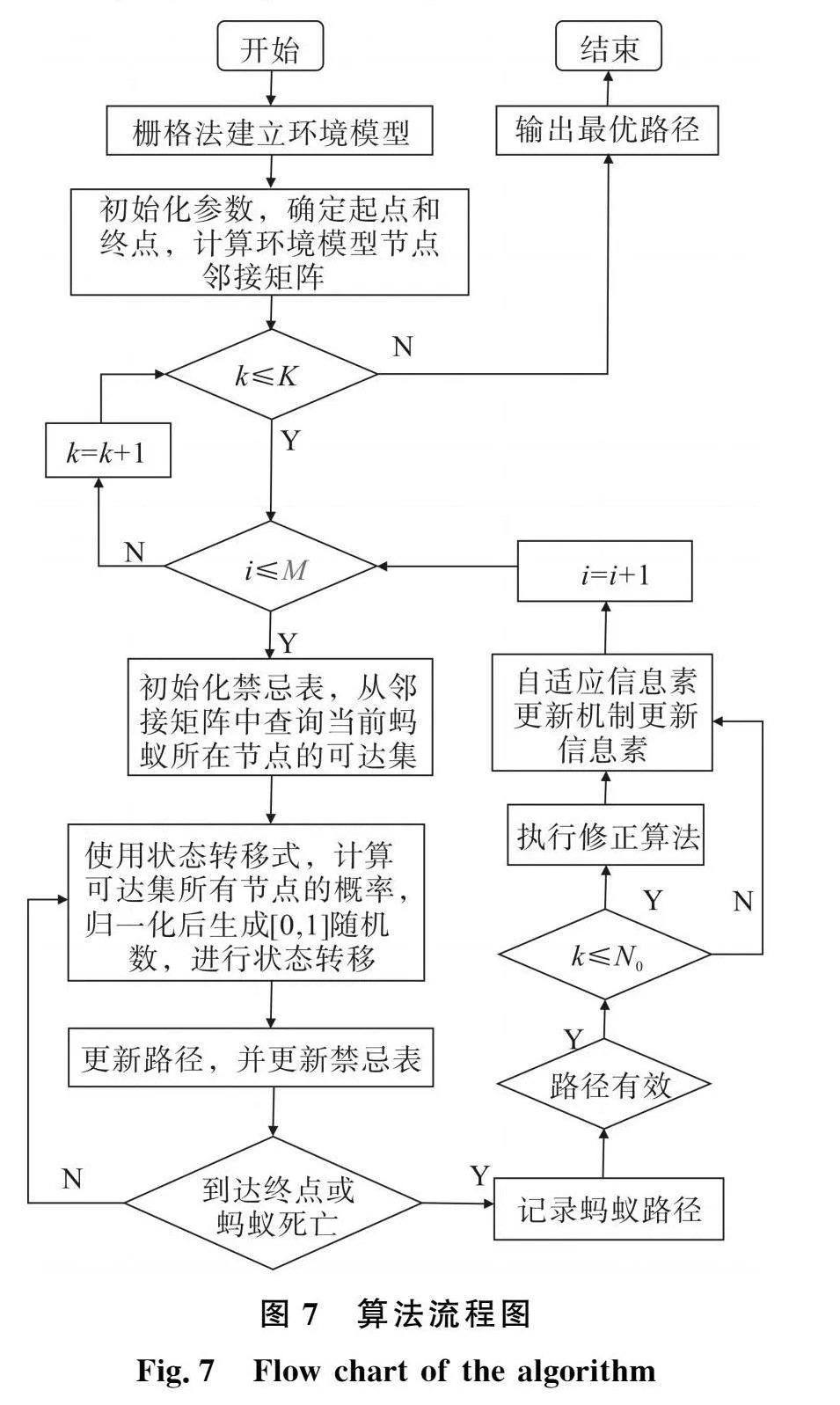
改进蚁群算法的流程如图7所示，其中k为当前迭代次数，i为当前蚂蚁，K为最大迭代次数，M为蚂蚁数量，N0为改进算法限制参数。

3 仿真

为验证算法性能，引入文献［15］、［20］和基本蚁群算法与本文算法对比。算法运行环境为：Windows10 64bit；处理器AMD Ryzen 7 5800H；主频3.2GHz；内存16GB；仿真平台Matlab R2022a。

3.1 实验参数测定

蚁群算法中的主要参数耦合性很强，近年来没有理想的理论分析方法来确定这些参数，主要采用多次调试的方法，实验基本参数如表1所示，其中K为预设的算法最大迭代次数。在算法执行时，初始化执行次数N0=K且算法全过程执行修正策略，获得收敛时的迭代次数t0，之后令N0=t0；时变挥发律ρt的参数ρ0，t0，ε测定方法采用多次调试的方法，其中ε调整挥发律的曲率，ρ0，t0为调整挥发律初值的参数。值得说明的是：当N0>t0时，算法整体运行时间会增加，但更能保障算法收敛速度和质量；当N0<t0时，运行时间减小，但算法质量会有所影响。

3.2 30×30复杂环境分析

图8为30×30复杂环境实验结果，其中图8a为4种算法最短路径图，图8b为4种算法60次最短距离迭代曲线，可知基本蚁群算法在60次迭代过程中最小路径长度波动下降，波动幅度较大且难以收敛。

文献［15］使蚂蚁从8搜索方向扩大到16搜索方向，具有更强的局部搜索能力，增强了蚂蚁跳出局部最优的能力，但16搜索方向对于更复杂环境仍有局限性，如图8a中多行的坐标（27.5，1.5）为曲折路线，所以迭代曲线具有波动性，且难以收敛。文献［20］利用蚂蚁间通信的方式，使得蚂蚁能够利用历史路径跳出局部陷阱，但蚂蚁的历史路径是有限的，当历史路径中没有跳出局部陷阱的路径时，那么蚂蚁间通信的方式则不能解决局部陷阱问题，例如图8a文献［20］的路径中（3.5，23.5）至（3.5，20.5）。因此，文献［20］虽然有效降低了迭代曲线的波动性，但是对于复杂环境仍难以收敛。

本文提出的修正策略和自适应挥发强度的信息素更新机制，使算法具有修正曲折路径的能力，减少了曲折路径所产生的信息素干扰，从而使算法在复杂环境中迭代曲线波动小、收敛快。

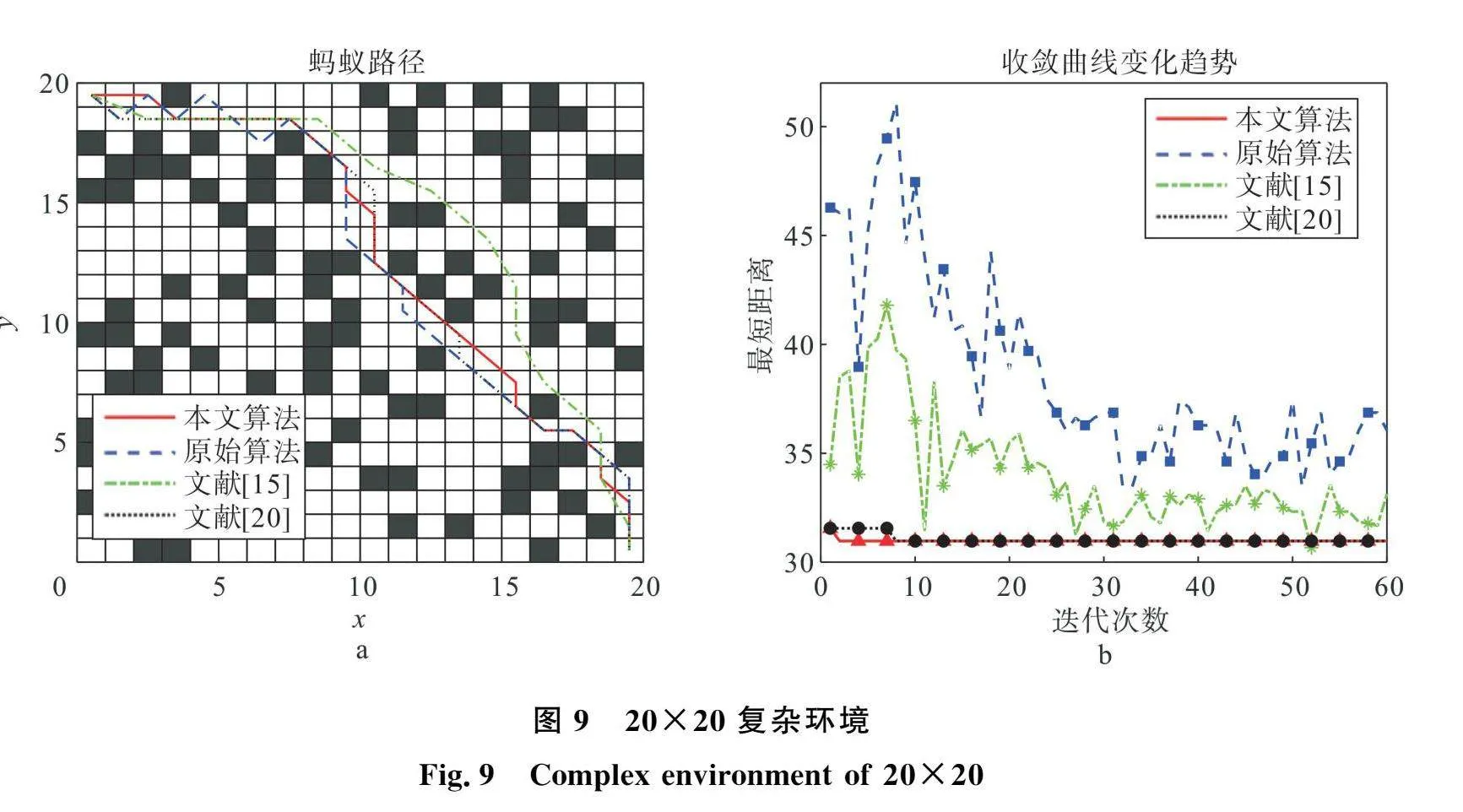
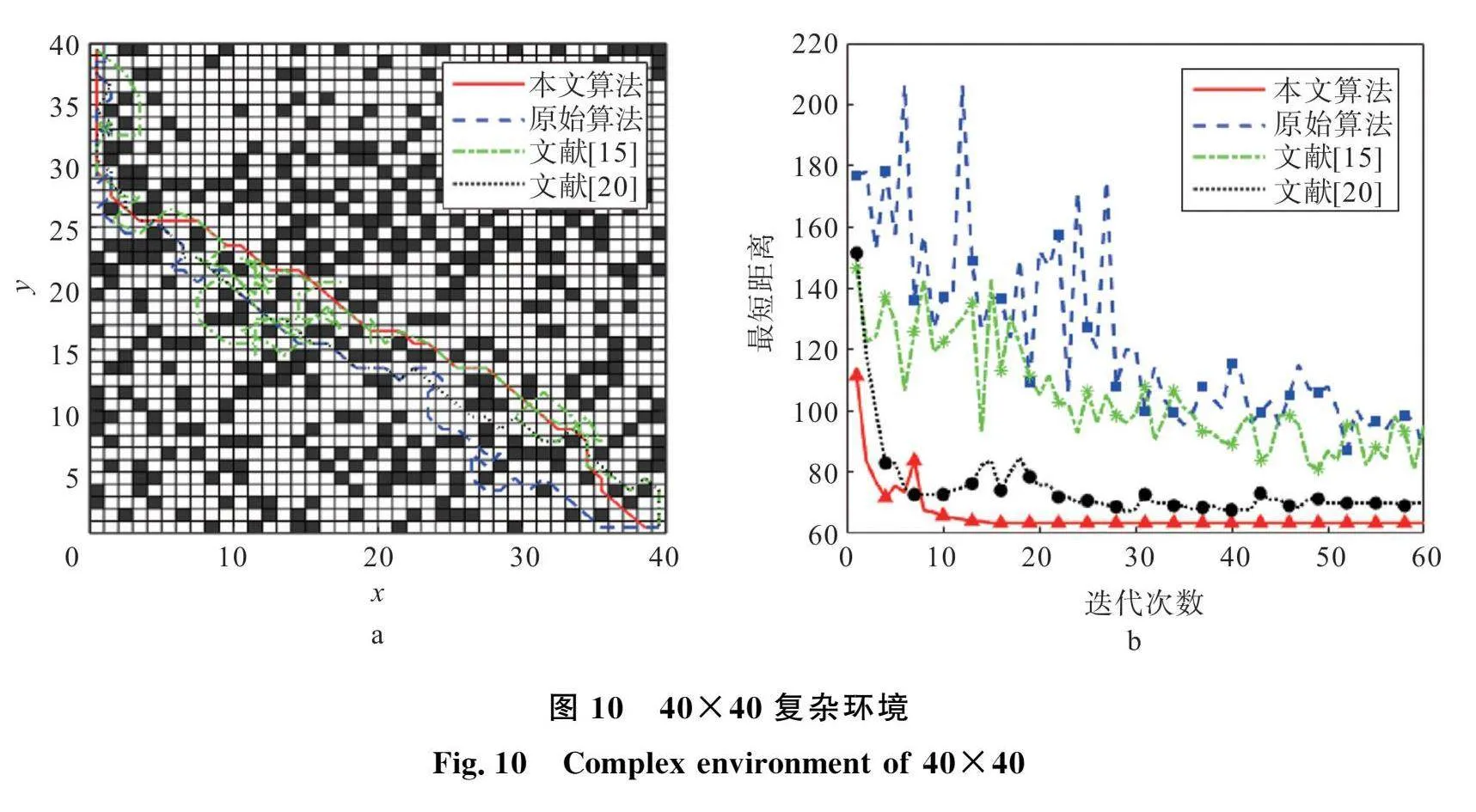
3.3 算法鲁棒性测试

图9a和图10a为20×20和40×40复杂环境，结合图8a的实验环境，进行4种算法的实验。由图8a、图9a和图10a可知，基本蚁群算法在3种情况下曲折路径较多，算法难以收敛。图10b表明：随着环境模型复杂度的增大，文献［15］相比于基本蚁群算法的优越性则变差，迭代曲线已经没有明显优势，其主要原因是16方向的蚂蚁搜索范围有限，使得16搜索方向与8搜索方向性能差距缩小，以致收敛曲线变化趋势几乎一致。

图9b说明，文献［20］在20×20复杂环境能够收敛，但是本文算法收敛速度比之更快，且收敛结果一致。随着环境模型复杂度升高，如图8b中30×30复杂环境，文献［20］中蚂蚁的历史路径对环境模型的覆盖度不足，导致蚂蚁通信性降低，因此会出现一定的波动。本文算法在迭代次数为10时仍能收敛，且收敛质量强于文献［20］。对于图10a中更加复杂的40×40环境，文献［20］的性能则进一步变差，图10b中迭代曲线波动性更大，更加难以收敛，而本文算法则在15次达到收敛，收敛值小于文献［20］最小值。

综上，在4种算法中，从收敛速度考虑基本蚁群算法与文献［15］都不能收敛，文献［20］能在20×20环境下收敛，而更加复杂的环境则不能收敛，算法鲁棒性较差。本文算法在3种测试环境下都能够收敛且鲁棒性较好。从收敛值角度考虑，本文算法<文献［20］<文献［15］<基本蚁群算法。因此，对于收敛速度和收敛值，本文算法>文献［20］>文献［15］>基本蚁群算法。

3.4 统计数据分析

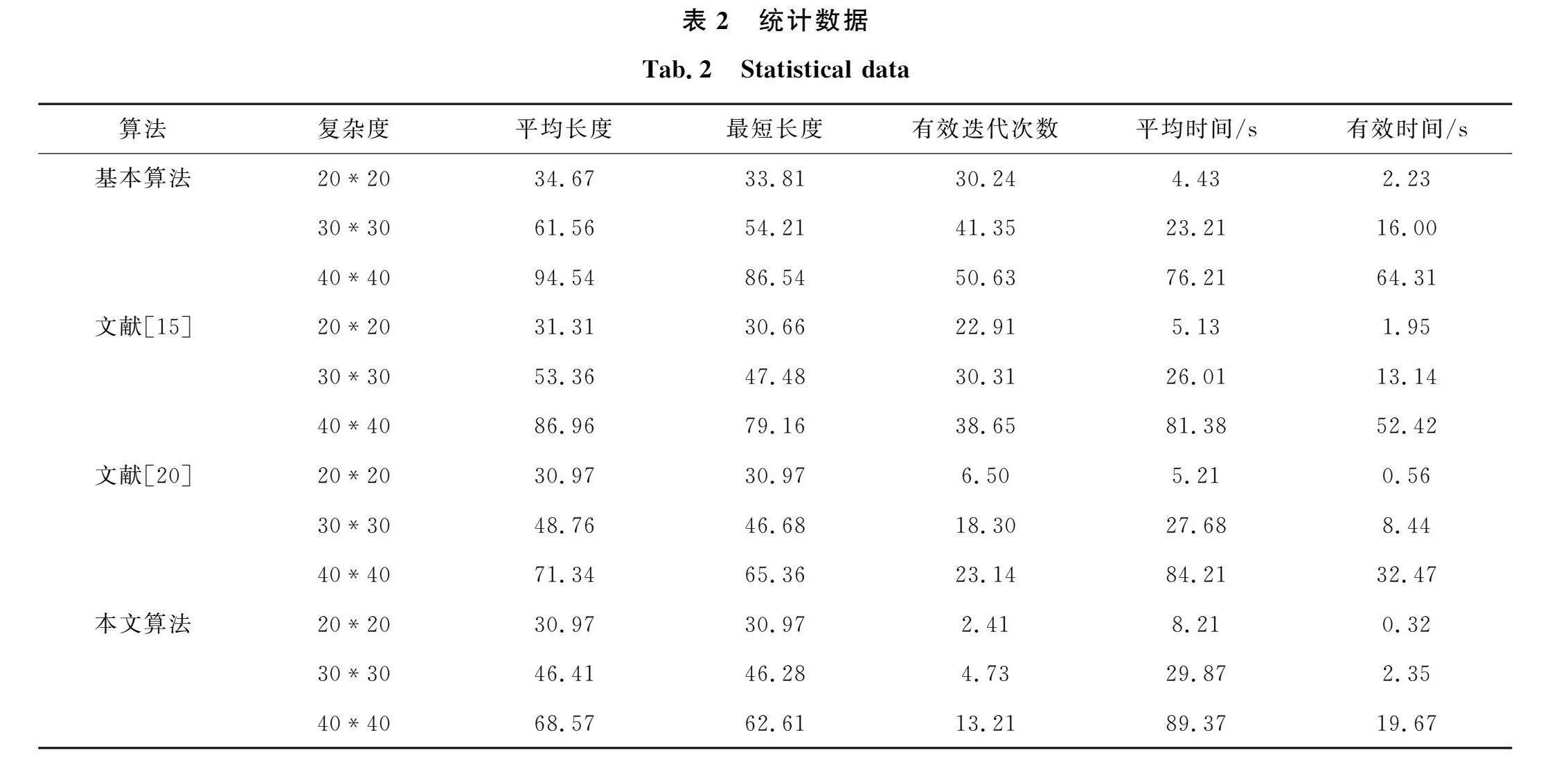
表2为4种算法30次重复实验所得统计数据。可以看出，随着复杂度的升高，4种算法的平均运行时间都有所提升，具体顺序为本文算法>文献［20］>文献［15］>原算法，但是只关注整体平均运行时间并不能有效说明算法的性能。将算法第一次搜索到最短长度时的迭代次数记为有效迭代次数，所花费的时间记为有效时间，从有效时间的角度更能说明算法的时间效率。从表2中可以看出，算法在3种环境模型下的有效时间为本文算法<文献［20］<文献［15］<原算法。因此，从有效时间角度考虑算法性能，本文算法最佳。

此外，在平均长度和最短长度方面，本文算法在3种不同的环境模型下都具有较好的鲁棒性。值得一提的是：文献［15］对于20×20模型，因其蚂蚁搜索方向为16方向，因此在一些特殊情况下的路线可以比8搜索方向的路径更短，但是对于更加复杂的模型，文献［15］则效果不佳。

4 结论

改进的蚁群算法在复杂环境路径规划问题中，难以收敛且收敛结果差。本文针对该问题引入修正策略和自适应信息素更新机制，解决复杂环境模型中收敛难、收敛结果差的问题;然后，介绍了参数的测定方法。最后，通过与文献［15］、［20］以及基本蚁群算法在不同环境模型的对比实验，证明了改进蚁群算法具有较好的适应性和鲁棒性，以及较快的收敛速度和较好的收敛结果。此外，本文引入的修正策略具有时间复杂度较高的不足，如何寻找时间复杂度更低的路径优化策略是下一步值得考虑的问题。

参考文献：

［1］DORIGO M， MANIEZZO V， COLORNI A. Positive feedback as a search strategy［J］. Technical Report， 199 1（1）：91016.

［2］WANG Y H， GAO D M， WANG X D. Shortest path planning based on improved ant colony algorithm［J］. ASP Transactions on Computes， 202 1（3）：611.

［3］AKKA K， KHABER F. Mobile robot path planning using an improved ant colony optimization［J］. International Journal of Advanced Robotic Systems， 2018， 15（3）：17.

［4］BULLNHEIMER B， HARTL R F， STRAUSS C. An improved ant system algorithm for the vehicle routing problem［J］， Annals+BOL2NiImws8kmiTPx1vvQ== of Operations Research， 1999， 89：319328.

［5］CARO D. Antnet： distributed stigmergetic control for communications networks［J］. Journal of Artificial Intelligent Research， 1999， 9（1）： 317365.

［6］HOU W B， XIONG Z H， WANG C S， et al. Enhanced ant colony algorithm with communication mechanism for mobile robot path planning［J］. Robotics and Autonomous Systems， 2022，148： 103949.

［7］LU L C， YUE T W. Mission-oriented ant-team ACO for min-max MTSP［J］. Applied Soft Computing， 2018， 76：436444.

［8］MIAO C W， CHEN G Z， YAN C L， et al. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm［J］. Computers & Industrial Engineering， 202 156：107230.

［9］XUE T， LIU L， LIU S， et al. Path planning of mobile robot based on improved ant colony algorithm for logistics［J］. Mathematical Biosciences and Engineering， 202 18（4）： 30343045.

［10］ 孔珊，仲昭林，张纪会.多路径选择变速双目标物流配送路径规划［J］.复杂系统与复杂性科学， 2022， 19（1）：7480.

KONG S， ZHONG Z L， ZHANG J H. Bi-objective vehicle routing problems with path choice and variable speed［J］. Complex System and Complexity Science， 2022， 19（1）：7480.

［11］ 江明，王飞，葛愿，等.基于改进蚁群算法的移动机器人路径规划研究［J］.仪器仪表学报， 2019， 40（2）： 113121.

JIANG M， WANG F， GE Y， et al. Research on path planning of mobile robot based on improved ant colony algorithm［J］. Chinese Journal of Scientific Instrument， 2019， 40（2）： 113121.

［12］ 王晓燕，杨乐，张宇，等. 基于改进势场蚁群算法的机器人路径规划［J］.控制与决策， 2018， 33（10）： 17751781.

WANG X Y， YANG L， ZHANG Y， et al， et al. Robot path planning based on improved ant colony algorithm with potential field heuristic［J］. Control and Decision， 2018， 33（10）： 17751781.

［13］ 徐兴，钱誉钦，赵芸，等.基于改进蚁群算法的立体仓库三维空间路径优化［J］.计算机集成制造系统， 202 27（1）： 207214.

XU X， QIAN Y Q， ZHAO Y， et al.3D spatial path optimization of stereo warehouse based on improved ant colony algorithm［J］.Computer Integrated Manufacturing Systems， 202 27（1）： 207214.

［14］ 徐小斐，陈婧，饶运清，等.迁移蚁群强化学习算法及其在矩形排样中的应用［J］.计算机集成制造系统， 2020， 26（12）： 32363247.

XU X F， CHEN J， RAO Y Q， et al. Transfer ants reinforcement learning algorithm and its application on rectangular packing problem［J］. Computer Integratedf67f247836e8b897415174e7eead9e88 Manufacturing Systems， 202 36（7）： 15811591.

［15］ 徐菱，付文浩，江文辉，等.基于16方向24邻域改进蚁群算法的移动机器人路径规划［J］.控制与决策， 202 36（5）： 11371146.

XU L， FU W H， JIANG W H， et al. Mobile robots path planning based on 16-directions 24-neighborhoods improved ant colony algorithm［J］. Control and Decision， 202 36（5）： 11371146.

［16］ DEBORA D C， ALI E， HAMIDREZA A， et al. A novel ant colony algorithm for solving shortest path problems with fuzzy arc weights［J］. Alexandria Engineering Journal， 2022， 61： 34033415.

［17］ 张恒，何丽，袁亮，等.基于改进双层蚁群算法的移动机器人路径规划［J］.控制与决策， 2022， 37（2）： 303313.

ZHANG H， HE L， YUAN L， et al. Mobile robot path planning using improved double-layer ant colony algorithm［J］. Control and Decision， 2022， 37（2）： 303313.

［18］ 张玮，马焱，赵捍东，等.基于改进烟花蚁群混合算法的智能移动体避障路径规划［J］.控制与决策， 2019， 34（2）： 335343.

ZHANG W， MA Y， ZHAO H D， et al. Obstacle avoidance path planning of intelligent mobile based on improved fireworks-ant colony hybrid algorithm［J］. Control and Decision， 2019， 34（2）： 335343.

［19］ 邓丽娟，张纪会.混合蚁群算法求解双目标时间窗VRP［J］.复杂系统与复杂性科学，2020，17（4）：7384.

DENG L J， ZHANG J H. A hybrid ant colony optimization for bi-objective VRP with time windows［J］. Complex System and Complexity Science， 2020， 17（4）： 7384.

［20］ HOU W B， XIONG Z H， WANG C S， et al. Enhanced ant colony algorithm with communication mechanism for mobile robot path planning［J］. Robotics and Autonomous Systems， 2022， 148：103949.

（责任编辑 李 进）