一类多涡卷Chua系统及其在图像加密中的应用

摘要： 为使混沌序列表现出更复杂的特性，在典型的Chua系统上引入了分段线性函数，使所得的系统产生可控数量的多涡卷吸引子。对该系统进行动力学分析，分析结果表明，该系统混沌特性分布广泛，具有丰富的动力学行为。在此基础上，提出了一种基于Zigzag置乱和DNA编码的加密算法，并从多个方面对该算法的安全性进行了分析。仿真结果验证了该方法不仅能对图像进行有效加密，而且能有效抵抗各种常见的攻击，为图像加密提供了理论依据。

关键词： 多涡卷Chua系统；混沌序列；图像加密；Zigzag置乱；DNA编码

中图分类号： TP391.9；O415.5文献标识码： A

A Multi-scroll Chua System and Its Application in Image Encryption

LIU Siyang， AN Xinlei， SHI Qianqian， WANG Yue

（School of Mathematics and Physics， Lanzhou Jiaotong University， Lanzhou 730070， China）

Abstract：In order to make the chaotic sequence show more complex characteristics， a piecewise linear function is introduced into the typical Chua’s system to produce a controllable number of multi-scroll attractors. The dynamic analysis of this system is performed， and the results illustrate that the chaotic characteristics of the system are widely distributed and have rich dynamic behaviors. On this basis， an encryption algorithm based on Zigzag scrambling and DNA coding is proposed， and its security is analyzed from multiple aspects. ThNgLQlFr6aWgp8bQk16P3g==he simulation results indicate that this method can not only encrypt the image effectively， but also resist a variety of common attacks effectively， which provides a theoretical basis for image encryption.

Keywords： multi-scroll Chua system; chaotic sequence; image encryption; Zigzag scrambling; DNA coding

0 引言

近年来，随着5G技术以及物联网的发展，网络系统和分布式多媒体系统在通信技术中得到了大量发展，图像在日常通讯、商业、军事、教育及医疗等方面得到更加广泛的应用［1］。在信息发送和接收设备发展较为完备的同时，也为非法访问并获得通信数据提供了便利，因此图像信息安全已成为一项重要而紧迫的问题。

随着混沌理论逐渐成熟，越来越多的学者将混沌系统用于图像加密的研究工作中。基于混沌系统的数字图像加密算法的安全程度取决于混沌序列的复杂度，混沌系统复杂范围越广，应用于加密算法的安全性越高［2］。因此，设计一个新的较为复杂的混沌系统在通信保密方面具有重大意义。近年来，一些学者在混沌系统的设计上提供了新的思路［35］。禹等［3］以变型蔡氏电路和四阶蔡氏电路为例，提出一种研究四维系统中多涡卷混沌与超混沌吸引子的方法，为多涡卷混沌系统设计提供了新的思路。贾等［4］采用对数函数序列构造了一个新Chua多涡卷混沌系统，并设计一个递归反步控制器控制Chua多涡卷混沌系统中的混沌行为。Sahoo等［5］以Chen系统和Lu系统为例，将原系统的一个非线性项乘以一个非线性函数，得到多翼吸引子，通过改变新添加的非线性函数的参数来改变平衡点的数量，通过改变平衡点的数量来改变翅膀的数量。在图像加密应用方向，文献［6，7］在神经元模型中引入磁通变量，提出一类基于电磁感应的神经元模型，应用于图像加密具有较好的加密效果。摆等［8］提出一种三涡卷混沌系统并进行了电路模拟，结合DNA算法设计了一种彩色图像加密算法。文献［913］通过分段耦合两个或者多个低维混沌系统生成一个新的混沌系统，再结合图像置乱扩散算法，取得较好的加密效果。除了整数阶混沌系统外，近年来，许多学者提出基于分数阶混沌系统的加密算法，例如文献［1417］均设计了一类基于分数阶混沌系统的图像加密算法，该类算法加密效果好，但运算时间相对较长。Wu等［18］提出了一种基于CML的NCA时空混沌，结合DNA序列操作、一次性密钥设计了一种彩色图像加密算法。方等［19］提出一个新四维超混沌，生成的伪随机序列作为密钥流，并利用密钥流对彩色图像像素块进行置乱及像素扩散运算。

本文提出了一类基于多涡卷蔡氏电路混沌系统的图像加密方法。在经典的Chua系统基础上引入分段线性函数，形成一个新的多涡卷Chua混沌系统。相比经典的Chua系统，该系统产生的混沌序列更为复杂；相比广义的四维变式Chua系统，该系统运算速度更快。利用多涡卷Chua混沌系统产生混沌序列，结合Zigzag置乱和DNA编码设计了一个新的数字图像加密算法。相关的安全性分析和仿真试验表明，该加密算法安全性高，速度快且易于实现。

1 系统描述

1986年，Chua等［20］提出经典的Chua系统，在此系统上引入多分段线性函数f（x），用该函数产生多涡卷Chua系统描述如下：

=ay-f（x）=x-y+z=-by（1）

其中，多分段线性函数f（x）的表达式为［3］

f（x）=mNx+0.5∑Ni=1（mi-1-mi）（|x+Ei|-|x-Ei|），N=，3，…

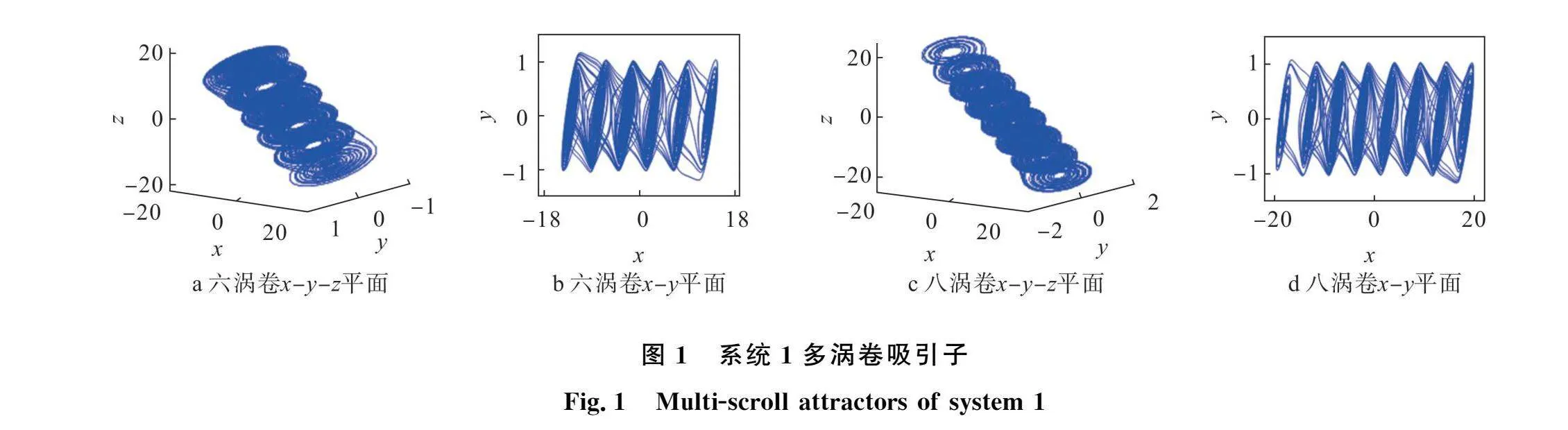
f（x）为奇函数，可用于产生偶数个涡卷，N用于控制系统产生涡卷的个数，当N=n，n=，3，…时，可产生n+1个涡卷吸引子，En用递归公式（1+2∑n-1i=1m0mi）E1表示。例如，取m0=m2=m4=-0.5，m1=m3=m5=0.5，E1=1.3，当N=5时，可得到六涡卷吸引子；当N=7时，可得到八涡卷吸引子。

在系统（1）中，分别令a=10，b=15，m0=m2=m4=-0.5，m1=m3=m5=0.5，E1=1.3；初始值为x0=1，y0=1，z0=1；分别取N=5，N=7，产生的多涡卷吸引子如图1所示。

2 动力学分析

2.1 平衡点稳定性分析

以N=5为例研究多涡卷Chua系统的动力学特性。对于系统（1），固定参数a=10，b=15，m0=m2=m4=-0.5，m1=m3=m5=0.5，E1=1.3，初值为x0=1，y0=1，z0=1，令

ay-f（x）=0x-y+z=0-by=0

数值计算求得系统（1）有6个平衡点S1=（0，0，0），S2=（2.6，0，-2.6），S3=（5.2，0，-5.2），S4=（7.8，0，-7.8），S5=（10.4，0，-10.4），S6=（13，0，-13）。其中平衡点S1，S3，S5有相同的特征值λ1=6.049 4，λ2，3=-1.024 7±3.368 7i，这表明S1，S3，S5均为指标1的鞍焦点，用于形成连接涡卷之间的键带；平衡点S2，S4，S6有相同的特征值λ1=-6.301 7，λ2，3=0.150 9±3.446 6i，这表明S2，S4，S6均为指标2的鞍焦点，用于产生涡卷［34］。

2.2 分岔图和Lyapunov指数谱分析

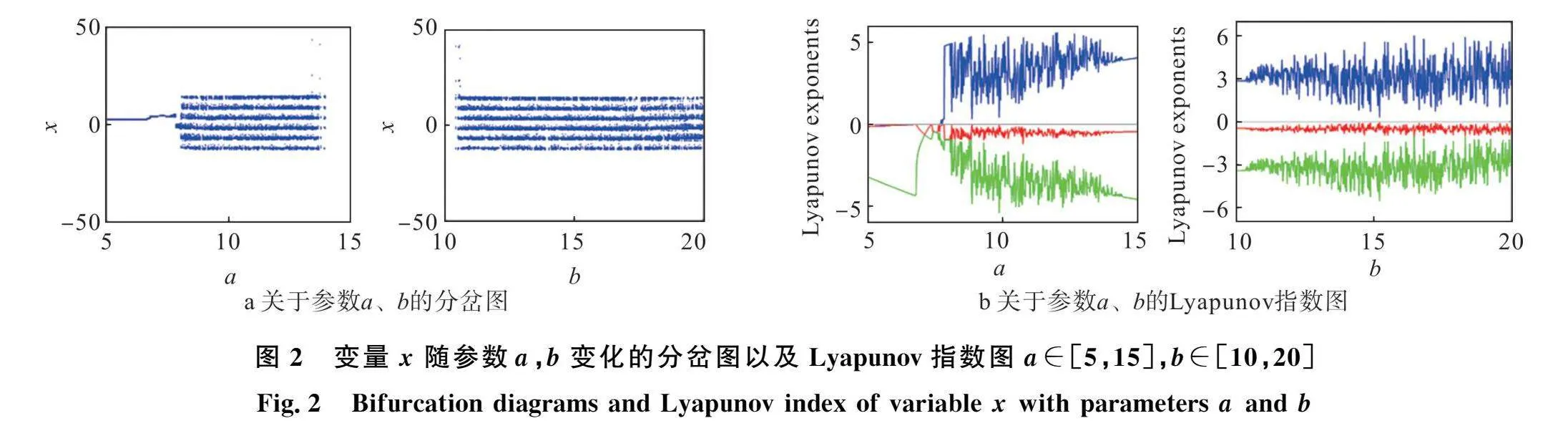
分岔图可以直观地体现出系统运动状态随参数改变而发生的变化。Lyapunov指数描述了在一段时间内相空间相邻轨迹的平均指数发散率，可以看到系统的运动特征。保持系统参数和初始值不变，得到参数a，b关于状态变量x的分岔图以及Lyapunov指数谱如图2所示。

3 基于Zigzag置乱和DNA运算的图像加密算法

3.1 Zigzag置乱

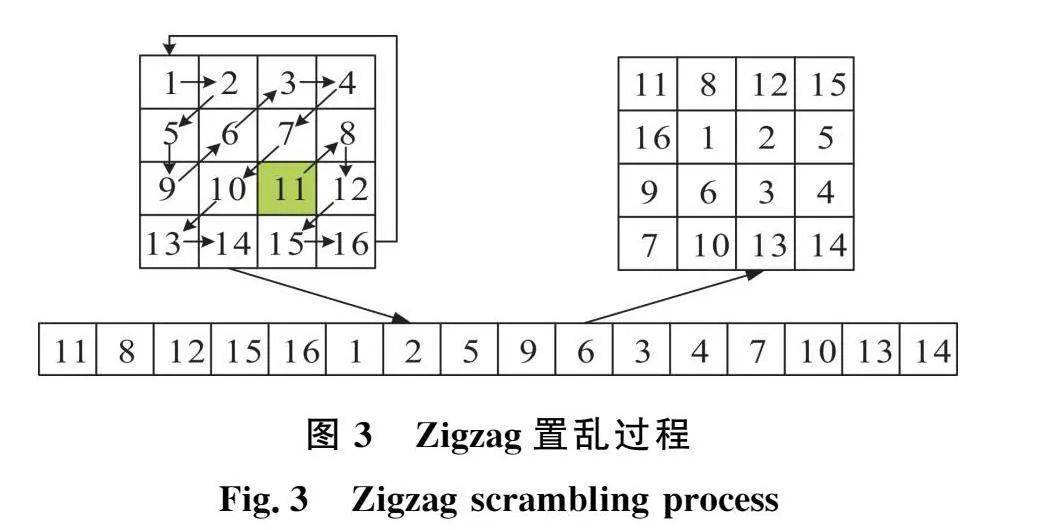
Zigzag置乱算法能够有效、快速地改变图像像素位置，因此广泛应用于图像加密领域。该算法从矩阵左上角取一个数字，按Z字型路径依次扫描矩阵中的数字，将扫描到的数字排成一维数组并重新组合成与原矩阵大小相同的矩阵。本文对上述算法进行改进，把矩阵分为4×4的子块，从（3，3）位置处开始扫描，如图3所示。

3.2 DNA编码操作

DNA编码是一种生物学上的技术，具有种类特殊性，处理信息时遵循其自身的互补规律，因此融入DNA编码的加密算法更有保密优势。一个DNA序列由4个核酸碱基组成，分别是胞嘧啶（C）、腺嘌呤（A）、鸟嘌呤（G）、胸腺嘧啶（T），其中碱基A和T互补，C和G互补。在二进制系统中，“00”和“11”配对，“01”和“10”配对的规则和DNA碱基配对规则有些类似。对于单通道灰度图像而言，通常每个像素由8比特的二进制数字表示，把8比特的二进制数字两两拆分成四组，可得到四组二进制数字，这就可以和DNA的四种碱基对应起来，于是可以用DNA编码来存储图片中的每个像素值。基于DNA编码的图像加密算法需要充分利用有限的DNA编码种类和DNA操作类型。按照排列组合，DNA四种碱基与四组二进制数字有24种匹配方法，但其中只有8种匹配方法符合Watson-Crick互补规则［21］，如表1中所列。此外，DNA编码同样具有加减法、异或等运算规则，在表2中列出。

DNA编码有其自己的配对规则，即A，T互相配对，C，G互相配对。于是，若碱基xi为碱基L（xi）为的互补对，则xi应满足公式（2）：

xi≠L（xi）≠L（L（xi））≠L（L（L（xi）））xi=L（L（L（L（xi））））（2）

由式（2）可知，一共有6种组合满足DNA碱基互补规则，分别在式（3）中表述。在设计加密算法时，可随机选择这6种组合中的一种对碱基进行互补置换，这样可达到像素扩散的目的。

L1（A）=T，L1（T）=C，L1（C）=G，L1（G）=AL2（A）=T，L2（T）=G，L2（G）=C，L2（C）=AL3（A）=C，L3（C）=T，L3（T）=G，L3（G）=AL4（A）=C，L4（C）=G，L4（G）=T，L4（T）=AL5（A）=G，L5（G）=T，L5（T）=C，L5（C）=AL6（A）=G，L6（G）=C，L6（C）=T，L6（T）=A（3）

3.3 加密算法

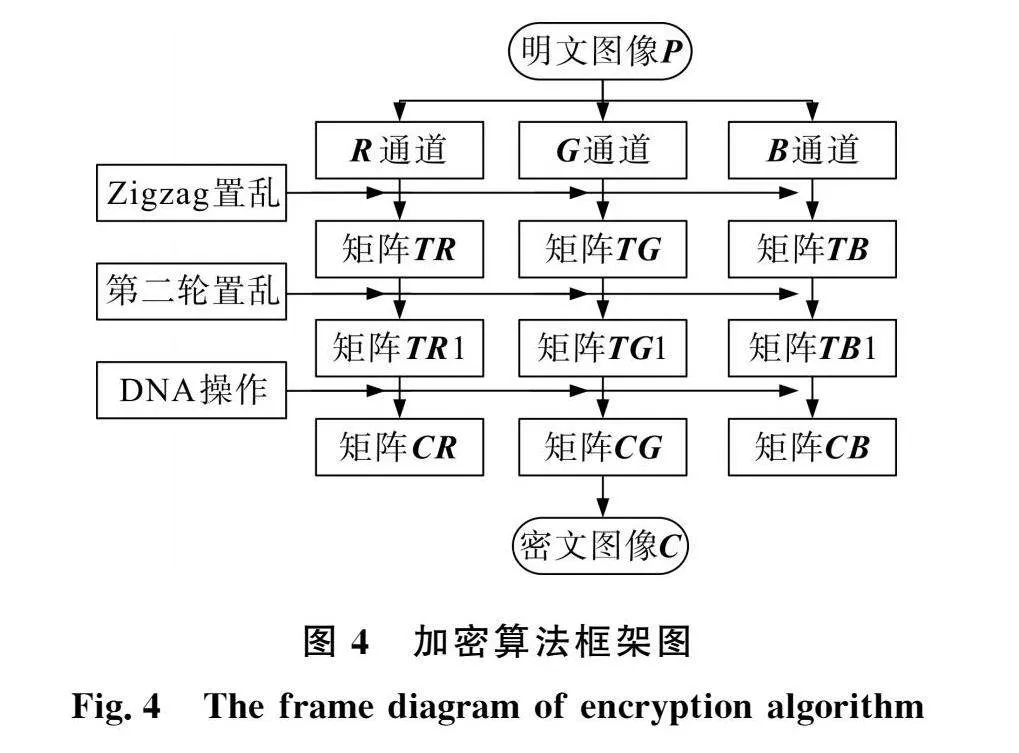
第1步：输入明文图像P（M×N×3），将其分解成红、绿、蓝三色通道，得到分量矩阵PR（M×N），PG（M×N）和PB（M×N）。

第2步：选取参数和初值，使系统（1）处于混沌状态。先让系统（1）迭代800次消除暂态效应，然后再迭代MN次得到长度为MN的混沌序列xi，yi和zi，i=，…，MN，将混沌序列按式（4）进行量化处理并排列成矩阵X（M×N），Y（M×N）和Z（M×N）：

x（i）=mod（floor（abs（x（i））×1016），256）y（i）=mod（floor（abs（y（i））×1016），256）z（i）=mod（floor（abs（z（i））×1016），256）（4）

第3步：对分量矩阵PR，PG和PB分别采用改进的Zigzag置乱生成M×N的数字矩阵TR，TG和TB。

第4步：将生成的数字矩阵TR和矩阵X，TG和矩阵Y，TB和矩阵Z分别按式（5）进行第二次置乱得到矩阵TR1，TG1和TB1：

TR1（I（i，j-1），j-i）=TR（I（i，j），j），j>iTR1（I（i，N+j-i），N+j-i）=TR（I（i，j），j），j≤i

TG1（I（i，j-1），j-i）=TG（I（i，j），j），j>iTG1（I（i，N+j-i），N+j-i）=TG（I（i，j），j），j≤i

TB1（I（i，j-1），j-i）=TB（I（i，j），j），j>iTB1（I（i，N+j-i），N+j-i）=TB（I（i，j），j），j≤i（5）

第5步：将数字矩阵TR1，TG1和TB1转化为M×8N的二进制矩阵，再将得到的二进制矩阵按照第r1种DNA编码规则转化为M×4N的DNA矩阵S1，S2和S3。

第6步：将第二步中得到的混沌序列xi，yi和zi分别转化成长度为M×8N的二进制序列，再将得到的二进制序列按照第r2种DNA编码规则分别转化成长度为M×4N的DNA序列，并将得到的DNA序列分别整形为M×4N的矩阵K1，K2和K3用于进行DNA加法操作。

第7步：根据DNA互补规则，将DNA矩阵S1，S2和S3展开成长度为1×4MN的一维DNA序列分别按以下方法进行互补转化得到DNA序列S1_R，S2_G和S3_B：

若c2i-2=A，则c2i-1=Ll1（d2i-1）；若c2i-2=C，则c2i-1=Ll2（d2i-1）；

若c2i-2=G，则c2i-1=Ll3（d2i-1）；若c2i-2=T，则c2i-1=Ll4（d2i-1）；

若c2i-1=A，则c2i=Ll5（d2i）；若c2i-1=C，则c2i=Ll6（d2i）；

若c2i-1=G，则c2i=Ll7（d2i）；若c2i-1=T，则c2i=Ll8（d2i）。

其中，ci，i=，…，4MN表示互补前展开的一维DNA序列中的元素，di，i=，…，4MN表示互补后所生成的一维DNA序列中的元素，li，i=，…，8表示任意一种互补原则。

第8步：将DNA序列S1_R，S2_G和S3_B排列为M×4N的DNA矩阵DR，DG和DB并与第6步中得到的DNA矩阵K1，K2和K3按照式（6）进行第一轮DNA加法运算得到DNA矩阵DR1，DG1和DB1：

DR1（1）=DR（1）+K1（1）+DR（4MN）DR1（i）=DR（i）+K1（i）+DR1（i-1）

DG1（1）=DG（1）+K2（1）+DG（4MN）DG1（i）=DG（i）+K2（i）+DG1（i-1）

DB1（1）=DB（1）+K3（1）+DB（4MN）DB1（i）=DB（i）+K3（i）+DB1（i-1）（6）

第9步：对DNA矩阵DR1，DG1和DB1再次进行同样的DNA加法运算得到DNA矩阵DR2，DG2和DB2。

第10步：将得到的DNA矩阵DR2，DG2和DB2按照第r3种DNA编码规则解码为二进制矩阵后再转化为M×N的数字矩阵得到矩阵CR，CG和CB。

第11步：最后，将矩阵CR，CG和CB合并为矩阵C得到最终的加密图像。

3.4 实验结果

本文的实验环境为：内存12GB，处理器Intel Core i77500U（2.7GHz/L3 4M），操作系统Windows 10，仿真软件为MATLAB R2018b。选择尺寸均为256×256的彩色图像Lena和Sailboat图像进行实验。保持系统（1）的参数和初始值不变，经过数值仿真得到Lena和Sailboat的加密图像如图5b和图5e所示，相应的解密图像如5c和图5f所示。结果表明，采用所提方法对图像进行加密后能够有效隐藏明文图像的信息，说明所提加密算法的有效性。并且明文图像所隐藏的全部信息在解密后得以完全恢复，这表明了算法具有可行性和有效性。

4 加密算法性能分析

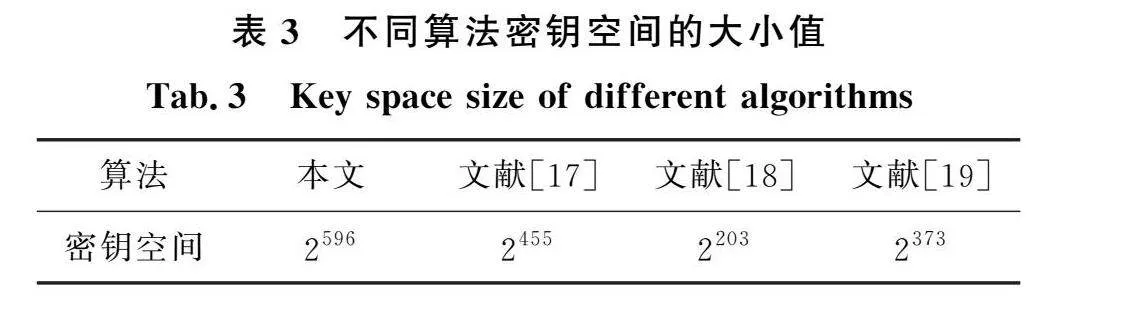
4.1 密钥空间分析

加密算法的密钥空间是衡量一个算法是否可以抵抗穷举攻击的重要特征。本文所使用的图像加密系统的密钥主要包括：系统参数a，b，m0，m1，m2，m3，m4，m5，初始值x0，y0，z0。其中系统参数a，b，m3以及初始值x0，y0，z0的计算精度均为1015，m0，m1，m2，m4，m5的计算精度均为1016；初始碱基c0∈{A，T，G，C}，DNA编码规则r r2，r3∈［ 8］和DNA互补规则li∈［ 6］，i=，…，8。计算得密钥空间大小为4×83×68×1015×6+16×5≈2596，远远大于密码系统的理论密钥空间值2100。另外，在表3中比较了不同算法密钥空间的大小值，可以看出本文所提算法的密钥空间相对较大，可以更有效地抵抗穷举攻击。

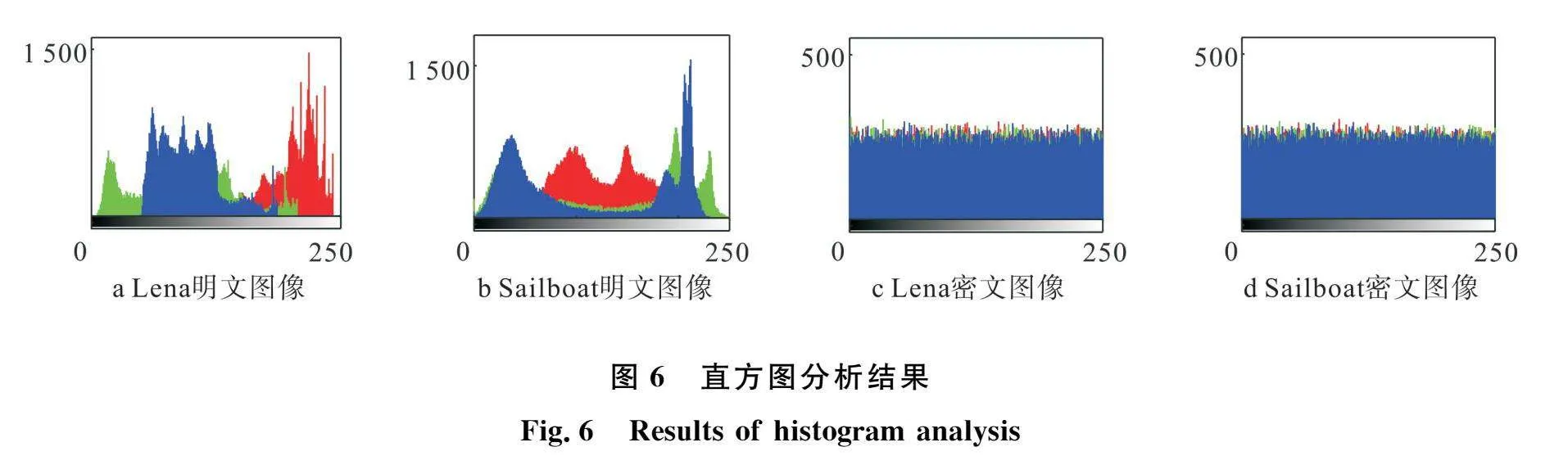
4.2 直方图分析

图像的直方图可以精确、直接地反映出像素值的分布情况，通常用于检测加密后的图像是否有抵抗统计攻击的能力。本节对Lena和Sailboat图像进行测试，数值仿真结果如图6所示。图6a和图6b分别为Lena和Sailboat明文图像直方图，图6c和图6d分别为Lena和Sailboat密文图像直方图，可以明显看出密文图像的像素值分布近似均匀，说明本文所提算法可以有效抵抗统计攻击。

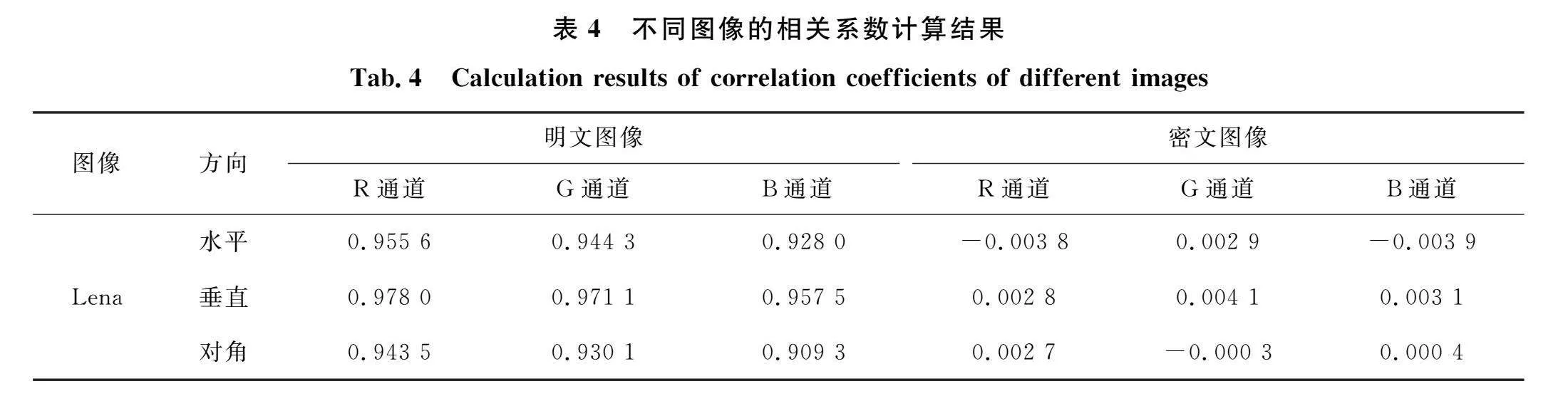
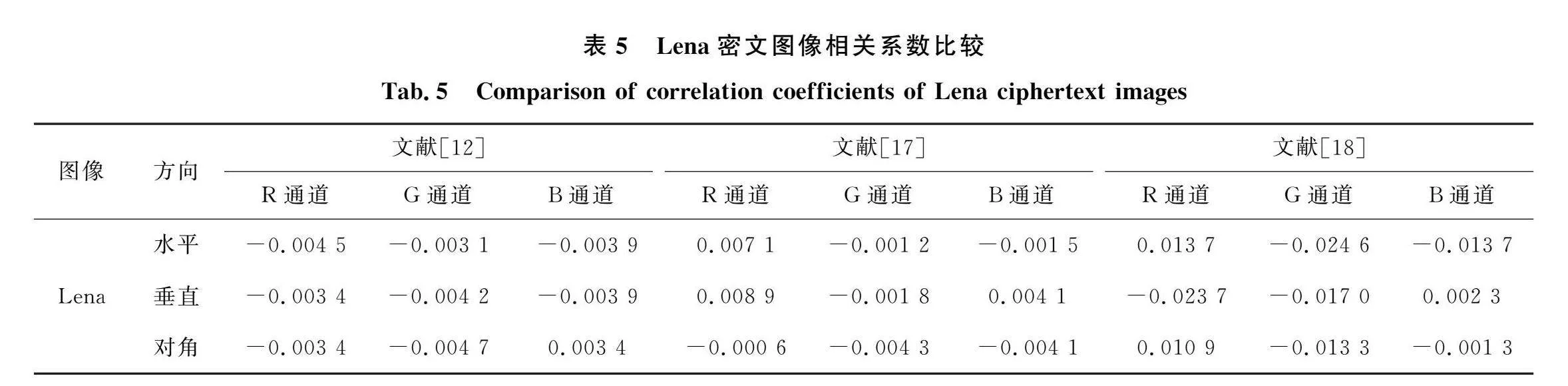
4.3 相邻像素间相关性分析

像素的相关性用来描述图像相邻像素之间相似的程度。对于加密图像来说，像素之间的相关性越低就表明加密算法的安全性越高，加密效果越好。本节选取Lena图像，在R、G、B 3个通道上对水平、垂直、对角3个方向进行测试，在表4中列出了Lena图像明文和密文的相关系数在R、G、B 3个通道上的计算值，可以看出密文图像的3个通道中各个方向上相关性的计算值均显著降低，说明本文算法具有较好的抵抗统计攻击的能力。另外，在表5中列出不同算法中Lena图像的相关性数值，与表4中的计算结果相比可以看出本文所提算法具有一定的优越性。

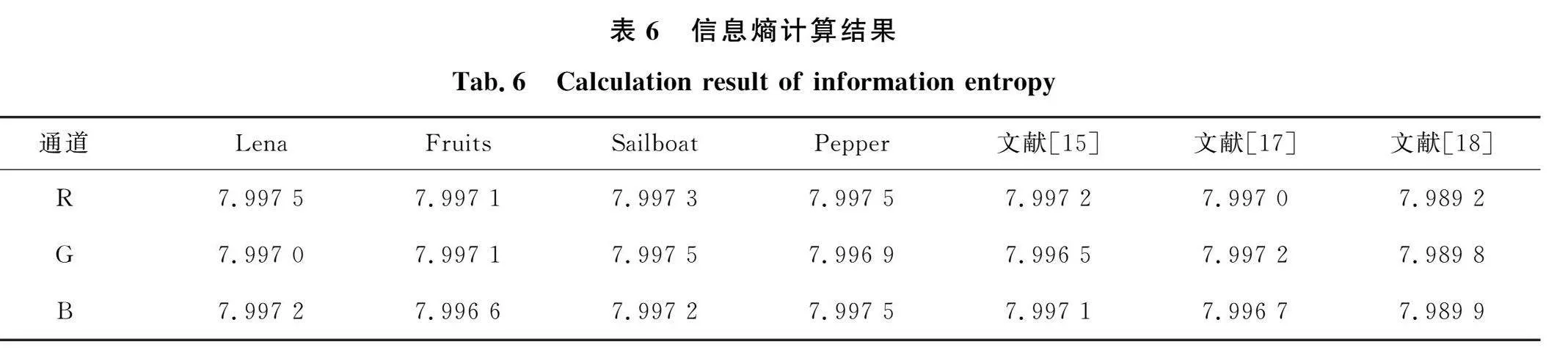
4.4 信息熵分析

信息熵用于描述信息的混乱程度，可以反映图像信息的随机性，是测试加密算法是否安全的重要指标。图像中的信息越混乱，信息熵的值就越大。对于灰度等级为L=256的图像，其信息熵H的理论值为8。在表6中列出了不同密文图像信息熵的数值计算结果，信息熵均接近于理论值。此外，在表6中还比较了不同算法下Lena密文图像信息熵的值，可以看到使用本文所提算法加密后图像的信息熵更接近于8。

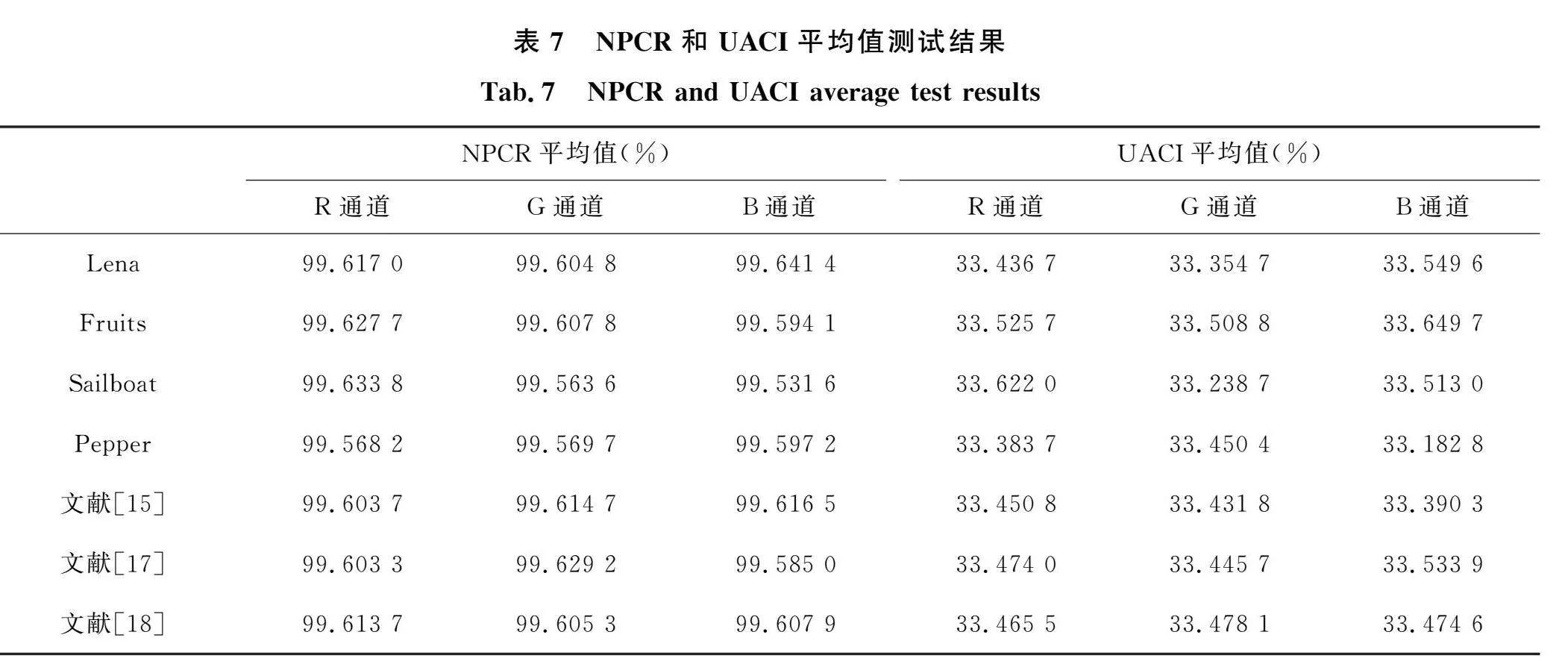
4.5 差分攻击分析

为了抵抗差异攻击，加密系统应该确保在原始图像中有任何微小的修改都会导致加密后的图像出现显著差异。评估算法能否抵抗差分攻击通过平均像素变化率（NPCR）和归一化平均变化强度（UACI）来判断。在理想情况下，NPCR和UACI的值分别为99.609 4%和33.463 5%［14］。本文对不同图像进行实验，得到表7中的结果。另外在表7中还列举了不同算法下Lena图像的测试结果，可见本文算法下的实验对象NPCR以及UACI平均值均非常接近于理想值，这说明本文所提算法可以有效地抵抗差分攻击。

4.6 剪切攻击

在实际传输过程中，数字图像会不可避免地受到噪声干扰、数据丢失等影响，为检测本文所提算法抵抗剪切攻击的能力，本节对Sailboat密文图像进行不同程度的剪切测试。在图7中，对Sailboat密文分别进行了116、18和14的剪切，如图7a、图7b和图7c所示，且恢复后得到的图像分别如图7d、图7e和图7f依次所示。从图中可以看出，当密文图像受到不同程度的信息丢失时，解密后仍可获得明文图像的主要信息，这表明本文所提算法对噪声干扰和数据丢失攻击具有较强的鲁棒性。

5 结论

在经典Chua系统中引入多分段线性函数，使混沌系统产生可控的偶数个涡卷，让多涡卷Chua系统产生的混沌序列复杂性更强。从分岔图、Lyapunov指数谱等方面对该系统进行数值仿真，验证结果表明该系统混沌范围较广，适用于图像加密。基于多涡卷Chua系统设计了一个彩色图像加密算法：先对图像进行Zigzag置乱，为保证加密效果，在Zigzag置乱后再进行一次像素置乱，接着对置乱后的图像进行DNA编码操作得到加密图像。对所设计的加密算法进行安全性测试，测试结果表明该算法的安全性较高，可以有效抵抗各种攻击，为图像加密提供了理论依据。在今后的工作中，将继续研究不同特性的混沌系统并应用于图像加密算法。

参考文献：

［1］王雪荣， 刘浩. 5G框架下数字图像加密技术的发展趋势［J］. 广东通信技术， 2019， 39（8）： 24.

WANG X R， LIU H. Development trend of digital image encryption technology under 5G framework［J］. Guangdong Communication Technology， 2019， 39（8）： 24.

［2］DU F Y， SHEN Q H， DONG W J， et al. An image encryption system based on chaos principle［C］//2022 IEEE 2nd International Conference on Electronic Technology， Communication and Informa1dWmadmA/LSlhsoD+EKp0w==tion （ICETCI）， Changchun， China： IEEE， 2022： 162167.

［3］禹思敏， 林清华， 丘水生. 四维系统中多涡卷混沌与超混沌吸引子的仿真研究［J］. 物理学报， 2003（1）： 2533.

YU S M， LIN Q H， QIU SS. Simulation investigation on multi-scroll chaotic and hyperchaotic attractors for four-dimensional systems［J］. Acta Physica Sinica， 2003（1）： 2533.

［4］贾美美， 蒋浩刚， 李文静. 新Chua多涡卷混沌吸引子的产生及应用［J］. 物理学报， 2019， 68（13）： 6173.

JIA MM， JIANG H G， LI W J. Generation and application of novel Chua multi-scroll chaotic attractors［J］. Acta Physica Sinica， 2019， 68（13）： 6173.

［5］SAHOO S， ROY B K. Design of multi-wing chaotic systems with higher largest Lyapunov exponent［J］. Chaos， Solitons and Fractals， 2022， 157： 111926.

［6］ZHANG S， ZHENG J， WANG X， et al. Multi-scroll hidden attractor in memristive HR neuron model under electromagnetic radiation and its applications［J］. Chaos： an Interdisciplinary Journal of Nonlinear Science， 202 31（1）： 011101.

［7］安新磊， 熊丽， 乔帅. 电磁驱动下一类混合神经元模型的动力学响应与图像加密应用［J］. 电子与信息学报， 2022， 44： 112.

AN X L， XIONG L， QIAO S. Dynamic response of a class of hybrid neuron model by electromagnetic induction and application of image encryption［J］. Journal of Electronics & Information Technology， 2022， 44： 112.

［8］摆玉龙， 杨阳， 唐丽红. 一个新多涡卷混沌系统的设计及在图像加密中的应用［J］. 电子与信息学报， 202 43（02）： 436444.

BAI Y L， YANG Y， TANG L H. Design of a multi-scroll chaotic system and its application to image encryption［J］. Journal of Electronics & Information Technology， 202 43（2）： 436444.

［9］DEMIRTAS M. A new RGB color image encryption scheme based on cross-channel pixel and bit scrambling using chaos［J］. Optik， 2022， 265： 169430.

［10］ 王永， 龚建， 王明月. 基于三维分段Sine映射的彩色图像加密［J］. 北京理工大学学报， 2022， 42（4）： 415423.

WANG Y， GONG J， WANG M Y. Color image encryption based on three-dimensional piecewise sine map［J］. Transactions of Beijing Institute of Technology， 2022， 42（4）： 415423.

［11］ 刘思聪， 李春彪， 李泳新. 基于指数余弦离散混沌映射的图像加密算法研究［J］. 电子与信息学报， 2022， 44（5）： 17541762.

LIU S C， LI C B， LI Y X. A novel image encryption algorithm based on exponent-cosine chaotic mapping［J］. Journal of Electronics & Information Technology， 2022， 44（5）： 17541762.

［12］ 张昊， 王晓庆， 谢红薇， 等. 基于SCC映射的彩色图像分块压缩加密算法［J］. 计算机工程与设计， 2022， 43（7）： 18011809.

ZHANG H， WANG X Q， XIE H W， et al. Block compression-encryption algorithm for color images coupling SCC chaotic map［J］. Computer Engineering and Design， 2022， 43（7）： 18011809.

［13］ HUA 4to9FT7eY9JQIVSUmnxpNQ==Z Y， ZHOU Y C， HUANG H J. Cosine-transform-based chaotic system for image encryption［J］. Information Sciences， 2019， 480： 403419.

［14］ SHI Q Q， AN X L， XIONG L. Dynamic analysis of fractional- order hyperchaotic system and its application in image encryption ［J］. Physica Scripta， 2022， 97（4）： 045201.

［15］ YANG F F， MOU J， LUO C F， et al. An improved color image encryption scheme and cryptanalysis based on a hyperchaotic sequence［J］. Physica Scripta， 2019， 94（8）： 085206.

［16］ ZAREBNIA M， PARVAZ R. Image encryption algorithm by fractional based chaotic system and framelet transform［J］. Chaos， Solitons and Fractals， 202  152： 111402.

［17］ DONG H， BAI E， JIANG X Q， et al. Color image compression-encryption using fractional-order hyperchaotic system and DNA coding［J］. IEEE Access， 2020， 8： 163524163540.

［18］ WU X， WANG K， WANG X， et al. Color image DNA encryption using NCA map-based CML and one-time keys［J］. Signal Processing， 2018， 148： 272287.

［19］ 方鹏飞， 黄陆光， 娄苗苗， 等. 基于四维超混沌系统的彩色图像加密算法［J］. 计算机工程与设计， 2022， 43（2）： 361369.

FANG P F， HUNAG L G， LOU M M. Color image encryption algorithm based on four dimensional hyperchaotic system［J］. Computer Engineering and Design， 2022， 43（2）： 361369.

［20］ CHUA L， KOMURO M， MATSUMOTO T. The double scroll family［J］. IEEE Transactions on Circuits and Systems， 1986， 33（11）： 10721118.

［21］ WATSON J D， CRICK F H C. Molecular structure of nucleic acids： a structure for deoxyribose nucleic acid［J］. Nature， 1953， 171（4356）： 737738.

（责任编辑 李 进）