基于复杂网络的天然气管道网络风险传播研究

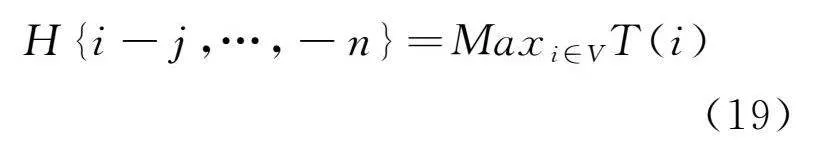
摘要： 为改善管道安全监控与维护，探究天然气管道网络最优风险传播路径。首先，基于复杂网络理论构建网络拓扑结构，利用应用熵权—TOPSIS法对网络节点重要性排序。其次，构建天然气管道网络风险传播模型，定义网络节点失效率和脆弱度，得到蓄意破坏与随机破坏策略下节点的风险传播度和风险最优传播路径。最后，以上海市天然气管道网络为例进行实证分析，结果表明，级联风险情况下的蓄意破坏传播风险度总和大于随机破坏，为管道拓扑优化与维护提供依据。

关键词： 复杂网络；天然气管道网络；风险传播路径；蓄意破坏；随机破坏

中图分类号： X937; N94 文献标识码： A

A Study of Risk Propagation in Natural Gas Pipeline Networks Based on Complex Networks

DAI Jianyong， GAN Meiyan， ZHANG Meirong， MAO Jiazhi， LIU Chao

（a.School of Resource Environment and Safety Engineering; b.Hunan Province Key Laboratory of Emergency Safety

Technology and Equipment for Nuclear Facilities，University of South China， Hengyang 42100 China）

Abstract：To improve pipeline safety monitoring and maintenance， the optimal risk transmission path of the natural gas pipeline network is explored. Firstly， the network topology is constructed based on complex network theory， and the importance of network nodes is ranked by entropy weight-TOPSIS method. Secondly， the risk propagation model of the natural gas pipeline network is constructed， the failure rate and vulnerability of network nodes are defined， and the risk propagation degree and optimal risk propagation path of nodes under deliberate and random failure strategies are obtained. Finally， based on the empirical analysis of the Shanghai natural gas pipeline network， the results show that the total risk of intentional damage propagation is greater than that of random damage in the case of cascade risk， which provides a basis for pipeline topology optimization and maintenance.

Keywords： complex networks；natural gas pipeline network; risk communication routes; deliberate vandalism；random vandalism

0 引言

天然气是一种清洁能源，对用户的供应都逐年增加。天然气处理厂将从油井输送过来的天然气经过脱水工艺流程处理，再通过管网、输气设备输送到用户，这一系列流程在城市中组成了一个管道供气网络。近年来，天然气事故逐年增加，造成了大量财产损失与人员伤亡[1]。发生事故的主要原因是管道设备失效、被人工开挖破坏以及车辆暴力撞坏导致爆炸[2]。如湖北省十堰市“6·13”重大燃气爆炸事故主要是由于第三方施工破坏、自然灾害、管道制造安装质量缺陷问题所导致[3]，且事故的发生造成周围用户供气不稳定的风险。因此，如何找到天然气管道网络供气风险传播路径，为管道安全监控与维护提供重要依据是当前亟需解决的问题。

网络风险传播主要是指网络中的威胁源向周边邻接节点投射风险，其传播途径主要是对节点间以及邻居节点的相互传播[4]。风险传播路径分析是识别天然气供气网络容易受到事故影响的关键路径的问题。由于供气网络复杂性，传统的天然气管道风险因素及设施失效分析方法已不能满足供气系统的安全稳定问题，而利用复杂网络理论研究网络拓扑结构及属性可有效分析网络供气失效风险传播情况[5]。国内外对天然气管道风险问题进行了许多研究。

目前，针对天然气管道的风险评估主要采用事故概率的风险评估模型[6]以及管道风险指标评价方法，其中，评估管道潜在危害的方法包括使用AHP-TOPSIS综合评价方法来确定风险因素的影响[7]和基于云模型理论评估管道风险等级[8]。但是，这些方法存在一些局限性，如风险源识别不全面、无法考虑外部因素等问题。此外，在研究管道脆弱度方面，刘海云等[9]采用网络平均路径长度、介数、连通度来评估网络节点的脆弱度。WANG W C等[10]基于网络中心性指标、最大连通性指数、边失效率评估管道网络的脆弱度。其中，采用连通度作为管道网络的脆弱度评价指标，只考虑了节点和边的数量。相比之下，网络效率可反应网络中节点之间信息传播的速度和效率，是一个全局指标，而不仅仅反应某个节点或者局部子图的性能。因此，用网络效率作为管道脆弱度评价指标之一可以更全面地反映网络的连通性和风险传播问题。同时，在研究管道网络拓扑以及网络节点重要性评估上，YE H等[11]基于复杂网络理论研究天然气管道网络的拓扑结构，并根据天然气管道网络整体拓扑结构特征研究了天然气网络的特征，有助于相关部门实施分级防控。DU Y X等[12]将TOPSIS首次应用于识别复杂网络中的影响节点。通过考虑几种不同的中心性度量作为复杂网络的多属性在TOPSIS中的应用，得到每个节点的节点重要性排序。

本文运用负载容量级联风险模型，得到网络节点在随机破坏与基于熵权TOPSIS方法的蓄意破坏下每个节点的风险传播率，同时，利用管道网络平均路径长度、节点介数、以及网络效率重新定义网络节点脆弱度，计算网络每条边的风险传播强度。并基于节点风险传播率与传播强度提出了网络风险路径传播方法，运用于上海市天然气管道运输网络，从而找出管道网络在不同破坏策略下的风险传播路径，为管道安全管理提供决策支持。

1 天然气管道节点重要性评估模型

1.1 天然气管道运输网络结构

天然气管道运输网络节点由LNG接收站、储气库、调压站组成，可以表示为

G=（V，E）（1）

其中，V为天然气管道运输网络中管道运输节点的集合，E为网络节点与节点之间的连接关系，并以Bm×n=（bij）m×n，表示网络拓扑图的邻接矩阵。

1.2 天然气管道网络节点重要性评估

将网络节点度、聚类系数、接近中心性、介数中心性和管道气压强作为评价指标，基于熵权法修正的TOPSIS模型[13]对天然气管道供气网络节点的重要性进行综合排序。

步骤1 根据指标数据aij（i=，3，…，m ; j=，3，…，n，i为评价目标数、j为指标数），建立原始的评价指标体系矩阵Amn：

Amn=a11a12…a1na21a22…a2nam1am2…amn（2）

判断输入的矩阵中是否存在负数，如果有则要重新标准化到非负区间。由于天然气管道网络的评价指标中不存在负数，因此，对标准化的矩阵记为Z～ij，计算公式为

Z～ij=aij/∑ni=1a2ij（3）

步骤2 计算概率矩阵P，其中P中每个元素Pij的计算公式为

Pij=Z～ij∑mi=1Z～ij（4）

步骤3 计算每个指标的信息熵，并计算信息效用值，并归一化得到每个指标的熵权，信息熵的计算公式：

ej=－（Ln（m））－1∑mj=1Pijln（Pij）（5）

步骤4 根据各个指标的信息熵计算出权重Wj，得到的权重构造加权规范化矩阵Rmn。

Wj=1－ejn－∑nj=1ej，Rmn=rijm×n=Wj×ij（6）

步骤5 计算最大值X+和最小值X－。其中X+为每个评价指标的最大值，X－为每个评价指标的最小值。

X+=r+ r+2，…，r+n=maxr1 r2 …，rn maxr12，r22，…，rn2，…，maxr1m，r2m，…，rnm

X-=，…，n=minr1 r2 …，rn minr12，r22，…，rn2，…，minr1m，r2m，…，rnm（7）

步骤6 计算各节点与最大值和最小值的贴近度Si，其中，0≤Si≤1，每个节点按照贴近度大小进行排序，值越大，节点越重要。

D+i=∑nj=1（rij－r+j）2，D－i=∑nj=1（rij－r－j）2，Si=D－iD－i+D+i（8）

2 天然气管道运输网络风险传播模型

2.1 节点初始风险负荷

节点介数为网络中所有最短路径中经过该节点的路径数目dij（i）占最短路径总数的比例，是衡量管道网络各节点风险信息传播的影响程度，将节点初始风险负荷Li（0）定义为节点介数B（i）：

Li（0）=B（i）=∑i≠j∈Ndij（i）dij（9）

2.2 最大极限风险值

当节点遇到火灾爆炸、自然灾害等风险事件时，抵抗这些突发事件破坏的承受风险值是有限的，只有经常进行设备维护与检修才能够提高该极限风险值。最大极限风险值容量Ci与风险初始负载Li（0）成正比：

Ci=（1+α）Li（0）（10）

其中，α极限系数（α>0），通过调节极限系数α的大小可以控制节点风险负荷。

2.3 随机破坏与蓄意破坏策略

2.3.1 蓄意破坏

蓄意破坏描述的是一个针对网络节点的破坏过程，该过程按照网络节点的TOPSIS得分值排序进行破坏，并将受到破坏的节点状态从“正常”转变为“失效”。在这个过程中，破坏节点的数量逐步增加，直到网络中不存在任何“正常”节点时停止破坏。

2.3.2 随机破坏

随机破坏是在网络拓扑结构中，随机选取若干节点进行破坏，破坏操作导致选取的节点从“正常”状态转变为“失效”状态，失效节点不再承担原有的风险负载，而是按照负载重分配规则由其他正常节点进行分担，直至该“失效”节点不再向相邻节点扩散。

2.3.3 风险负载的重分配

管道节点受到外部活动破坏，会暂停运行成为失效节点，这些失效节点导致节点自身的风险负载容量超出，超出的风险负载会按照一定的分配机制分配到邻居节点，邻居节点接受来自失效节点分配的风险负载，加上自身的初始风险负载，导致其超出自身的风险承受能力，从而成为隐患风险点。假设相邻节点分担的负载大小为ΔLi→j，根据上述负载分配比例便可计算ΔLi→j[14]。

ΔLi→j=Li·Fj=Li·Cj－Lj∑vη∈Γi（Cη－Lη）（11）

式（11）中，Fj为相邻节点分担失效负载的比例，C为节点的容量，L为节点的负载。i为失效节点，j为i节点的相邻节点，而Cj表示当节点i失效时，与失效节点i相邻的节点j的容量。Lj则表示当节点i失效时，与失效节点i相邻的节点j的负载。∑vη∈Γi（Cη－Lη）表示节点i的所有相邻节点可容纳的负载和，此时处于“失效”状态节点的负载需要全部分散到相邻节点。如图1所示，当某一节点发生失效时，产生的风险会向邻居节点传播，造成一定的风险隐患，严重时会导致节点暂停工作，影响用户的供气。

2.4 网络级联风险传播率

2.4.1 节点风险传播率

管道节点的风险负载重分配导致周围邻居节点的风险负载随之发生改变，需重新判断该邻居节点的li与Ci的大小关系。这种关系与节点的风险负载能力和初始风险负载密切相关。管道拓扑网络中某节点的失效引起网络级联风险后，节点的风险失效率pi[15]为

pi=0，li<Ci

（li－ci）/2Ci，Ci≤li≤2Ci

Ci<li（12）

其中，li为网络级联级联后的节点负载，Ci为最大极限风险值容量。

网络的风险传播概率由节点风险失效率和节点度决定，风险传播率为

Qi=pi·DiDmax（13）

其中，Di为节点度，节点的度越大，传播能力越大。网络节点风险传播率可以直观地呈现天然气管道运输网络在遭受突发事件干扰后造成的损失程度，Dmax为网络中节点度最大的值。

2.4.2 节点失效风险传播计算步骤

1） 输入拓扑网络的邻接矩阵。2）初始化网络，计算节点介数和节点容量。3）根据破坏策略，在网络中删除失效节点。4）将失效节点的风险负载重分配到邻居节点，如果邻居节点风险负载大于节点本身的风险容量，则负载重分配，直到级联风险失效结束，计算网络效率与节点风险失效率。

2.5 天然气管道拓扑网络的风险传播强度

2.5.1 节点脆弱度

节点脆弱度M是衡量网络连接边风险传递脆弱程度的指标[9]，与网络平均路径长度K、节点介数Bi以及网络效率E相关，节点脆弱度为

Mi∈（ n）=Ki·BiEiMAX（14）

其中，Ki为移除节点i后网络的平均路径长度，Bi为节点介数，Ei为移除节点i后的网络效率。MAX为节点脆弱度的最大值。网络效率E[16]是网络中两个节点之间距离倒数的平均值，其大小反映了整个网络的传输效率，网络效率越大，说明网络中节点间连通性越好，其表达式为

E=1N（N－1）∑i≠j1dij（15）

其中，1dij为节点i与节点j之间的网络效率，dij为节点i与节点j之间的最短路距离。

2.5.2 级联风险传播强度

节点风险传播概率越高，越容易出现安全隐患。网络的风险传播强度与节点风险传播率Q[17]和脆弱度M相关。综上所述，节点风险传播强度Ri与边的传播强度Rij为

Ri=Qi·Mi（16）

Rij=Qi·Wi+Qj·Mj2（17）

2.5.3 最大风险传播路径确定

在天然气管道网络G = （V， E）中，V为节点集合，E为边集合。其中给定一个风险源节点i，风险传播开始于风险源节点i，并沿着与风险源节点相邻的最大风险传播度的节点和边进行。在每个相邻节点，风险继续沿着最大风险传播强度的相邻节点和边传播。计算每次传播过程中的风险传播强度总和，直到传播到边风险强度远远小于源节点连接边的风险传播强度时中止。最终，传播强度最大的路径就是网络中的最大风险传播路径。在每次传播过程中，计算风险传播强度之和：

T（i）=∑j∈V，i∈VRmax（i，j）（18）

T（i）为从源节点i开始的风险传播过程中每次传播的风险传播度之和。Rmax（i，j）为从节点i到节点j 中每条边的最大风险传播度。最后，具有最大传播强度的路径Hi－j，…，－n可以通过公式（19）确定。

Hi－j，…，-n=Maxi∈VT（i）（19）

3 案例分析

3.1 天然气管道运输网络实例

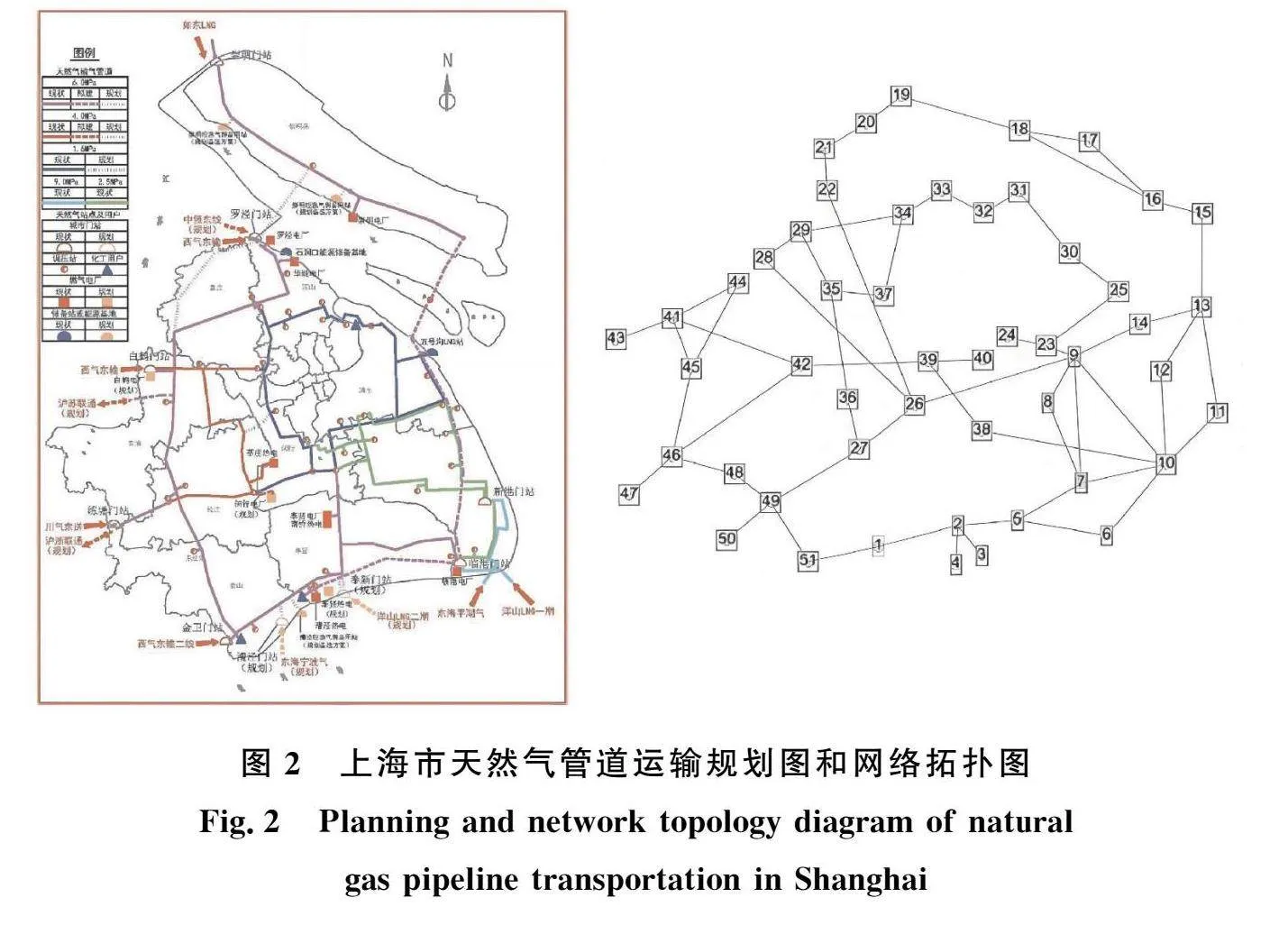
为验证模型的可行性，将上海市天然气管道网络作为实例进行分析。在Gephi软件中输入网络的邻接矩阵得到的网络拓扑图如图2所示，其拓扑结构是基于上海市“十三五”天然气主干网和重点设施规划所建立。

3.2 网络节点重要性评估

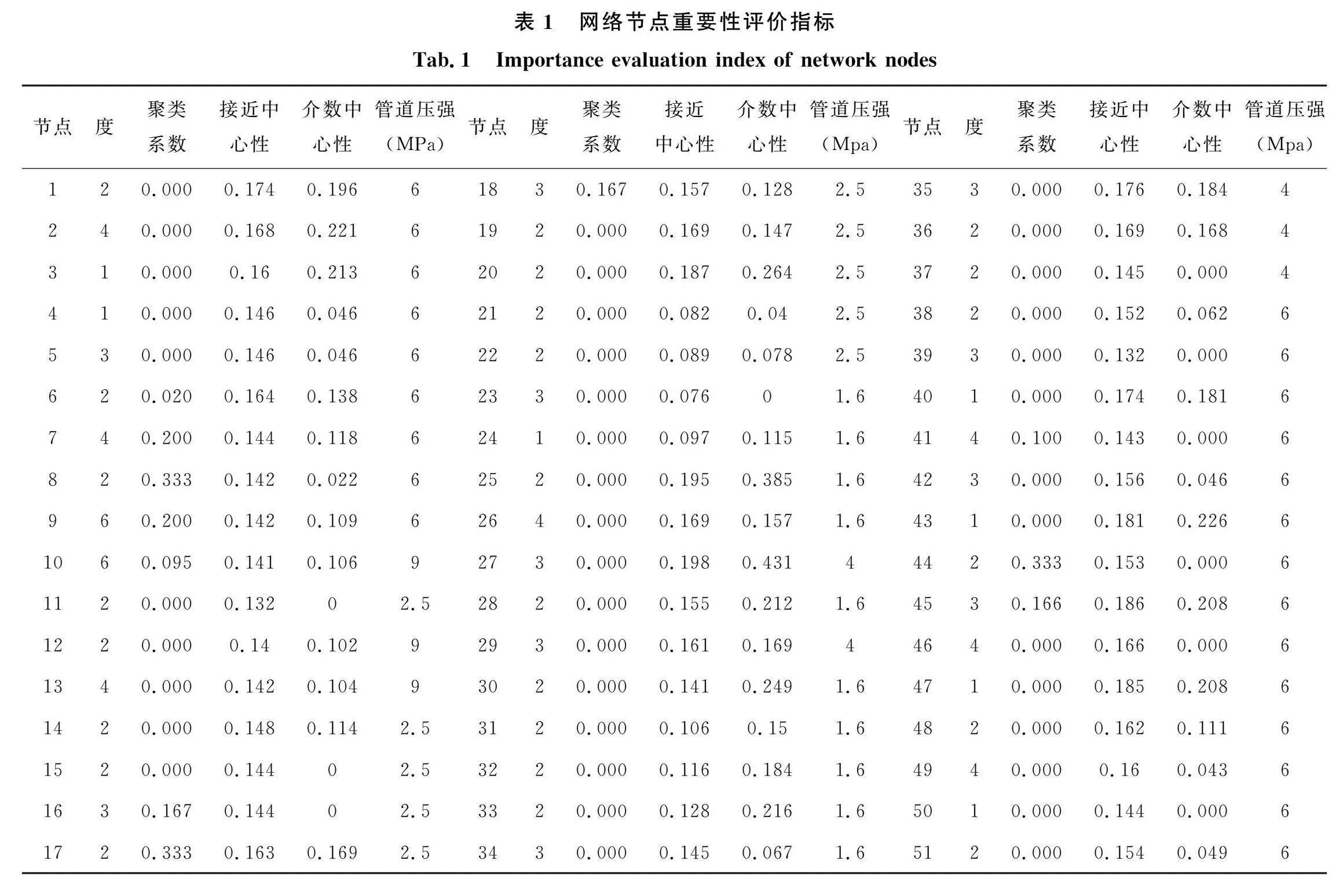
选取网络特征指标和管道气压作为节点重要性评价指标。

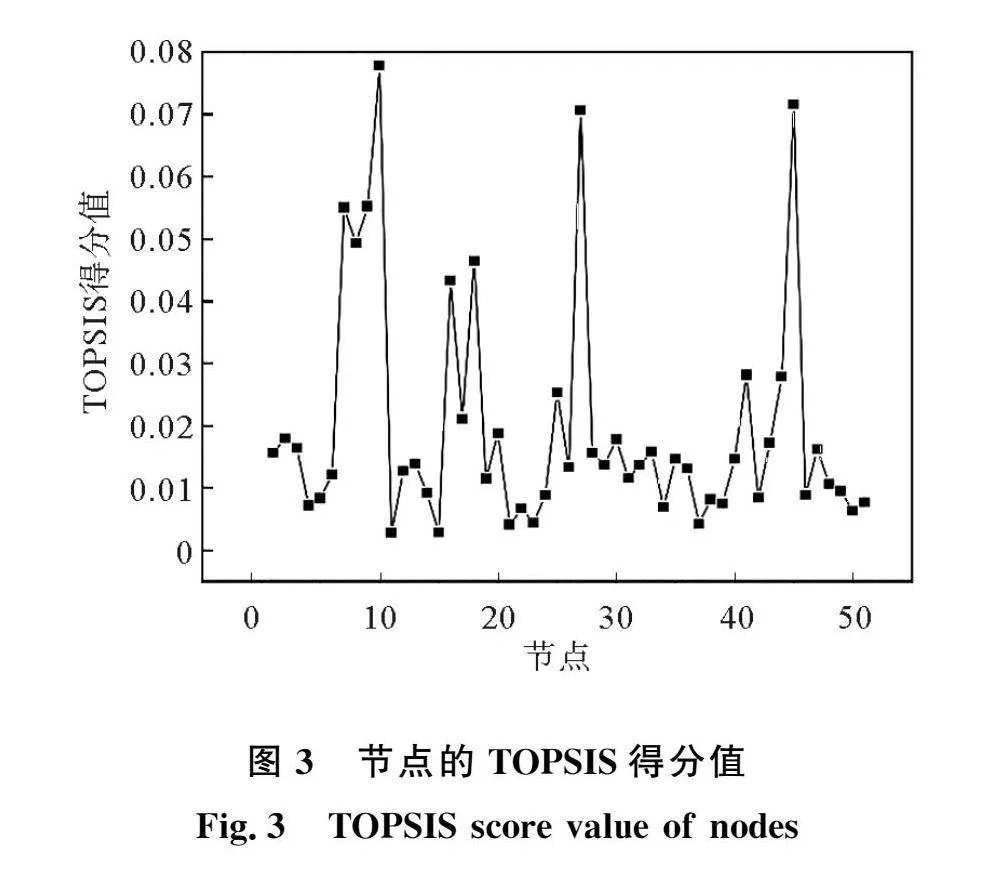
根据表1各指标采用基于熵权法修正的TOPSIS评价方法，利用matlab软件计算可知网络中每个节点的TOPSIS得分值如图3所示。表中节点10得分值最高，表明该节点在网络中最重要，其次是节点45，节点按重要度排序为10、45、27、9、7、8、18、16、41、44，…，11。

3.3 网络风险节点传播强度分析

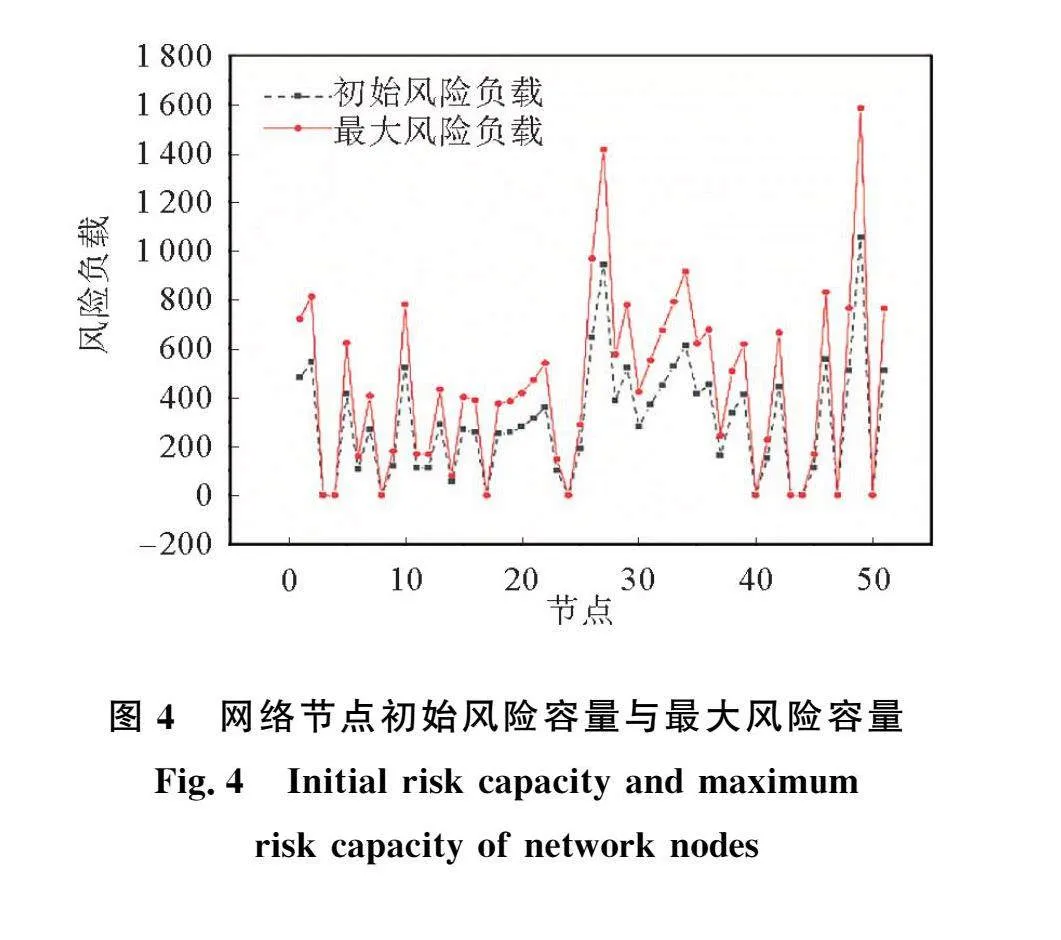
3.3.1 初始风险容量与最大风险容量

通过式（9）～（10），取α=0.5[15]，得到网络中的各个节点在初始状态下具有确定的风险负载和最大风险负载承受能力。如图4所示，节点的最大风险负载与其初始风险负载容量差距越大，说明该节点在网络中位于经过的最短路径数最多的位置，因此，被破坏的节点产生的风险信息最容易传到该节点。如果节点的初始风险负载为零，则该节点的介数为零，说明网络中的最短路径不会经过该节点，因此该节点的风险较低。

3.3.2 随机破坏与蓄意破坏

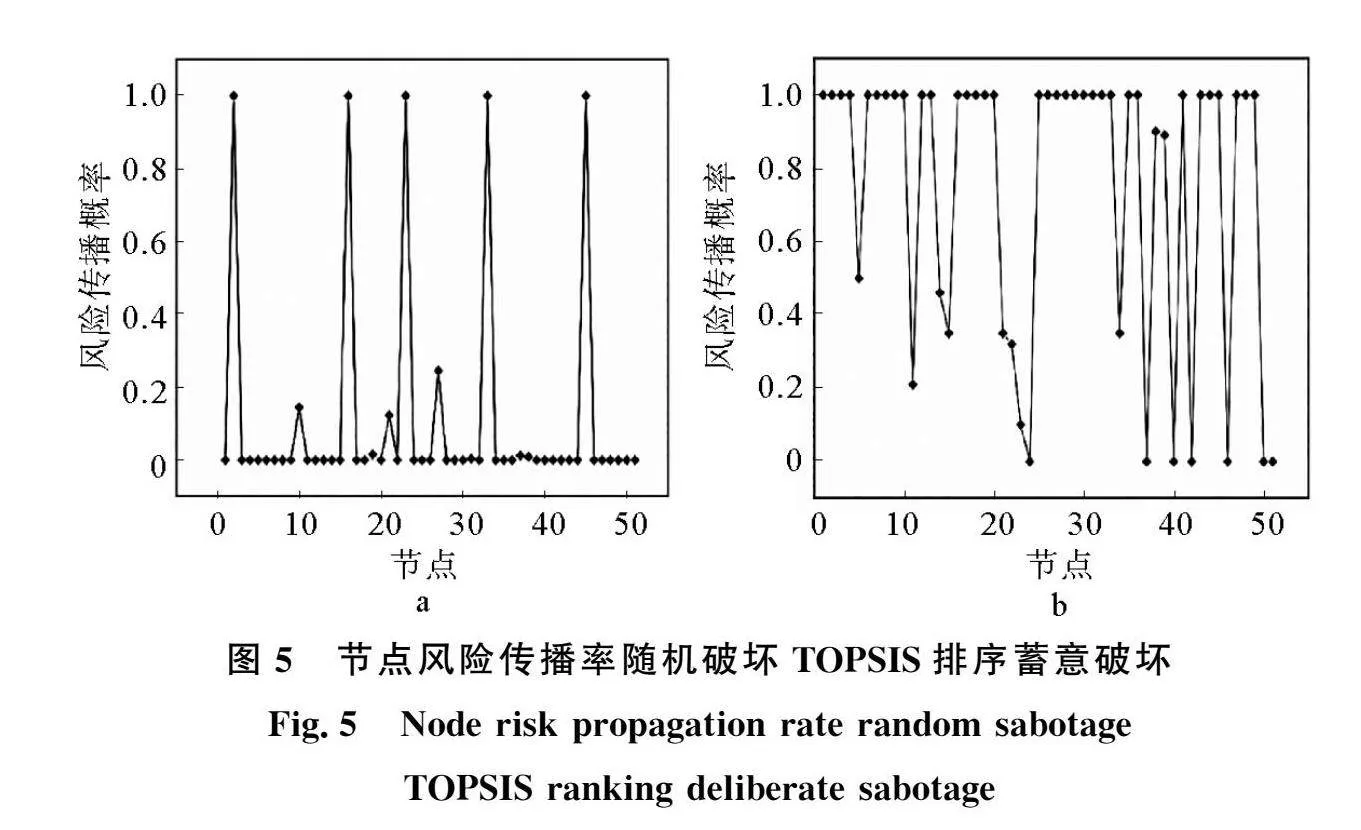
通过式（11）～（13）得到基于TOPSIS排序的蓄意破坏和随机破坏的网络节点失效率，如图5a和b所示。图5中，风险传播概率为1的节点是被破坏的节点和由于风险的相互传播而导致该节点成为的隐患节点。风险传播率在0和1之间的节点表示网络中其他节点遭到破坏时可能会受到一定的风险概率，节点为0的点表示网络中其他节点的失效而导致该节点存在较少的风险。在图5a中，大多数节点风险传播概率为0，只有少数节点的风险传播概率为1，这是因为管道网络在随机破坏的情况下，管网的风险传播较低。相比之下，在图5b中，大多数节点的风险传播概率为1，只有一小部分节点的风险传播概率为0，这是由于基于TOPSIS排名的蓄意破坏所导致的风险的快速传播。

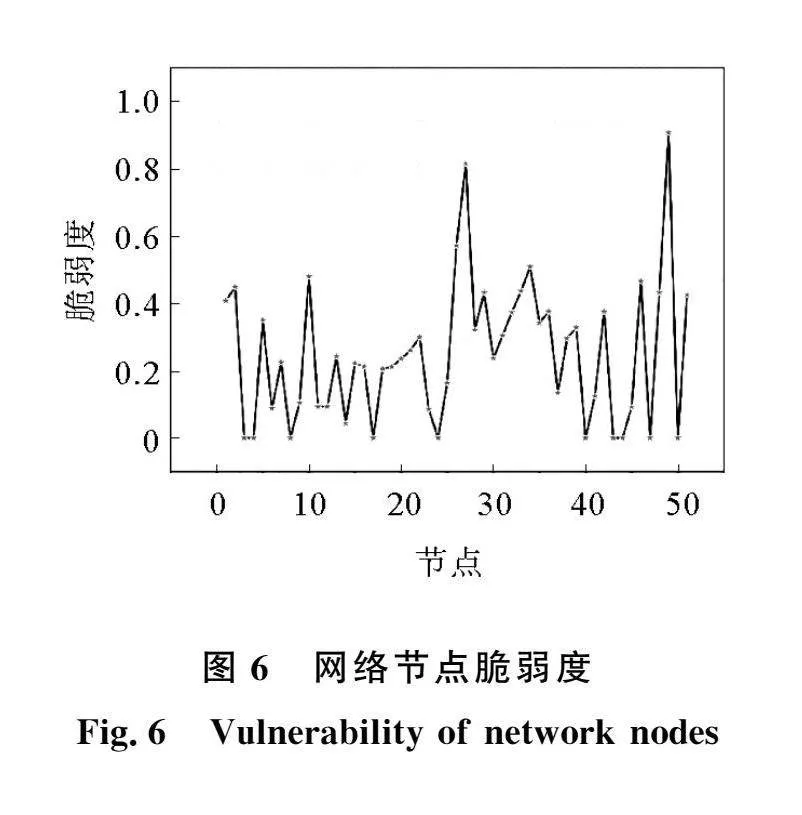
3.3.3 节点脆弱度计算结果

脆弱度是节点在网络中传递风险的程度，脆弱度越高，节点对网络风险的传播影响就越大。根据式（14）～（15），得到网络中各节点的脆弱度如图6所示。当某个节点的脆弱度为0时，说明无论该节点的连接是否被删除，都不会导致其他节点失效从而传播风险。

3.3.4 风险传播度计算

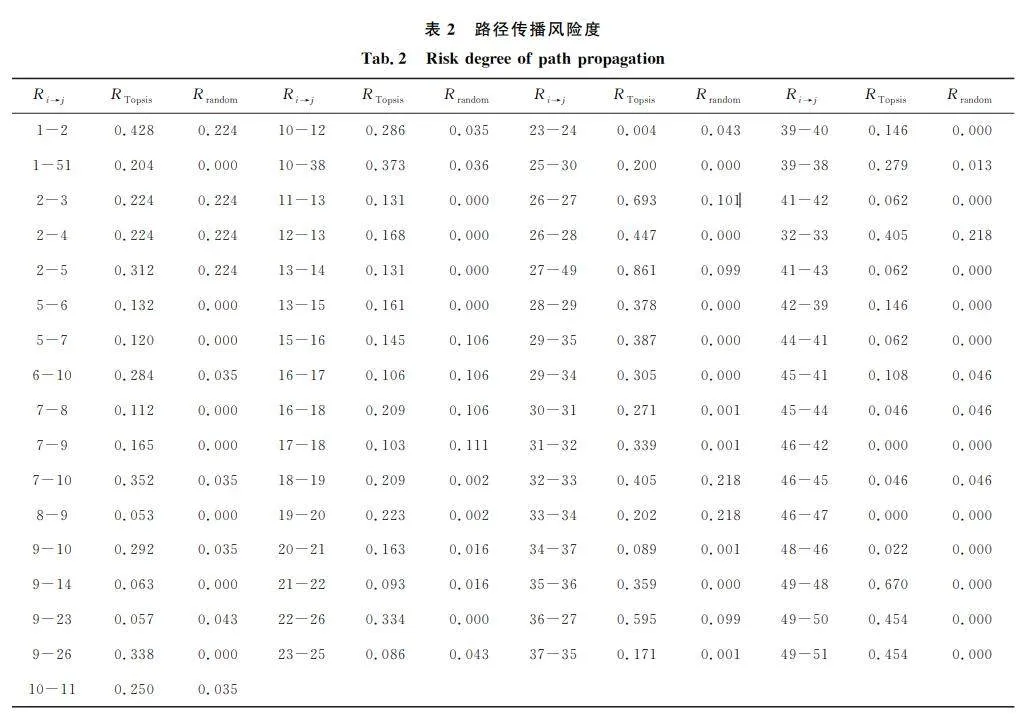
通过式（16）～（17）得到天然气管道拓扑网络各路径的传播风险度，如表2所示。显然，网络中每条边上的蓄意传播强度RTopsis都大于随机传播强度Rrandom，该现象的发生是由于蓄意破坏是人为有目的性地选取网络中的关键节点进行破坏。根据级联风险模型，这种破坏对网络造成的伤害更大。而随机破坏则包括大多数的自然灾害、人的不安全施工行为、设施年久维修，其对网络的破坏相对较为随机和分散，造成风险传播的可能性相对较低。

3.4 风险传播路径分析

当管道网络中某个节点失效后，根据式（18）～（19），风险传播路径是按照风险度高传到风险度低的节点，由此得到蓄意破坏和随机破坏的级联传播风险度最高的路径如表3所示。

由表3可知，蓄意破坏失效传播风险度总和远远大于随机破坏，两种风险传播重叠路径为6910。且蓄意破坏形成的风险传播路径经过的大都是储备站、能源基站以及化工厂等关键设施附近，一旦该路径上某节点发生失效，对上下游的节点影响较大，从而影响大面积用户燃气的使用，严重可造成人员伤亡。不管是蓄意破坏还是随机破坏，两种破坏策略形成的风险传播路径都需要重点监控与维护。对于蓄意破坏，应该加强对关键节点周围区域的巡逻和监控，及时发现和处理异常情况。对于随机破坏，应该加强设施的维护和管理，确保设施的安全运行，减少设施老化和不安全施工等因素对网络的影响。

4 结论

本文以上海市天然气供气网络为例进行实证分析。研究结果表明，供气网络风险传播可以提供一个新的方法来解决管道布局带来的供气节点失效风险传播问题。并提出一种基于复杂网络理论的网络风险路径传播方法，并用于模拟破坏天然气管道供气网络的重要节点。得到结论：两种破坏策略下，蓄意破坏得到拓扑网络风险传播度最大的路径，且蓄意破坏的网络风险传播度要大于随机破坏的网络风险传播度，表明蓄意破坏对网络造成的影响更大；两种破坏策略下的网络风险传播路径有重叠部分，意味着重叠部分的路径更容易受到来自邻居节点的影响。其中包括节点脆弱度较大以及TOPSIS得分值最大的节点；蓄意破坏下得到的风险传播路径为125610926274948，表明蓄意破坏对天然气管道拓扑网络的风险传播具有较大的影响，需要采取有效的措施加以防范和管理。同时，随机破坏下的风险传播路径为61092324，需要加强设施的维护和管理，以保障网络的稳定和安全。两种破坏下的叠加路径为6109，需重点监控与维护。未来的研究可以进一步深入探讨网络破坏的机制和规律，为网络安全管理和维护提供更有效的参考和指导。

参考文献：

[1]FARZANEH-GORD M， RAHBARI H R. Response of natural gas distribution pipeline networks to ambient temperature variation[J]. Journal of Natural Gas Science and Engineering， 2018， 52： 94105.

[2]BARIHA N， MISHRA I M， SRIVASTAVA V C. Hazard analysis of failure of natural gas and petroleum gas pipelines[J]. Journal of Loss Prevention in the Process Industries， 2016， 40： 217226.

[3]彭开和. 基于十堰市“6·13”重大燃气爆炸事故的城市天然气管道事故原因分析及对策研究[J]. 工业安全与环保， 2022， 48（5）： 2022.

PENG K H.Study on the causes and countermeasures of urban natural gas pipeline accidents based on the “June 13” gas explosion accident in Shiyan[J]. Industrial Safety and Environmental Protection， 2022， 48（5）： 2022.

[4]张之刚， 常朝稳， 韩培胜， 等. Risk Rank：一种网络风险传播分析方法[J]. 重庆大学学报， 202 44（9）： 132138.

ZHANG Z G，CHAO Y G，HANG P S，et al.Risk rank：an analysis method of network risk propagation[J]. Journal of Chongqing University， 202 44（9）： 132138.

[5]王冬. 复杂网络的拓扑结构对传播动力学的影响研究[D]. 哈尔滨： 哈尔滨工业大学（深圳校区）， 2021.

WANG D.Research on the influence of topological structures of complex networks on propagation dynamics[D]. Harbin： Harbin Institute of Technology（Shenzhen），2021.

[6]BAI Y P， WU J S， REN Q R， et al. A BN-based risk assessment model of natural gas pipelines integrating knowledge graph and DEMATEL[J]. Process Safety and Environmental Protection， 2023， 171： 640654.

[7]WANG X， DUAN Q Q. Improved AHP-TOPSIS model for the comprehensive risk evaluation of oil and gas pipelines[J]. Petroleum Science， 2019， 16： 14791492.

[8]田思祺， 高鹏， 刘畅. 基于云模型的跨越管道综合风险评估[J]. 油气储运， 202 40（7）： 822827.

TIAN S Q，GAO P，LIU C. Comprehensive risk assessment of crossover pipelines based on cloud model[J]. Oil & Gas Storage and Transportation， 202 40（7）： 822827.

[9]刘海云， 韩晓松， 翟振岗， 等. 基于复杂网络的燃气管线破裂灾害链风险分析[J]. 中国安全生产科学技术，2020，16（9）：3742.

LIU H Y，HAN X S，ZHAI Z G， et al. Risk analysis on rupture disaster chain of gas pipeline based on complex network[J]. Journal of Safety Science and Technology， 2020， 16（9）： 3742.

[10] WANG W C， ZHANG Y， LI Y X， et al. Vulnerability analysis of a natural gas pipeline network based on network flow[J]. International Journal of Pressure Vessels and Piping， 2020， 188： 104236.

[11] YE H， LI Z P， LI G Y， et al. Topology analysis of natural gas pipeline networks based on complex network theory[J].Energies， 2022，15（11）： 3864.

[12] DU Y X， GAO C， HU Y， et al. A new method of identifying influential nodes in complex networks based on TOPSIS[J]. Physica A： Statistical Mechanics and Its Applications， 2014， 399： 5769.

[13] CHEN P Y. Effects of the entropy weight on TOPSIS[J]. Expert Systems with Applications， 202 168： 114186.

[14] 高双. 级联失效下武汉市轨道交通网络抗毁性研究[D]. 武汉： 武汉理工大学， 2017.

GAO S.Research on invulnerability of Wuhan rail transit network[D].Wuhan： Wuhan University of Technology， 2017.

[15] WANG J W， RONG L L. A model for cascading failures in scale-free networks with a breakdown probability[J]. Physica A： Statistical Mechanics and Its Applications， 2009， 388（7）： 12891298.

[16] FU C Q， WANG Y， WANG X Y. Research on complex networks' repairing characteristics due to cascading failure[J]. Physica A-Statistical Mechanics and Its Applications， 2017， 482： 317324.

[17] WANG Z， HU Y Y， DONG R，et al. Determination of the risk propagation path of cascading faults in chemical material networks based on complex networks[J]. The Canadian Journal of Chemical Engineering， 202 99（s1）： S540S550.

（责任编辑 耿金花）