具有CDS的动态多层网络银行系统性风险研究

摘要： 美国次贷危机表明CDS对银行系统性风险有很大影响，但CDS如何影响银行系统性风险的机理还未明。因此，构建了一个具有CDS交互作用的动态多层银行网络模型，研究两种经济环境下的CDS对银行系统的双重影响。研究结果表明：经济平稳时期，CDS有风险吸收作用，降低银行系统性风险；经济波动时期，银行因CDS释放的超额风险资产会转变为新的系统性风险；CDS的规模与银行系统性风险呈负相关关系，且规模存在临界值。

关键词： 信用违约互换（CDS）；系统性风险；银企间信用风险；风险转移

中图分类号： F830；N94文献标识码： A

Investigating Banking Systemic Risk of Dynamic Multilayer Networks with CDS

TANG Miao， FAN Hong

（Glorious Sun School of Business and Management， Donghua University， Shanghai 20005 China）

Abstract：The subprime mortgage crisis in the United States shows that CDS significantly impacts banking systemic risk， but the mechanism of how CDS affects banking systemic risk is still unclear. This paper first constructs a dynamic multi-layer banking network model with CDS interactions to study the dual impact of CDS on the banking system in both volatile and stable economic environments. The results show that when the economy is stable， CDS has a positive absorption effect， which successfully transfers the risk and reduces the banking systemic risk; When the economy is volatile， the excess risk assets released by banks due to CDS are transformed into new systemic risk; the size of CDS is negatively correlated with the banking systemic risk and there is a critical value of size.

Keywords： credit default swap（CDS）; systemic risk; bank-firm credit risk; risk transfer

0 引言

2008年房地产贷款违约导致美国次贷危机爆发，使得全球金融系统陷入困境，并对实体经济造成了严重的负面影响。自此许多国家意识到银企间信用风险蔓延的严重后果，聚焦于企业对银行系统的信用风险冲击[1]。近年来，金融业发展步伐逐渐加快，银行与银企间通过多种业务联系建立起富有连通性的银企信用关联网络，这种错综复杂的网络有利于资金的合理有效配置，但当系统中的银行或企业遭受经济冲击陷入财务困境时，信用风险会迅速在网络中蔓延。因此，信用风险对银行系统性风险具有决定性作用。

目前对于银行系统信用风险的研究，主要着重于银行间、银企间的信用风险传染以及其对系统性风险的影响。银行间信用风险传染方面，Ladley[2]构建了银行间信用风险传染模型，发现信用风险冲击较小时，高水平的连通性可以降低银行系统性风险，相反，传染效应会被放大。Mitchener和Richardson[3]研究大萧条时期恐慌情绪致使银行间抽逃资金，银行间的信用网络放大了系统性风险，促使信贷收缩。Leventides等[4]研究了银行间的复杂网络结构以及信用风险传染，发现高连通性下的银行间网络为信用风险的蔓延提供渠道。此外，银企信用风险传染方面，Bargigli等[5]研究银企信用网络与系统性风险的传染问题，发现网络集中度与系统性风险存在因果关系。Catullo等[6]构建了银企信用网络模型，发现系统风险的蔓延与杠杆率和银企信用网络结构有关。Silva等[7]基于巴西银企数据研究了银企间的双向信用风险传染，发现银企间信用风险比银行间信用风险更具有传染性。

为对冲银行因信贷带来的信用风险，信用违约互换（Credit Default Swap，CDS）因其风险转移功能引发了银行业的关注和研究[89]。已有研究基于CDS的视角对银行系统中的信用风险进行了不同程度的探讨，并发现CDS对降低银行信用风险有正向积极的影响。Allen和Carletti[10]提出了银行与保险机构之间的信用风险转移模型，证明了CDS有助于银行释放其流动性。Wagner和Marsh[11]发现银行利用CDS风险转移功能与银行间市场信用风险共担相比，CDS风险转移功能更有利于银行系统的稳定。D’errico等[12]提出了分析CDS的风险转移网络框架，研究了CDS的风险转移和市场结构，证实了该网络结构有助于系统稳定。Thornton和Tommaso[13]发现CDS在欧洲银行样本中被用于监管套利，CDS在吸收信用风险的同时产生更高的资本回报。尽管CDS是行之有效的信用风险转移工具，但它也会给银行带来新的系统性风险。Brunetti 等[14]发现CDS有时也会丧失对银行间信用风险的吸收作用，导致更大风险在系统中蔓延。Al-Own等[15]认为系统性信贷危机时期，银行即使是出于对冲银行间信用风险的目的使用CDS，也可能产生意想不到的风险。Bo和Capponi[16]指出CDS虽然能够实现银行间信用风险的对冲，但同时CDS与银行之间也存在着交易对手信用风险。即信用风险超出CDS卖方的赔偿能力时，会导致信用风险在银行系统中的进一步扩散。Schuldenzucker等[17]提出了银行间债务违约互换模型，研究发现CDS给银行网络带来新的系统性风险，并且该网络因CDS带来的风险比银行系统内在的风险传染更为重要。

综上所述，现有文献在研究CDS或银行信用风险时，要么仅专注于银行间的单层网络描述银行间信用风险传染，或银企间的信用风险传染，没有引入CDS风险转移机制；要么分析银行在引入CDS机制后，仅单方面探讨CDS对银行间信用风险的风险转移作用或CDS为银行系统带来的新的风险。基于此，本文构建了一个具有CDS的动态多层网络框架，探讨CDS对银企间信用风险的缓释效应，以及CDS使银行释放的超额风险资产不能收回而产生的风险放大效应。与单一分析CDS对银行信用风险缓释效应或风险放大效应不同，本文全面分析CDS的双重影响在多重网络间的作用机理；有利于挖掘信用风险缓释工具与银行、企业间的内在关联，同时为合理运用信用风险缓释工具，防范系统性风险提供一定的参考。

1 构建具有CDS的多层银行网络模型

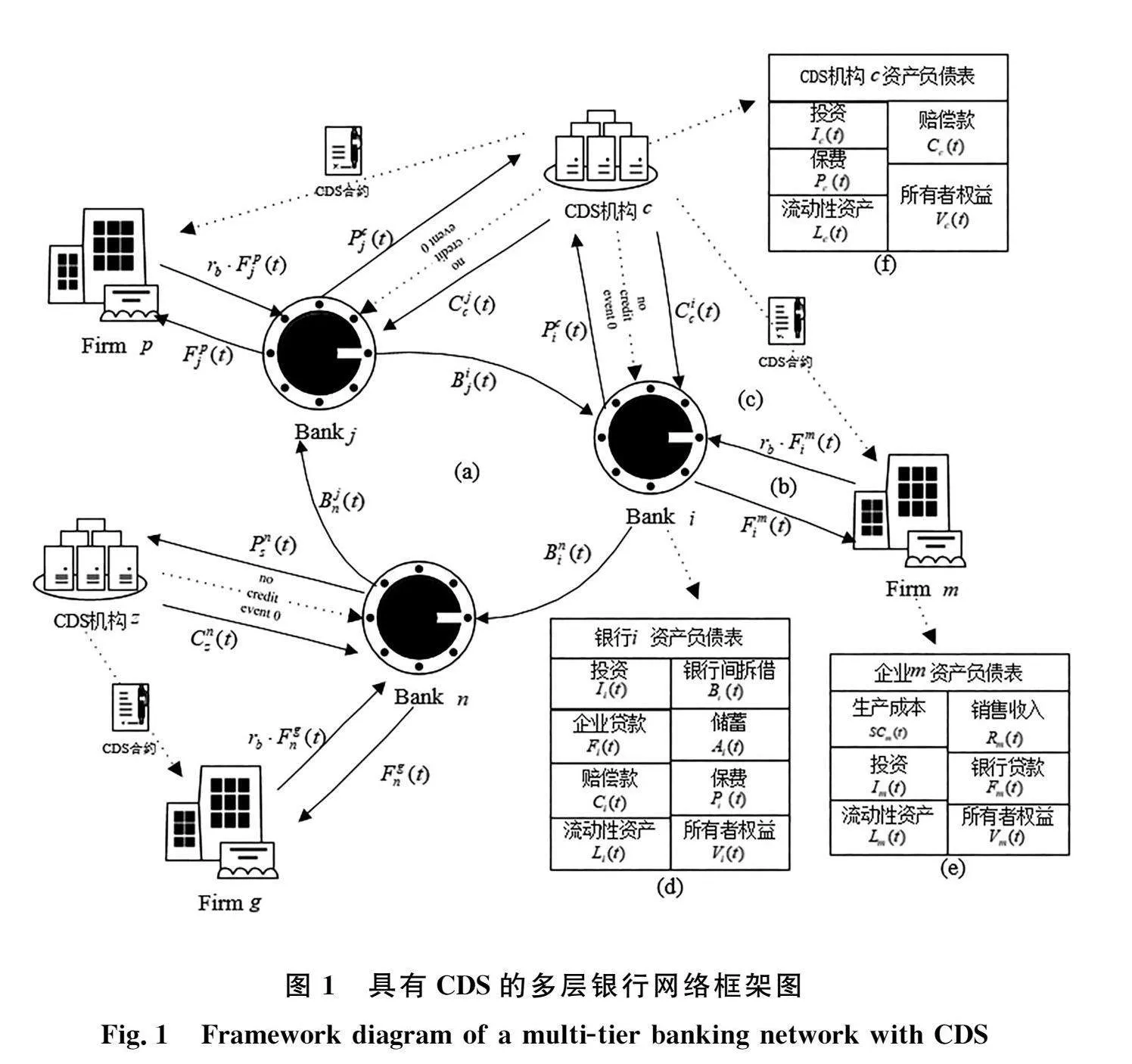
在银行网络中，各个不同规模的银行与企业之间通过借贷业务等关联关系，形成了一个复杂的信用关联网络[18]。虽然该网络有助于系统内部信贷资源分配，但也为信用风险的传播提供了渠道[7]。然而，CDS的风险缓释功能能够为银行的信用贷款提供保护，减少其风险加权资产的数量，并通过市场化交易形式将银行内部的信用风险转移。因此，本文考虑构建一个具有CDS的动态多层银行网络，以探究CDS在银行系统中的作用机制。具有CDS的多层银行网络框架，如图1所示。

1.1 银行间动态拆借网络

本文参考Iori[19]的研究，假设银行间拆借网络为随机网络，系统中存在N家银行，用矩阵U表示银行间的拆借关系，其中， Ui，j=1表示银行i与j之间存在同业拆借关系，Ui，j=0表示银行i与j之间不存在同业拆借关系。银行资产负债表随时间动态演化满足公式（1）：

Li（t－1）=Ai（t－1）+Bi（t－1）+Vi（t－1）－∑τs=1Ii（t－s）（1）

其中，Li（t－1）表示银行i在t－1时刻的流动性资产，Ai（t－1）表示银行i在t－1时刻的储蓄，Vi（t－1）表示银行i在t－1时刻的所有者权益，Bi（t－1）表示银行i在t－1时刻银行间拆借的资金总额。Bi（t－1）>0表示银行i的拆入金额，反之为拆出金额。∑τs=1Ii（t－s）是银行i在过去τ期的总投资。本文假设银行储户存款行为随机发生，那么银行i在t时刻的存款为Ai（t）=（1+σAη）A-，A-为储户存款均值，σA为存款波动的标准差，η～N（0，1）服从正态分布。

1.2 银企动态借贷网络

假设系统中有M家企业，企业m在t 时刻的流动性用Lm（t）表示。企业的主体行为包括生产经营以及投资。

1.2.1 企业生产经营

企业m在t时刻的产量受到财务约束，其生产函数表示为

Ym（t）=φ1Vφ2m（t）（2）

其中，φ1> 0<φ2< Vm（t）为t 时刻企业m的所有者权益。为遵循企业资本结构动态权衡理论，参考Gatti等[20]和Riccetti等[21]的研究，假设企业m生产产品以劳动力作为唯一输入参数，对每个企业而言Ym（t）=hm（t）/ξ，hm（t）代表劳动力数量，ξ>0。因此，在财务约束产量的情况下，劳动力可以写成公式（3）：

hm（t）=ξYm（t）=ξφ1Vφ2m（t）（3）

同时，企业m在t 时刻会对其生产的产品进行销售，其销售收入公式表示为

Rm（t）=μYm（t）（4）

其中，μ为销售价格，μ（t）=+σsη，为销售价格均值，σs为销售波动标准差。

1.2.2 企业投资

企业m在t 时刻若有流动性会进行投资，其投资满足公式（5）：

Im（t）=minmax0，Lm（t）+Rm（t）－SCm（t），ωm（t）（5）

其中，企业的生产成本SCm（t）=Φhm（t），Φ为劳动力价格，ωm（t）为企业m在t 时刻的投资机会，ωm（t）=m+σmη，m为企业投资均值，σm为企业投资波动标准差。

企业m在t 时刻可能面临资金缺口Qm（t）=max0，SCm（t）－（Lm（t）+Rm（t））。本文假设企业m会随机向某个流动性充足的银行发出借贷请求，如果银行i的流动性无法填补企业m的全部资金缺口，则剩余的部分资金缺口，企业m会继续向其他银行寻求帮助，直到企业的资金缺口被全部填补或银行市场中没有多余的流动性为止。那么流动性充足的银行i 在t 时刻可以贷给企业m的金额为

Fmi（t）=minχ·Li（t），Qm（t）（6）

其中，χ为银行准备借贷给企业的资金占自身流动性的比例。《巴塞尔协议》要求银行在贷款时满足监管要求，保证相应的资本充足率，则银行i需要为所有银企间贷款准备的资本储备金为CRi（t）=∑m∈MFmi（t）。此时，银行资产负债表的动态演化行为如（7）所示：

Li（t－1）=Ai（t－1）+Bi（t－1）+Vi（t－1）－∑m∈MFmi（t－1）－∑τs=1Ii（t－s）（7）

其中，∑m∈MFmi（t－1）为t－1时刻银行i向企业提供的贷款总额，其它符号的含义同上。

企业与银行发生借贷行为后，会定期向银行支付相应的利息。那么，银行i 在t 时刻有资金流动的变化，其流动性资产演化公式为

i（t）=Li（t－1）+（Ai（t）－Ai（t－1））－raAi（t－1）+rb∑τps=1∑m∈MFmi（t－s）+∑m∈MFmi（t－τp）+CRi（t－τp）+ρ∑τs=1Ii（t－s）+Ii（t－τ）－Di（t）－Ii（t）－βAi（t）－CRi（t）（8）

其中，Ai（t）－Ai（t－1）为t 时刻银行i 持有存款的变化；raAi（t－1）为支付给储户的利息，ra为存款利率；rb∑τps=1∑m∈MFmi（t－s）为t 时刻银行i向企业收取的贷款利息，rb为企业的贷款利率， τp为银企贷款周期；∑m∈MFmi（t－τp）为银行i在t时刻的贷款回收；CRi（t－τp）为银行i在t时刻回收的资本储备金；ρ∑τs=1Ii（t－s）为银行i在t 时刻过去τ期的投资收益，ρ为投资收益率；Ii（t－τ）为银行i 在t 时刻的投资回收；Di（t）为银行i 在t 时刻的分红；Ii（t）为银行i 在t 时刻的投资；βAi（t）为银行i 在t 时刻的存款准备金，β为存款准备金率，其它符号的含义同上。

1.3 具有CDS的动态银行网络

当有充足流动性的银行审批企业的贷款申请时，银行为了规避信用风险，会对申请贷款的企业进行风险评估，将风险集中度较高的企业贷款向CDS机构购买CDS合约，同时支付相应的CDS保费以换取与高风险贷款相称的赔偿。中国规定商业银行购买CDS合约后，可以将风险资产的权重降低80%。那么，银行i需要留存的资本储备金变为

CRi（t）=·1－80%∑m∈MFmi（t）（9）

CDS保费：银行i为了规避高风险企业m带来的信贷风险而购买CDS合约，所支付的保费可以表示为Pci（t）=λ·∑αs=1∑m∈φFmi（t－θs），φ为高风险企业集合，α=τp/θ为保费支付期数，θ为保费支付周期，λ为保费费率，∑αs=1∑m∈φFmi（t－θs）为t时刻银行i 需要缴纳CDS保费的贷款总额。

CDS赔偿：若在合约期限内与银行有借贷关系的企业发生信用违约事件，银行会获得CDS机构的赔偿款Cci（t）=（1+rb）∑τps=1∑m∈ΩtFmi（t－s）－λ·∑θs=1∑m∈ΩtFmi（t－s+1），Ωt为t时刻的违约高风险企业集合，∑τps=1∑m∈ΩtFmi（t－s）为t时刻银行i因企业违约而损失的本金，λ·∑θs=1∑m∈ΩtFmi（t－s+1）为CDS机构在t时刻扣除的未满支付周期的保费。若高风险企业没有发生信用违约事件，那么CDS机构不需要对银行进行赔付，Cci（t）=0。

具有CDS的银行系统中，银行i在t时刻的流动性可以用公式（10）表示：

Li（t）=Li（t－1）+（Ai（t）－Ai（t－1））－raAi（t－1）+rb∑τps=1∑m∈MFmi（t－s）+∑m∈MFmi（t－τp）+

CRi（t－τp）－Pci（t）+ρ∑τs=1Ii（t－s）+Ii（t－τ）+Cci（t）－Di（t）－Ii（t）－βAi（t）－CRi（t）（10）

1.4 具有CDS的银行网络动态演化流程

具有CDS的银行网络系统动态流程算法，具体分为以下几个步骤：

步骤1 计算银行流动性。根据式（8），计算银行i在t时刻的流动性i（t），如果银行i为银企间贷款购买了CDS，则银行i需要向CDS机构支付保费Pci（t），若债务企业发生违约，则银行i会收到CDS机构的赔偿Cci（t），此时银行流动性Li（t）=i（t）－Pci（t）+Cci（t）。

步骤2 区分临时债权、债务银行。当银行i的流动性Li（t）>0并且Bi（t－1）<0，则银行i为临时债权银行；当流动性Li（t）>0且Bi（t－1）>0，同时有Li（t）>1+rIBi（t－1），rI为银行间拆借利率，此时银行i会对上一期所有的债权银行进行还款，还清债务时的流动性Li（t）=Li（t）－1+rIBi（t－1），则银行i为临时债权银行。其他情况，银行i为债务银行。

步骤3 银企借贷与CDS合约。企业在生产经营的过程中会存在资金缺口，那么存在资金缺口的企业会向流动性充足的银行发起贷款申请。如果银行i将一部分流动资金贷给企业，那么银行i成为企业的债权银行，在t时刻贷出总金额为∑m∈MFmi（t），资本储备金为CRi（t），此时银行i的流动性Li（t）=Li（t）－∑m∈MFmi（t）－CRi（t）。债权银行收到企业贷款申请的同时，会对企业进行风险评估，如果企业资产负债率Sm>ψ时，企业风险较高，银行会选择向CDS机构购买CDS合约转移信用风险，CDS保费会在下一个支付周期于步骤2中计算。

步骤4 投资与分红。债权银行投资与分红，银行i的流动性更新为Li（t）=Li（t）－Di（t）－Ii（t）。

步骤5 银行间拆借。债务银行i随机向债权银行进行借贷，直到银行i能够有足够的资金来偿还上期的同业贷款1+rIBi（t－1），此时银行i所需的贷款金额为1+rIBi（t－1）－Li（t）。

步骤6 违约清算。如果债务银行i无法拆借到足够的资金，那么银行i违约并清算。

2 仿真分析

2.1 参数设置

为了探究CDS对银行系统的影响，本文在构建具有CDS的多层银行网络系统模型的基础上，参照Iori[19] 、Gatti等[20]和Riccetti等[21]的研究以及银行财务报表，采用蒙特卡洛方法对参数进行稳健性检验，结果稳定。假设系统中银行的数量为200，初始权益为300，初始存款为1 000；企业的数量为100，初始权益为500；CDS机构的数量为20，初始权益为300；仿真时间步T=500，其他参数如表1所示。本文根据银行平均倒闭概率来度量银行系统性风险。

2.2 经济稳定下CDS对银行系统性风险的影响

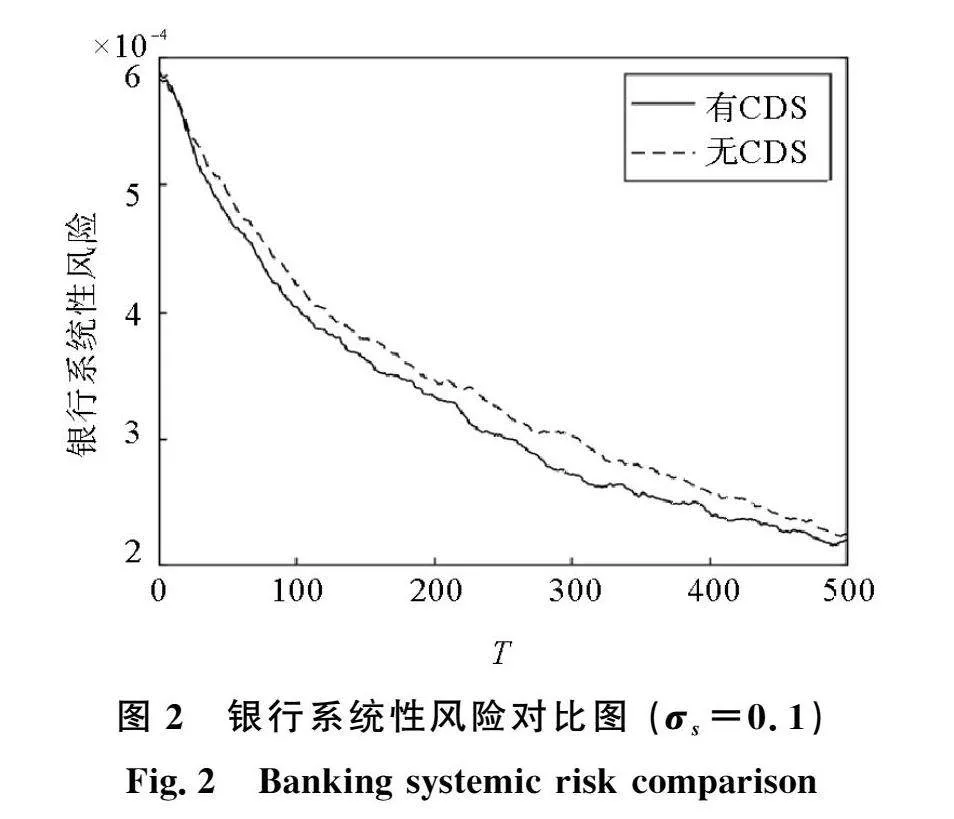
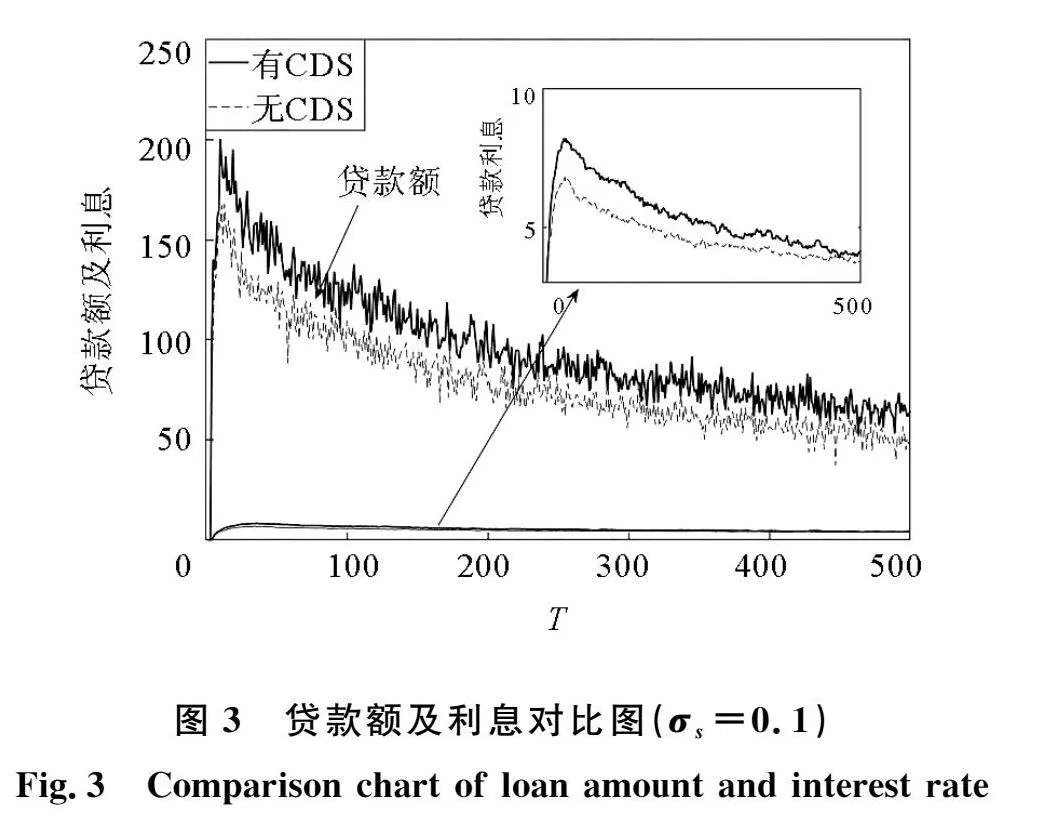
本文首先探究了经济稳定时期有无CDS的银行系统性风险变化情况（见图2）。在企业销售波动σs=0.1时，银行系统性风险随着时间步的变化逐渐降低，具有CDS的银行网络的系统性风险更低。CDS的存在致使银行更愿意为高风险企业提供贷款，在不增加风险的情况下增加了贷款利息收入，从而使银行系统更具有弹性。CDS的贷款额以及贷款利息收入，如图3所示。随着时间步的变化，两种网络的贷款额及利息都逐渐变小，但具有CDS的网络中各项数值均高于无CDS的网络。总的来说，CDS增加了系统的稳定性。

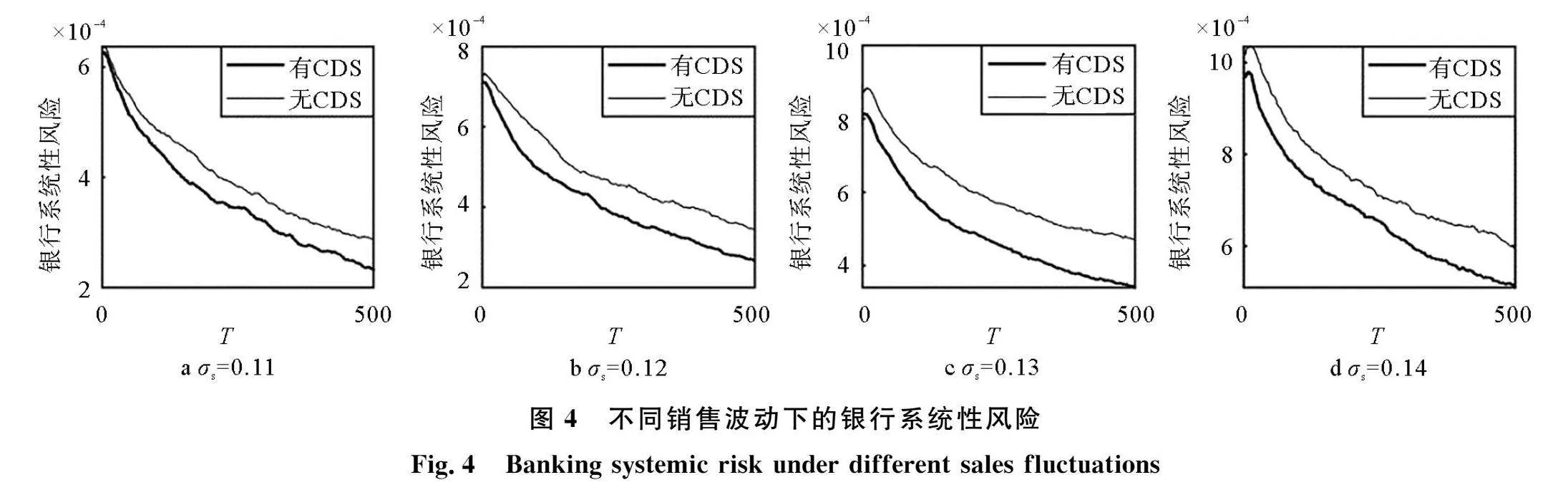
企业的销售波动会对银行系统有不同程度的影响，如图4所示。当销售波动在0.11至0.13内，销售波动与CDS的风险吸收作用呈正相关。当销售波动为0.14时，CDS对银行系统性风险的吸收作用减弱，部分CDS机构逐渐超出自身偿付能力，面临损失，这可能致使银行陷入困境。但与无CDS的银行网络相比，总体上还是吸收了银行系统性风险。

2.3 经济波动下CDS对银行系统性风险的影响

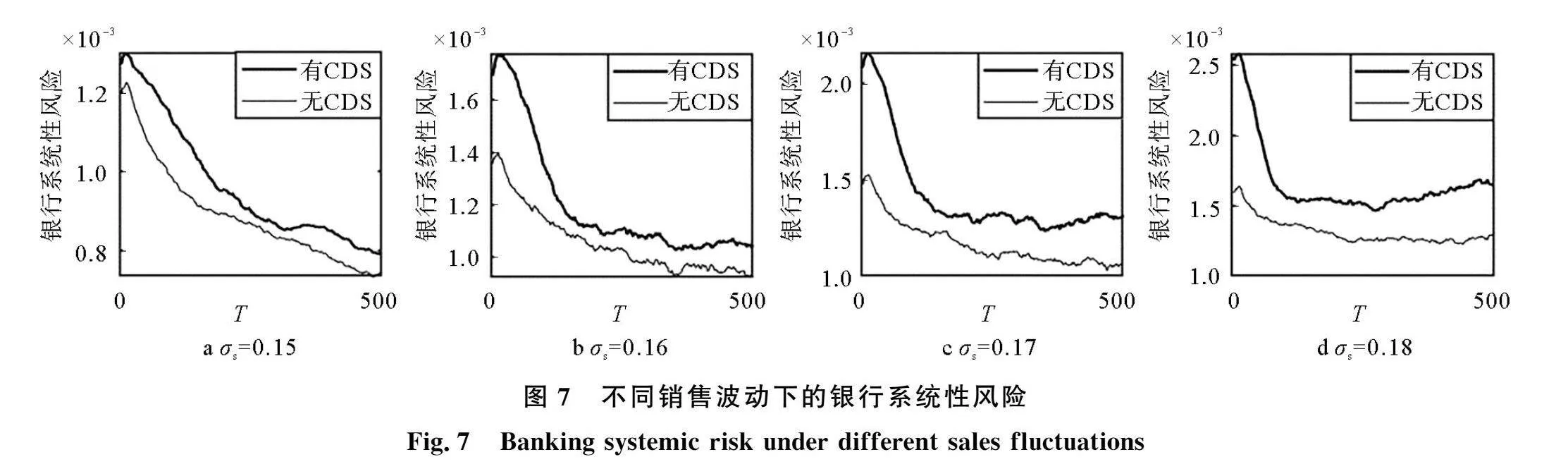
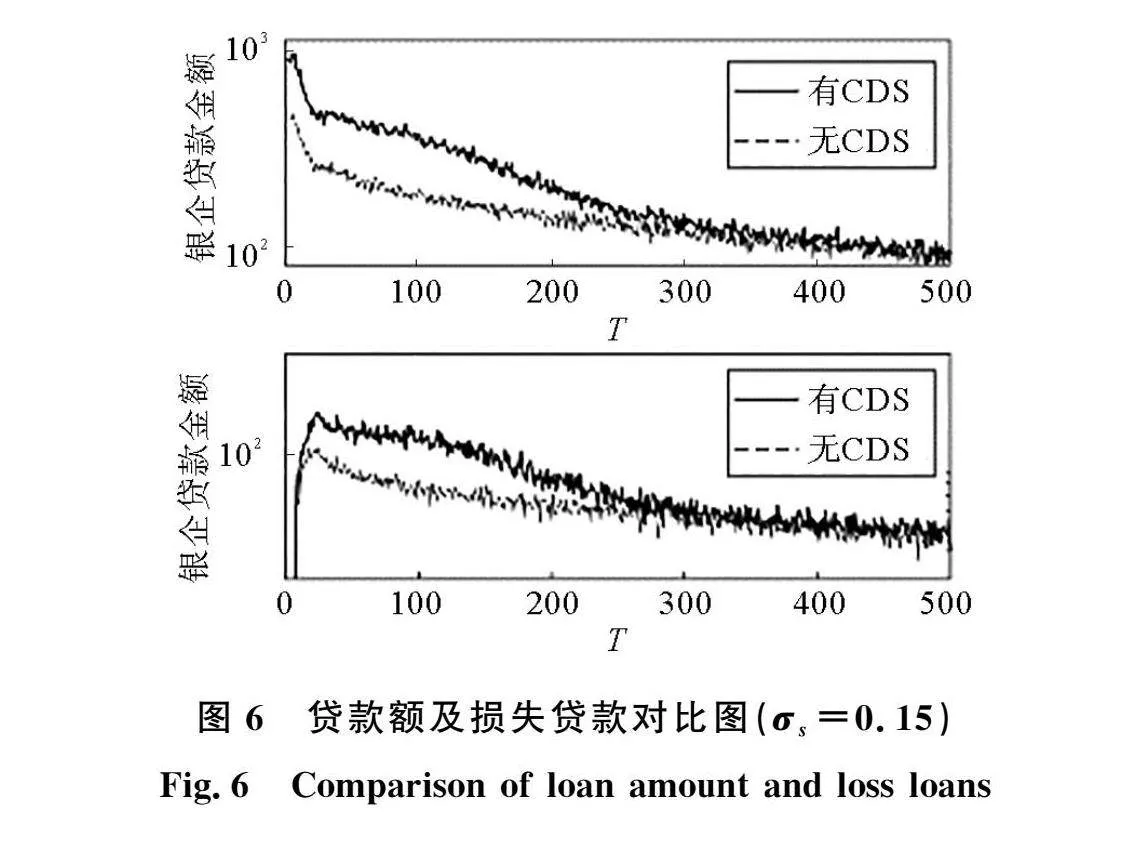
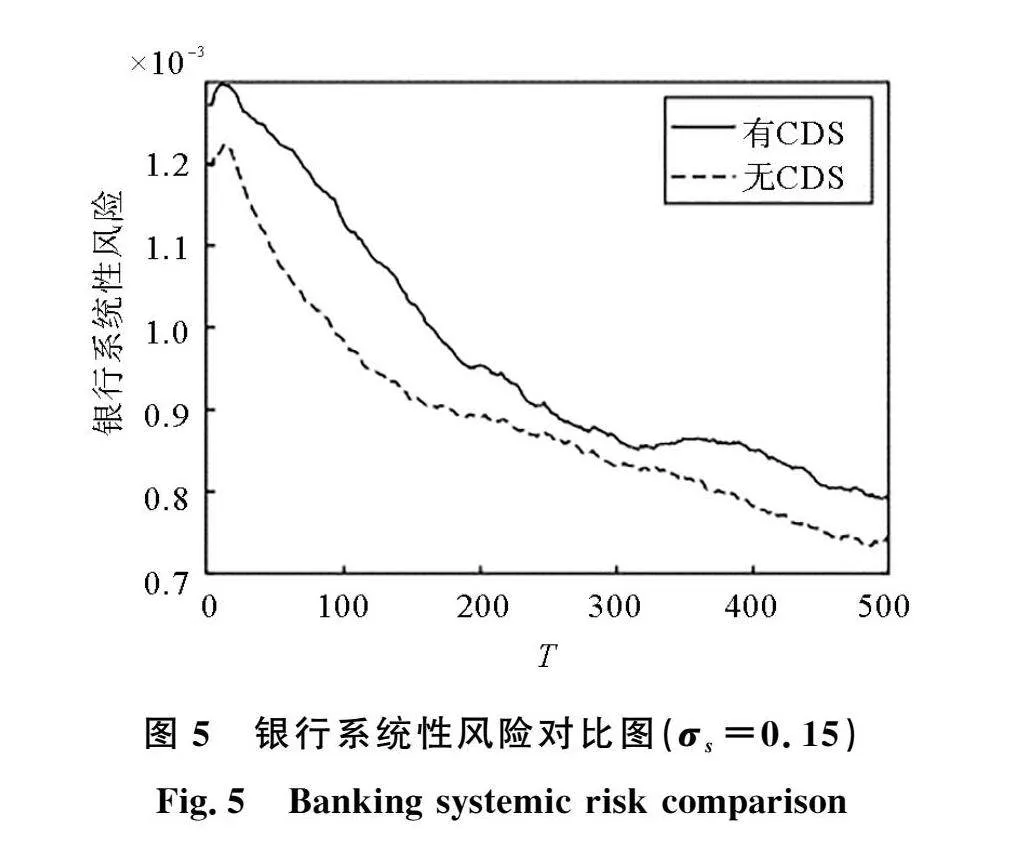
CDS虽然能够在经济稳定时期发挥风险缓释作用，但在经济波动时期，企业销售价格在市场政策、通货膨胀或紧缩等因素的影响下波动变大，CDS能否对银行系统起到积极正向作用还需要进一步研究。图5对比了企业销售波动为0.15时的有无CDS的银行系统性风险，发现具有CDS的银行系统性风险更大。CDS增加了银行对信贷资金的投入，但同时也会促使银行贷款质量降低。在严峻的经济形势下CDS机构面临大量的赔偿款，资不抵债触发违约。银行也因对交易对手风险的低估导致大量的贷款损失从而陷入困境，同时也可能给与之存在同业拆借的银行带来风险，使得风险在网络中蔓延。从图6也可以看出，具有CDS的银行网络中银行贷款额和损失贷款在前期均大于无CDS的银行网络中的各项值。因此，在宏观经济波动时期，如果CDS机构没有成功将银行的信用风险释放，那么CDS的存在不但不能吸收风险，反而会加剧银行系统的不稳定性。图7为不同销售波动下有无CDS的银行系统性风险的变化情况。企业销售波动越大，具有CDS的网络放大银行系统性风险的效应越大。另外，具有CDS的银行网络的风险值存在拐点，并且该拐点逐渐从系统中期的200步左右提前至100步左右，说明CDS机构因偿付能力不足发生违约的时间在不断提前。

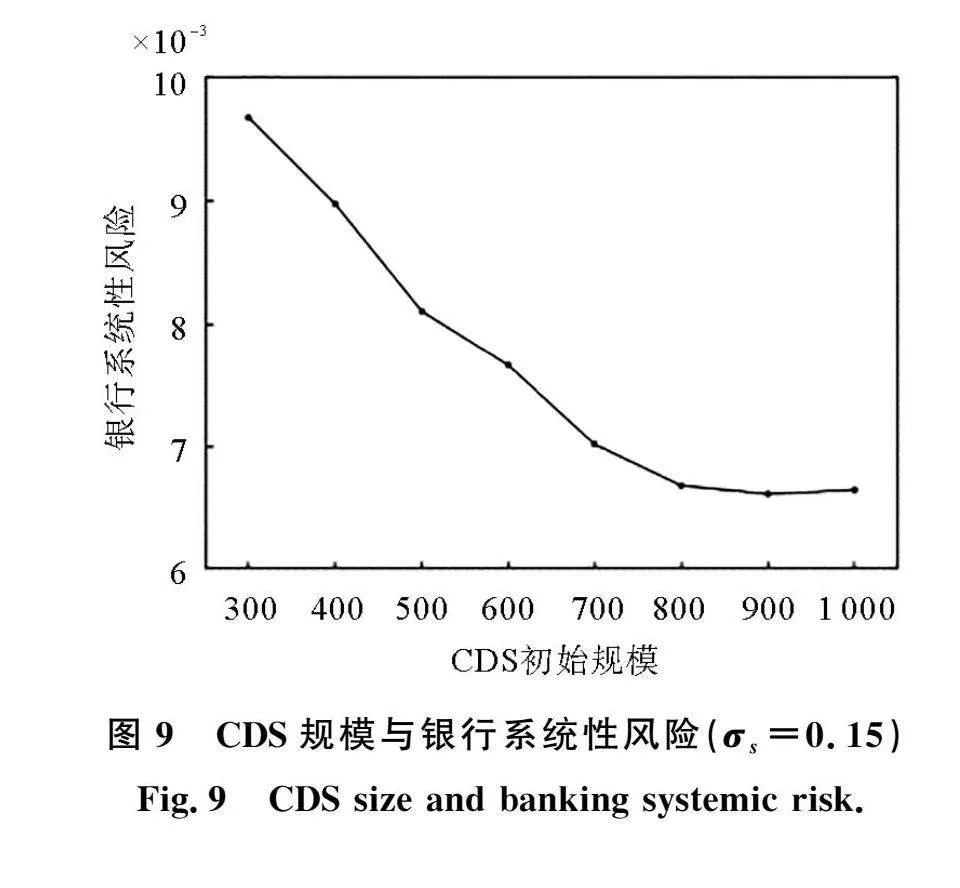
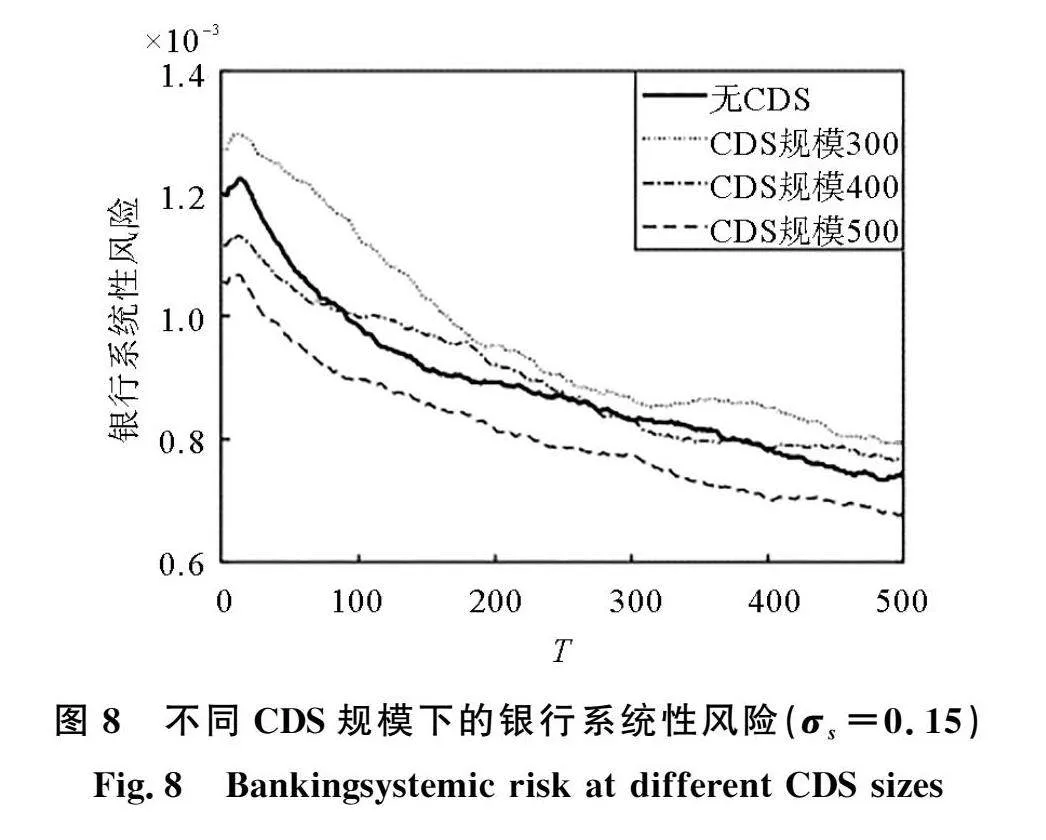
通过前文的分析，可以发现CDS机构的偿付能力与其规模以及风险的大小有关。在经济波动时期，CDS的规模与银行系统性风险的关系是一个值得探讨的问题。当企业销售波动为0.15时，不同CDS规模下的银行系统性风险动态演化情况，如图8所示。随着CDS机构规模的增加，银行系统性风险不断降低，当CDS机构的规模提升至500时，CDS对系统风险吸收作用再次显现。不同CDS规模与银行系统性风险的关系，如图9所示。当CDS规模大于800时，银行系统性风险基本不再变化。表明在一定的条件下，银行系统性风险的吸收对CDS机构规模有一定要求，且规模存在阈值。当CDS规模超出阈值时，CDS规模的变化对银行系统性风险影响不大。当CDS规模小于阈值时，CDS的规模与银行系统性风险呈负相关关系。因此，在银行与高风险企业发生借贷时，对CDS机构规模的考察也是很必要的。

3 结论

在金融市场信用违约事件频发的今天，CDS已经成为了银行信用风险转移的重要工具，但CDS对银行系统性风险影响的研究目前还没有统一的结论。因此，本文考虑到现实中银行、企业与CDS的交互作用，以及CDS对银行系统的双重影响，构建了一个动态的具有CDS的多重复杂银行网络模型。通过仿真分析了具有CDS的银行网络信用风险的演化机制，得到结论：1）与传统的银行系统相比，在经济稳定时期，CDS为银行提供了信用风险转移渠道，缓冲了银企间的信用风险，提高了银行系统的稳定性。2）CDS虽然可以减少银行的风险资产并提高盈利能力，但在经济波动时期银行系统也可能会面临承担更大的风险的可能。3）CDS的规模与银行系统性风险呈负相关关系，且规模存在临界值。在临界值内，随着CDS的规模的增加，银行系统性风险不断降低。但当CDS规模超出临界值时，银行系统性风险不会因CDS规模的变化而变化。

以上研究结果揭示了银行、企业以及CDS的复杂业务关联的微观基础，有利于从理论角度挖掘多重网络结构中各组织的内在联系，为监管部门从多重网络视角监控系统提供参考。另外，CDS对金融系统的影响远不及此，未来可能会着重研究中央监管机构对CDS的宏观调控政策。

参考文献：

[1]方意，赵胜民，黄丽灵，等.房地产市场与银行业系统性风险[J].管理科学学报，2024（11）：2643.

FANG Y， ZHAO S M， HUANG L L， et al. The real estate market and systemic risk in the banking system[J]. Journal of Management Sciences in China， 2024（11）：2643.

[2]LADLEY D. Contagion and risk-sharing on the inter-bank market[J]. Journal of Economic Dynamics and Control， 2013， 37（7）： 13841400.

[3]MITCHENER K J， RICHARDSON G. Network contagion and interbank amplification during the great depression[J]. Journal of Political Economy， 2019， 127（2）：465507.

[4]LEVENTIDES J， LOUKAKI K， PAPAVASSILOOU V G. Simulating financial contagion dynamics in random interbank networks[J]. Journal of Economic Behavior & Organization， 2019， 158： 500525.

[5]BARGIGLI L， GALLEGATI M， RICCETTI L， et al. Network analysis and calibration of the “leveraged network-based financial accelerator”[J]. Journal of Economic Behavior & Organization， 2014， 99： 109125.

[6]SILVA T C， ALEXANDRE M D S， TABAK B M. Bank lending and systemic risk： a financial-real sector network approach with feedback[J]. Journal of Financial Stability， 2018， 38： 98118.

[7]SHAN C， TANG D Y， YAN H， et al. Credit default swaps and bank regulatory capital[J]. Review of Finance， 202 25（1）： 121152.

[8]DANIS A， GAMBA A. The real effects of credit default swaps[J]. Journal of Financial Economics， 2018， 127（1）： 5176.

[9]陈庭强，周文静，童毛弟，等.融合CDS网络的银行间信用风险传染模型研究[J].中国管理科学，2020，28（6）：2437.

CHEN T Q， ZHOU W J， TONG M D， et al. Research on the model of interbank credit risk contagion by fusing CDS networks[J]. Chinese Journal of Management Science，2020，28（6）：2437.

[10] ALLEN F， CARLETTI E. Credit risk transfer and contagion[J]. Journal of Monetary Economics， 2006， 53（1）： 89111.

[11] WAGNER W， MARSH I W. Credit risk transfer and financial sector stability[J]. Journal of Financial Stability， 2006， 2（2）： 173193.

[12] D’ERRICO M， BATTISTON S， PELTONEN T， et al. How does risk flow in the credit default swap market？[J]. Journal of Financial Stability， 2018， 35： 5374.

[13] THORNTON J， DI TOMMASO C. Credit default swaps and regulatory capital relief： evidence from European banks[J]. Finance Research Letters， 2018， 26： 255260.

[14] Brunetti C， Harris J H， Mankad S， et al. Interconnectedness in the interbank market[J]. Journal of Financial Economics， 2019， 133（2）： 520538.

[15] AL-OWN B， MINHAT M， GAO S. Stock options and credit default swaps in risk management[J].Journal of International Financial Markets， Institutions， and Money， 2018，53（3）：200214.

[16] BO L， CAPPONI A. Counterparty risk for CDS： default clustering effects[J]. Journal of Banking & Finance， 2015， 52：2942.

[17] SCHULDENZUCKER S， SEUKEN S， BATTISTON S. Default ambiguity： credit default swaps create new systemic risks in financial networks[J]. Management Science， 2020， 66（5）： 19811998.

[18] CATULLO E， GALLEGATI M， PALESTRINI A. Towards a credit network based early warning indicator for crises[J]. Journal of Economic Dynamics and Control， 2015， 50： 7897.

[19] IORI G， JAFAREY S， PADILLA F G. Systemic risk on the interbank market[J]. Journal of Economic Behavior & Organization， 2006， 61（4）： 525542.

[20] GATTI D D， GALLEGATI M， GREENWALD B， et al. The financial accelerator in an evolving credit network[J]. Journal of Economic Dynamics and Control， 2010， 34（9）： 16271650.

[21] RICCETTI L，RUSSO A，GALLEGATI M. Leveraged network-based financial accelerator[J]. Journal of Economic Dynamics and Control， 2013， 37（8）： 16261640.

（责任编辑 耿金花）